架空输电线路覆冰不平衡张力影响因素研究
李攀峰 谢芳 俞永军
(1.国网绍兴供电公司,浙江 绍兴312000;2.绍兴文理学院,浙江 绍兴312000)
架空输电线路覆冰不平衡张力影响因素研究
李攀峰1谢芳2俞永军1
(1.国网绍兴供电公司,浙江绍兴312000;2.绍兴文理学院,浙江绍兴312000)
覆冰不平衡张力是导致直线塔倒塔和损坏的主要原因之一,如何提高杆塔抵抗覆冰不平衡张力的能力是设计人员必须关注的问题.结合架空输电线路的地形、覆冰特点,从耐张段的连续档数量、档距大小及不均匀性、挂点高差、断面模型、悬垂串等多方面,对影响覆冰不平衡张力的相关因素进行了详细的计算分析论证,结论用于指导杆塔排位优化,同时作为杆塔结构设计的依据之一,全面提高重覆冰区线路的抗冰能力.
覆冰;架空输电线路;不平衡张力;影响因素
在输电线路架线安装时,一般要求每个耐张档内各直线塔两侧的应力相等,直线塔悬垂串处于悬垂状态.但当运行工况发生变化时,因档距不均匀性、高差、不均匀覆冰等会造成直线塔两侧荷载不均匀,使直线塔两侧出现不平衡张力,从而造成悬垂串倾斜或导线滑动[1],尤其在不均匀覆冰的工况下,实际出现的直线塔覆冰不平衡张力可能大于标准的规定值,极易引起杆塔出现倒塔和损害事故.根据2008年冰灾引起的倒塔原因分析[2],覆冰不平衡张力是引起线路倒塔和断线的主要原因,本文推导出杆塔覆冰不平衡张力的计算方法,然后分析各种因素对杆塔覆冰不平衡张力的影响,
1 覆冰不平衡张力的计算方法
由于实际线路的杆塔位置千变万化,不均匀覆冰程度各不相同,实际出现的覆冰不平衡张力可能大于标准的规定值,造成对塔身稳定的破坏[3].因此,在线路杆塔定位设计中,可以通过逐基计算杆塔不平衡张力的方法,针对大档距、大高差、大小档等微地形采取杆塔加强及改进措施[4-6].覆冰不平衡张力计算方法如下.
1.1施工放线时连续档各档电线长度
连续档布置如图1所示,在施工安装电线时,要求各悬垂绝缘子串均调整为中垂位置,保持连续档内各档电线的水平应力相同[7],各档线长为:
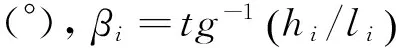
(1)

图1 连续档立面布置示意图
(2)
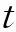
1.3正常运行时连续档各档变化档距
(3)
式(3)中ri为运行时电线比载N/m.mm2.
1.4正常运行时连续档各档档距增量
Δli=lni-li(m).
1.5正常运行时各悬垂绝缘子串偏移
连续档有N个档距和N+1基杆塔,设第1基的绝缘子串偏移为零,则第2基悬垂串水平偏移为δ2=Δl1,第3基为δ3=δ2+Δl2,第i基为:δi+1=δi+Δli(m).
1.6正常运行时连续档各档电线应力
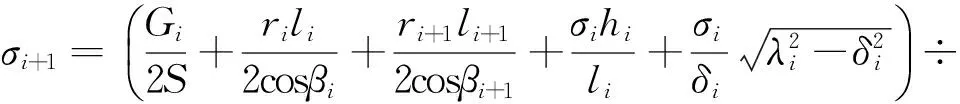
(4)

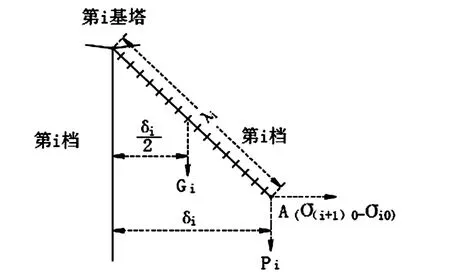
图2 悬垂串偏移示意图
对于整个耐张段,各档档距增量之和应为零,即第n基杆塔(耐张杆塔)上导线悬挂点的偏距应为零,采用计算机编程计算,收敛条件为:
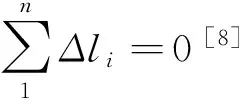
2 覆冰不平衡张力的取值
根据2008年我国南方大部分省份输电线路出现覆冰倒塔的情况分析,倒塔事故点多发生在大高差、大档距、大小档的地段.这些地段容易引起各档导线的水平应力不等,使直线杆塔上出现不平衡张力.在杆塔两侧覆冰不均匀时,这些地段的不平衡张力甚至可能超过杆塔的承受能力而发生倒塔事故.按《重覆冰架空输电线路设计技术规程》DL/T5440—2009[9],各种冰区的覆冰不平衡张力规定如下(见表1):
表1各种冰区覆冰不平衡张力取值表

冰 区覆冰不平衡张力(最大使用张力的百分数)悬垂型杆塔耐张型杆塔导 线地 线导 线地 线15mm中冰区1525354520mm中冰区2030405020mm重冰区2546425430mm重冰区29504658
3 各类影响不平衡张力的因素分析
结合架空线路耐张段的长度、连续档数量、挂点高差、地形因素等,着重对影响覆冰不平衡张力的相关因素进行计算分析.本文计算分析的基本条件为:导线型号JLHA1/G1A-300/50,导线设计覆冰取V=15m/s,C=20mm.
3.1档内不均匀覆冰组合工况的影响
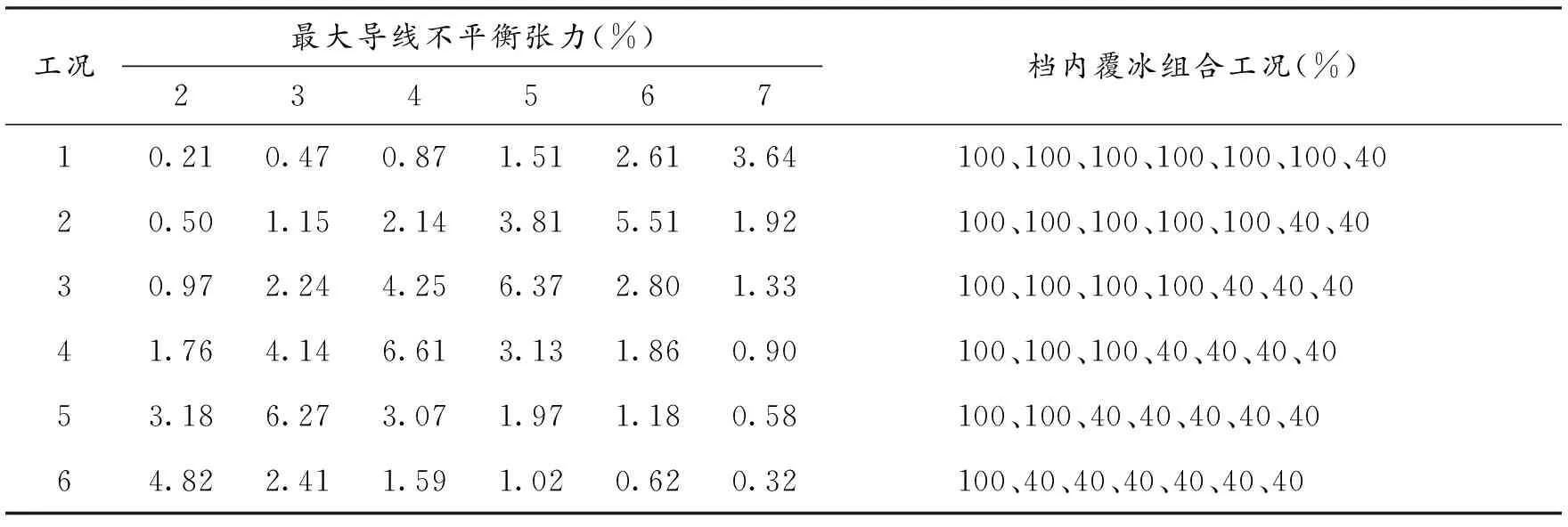
对于覆冰不平衡张力计算,规程只规定了待校验悬垂塔的两侧档内的覆冰率,对于耐张段内其他档的覆冰情况没有明确,故在一个连续档内因覆冰率不同而存在多种覆冰工况组合,以无高差等档距350m的7档模型进行各工况的遍历计算,其结果见表2.
反复计算其他档距下的等档距模型,可发现以下规律:对于等档距无高差模型,每种工况下的最大导线不平衡张力都是发生一侧所有档覆冰100%,另一侧所有档为不均匀覆冰的悬垂塔,且不平衡张力向该直线塔两侧衰减.而所有工况中最大导线不平衡张力发生在连续档中间档两侧直线塔,或连续档中间塔.
表27档模型、不同档内覆冰组合工况的直线塔不平衡张力计算表
工况最大导线不平衡张力(%)234567档内覆冰组合工况(%)10.210.470.871.512.613.64100、100、100、100、100、100、4020.501.152.143.815.511.92100、100、100、100、100、40、4030.972.244.256.372.801.33100、100、100、100、40、40、4041.764.146.613.131.860.90100、100、100、40、40、40、4053.186.273.071.971.180.58100、100、40、40、40、40、4064.822.411.591.020.620.32100、40、40、40、40、40、40
注:1.1#,8#为耐张塔,2#-7#为直线塔,“40”指40%覆冰,“100”指100%覆冰.
2.计算结果为各工况下每种覆冰组合中出现最大不平衡张力时,各档的不平衡张力.

图3 7档模型、不同档内覆冰组合工况时的
3.2档距大小、连续档数量的影响
按连续档数量为2档至10档、每档档距为300m至500m,组合后分别进行导线不平衡张力的计算,计算结果见表3和图4.
表3不同连续档数量、档距下的不平衡张力计算表
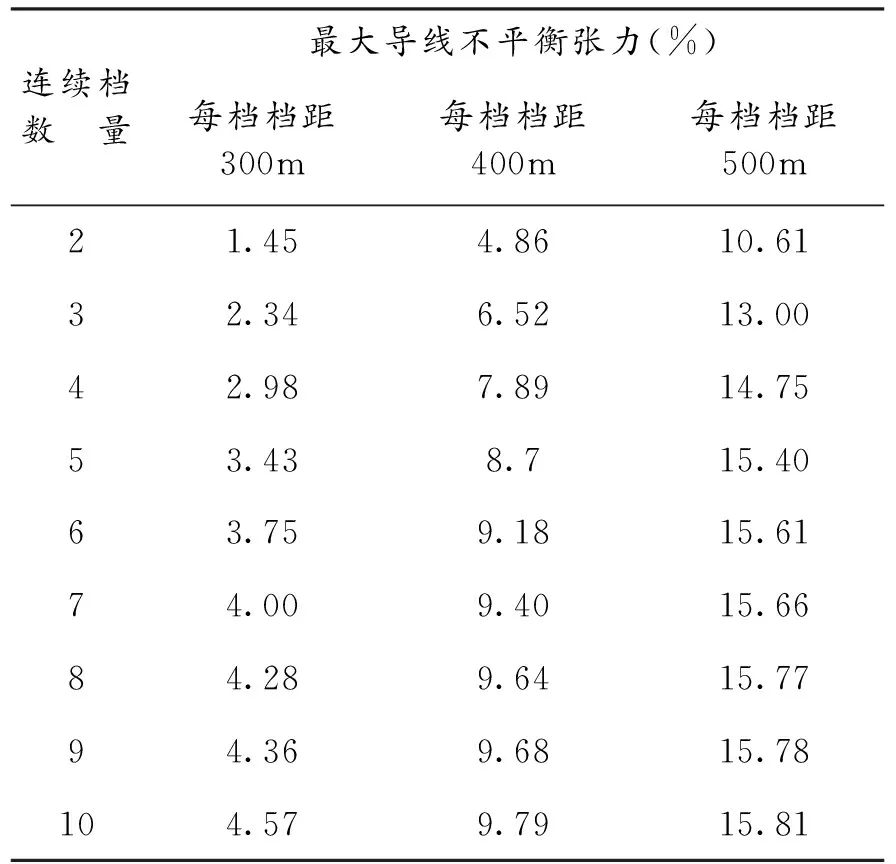
连续档数 量最大导线不平衡张力(%)每档档距300m每档档距400m每档档距500m21.454.8610.6132.346.5213.0042.987.8914.7553.438.715.4063.759.1815.6174.009.4015.6684.289.6415.7794.369.6815.78104.579.7915.81
从上列图表中可以看出,在连续档数不变的情况下,随着档距的增大,导线不平衡张力增长较快,500 m档距的不平衡张力比300 m时大2.5~6.3倍.由此可见档距大小对导线不平衡张力的影响极大.因此避免大档距,是限制不均匀冰所产生的不平衡张力的有效手段.
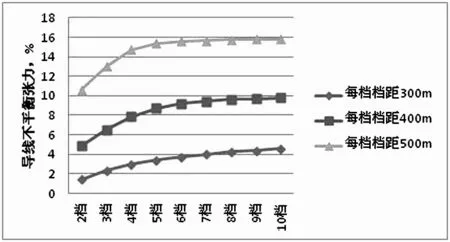
图4 不同连续档数量、档距下的不平衡张力
计算结果还表明,随着耐张段内连续档数量的增加,导线不平衡张力也随之增大,但很快便趋向饱和.如10档模型的导线不平衡张力比2档模型大3.0%~5.2%,但只比5档模型只大0.8%~1.4%.因此,在重冰区线路设计中,还可通过减少耐张段的连续档数量,来限制不均匀冰工况下的导线不平衡张力.另外也说明,对于分析导线最大不平衡张力,采用5档以上的连续档模型是可靠的.
3.3高差系数、断面模型的影响
根据前述分析,采用7档模型已能体现不均匀冰的最大不平衡张力.故采用7档-等档距400m模型,来计算分析高差系数对覆冰不平衡张力的影响,高差系数取5%~25%.
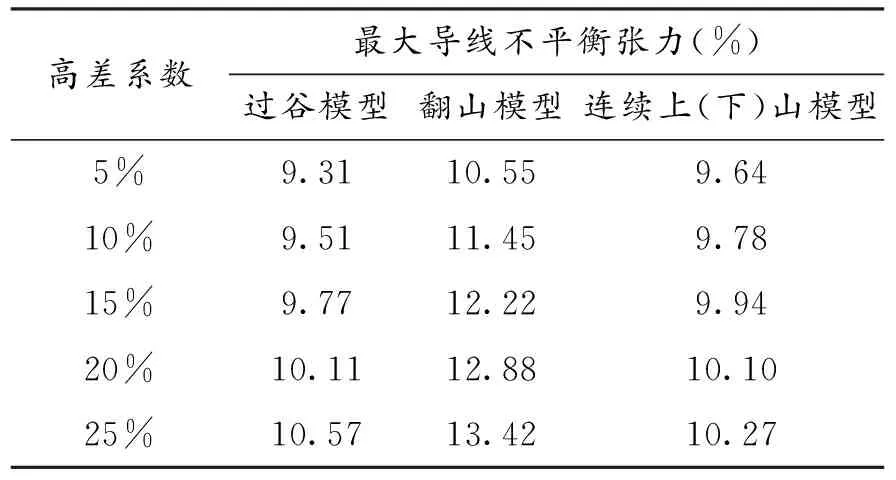
此外,考虑地形起伏因素,选用了山区线路三种典型断面模型(见图5):过谷模型、翻山模型、连续上下山模型,来综合分析断面模型的影响.计算结果见表4和图6.

A.过谷模型B.翻山模型
C.连续上(下)山模型
图5断面模型示意图
表4不同高差系数、断面模型的不平衡张力计算表
高差系数最大导线不平衡张力(%)过谷模型翻山模型连续上(下)山模型5%9.3110.559.6410%9.5111.459.7815%9.7712.229.9420%10.1112.8810.1025%10.5713.4210.27

图6 不同断面模型、不同高差系数的不平衡张力
在重冰区,不论哪种断面模型,其覆冰不平衡张力都随高差系数基本呈线性增大的,其中翻山模型对高差系数更为敏感、增幅最大,其次是过谷模型、连续上(下)山模型,但连续上(下)山模型的不平衡张力数值在5%~20%的高差范围内要大于过谷模型.
根据计算,翻山模型中发生最大不平衡张力的,是位于耐张段中间、山顶处的塔;连续上(下)山模型中发生最大不平衡张力的,是位于耐张段中间、半山腰处的塔.过谷模型中发生最大不平衡张力的,是位于山坡上、与耐张塔相隔一基的塔.
以上可以看出,覆冰不平衡张力是随着高差的增大而增大,并呈线性相关.断面为翻山模型时,覆冰不平衡张力是最严重的.
3.4档距不均匀的影响
考虑山区地形起伏,线路的实际排杆档距不可能非常均匀.故采用如图7所示的7档-20%高差-翻山模型,来分析在不均匀的档距分布下,对覆冰不平衡张力的影响.
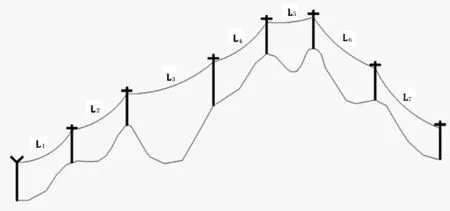
图7 不均匀档的计算模型
首先按L4为大档距,L1-L7为固定档进行分析,计算成果见表5:
表5不同变化档档距的不平衡张力计算表

L4档距(m)固定档档距200m固定档档距300m固定档档距400m最大导线不平衡张力(%)2003.24\3006.247.4440011.1011.5212.9750016.7116.5717.2760021.4621.5821.9870024.8425.7526.1880027.2228.8929.5490028.9831.1832.05100030.3732.8633.87
可见,在三个固定档档距中,随着大档距的增大,不平衡张力都是显著增加的,并基本呈线性相关趋势,故控制大档距是限制不平衡张力的有效措施.
3.5悬垂串的影响
当直线塔两侧出现不平衡张力时,悬垂绝缘子串会向张力大的一侧倾斜,张力大的一侧档距变小,张力随之减小,而另一侧张力增大,使直线塔所受的不平衡张力减小(见表6和图8).故本专题在翻山模型中采用不同的悬垂串串长,来分析其对不平衡张力的影响.
表6不同悬垂串串长时不平衡张力计算表
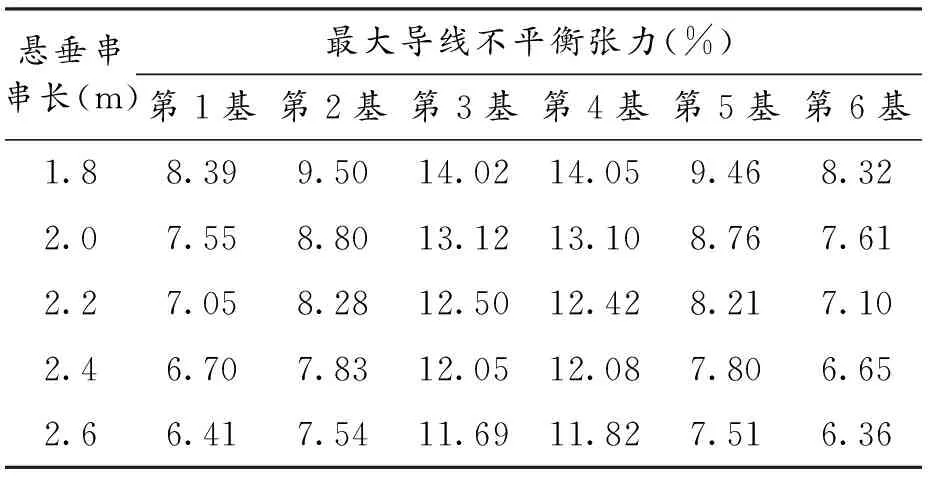
悬垂串串长(m)最大导线不平衡张力(%)第1基第2基第3基第4基第5基第6基1.88.399.5014.0214.059.468.322.07.558.8013.1213.108.767.612.27.058.2812.5012.428.217.102.46.707.8312.0512.087.806.652.66.417.5411.6911.827.516.36

图8 不同悬垂串串长的不平衡张力
根据计算结果可以看出,连续档内六基直线塔不平衡张力都是随着悬垂串串长的增加而减小的,对于同一基塔,2.2m的悬垂串的不平衡张力比1.8m的悬垂串的下降了2%~2.5%,但当串长增加到2.4m以上时,不平衡张力减少幅度已经非常小,同时必须增加塔头尺寸来满足电气距离要求.
4 结论
综合以上不均匀覆冰时导线不平衡张力的影响因数的研究,可以得出如下结论:
(1)连续档中每基直线塔的发生最大导线不平衡张力的工况均为:一侧所有档覆冰100%,另一侧所有档为不均匀覆冰时.
(2)连续档档数越多,直线塔不平衡张力越大,但当档数增加到5档以上时,不平衡张力增加趋近饱和,控制连续档数量可以减少不平衡张力.
(3)随着档距的增大,覆冰不平衡张力显著增大,故排杆时控制过大档距是减小不平衡张力的有效措施.
(4)当塔位之间高增大时,覆冰不平衡张力也随之增大,但增速十分缓慢.在同一高差系数的三种模型中,翻山模型断面的覆冰不平衡张力最大,尤其是大档距出现在山顶的情况下,位于山顶处的铁塔不平衡张力最大,排杆时应考虑采用加强型杆塔.
根据上述分析结论,可以有针对性地对连续档中不平衡张力较大的杆塔进行加强,或采用耐张塔开断连续档,从而充分限制整个输电线路的不平衡张力,提高线路的抗冰能力.
[1]卢本初,程思勇,何民.纵向不平衡张力计算与分析[J].广西电力,2009,32(6):89-92.
[2]陆佳政,蒋正龙,雷红才,等.湖南电网2008年冰灾事故分析[J].电力系统自动化,2008,32(11):16-19.
[3]张子引,刘学军.架空输电线路连续档不平衡张力计算[J].电力建设,2009,30(5):32-34.
[4]王守礼.影响电线覆冰因素的研究与分析[J].电网技术,1994(4):18-24.
[5]程思勇,薛志方.覆冰不平衡张力计算分析[J].电网与清洁能源,2011,27(2):10-13.
[6]史巍,黎燕霞,孙自堂.中、重冰区直线杆塔静态不平衡张力分析[J].华中电力,2011,24(2):6-9.
[7]国电公司.电力工程高压送电线路设计手册[M].北京:中国电力出版社,2003.
[8]孟遂民.架空输电线路设计[M].北京:中国电力出版社,2015.
[9]国家能源局发布.DL/T5440-2009重覆冰架空输电线路设计技术规程[M].北京:中国电力出版社,2012.
[10]中华人民共和国住房和城乡建设部.GB50545-2010110kV~750kV架空输电线路设计规范[S].北京:中国计划出版社,2010.
(责任编辑王海雷)
Affecting Factors of Icing Unbalance Tension of Overhead Transmission Lines
Li Panfeng1Xie Fang2Yu Yongjun1
(1. Shaoxing Power Supply Company, State Grid, Shaoxing, Zhejiang 312000;2. Shaoxing University, Shaoxing, Zhejiang 312000)
Icing unbalance tension, one of the main causes of collapse and damage of towers, is of main concern to designers to find ways to improve the ability of combating the icing unbalance tension. Combined with the topography, ice coating characteristics of overhead transmission lines, and from the perspectives of the number of spans in the tension segments, the length and non-uniformity of spans, the hanging point elevation, the section model, the suspension insulator, the paper conducts a detailed analysis and verification of the relative factors in this regard. The conclusion can be used to guide the tower arranging optimization, and used as one of the tower structure design basis, thereby improving the ability of transmission lines to resist ice coating in heavy icing areas.
ice coating; overhead transmission line; unbalance tension; affecting factor
2016-04-12
李攀峰(1983-),男,湖北天门人,注册电气工程师,主要研究方向为线路及杆塔、输配电技术理论与分析.
10.16169/j.issn.1008-293x.k.2016.08.19
TM753
A
1008-293X(2016)08-0107-06

