解题利器——根与系数的关系

王爱玲

解题利器
——根与系数的关系

王爱玲

在苏科版《数学》九年级上册第1章第3节有一个选学内容——一元二次方程的根与系数的关系，如果能掌握这个知识点，对于我们的解题将非常有帮助.

一、根与系数关系的推导

对于一元二次方程ax2+bx+c=0（a≠0）来说，如果b2-4ac≥0，那么它的两个根分别为

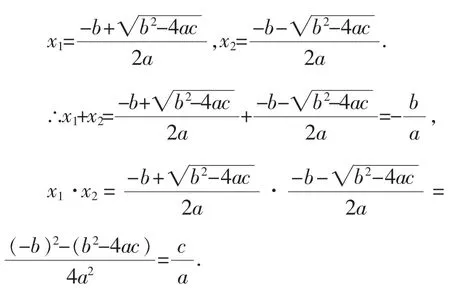
而在实际解题过程中，一元二次方程的二次项系数通常为1，那么这一关系可简化为：

如果x2+px+q=0的两根分别是x1和x2，则x1+ x2=-p，x1x2=q.

二、根与系数关系——解题利器

根与系数关系是由求根公式推导得到的，是求根公式应用的“升华”，它使用起来就应该更便捷.下面我们通过几道题目来谈谈根与系数关系在解题中的应用.

应用1一元二次方程两根的检验

例1已知一元二次方程x2+2x-7=0，则这个方程的两个根是（）.

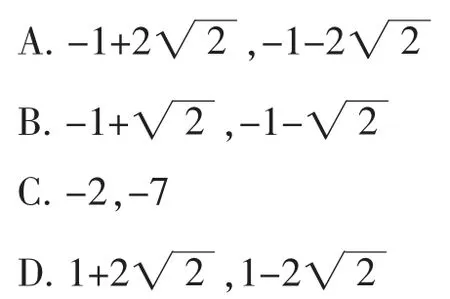
【分析】如果求解一元二次方程x2+2x-7=0，需要用公式法，比较麻烦，但如果用根与系数关系来判断可以迅速找到正确的选项，x1+x2=-2，x1x2=-7.

答案：A.

【方法点拨】由于这是一道选择题，因此只需找到正确的答案即可，如果解一元二次方程比较繁琐，可以采取其它一些“投机取巧”的方法来求解，如本题应用根与系数关系来判断.

应用2已知方程一根，可求另一根

例2已知方程5x2+kx-6=0的一个根为2，求它的另一个根及k的值.

【分析】方程5x2+kx-6=0已知二次项系数和常数项，所以x1x2的值已知，可根据两根之积先求出方程另一个根，然后根据两根之和求出k的值.

解：设方程的另一个根是x1，那么2

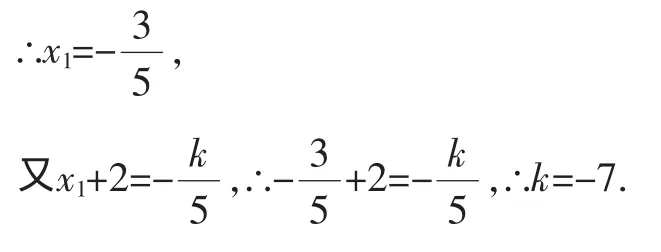
【方法点拨】当一元二次方程已知二次项系数和常数项时，相当于已知方程两根之积；当已知二次项系数和一次项系数时，相当于已知方程两根之和.当已知方程一根的时候，就很容易根据根与系数关系得到方程另一根.

应用3已知系数，求对称代数式的值

例3若x1、x2是一元二次方程x2-7x+5=0的两根，则的值是（）.

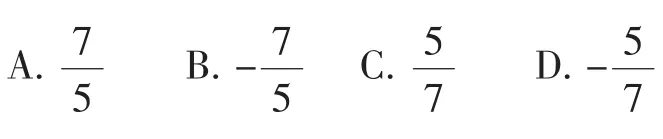
【分析】∵x2-7x+5=0，∴x1+x2=7，x1x2=5，

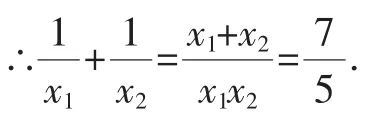
答案：A.

应用4逆用根与系数关系构造方程解决问题

例4已知两个数的和等于8，积等于7，求这两个数.

【分析】可以将这两个数看作是一个一元二次方程的两根，那么x1+x2=8，x1x2=7，代入x2-（x1+ x2）x+x1x2=0中，即可构造出两根分别为x1和x2的一元二次方程.

解：根据根与系数的关系可知，这两个数是方程x2-8x+7=0的两个根，

解这个方程，得x1=1，x2=7.

因此，这两个数是1，7.

【方法点拨】由于方程（x-x1）（x-x2）=0可化为x2-（x1+x2）x+x1x2=0，如果已知两根之和和两根之积，可根据这一性质构造出一个符合要求的一元二次方程.

例5已知x1，x2是方程x2+3x-5=0的两根，求以（x1+1）和（x2+1）为根的一元二次方程.

【分析】逆用一元二次方程根与系数的关系，但要注意新方程的两个实数根是（x1+1）和（x2+ 1），而不是x1，x2.

解：∵x1，x2是方程x2+3x-5=0的两根，

∴x1+x2=-3，x1·x2=-5，

∴（x1+1）+（x2+1）=x1+x2+2=-3+2=-1，

（x1+1）（x2+1）=x1x2+（x1+x2）+1=-5-3+1=-7，

∴以（x1+1）和（x2+1）为根的一元二次方程为：y2+y-7=0.

【方法点拨】已知一个一元二次方程，求新的一元二次方程，使它的根与原方程的根符合某种关系，这类题目的解题步骤是：①设出已知方程的两根，并依据所知关系写出所求方程的两根；②由根与系数的关系写出所设两根的和与积；③求新方程两根的和与积；④写出新方程.

应用5应用根与系数关系讨论方程根的情况

例6已知方程x2-4x-2m+8=0的两个根中一个大于1，另一个小于1，求m的取值范围.

【分析】由于这两个根一个大于1，另一个小于1，当这两根同时减去1，得到的两数必然一正一负，它们的乘积是负数，可根据这一条件列出关于m的取值范围.

解：方程有两个根，所以Δ＞0，

即42-4（-2m+8）＞0，

解得m＞2，同时根据根与系数关系可知：x1+x2=4，x1x2=-2m+8，由于两个根中一个大于1，另一个小于1，∴（x1-1）（x2-1）<0，

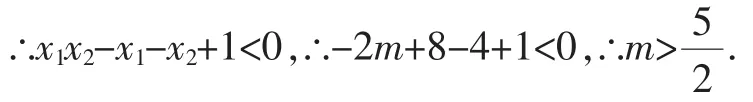
【方法点拨】本题已知的是两根之间的关系，要求的还是系数的取值范围，解决此类问题最终还是转化为一元二次方程根与系数的关系.

三、注意公式应用条件

一元二次方程根与系数关系的应用必须满足两个前提条件，首先这个方程必须是一元二次方程，一般表现为二次项系数不能等于0，其次这个一元二次方程要有两根，即保证根的判别式的值为非负数.

例7关于x的一元二次方程x2-3x+k+1=0的两根的平方和小于5，求k的取值范围.

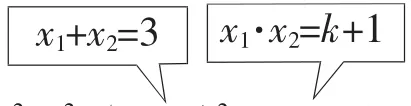
【分析】

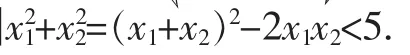
解：设方程两根分别为x1，x2，

又∵Δ=（-3）2-4（k+1）≥0，

【方法点拨】已知方程两根关系，探求字母系数的取值范围，可先将两根关系转化为两根之和和两根之积的形式，构造方程或不等式，确定字母的取值范围，务必要注意Δ≥0这个隐含条件.

（作者单位：江苏省海安县仇湖初中）