语义悖论、直观悖论和决策悖论——关于悖论的分类和解决

陈晓平

(华南师范大学 公共管理学院，广州　510006)



语义悖论、直观悖论和决策悖论
——关于悖论的分类和解决

陈晓平

(华南师范大学 公共管理学院，广州510006)

语义悖论有广义和狭义之分，广义的语义悖论包括所有悖论，而狭义的语义悖论与直观悖论和决策悖论相区别。直观悖论涉及语义分析与直观事实之间的背离，其中又有简单和复杂之分。简单的直观悖论包括芝诺悖论，复杂的直观悖论涉及对“直观事实”的解释或认识，就是所谓的“认知悖论”，如意外考试悖论。决策悖论是语义分析之结果的应用困境，它的产生常常不仅来自语义分析，而且来自价值分析，如囚徒困境。一些最简单的决策悖论只涉及操作而不直接涉及价值，故而称之为“操作悖论”，如理发师悖论。对这些不同类型的悖论分别给出解决方案，并以双信封悖论为例来说明有些悖论不只一种解决方案。

语义悖论；直观悖论；决策悖论；认知悖论；操作悖论

operation

悖论分为不同的类型，相应地，对悖论的解决也有不同的方法或途径。如何对悖论进行分类，对不同的悖论如何给以不同的解决？这些问题在学界是有许多争议的[1-2]。本文试图对这些问题给予一定的回答。

一、关于“悖论”的界定和分类

语义悖论和直观悖论是两种最为基本的悖论。语义悖论得自于两个相反命题(相互否定的命题)之间的逻辑互推，直观悖论是语义上得到推理支持的命题与直观“事实”之间的矛盾。二者的共同点是以逻辑推理为要素，而不仅仅是对客观事态的直接描述。对客观事态的直接描述属于对象语言；与之不同，以逻辑推理为要素并且关注逻辑推理本身及其结果，而不是关注它所涉及的客观事态，这样的论述属于元语言(至少相对于直接描述客观事态的对象语言是如此)。相应地，关于事态描述的矛盾命题属于对象语言中的逻辑矛盾，如“日本在亚洲并且日本不在亚洲”；基于逻辑推导并且关注点在推导本身的矛盾命题属于元语言中的逻辑矛盾，语义悖论和直观悖论均属此类。

以上论述涉及“矛盾”与“悖论”的区别。“矛盾”与“悖论”这两个词分别有广义和狭义之分。就广义的用法而言，它们之间没有区别，都指逻辑矛盾；但就狭义的用法而言，“矛盾”是指对象语言中的逻辑矛盾，即关于对象描述的矛盾命题，而“悖论”则是指元语言中主要涉及推理的矛盾命题[3]。我们这里采纳的是“矛盾”和“悖论”的狭义用法，以便更为集中地讨论狭义悖论所特有的性质和问题。为行文方便，以下所说“悖论”均指狭义悖论，除非有特别的申明。

在对“矛盾”和“悖论”做了以上区分之后，我们可以说：矛盾命题是假的，而悖论命题不仅是假的，甚至是无意义的。这是因为，后者不仅涉及事实，更重要的是涉及包含语义的推理。悖论的无意义的性质较为明显地体现于互推悖论(即后面所说的“狭义的语义悖论”)，因为这种悖论的着眼点是从一个命题的真推出它的假，又从它的假推出它的真，因此不宜把它简单地归结为假命题(或者说，这种悖论是从一个命题推出它的否定命题，又从它的否定命题推出该命题)。

需强调，涉及悖论的语言是指包含具体语义的语言，而不是纯粹的符号系统；纯粹的符号系统绝对不允许出现逻辑矛盾，否则就没有资格叫做“符号系统”。与之不同，包含具体语义的语言具有某种实用的功能，它的生命力在于它的实用性；一旦出现逻辑矛盾，人们不会立刻把它抛弃，而是力图消除逻辑矛盾，以某种改进的方式把有关的语言系统保留下来。因此可以说，所有值得研究的悖论都是语义悖论；甚至可以说，“悖论”就是“语义悖论”的简称。

不过，语义悖论还可划分为不同的类型。有些悖论仅仅是语义分析的，不涉及直观或应用，不妨称之为“狭义的语义悖论”，以区别于包含所有悖论的“广义的语义悖论”；在明白这种区别的情况下，也可把“狭义的语义悖论”简称为“语义悖论”。例如，集合论悖论属于狭义的语义悖论，因为它只是根据素朴集合论关于“集合”的定义而逻辑地推导出来的，不涉及关于集合的直观和应用；说谎者悖论也是如此。

另有一些悖论不仅是语义分析的，而且涉及语义分析的结果与直观“事实”之间的背离，不妨称之为“直观悖论”。解决直观悖论的途径有3种：一是只需纠正或改进语义分析所涉及的概念，如芝诺悖论；二是只需纠正或改进对“事实”的直观看法，如双信封悖论；三是既需要修改语义分析的概念，又需要修改对事实的直观看法，如意外考试悖论。后两种途径都涉及对“事实”的认知问题，不妨称之为“认知悖论”。认知悖论隶属于直观悖论，可以说是较为复杂的直观悖论。

再有一些悖论不仅是语义分析的，而且包含对语义分析之结果的应用困境，不妨称之为“决策悖论”。一般情况下，决策悖论不仅依据语义标准，而且依据价值标准，相对复杂一些，如囚徒困境属于此类。但有些决策悖论不直接涉及价值标准，只涉及应用标准和语义标准，相对简单一些，不妨称之为“操作悖论”，如理发师悖论。操作悖论隶属于决策悖论，可以说是较为简单的决策悖论。

接下来，我们将结合具体案例来讨论不同类型的悖论及其解决。由于所有悖论都包含语义悖论的成分，所以我们对语义悖论的讨论贯穿在对其他悖论的讨论之中，不再另设专门的章节。在转入对狭义的悖论的具体讨论之前，我们有必要对狭义的矛盾再进行简要说明。

二、关于狭义的矛盾及其解决

上面提到，狭义的矛盾是指对象语言中的逻辑矛盾，即关于对象描述的矛盾命题，而不是两个命题之间的互推，或者语义分析与直观事实之间的背离。此类逻辑矛盾的一个典型案例就是关于“自相矛盾”的寓言故事。某人X宣称：他的矛可以戳穿任何盾，他的盾可以抵挡任何矛。这句话的虚假性在一个问题面前暴露无疑，即：用他的矛来戳他的盾将有何结果？这个逻辑矛盾不是得自两个相反命题的互推，也不是得自这两个相反命题与某个直观事实相违背，而是在于这两个描述客观事态的命题必有一假。对这个矛盾的解决就是把那两个矛盾命题的合取命题作为假命题予以摈弃，或者对表述它的对象语言加以修改；如把那两个命题改为：X的矛可以戳穿除他自己的盾以外的任何盾，X的盾可以抵挡除他自己的矛以外的任何矛。这个修改后的命题不必是假的。

关于狭义的逻辑矛盾的另一个著名例子是“上帝万能困境”。一个人提出这样一个问题：上帝能够创造一块连他自己都举不动的石头吗？无论对这个问题给予肯定或否定的回答，都意味着上帝不是万能的。请注意，这个困境不是两个相反命题之间的互推，而是两个命题之间的单向推导，即由“上帝是万能的”推出“上帝不是万能的”，但从后一命题推不出前一命题。相应地，上帝万能困境并不仅仅意味着这两个相反命题必有一假，而且确定无疑地表明其中一个命题即“上帝是万能的”是假的。对上帝万能困境的解决就是把“上帝是万能的”这一假命题予以摈弃，或者对表述它的对象语言加以修改；如对“万能”这个概念加以限制，从而把“上帝万能”的命题改为：上帝能够做到任何人或任何对象所能做到的一切事情。显然，这个修改后的命题不必是假的，尽管它也得不到经验的证实。

关于上帝万能困境，有人指出那个问题——上帝能够创造一块连他自己都举不动的石头吗？——是不合法的，因为它已经预设上帝不是万能的。然而问题在于，这个预设不是别人从外边强加的，而是“万能”这个概念固有的，因此不应指责那个问题不合法，而应指责“万能”这个概念不合法。为了避免“上帝不是万能的”预设，甚至有人提议把那个问题改为：上帝能够做到任何并非他不能做到的事情吗？对这个问题的回答无疑是肯定的。然而不幸的是，这个问题包含同语反复，不仅对于上帝可以得出肯定的回答，而且对任何人或任何对象都可得出肯定的回答。可见，这一解决方案是不成立的，因为其价值是微不足道的。

总之，狭义的矛盾不同于狭义的悖论：前者是对象语言中的逻辑困境，而后者是元语言中的逻辑困境；前者面临被作为假命题而被摈弃或修改的压力，后者面临被作为无意义命题而被摈弃或修改的压力；前者相对容易一些，后者相对复杂一些。诚然，容易和复杂是相对而言的，上面关于狭义矛盾的两个例子也都或多或少地包含一些推导，因而也都涉及元语言，只是比起其他狭义悖论，它们涉及的推导和元语言的成分相对少一些。这意味着，狭义矛盾和狭义悖论并非截然不同，两者之间有一定的模糊性。

如果说那个“自相矛盾”的寓言是比较典型的狭义的矛盾，那么“上帝万能困境”并不是典型的狭义的矛盾，它在某些语境下更接近我们所说的(狭义的)悖论。例如，在基督教语境下，这句话不被作为假命题而被摈弃，而是把相关的推理看作有问题的而被修正。一种最为合理的修正是把推理中所涉及的“万能”概念加以限制或说明，从而把“上帝是万能的”这句话保留下来。在这种情况下，“上帝是万能的”与其说是矛盾，不如说是悖论。

三、直观悖论：意外考试悖论和芝诺悖论

意外考试悖论(the surprise exam paradox)历史上有多个类似版本，如“突然演习悖论”“意外绞刑悖论”和“求婚者悖论”等。意外考试悖论由哲学家奥康纳(D.J.O’Connor)于1948年正式提出，并以“实用悖论”(pragmatic paradox)称谓之[4]。几年后，另一位哲学家蒯因(W.V.O.Quine)将此悖论从认知的角度重新提起[5]，引起热烈的讨论，从此意外考试悖论常常被作为认知悖论(epistemic paradoxes)。

关于意外考试悖论的文献已经有不少，但对它的解决仍然众说纷纭，莫衷一是。主流的解决方案是把意外考试悖论归于“认知悖论”，进而在“知道”或“相信”的符号化及其形式推导上大做文章，离人们的直觉相去甚远。在笔者看来，这种做法是走了弯路，甚至犯了方向性的错误。与之不同，本文首先把意外考试悖论归于“直观悖论”，从直观的层面寻找关于这些悖论的更为简捷的解决方案。

意外考试悖论是这样的：一位老师对学生宣布，在下周的5个工作日内要考试，但哪一天不确定；这位老师宣称，考试时间是不能被预测到的。

一位学生这样想：老师一定不会在下周五考试，因为如果前四天不考试的话，星期五考试就成为可预测的。如果星期五不考试，那么星期四也不会考试，因为如果前三天和星期五不考试，那么星期四考试就成为可预测的。以此类推，星期一也不会考试，因为如果后四天不考试，那么星期一考试就成为可预测的。这样，老师每一天都不会考试。然而，这又同老师关于下周内必有考试的承诺相违背。这意味着，老师在下周内必有考试的承诺和让考试日期不可预测的承诺之间是相矛盾的。这是意外考试悖论第一层涵义，属于语义悖论，因为此悖论只需语义分析便可得出。

这一语义悖论使得老师在下周内必有不可预测的考试之承诺成为无法兑现的，或者说，老师的这一承诺是假的。正当同学们认为“老师的承诺是假的”时，老师突然宣布明天(如周二)考试，并且实施了。这一事实表明老师的那个承诺不是假的，而真的，是可以实现的。这是意外考试悖论的第二层涵义，即语义分析的结论与直观事实之间的矛盾，属于直观悖论。可以看出，这一直观悖论是以语义悖论为基础的。

为了说明直观悖论与语义悖论之间的关系，我们不妨再举一个例子即芝诺悖论，此悖论是由古希腊的一位叫做“芝诺”的智者提出的。芝诺悖论有4个，其中之一是“飞矢不动”：一支离弦之箭在到达靶心之前要先经过发射点与靶心之间的中点C1，在到达C1之前要先经过发射点与C1之间的中点C2，以此类推。这样的中点有穷多个，而经过无穷多个空间点需要花费无穷多个瞬间，而无穷多个瞬间就是无穷长的时间，所以，那支箭到不了任何地点，只能在发射点原地不动。但是，这个结论与人们的直观事实是相违的，因而属于直观悖论。

芝诺悖论与意外考试悖论的不同之处在于，后者即意外考试悖论既包含狭义的语义悖论，又包含直观悖论，具有狭义语义悖论和直观悖论的双重性；相比之下，芝诺悖论简单一些，只包含直观悖论。当然，直观悖论包含语义分析，这是任何悖论都具备的要素，因此它也属于广义的语义悖论，但它不包含狭义的语义悖论。

像芝诺悖论这样的简单直观悖论是语义分析与直观实事之间的矛盾，对它的解决有两个途径：一是指出语义分析中存在的错误，另一是指出关于事实的直观理解中存在的错误，通过纠正这些错误而使悖论得以消除。对于芝诺的“飞矢不动”悖论而言，出错的地方显然不在对事实的直观理解，也就是说，飞矢在运动这是一个不可动摇的事实；因此，我们只能在语义分析的过程上寻找错误。

不少学者指出，错误出在时空的“连续性”概念上，那种连续性使得任何一段时间或空间都包含无数多个点；然而，量子力学的“波粒二象性”和“时空量子”概念表明，这种单纯的连续性时空概念是错误的。一旦我们把这种单纯的时空连续性概念摈弃掉，那么“飞矢不动”的直观悖论也就迎刃而解了，即飞矢的出发点和靶心之间的距离不可能无限地分割下去，因而关于飞矢运动的时空分析不会导致“飞矢不动”的结论。

与之相比，意外考试悖论要复杂一些，既包含语义分析的错误，又包含直观解释的错误；这些错误一旦被纠正，此悖论也将随之得以消除。

四、对意外考试悖论的解决

意外考试悖论的关键词是“意外”即“不可预测”，预测可分为准确预测和概率预测。我们先不考虑概率预测，如下周五考试的概率是1/5，只考虑准确预测如下周五肯定考试。此外，我们还可以从时间上把预测区分为在下周之前的预测和下周每一天之前的预测。我们先考虑前者即下周之前不可准确预测考试日期。对此，老师只要采用抓阄的方法来确定考试日期，便可完全地实现他的意外考试的承诺。即使抓阄结果是下周五考试，并且学生们在下周四晚上准确预测到明天考试，但这与下周之前不可准确预测的规定并不冲突。这样，意外考试悖论便被消解了。

我们这里讨论的意外考试悖论是把“意外”解释为“下周每一天之前都不可准确预测”，这便使悖论似乎不能通过抓阄的方法加以解决，因为有可能抓到下周五考试，那便使考试日期在周四晚上成为可以准确预测的了。由此推出，周四、周三、周二和周一都不能进行“不可准确预测的”考试，因而下周内不可能进行一次不可准确预测的考试。

然而，这个语义分析是有缺陷的，因为它只是简单地考虑“可准确预测”或“不可准确预测”，而忽略了它们的概率。事实上，在下周前四天进行考试都是不可准确预测的(例如老师定在周四考试，学生在周三晚上便不能准确预测是在周四还是在周五考试)，因而不可准确预测之考试的概率为4/5，只有下周五考试是可被准确预测的，因而可准确预测之考试的概率只是1/5。相比之下，后者属于小概率事件，因而可被忽略不计；这样，下周进行一次不可被准确预测之考试便在事实上成为可操作的了(即大概率事件)。

如果有人觉得忽略1/5的可能性有些草率，那我们可以把操作方法设计得更周密一些。例如，通过抓阄来决定下周哪一天考试，并且把抓阄分为两个阶段，而抓阄结果不让学生知道：如果抓到下周前四天考试，那就照办，即下周进行一次不可准确预测的考试；如果抓到下周五考试，那就进行第二次抓阄。第二次抓阄设计为：共有100个阄，其中99个为“考试”，其中一个为“不考试”；这样，即使抓到“考试”的阄，那也是一次不可被准确预测的考试，因为毕竟还有不进行这一考试(即抓到“不考试”的阄)的可能性。这使“下周内进行一次不可被准确预测的考试”的概率大幅度上升，而其否定命题的概率则大幅度下降，从1/5下降为：1/5×0.01=0.002。如果愿意，还可在第二个抓阄阶段把阄的数目增大，从而把该否定命题的概率降得更小，甚至任意小，致使人们有充分理由对之忽略不计；进而认为，下周内进行一次不可被准确预测之考试在事实上是可操作的，尽管在理论上存在微小的不可操作的可能性。这样，关于意外考试悖论的直观悖论就被消除了。

需要强调，以上解决方案包含两个步骤：首先，在语义分析上弥补原来的不足，即不仅考虑下周考试是否可被准确预测，而且考虑它们的概率；其次，对“直观”或“事实”给出一种理论解释，即把小概率事件忽略不计，而把大概率事件看作事实。对“直观”或“事实”的解释属于认知理论，在这个意义上，可以把意外考试悖论所涉及的比较复杂的直观悖论叫做“认知悖论”。相比之下，芝诺悖论所涉及的直观事实如飞矢运动是无可置疑的，不需要借助认知理论加以解释和改变，需要解释和改变的仅仅是与这一事实发生冲突的运动时空理论。因此，芝诺悖论一般不被归入认知悖论。

五、决策悖论的一个简单案例：理发师悖论

理发师悖论是由罗素继集合论悖论之后提出的另一个著名悖论，其内容是：S村的理发师X规定：X只给那些不给自己刮胡子的S村人刮胡子。现问：X应该给他自己刮胡子吗？若回答“应该”，那么X一旦执行便成为不应该的了；若回答“不应该”，那么X一旦执行便成为应该的了。可见，X的规定是自相矛盾因而不可执行的。

意外考试悖论和理发师悖论在其性质上似乎很接近，它们都兼具语义悖论和直观悖论的双重性。然而，稍加分析便可知道，理发师悖论包含语义悖论而不包含直观悖论。首先，无论理发师X是否给自己刮胡子，都不违反直观；其次，这个悖论仅仅是从X的那个规定推导出来的，而那个规定不是事实，而是某种命令或规范。

我们知道，命令或规范涉及执行它的行动或操作，在这个意义上理发师悖论属于决策悖论。决策论的基本原则是“最大期望效用原则”，但是理发师悖论却不直接涉及效用，只涉及操作，因而是一种最简单的决策悖论即操作悖论。可以说，理发师悖论具有语义悖论和操作悖论的双重性，不同于意外考试悖论所具有的语义悖论与直观悖论的双重性。下面，我们首先讨论如何从语义方面消除理发师悖论。

对于理发师悖论的消除，一种较为简单的方法是把X的那个规定限制为：除他本人以外，X只给那些不给自己刮胡子的S村人刮胡子。一种略为复杂的方法是把X的那个规定限制为：X只给那些过去从未给自己刮胡子的S村人刮胡子。按此规定，如果X过去给自己刮过胡子，那他现在不应该给自己刮胡子；如果X过去从未给自己刮胡子，那么他现在应该给自己刮胡子；并且只刮这一次，此后不再给自己刮胡子。这里也不存在悖论。

然而，如果把X的规定明确为：X只给那些此时此刻不给自己刮胡子的人刮胡子，悖论似乎出现了。对于这个悖论的消除，关键是要指出“此时此刻”这个概念是含糊不清的。严格地说，“此时此刻”是不能说的，一旦被说出，那便成为“过去的某一刻”；正因为此，“此时此刻”也是不可执行的。这个操作困境直接得自于语义悖论，而这个语义悖论得自于“此时此刻”这个概念的含糊性。一旦我们把“此时此刻”解释为“过去的某一刻”，语义悖论便不存在了，相应的操作困境也就随之消失了；这一点上面已经说明。

也许有人坚持说，即使说出的“此时此刻”实际上是“过去某一刻”，但是我们也可以不说出来，而只把“此时此刻”存乎一心，作为一种观念用以指导行动。对此，笔者的回答是：首先，这个不可说的“此时此刻”不会导致语义悖论，因为它不属于语义范围；其次，这个只能存乎一心的“此时此刻”使得理发师的规定也只能存乎一心，不仅不能说出，而且不能操作，因为一操作就成为过去的某一行动；这样一来，作为操作悖论的理发师悖论也不存在。

进而言之，即使作为操作悖论的理发师悖论在某种意义上是存在的，那也是可以解决的；因为“操作”是否定闭包的，即不操作也是一种操作。具体地说，理发师X的这一规定使他不能操作，其结果是X不给自己刮胡子，而不给自己刮胡子也是一种操作。这样，此操作悖论便得到一个确定的解答，即：X不给自己刮胡子。

需要指出，“操作”是否定闭包的，但“意义”不是否定闭包的，即“无意义”不是一种意义，确切地说，不是原来语言层次的一种意义*低层语言的某种“无意义”可以在高层语言中成为有意义的，因为“无意义”这个语词本身是有意义的。正因为此，“最大的集合”或“所有集合的集合”在数学中是无意义的，但在哲学中可以成为有意义的，也许就是哲学所说的“宇宙”或“道”；正可谓“道可道，非常道”。不过，这样的讨论已经超出逻辑学的范围，属于形而上学。。与之不同，操作闭包性却是同一层次的，即：操作和不操作都是经验层次的。正因为此，不操作可以作为操作悖论的一种解决，但无意义不可以作为语义悖论的一种解决*对于操作悖论的解决，这里所说的方案与笔者之前提出的解决方案(见文献[6])有所不同，此方案可以看作是对前一方案的纠正或改进。前一方案把意外考试悖论、求婚者悖论和双信封悖论看作二阶操作悖论，对它们的解决是“怎么做都行”。现在看来这个说法是欠妥的，“怎么做都行”是无意义的行为，正如“怎么说都行”是无意义的语言。本文只把“不操作”作为对操作悖论的解决，而不是“怎么做都行”。此外，前一方案把理发师悖论归入(狭义的)语义悖论，而不看作操作悖论，这也是不妥的。。对于语义悖论的解决只能通过对某些概念或事实的澄清或限制而摆脱，所摆脱的在很大程度上正是“无意义”的困境。

六、决策悖论的一个复杂案例：囚徒困境

囚徒困境是决策论中的一个著名案例，常常用来讨论道德问题。囚徒困境是这样的：彼此非常熟悉的两个罪犯A和B因共同作案而被分别关押在两间牢房里，他们两人都在思考明天受审时所应采取的策略：招供还是隐瞒？他们面临的效用矩阵是：

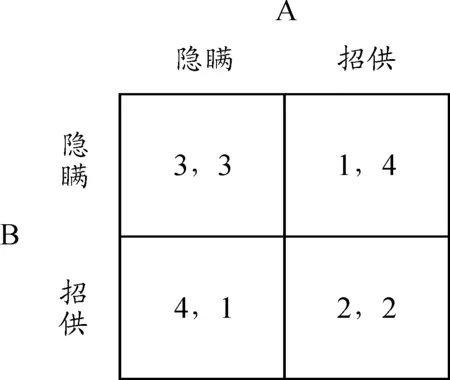
这个矩阵中有4对数字，每对数字中左边一个表示B的效用，右边一个表示A的效用。我们看到，在A隐瞒的情况下，B招供比隐瞒的效用要大，即4大于3；在A招供的情况下，也是B招供比隐瞒的效用要大，即2大于1。这表明，无论A隐瞒还是招供，B都应当招供。同样的分析也适用于A。这样，A和B都将选择招供，他们的效用均为2。但是，他们又一想，对方与自己的思维方式和道德倾向是十分接近的，两者都考虑到这种局面的形成并都想摆脱这种局面，即：与其两人都选择招供，还不如两人都选择隐瞒，因为这将使他们的效用均由2变为3。然而，再一想，如果自己隐瞒而对方却招供，自己会吃大亏，即处于1∶4的状况，因而还是选择招供为好。这样，两个囚徒又回到2∶2的局面，从而陷入举棋不定、左右为难的决策困境之中。

囚徒困境是关于隐瞒和招供的二难选择，可以推广到人们之间关于合作与对抗的二难选择，因而具有普遍的道德意义。对囚徒困境有不少解决方案被提出，其中重复博弈的解决方案最有影响。当博弈只进行一次时，每个参与者只关心一次性的效用；但是，如果博弈重复多次，参与者就可能为了长远利益而牺牲部分眼前利益。如果A和B之间的博弈长期多次进行，而且他们知道彼此都是理性的，着眼于长远个人利益的最大化，A和B将采取合作态度，即都选择隐瞒。因为彼此都清楚，一旦自己招供，对方就会在以后的博弈中也招供。虽然只就某一次博弈来说，他招供比隐瞒更有利，但从长远个人利益来看招供会使自己遭受更大的损失。于是两人采取合作的态度即都选择隐瞒，这样便跳出了“囚徒困境”。

然而，从道德哲学讲，这一模型所提供的方案是有缺陷的。因为对任何一个人来说，博弈不会无限次地进行下去，总会有一个终点，而重复博弈的最后一次博弈与一次性博弈所面临的难题并没有本质的区别；也就是说，重复博弈并没有从根本上消除囚徒困境，只是把这种困境后移了，理论上的问题依然存在。例如，一个人由于某种原因以后不再同别人打交道的时候(一个极端的例子是临死的那天)，他就有理由做一件只对自己有利而对他人或社会有害的事情，因为他与别人的重复博弈即将终止。

可见，重复博弈模型要想最终解决道德堕落的问题，就必须假定这个重复博弈是无限地进行下去的。然而，这一假定对于一个人来说是无用的，因为人生毕竟是有限的。所以，从道德哲学上讲，囚徒困境的解决最终依赖人们道德动机的改变，即从绝对利己主义转向相对利己主义；具体地说，从“以怨报德”或“损人利己”的行为动机转入“以怨报怨，以德报德”的行为动机。需指出，这并不意味着完全的利他主义是更为可取的道德动机，决策论的另一案例即“情侣困境”表明，完全的利他主义也会导致道德冲突。

通过以上对囚徒困境的分析我们看到，除操作悖论以外，一般的决策悖论不仅与语义分析有关，而且与包括道德动机在内的价值标准有关。相应地，对一般决策悖论的解决也有两个途径：一是从语义分析的角度澄清或改变某些概念，另一是对某些价值标准加以调整或改变；这是决策悖论不同于其他悖论之解决的一个关键之处。以上对于囚徒困境的解决最终依赖于对道德动机的调整或改变。

至此，我们结合具体案例对各种类型的悖论给以分析和解决。不过，以上讨论似乎给人留下一个印象，即每个悖论只有一种解决方案，其实不然。对此，我们以双信封悖论为例加以说明。

七、作为直观悖论的双信封悖论：两种解决方案

双信封悖论(the two envelopes paradox)早在20世纪初就被提出，直到现在仍被哲学家和经济学家们讨论[7]。双信封悖论是这样的：面对A和B两个信封，A内装有X元钱，B内装有Y元钱，并知其中一个信封内的钱是另一个的2倍，问你选哪个信封？

令E(X)和E(Y)分别为A、B两信封的期望值。由于信息均等，或者说由于信息的无差别性，故E(X)=E(Y)。于是，当面临A和B的选择时不应有倾向性，只应随机地选择其中一个。这里依据的就是所谓“无差别原则”(the Principle of Indifference)。然而，一旦你选择其中一个信封，则对另一个信封的期望值成为：

(1)选择A，对B的期望值是:E(Y)=1/2×X/2+1/2×2X= X 5/4

或者，

(2)选择B，对A的期望值是:E(X)=1/2×Y/2+1/2×2Y= Y 5/4

这样矛盾便出现了：无论你选择A或B，你总是倾向于换另一个信封，这与你开始时给A和B以相等的期望值是相违的。换言之，在对两个信封A和B信息均等的情况下，给二者赋予相同的期望值在直观上是合理的，但是以上理论分析所得出的结论是二者的期望值不相等；因此这是一个直观悖论。

前面谈到关于直观悖论的两种解决方案：一是维持直观不变，而对用以进行语义分析的概念加以澄清或限制；二是不仅改进语义分析，而且对直观给以适当的调整或限定。有些直观悖论适合于前一种解决方案，如芝诺悖论；另一些直观悖论适合于后一种解决方案，如在对意外考试悖论的解决中借助“大概率事件”来解释“事实”，并加以语义分析和推导方面的改进。其实，还有第三种方案，即维持语义分析不变，只对直观事实给以适当的调整或限定。下面讨论的双信封悖论则涉及第一种方案和第三种方案。

关于双信封悖论的第一种解决方案是对其发生条件加以限制，即把两个信封的金额总数固定下来*参阅文献[8]，但该文献并未把双信封悖论作为直观悖论来看待。；一旦把金额总数固定下来，悖论就不存在了。现假定两个信封的金额总数是S，平均分为3份，每份为S/3。相应地，对A信封和B信封的期望值均为：E(X)=E(Y)=1/2×2S/3+1/2×S/3= S/2。基于这一语义分析，两个信封的期望值是相等的，即各为金额总数的一半，符合人们对两个信封的直观期望值，所以双信封悖论并不存在。

关于双信封悖论的另一种解决方案是不对其发生条件加以限制，而是对两个信封的期望值相等这一直观加以调整，即由静态相等调整为动态相等。具体地说，对两个信封的金额总数不加限制，根据前面给出的公式(1)和(2)，你将回到“这山望见那山高”的局面，因而你将不停地交换信封。不过，这实际上是一种动态平衡，同样使得E(X)=E(Y)是成立的。于是，你将做出决定：随机地选择一个信封，并且不再交换。这一决定与我们的直觉——赋予两个信封以相等的期望值——是相符的，所以双信封悖论随之消失。

请注意，以上两种解决方案所针对的是两个不同的双信封悖论：前一个是对金额总数加以限制的，后一个是对金额总数不加限制的。两种方案的所得结果都符合我们对于两个信封有着相等期望值的直观，这使相应的两个直观悖论都得以消除。

[1]陈波.悖论研究[M].北京：北京大学出版社，2014.

[2]张建军.逻辑悖论研究引论[M].南京：南京大学出版社，2002.

[3]夏素敏.悖论的语用学概念及其方法论意义——兼评《逻辑悖论研究引论(修订版)》[J].重庆理工大学学报(社会科学)，2014(12)：5-10.

[4]O’CONNOR D J.Pragmatic paradoxes[J].Mind,1948，57:358-359.

[5]QUINE W V O.On a so-called paradox[J].Mind,1953，62:65-67.

[6]陈晓平.意外考试悖论及其解决——兼论求婚者悖论和双信封悖论[J].湖南科技大学学报(社会科学版)，2013(3)：25-30.

[7]罗伊·索伦森.悖论简史[M].贾红雨，译.北京：北京大学出版社，2007.

[8]GFFIN A.The error in the two envelopes paradox[EB/OL].[2016-01-06].http://wenku.baidu.com/view/8838eb4469eae009581bec3d.html.

(责任编辑张佑法)

Semantic Paradox, Intuitive Paradox and Decision Paradox:the Classification and Settlements of Paradoxes

CHEN Xiao-ping

(School of Public Administration, South China Normal University, Guangzhou 510006, China)

The concept of semantic paradox is to be understood in two sense: in the broad sense, semantic paradox contains all of the paradoxes; in the narrow sense, it is distinguished with intuitive paradox and decision paradox. Intuitive paradox, which involves deviation between semantic analysis and intuitive fact, could be divided into simple and complex one. Unlike Zeno paradox, which is the simple intuitive paradox, the complex intuitive paradox refers to the interpretation and recognition of the “intuitive fact”, so that it could be called “cognitive paradox”, e.g., the Surprise Exam paradox. Meanwhile, decision paradox comes from the application of semantic analysis, which is not only caused by the semantic analysis but also by value analysis. The simplest decision paradox refers to operation only, thus it can be called “paradox of operation”, e.g., the Barber paradox. This article has put forward some settlements for the different types of paradoxes, and, through an example of the Two Envelopes paradox, gives a demonstration that there are more than one solutions for some paradoxes.

semantic paradox; intuitive paradox; decision paradox; cognitive paradox; paradox of

2016-07-11

国家社会科学基金重大项目“现代归纳逻辑的新发展、理论前沿与应用研究”(15ZDB018)；国家社会科学基金重大项目“基于虚拟现实的实验研究对实验哲学的超越”(15ZDB016)

陈晓平(1952—)，男，山西昔阳人，教授，博士生导师，研究方向：科学哲学、分析哲学、道德哲学。

format：CHEN Xiao-ping.Semantic Paradox, Intuitive Paradox and Decision Paradox: the Classification and Settlements of Paradoxes[J].Journal of Chongqing University of Technology(Social Science)，2016(9):6-13.

10.3969/j.issn.1674-8425(s).2016.09.002

中国逻辑学会会长邹崇理 研究员

B81

A

1674-8425(2016)09-0006-08

引用格式：陈晓平.语义悖论、直观悖论和决策悖论——关于悖论的分类和解决[J].重庆理工大学学报(社会科学)，2016(9):6-13.

主持人语：

如何对悖论进行分类，如何对不同的悖论给出不同的解决方法？对此，学界见仁见智。陈晓平教授《语义悖论、直观悖论和决策悖论——关于悖论的分类和解决》一文对这些不同类型的悖论有独到的见解，分别给出解决方案，并以双信封悖论为例来说明有些悖论的解决方案是多种的。

证明网络是范畴语法分析自然语言的计算机实现的技术，证明网络对于理解范畴语法的计算性质具有重大价值。《证明网络与语言处理》一文概括了证明网络的大体内容及其在语言处理上的优势，属于逻辑学和计算机科学的交叉研究，值得关注。

在当前提倡批判性思维素质教育的背景下，《全球经济新常态下的领导与批判性思维》一文的选题较有特色。文章指出，现有或潜在的领导者在批判性思维方面的素养并不充分，亟待在有关的教育中予以加强。文章的论证较充分，具有一定的理论意义。