Box Dimension of Weyl Fractional Integral of Continuous Functions with Bounded Variation

Lei Mu，Kui Yao，∗，Yongshun Liangand Jun Wang

1Institute of Science，PLA University of Science and Technology，Nanjing，Jiangsu 211101，China

2Institute of Science，Nanjing University of Science and Technology，Nanjing，Jiangsu 210094，China



Box Dimension of Weyl Fractional Integral of Continuous Functions with Bounded Variation

Lei Mu1，Kui Yao1，∗，Yongshun Liang2and Jun Wang1

1Institute of Science，PLA University of Science and Technology，Nanjing，Jiangsu 211101，China

2Institute of Science，Nanjing University of Science and Technology，Nanjing，Jiangsu 210094，China

.We know that the Box dimension of f（x）∈C1［0，1］is 1.In this paper，we prove that the Box dimension of continuous functions with bounded variation is still 1.Furthermore，Box dimension of Weyl fractional integral of above function is also 1.

Fractional calculus，box dimension，bounded variation.

AMS Subject Classifications:28A80，26A33，26A30

1　Introduction

As a new branch in mathematics，fractal geometry has proved its value with many applications over many fields.Many initial and conclusive results on fractals were done in［2，3，7］.If f（x）has continuous derivative，it is not difficult to see that Box dimension of f（x）is 1，indeed a regular 1-set.We want to know whether this result still holds for the function f（x）with bounded variation？What about their fractional integral？Firstly，we give definitions of Hausdorff dimension and Box dimension.

Definition 1.1（see［1］）.Let a Borel set F∈Rnis as follows.For s≥0 and δ＞0，define

where|U|=sup｛|x-y|:x，y∈U｝denotes the diameter of a nonempty set U and the infimum is taken over all countable collections｛Ui｝of sets for which F⊂∪∞iUiand0＜|Ui|≤δ.As δ decreases，Hsδ（F）can not decrease，and therefore it has a limit（possibly infinite）as δ→0；define

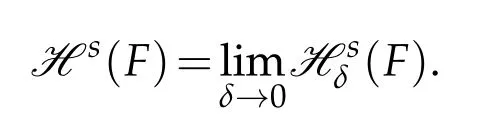
The quantity Hs（F）is known as s-dimensional Hausdorff measure of F.For a given F there is a value dimH（F）for which Hs（F）=∞for s＜dimH（F）and Hs（F）=0 for s＞dimH（F）.Hausdorff dimension dimH（F）is defined to be this value，that is:

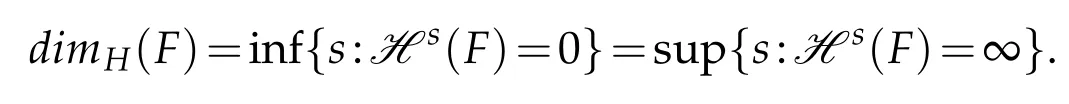
Definition 1.2（see［1］）.Let F be a any non-empty bounded subset of R2and let Nδ（F）be the smallest number of sets of diameter at most δ which can cover F.The lower and upper Box dimensions of F respectively are defined as

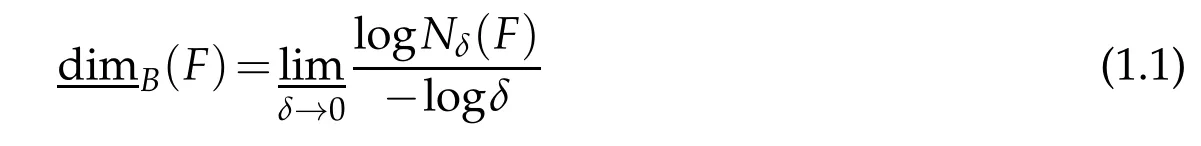
and

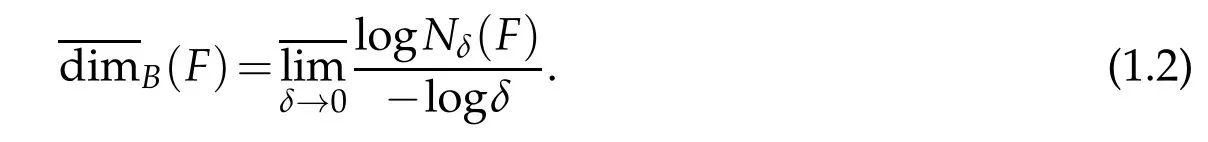
If（1.1）and（1.2）are equal，we refer to the common value as the Box dimension of F:

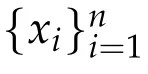
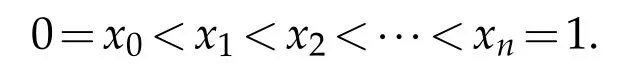
Write

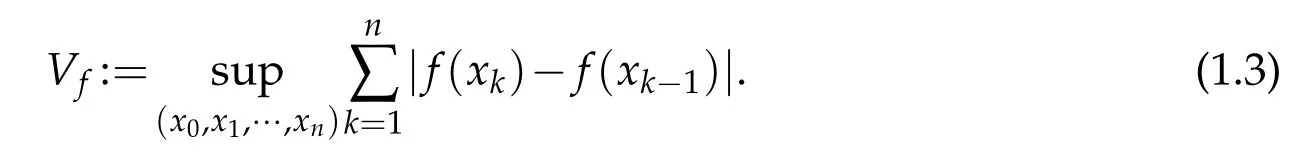
If（1.3）is finite，then f（x）is of bounded variation on I.Let BVIdenote the set of functions of bounded variation on I.Meanwhile，Let C（I）denote the set of functions which are continuous on I.

Definition 1.4（see［4］）.Let f（x）∈C（I）and 0＜v＜1.If f（x）is piecewise integrable，we define the Weyl fractional integral of f（x）of order v as

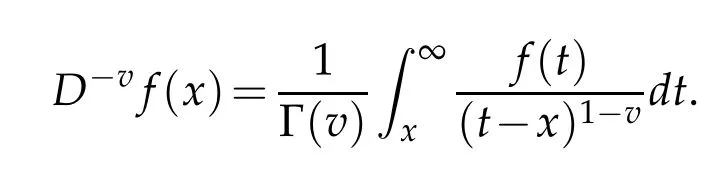
In this paper，let G（f，I）denote the graph of f（x）on I，and dimBG（f，I）denote the Box dimension of f（x）on I.

2Lemmas

We first derive some simple but widely applicable estimates for the Box dimension of graphs.Given a function f（x）and an interval［a，b］，we write Rfthe maximum range of f（x）over［a，b］，i.e.，

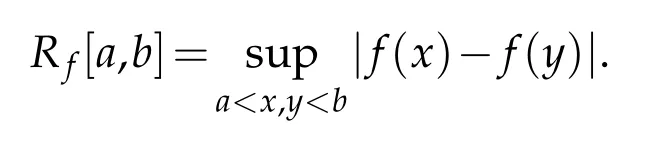
To prove theorems of Section 3，we need some lemmas.

Lemma 2.1（see［1］）.Let f（x）∈C（I）∩BVI.Suppose that 0＜δ＜1，and m be the least integer greater than or equal to δ-1then，if Nδis the number of squares of the δ-mesh that intersect G（f，I），then

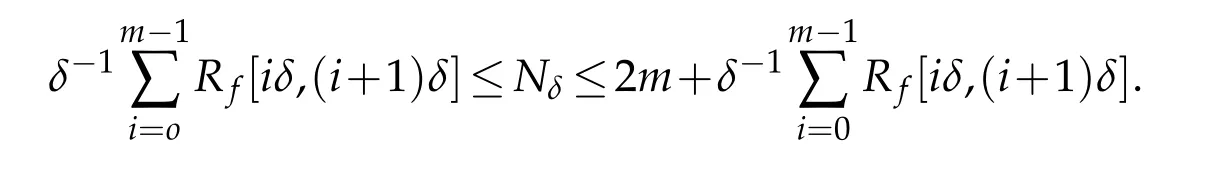
Proof.The number of mesh squares of side δ in the column above the interval［iδ，（i+1）δ］that intersect G（f，I）is at least Rf［iδ，（i+1）δ］/δ and at most 2+（Rf［iδ，（i+1）δ］/δ）.f（x）is continuous.By summing all such intervals together，we can get Lemma 2.1.

If f（x）is a continuous function and Box dimension of f（x）exists，we know that Box dimension of any continuous functions is no less than 1.Then we give the following lemmas.

Lemma 2.2.If f（x）is a continuous function on I，we have dimBG（f，I）≥1.

Proof.By using Definition 1.2，we have

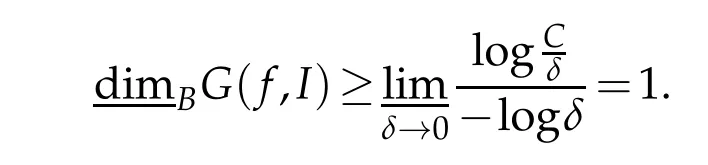
So we get the conclusion that dimBG（f，I）≥1.

Lemma 2.3.If f（x）is a continuous function on I，then dimBG（f，I）≤2.

Proof.By using Definition 1.2，we have

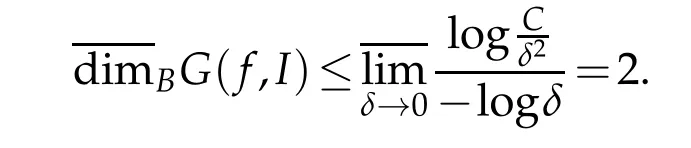
Then dimBG（f，I）≤2.

3　Theorems

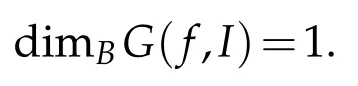
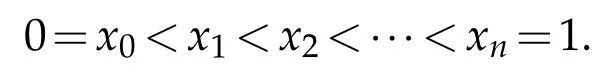
We have

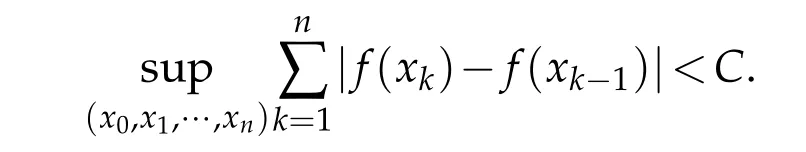
Let m be the least integer greater than or equal to 1/δ.Nδis the number of squares of the δ-mesh that intersect G（f，I）.By Lemma 2.1，we know

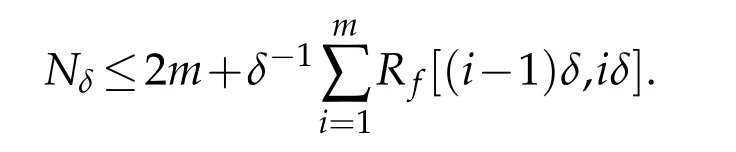
For 1≤i≤m-1 and xi，0=iδ，xi，3=（i+1）δ，xi，1，xi，2∈（iδ，（i+1）δ），

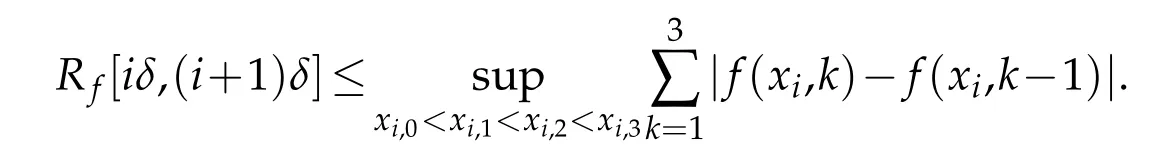
So there exists a certain absolutely positive constant C such that

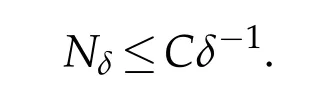
From Definition 1.1，it holds that

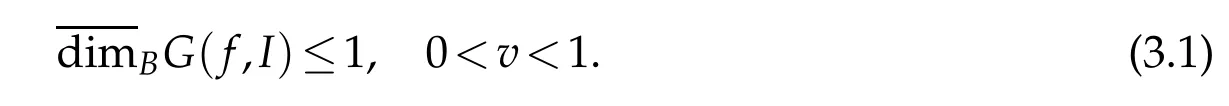
The topolopy dimension of a continuous function f（x）is no less than 1.From Definition 1.1，we get

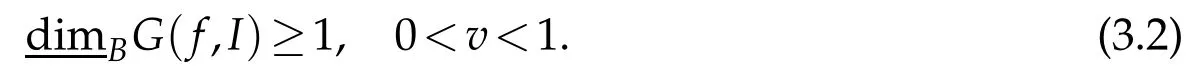
Combining（3.1）and（3.2），we get the result of Theorem 3.1.

Remark 3.1.If f（x）∈LipM，then dimBG（f，I）=1.

Proof.f（x）∈LipM，∀x，y∈I，we have

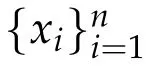
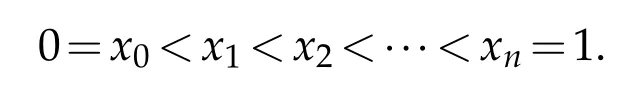
We have

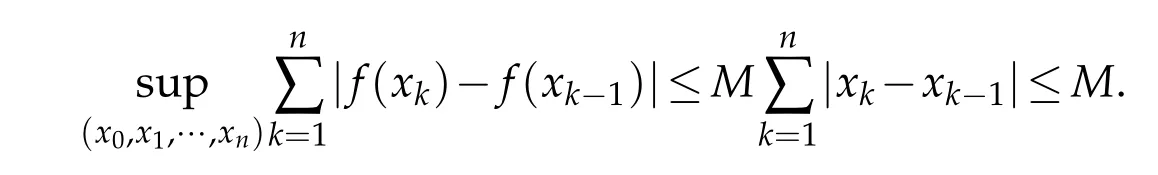
Then f（x）∈BVI.From Theorem 3.1，we can prove dimBG（f，I）=1.

Theorem 3.2.If f（x）∈C（I）∩BVI，we have

Proof.Since f（x）∈C（I）and f（x）is of bounded variation on I，by Theorem 6.6 of［6］，we know that f（x）can be replaced by the difference of two monotone increasing and continuous functions g1（x）and g2（x）.Then

where g1（x）=h1（x）-c，g2（x）=h2（x）-c，h1（1）=h2（1）=c on［1，+∞）.h1（x）and h2（x）are also monotone increasing and continuous functions.

（1）If f（0）≥0，we can choose g1（0）≥0 and g2（0）=0.By Definition 1.3，if

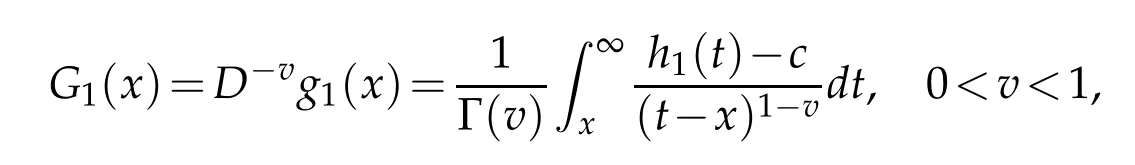
we know that G1（x）still is continuous on I when g1（x）is continuous on I.Let 0≤x1≤x2≤1 and 0＜v＜1.We have

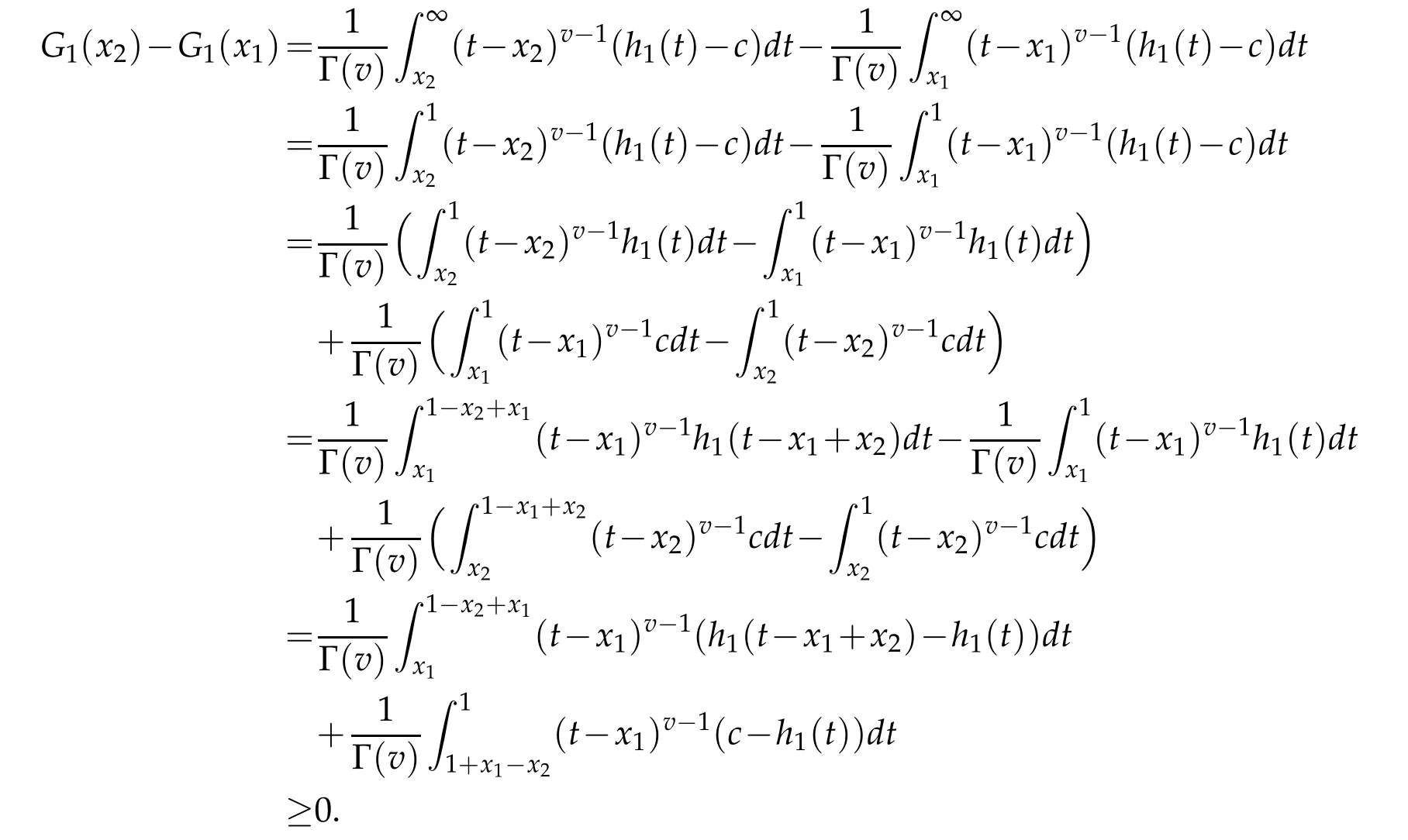
Thus function G1（x）still is a monotone increasing and continuous function on I.If

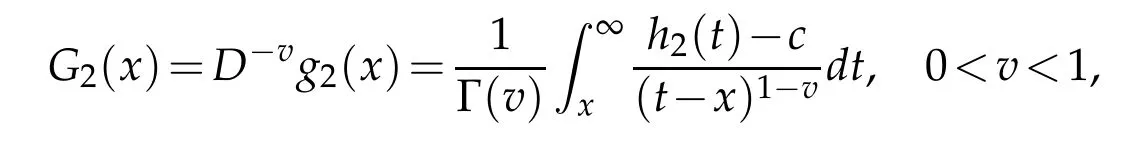
G2（x）is also a monotone increasing and continuous function on I.（2）If f（0）＜0，we can choose g1（x）=0 and g2（x）＞0.Using a similar argument，we can get that both D-vg1（x）and D-vg2（x）are monotone increasing and continuous functions on I.From Theorem 6.6 of［6］，we know D-vf（x）still is a continuous function of bounded variation on I.

4　Conclusions

The result that Box dimension of a continuous function of bounded variation on I is 1 has been proved in Theorem 3.1.Theorem 3.2 shows that Box dimension of Weyl fractional integral of such function still is 1.As we know that Box dimension of classical integral of a one-dimensional continuous function on I is 1.We consider whether Box dimension of Weyl fractional integral of a one-dimensional continuous function on I is 1 or not. From this paper，we know that Box dimension of Weyl fractional integral of a continuous function of bounded variation still is 1 on I.

However，we still can not calculate HausdorffdimensionofWeylfractional integralof continuous with bounded variation.The calculation of Hausdorff dimension is difficult. Furthermore，we only discuss fractal dimension of continuous function of bounded variation on I in this paper.We hardly know about fractal dimension of continuous function with unbounded variation.

Acknowledgements

The article is supported by NSFA 11201230.

［1］K.Falconer，Fractal Geometry:Mathematical Foundations and Application，J.Wiley Sons，New York，1990.

［2］Y.S.Liang，Box dimension of Riemann-Liouvile fractional integrals of continuous functions of bounded variation，Nonlinear Anal.，72（2010），4304-4306.

［3］B.B.Mandelbrot，The Fractal Geometry of Nature，W.H.Freeman and Company，New York，1983.

［4］K.B.Oldham，and J.Spanier，The Fractional Calculus，Academic Press，New York，1974.

［5］Z.Y.Wen，Mathematical Foundations of Fractal Geometry，Shanghai Sci.Tech.Edu.Publ. House，Shanghai，2000，in Chinese.

［6］W.X.Zheng and S.W.Wang，Real Function and Functional Analysis，High Education Publication，Beijing，1980.

［7］S.P.Zhou，K.Yao and W.Y.Su，Fractional integrals of the weierstrass functions:the exact Box dimension，Anal.Theory Appl.，20（2004），332-341.

.Email addresses:mulei fractal@sina.com（L.Mu），yaokui2015@sina.com（K.Yao），Liangyongshun@tom.com（Y.S.Liang），junwang920811@163.com（J.Wang）

4 May 2015；Accepted（in revised version）27 April 2016