A Characterization of MRA Based Wavelet Frames Generated by the Walsh Polynomials
Firdous A.Shahand Sunita Goyal
1Department of Mathematics,University of Kashmir,South Campus,Anantnag-192101,Jammu and Kashmir,India
2Department of Mathematics,JJT University,Jhunjhunu-333001,Rajasthan,India
A Characterization of MRA Based Wavelet Frames Generated by the Walsh Polynomials
Firdous A.Shah1,∗and Sunita Goyal2
1Department of Mathematics,University of Kashmir,South Campus,Anantnag-192101,Jammu and Kashmir,India
2Department of Mathematics,JJT University,Jhunjhunu-333001,Rajasthan,India
.Extension Principlesplayasignificant rolein theconstruction ofMRAbased wavelet frames and have attracted much attention for their potential applications in various scientific fields.A novel and simple procedure for the construction of tight wavelet frames generated by the Walsh polynomials using Extension Principles was recently considered by Shah in[Tight wavelet frames generated by the Walsh polynomials,Int.J.Wavelets,Multiresolut.Inf.Process.,11(6)(2013),1350042].In this paper,we establish a complete characterization of tight wavelet frames generated by the Walsh polynomials in terms of the polyphase matrices formed by the polyphase components of the Walsh polynomials.
Frame,wavelet frame,polyphase matrix,extension principles,Walsh polynomial,Walsh-Fourier transform.
AMS Subject Classifications:42C15,42C40,42A38,41A17,22B99
1 Introduction
The most common method to construct tight wavelet frames relies on the so-called Unitary Extension Principles(UEP)introduced by Ron and Shen[11]and were subsequently extended by Daubechies et al.[2]in the form of the Oblique Extension Principle(OEP). They give sufficient conditions for constructing tight and dual wavelet frames for any given refinable function φ(x),which generates a multiresolution analysis.The resulting wavelet frames are based on multiresolution analysis,and the generators are often called framelets.These methods of construction of wavelet frames are generalized from onedimension to higher-dimension,tight frames to dual frames,from single scaling function to a scaling function vector.Moreover,these principles are important because they can beused to construct wavelets from refinable functions which may not be scaling functions with desirable properties such as symmetry and antisymmetry,smoothness or compact support.To mention only a few references on tight wavelet frames,the reader is referred to[4,6,9].
The past decade has also witnesseda tremendousinterest in theproblem of constructing compactly supported orthonormal scaling functions and wavelets with an arbitrary dilation factor p≥2,p∈N(see Debnath and Shah[3]).The motivation comes partly from signal processing and numerical applications,where such wavelets are useful in image compression and feature extraction because of their small support and multifractal structure.Lang[10]constructed several examples of compactly supported wavelets for the Cantor dyadic group by following the procedure of Daubechies[1]via scaling filters and these wavelets turn out to be certain lacunary Walsh series on the real line. Kozyrev[8]found a compactly supported p-adic wavelet basis for L2(Qp)which is an analog of the Haar basis.The concept of multiresolution analysis on a positive half-line R+was recently introduced by Farkov[5].He pointed out a method for constructing compactly supported orthogonal p-wavelets related to the Walsh functions,and proved necessary and sufficient conditions for scaling filters with pnmany terms(p,n≥2)to generate a p-MRA in L2(R+).Subsequently,dyadic wavelet frames on the positive half-line R+were constructed by Shah and Debnath in[17]using the machinery of Walsh-Fourier transforms.They have established a necessary and sufficient conditions for the system{ψj,k(x)=2j/2ψ(2jx⊖k):j∈Z,k∈Z+}to be a frame for L2(R+).Wavelet packets and wavelet frame packets related to the Walsh polynomials were deeply investigated in a series of papers by the author in[13,14,18].Recent results in this direction can also be found in[6,16]and the references therein.


The rest of this paper is organized as follows.In Section 2,we introduce some notations and preliminaries related to the operations on positive half-line R+including the definitions of Walsh-Fourier transform and MRA based wavelet frames related to the Walsh polynomials.In Section 3,we prove the main result of this article,shows that a unitary polyphase matrix leads to a tight wavelet frame generated by the Walsh polynomials.
2 Walsh-Fourier analysis and MRA based wavelet frames
We start this section with certain results on Walsh-Fourier analysis.We present a brief review of generalized Walsh functions,Walsh-Fourier transforms and its various properties.
As usual,let R+=[0,+∞),Z+={0,1,2,···}and N=Z+-{0}.Denote by[x]the integer part of x.Let p be a fixed natural number greater than 1.For x∈R+and any positive integer j,we set
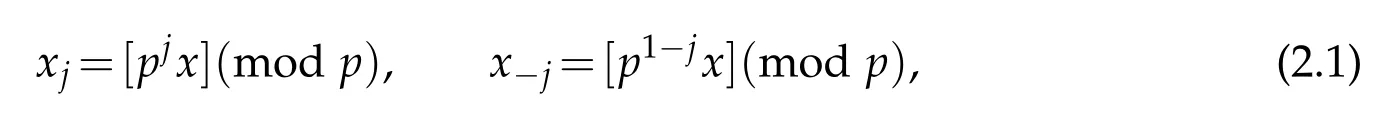
where xj,x-j∈{0,1,···,p-1}.It is clear that for each x∈R+,there exist k=k(x)in N such that x-j=0,∀j>k.
Consider on R+the addition defined as follows:

with ζj=xj+yj(mod p),j∈Z{0},where ζj∈{0,1,···,p-1}and xj,yjare calculated by(2.1).As usual,we write z=x⊖y if z⊕y=x,where⊖denotes subtraction modulo p in R+.
For x∈[0,1),let r0(x)is given by

where εp=exp(2πi/p).The extension of the function r0to R+is given by the equality r0(x+1)=r0(x),x∈R+.Then,the generalized Walsh functions{wm(x):m∈Z+}are defined by

where

They have many properties similar to those of the Haar functions and trigonometric series,and form a complete orthogonal system.Further,by a Walsh polynomial we shall mean a finite linear combination of Walsh functions.
For x,y∈R+,let

where xj,yjare given by(2.1).
We observe that

where x,y,z∈R+and x⊕y is p-adic irrational.It is well known that systems{χ(α,·)}∞α=0and{χ(·,α)}∞α=0are orthonormal bases in L2in[0,1](see Golubov et al.[7]).
The Walsh-Fourier transform of a function f∈L1(R+)∩L2(R+)is defined by


For given Ψ:={ψ1,···,ψL}⊂L2(R+),define the wavelet system


The largest A and the smallest B for which(2.5)holds are called wavelet frame bounds. A wavelet frame is a tight wavelet frame if A and B are chosen such that A=B and then generators ψ1,ψ2,···,ψLare often referred as framelets.If only the right-hand inequality in(2.5)holds,then FΨis called a Bessel sequence.
Next,we give a brief account of the MRA based wavelet frames generated by the Walsh polynomials on a positive half-line R+.Following the unitary extension principle,one often starts with a refinable function or even with a refinement mask to construct desired wavelet frames.A compactly supported function φ∈L2(R+)is called a refinable function,if it satisfies an equation of the type

where ckare complex coefficients.Applying the Walsh-Fourier transform,we can write this equation as

where

is a generalized Walsh polynomial,which is called the mask or symbol of the refinable function φ and is of course a p-adic step function.Observe that

Hence,letting ξ=0 in(2.7)and(2.8),we obtain

Since φ is compactly supported and in fact suppφ⊂[0,pn-1),thereforeˆφ∈εn-1(R+)and hence as a resultˆφ(ξ)=1 for all ξ∈[0,p1-n)asˆφ(0)=1.
For a compactly supported refinable function φ∈L2(R+),let V0be the closed shift invariant space generated by{φ(x⊖k):k∈Z+}and Vj={φ(pjx):φ∈V0},j∈Z.Then,it is proved in[5]that the closed subspaces{Vj:j∈Z}forms a p-multiresolution analysis(p-MRA)for L2(R+).Recall that a p-MRA is a family of closed subspaces{Vj}j∈Zof L2(R+)that satisfies:(i)Vj⊂Vj+1,j∈Z,(ii)∪j∈ZVjis dense in L2(R+)and(iii)∩
j∈ZVj={0}.We further assume that

Given an p-MRA generated by a compactly supported refinable function φ(x),one can construct a set of basic tight framelets Ψ={ψ1,···,ψL}⊂V1satisfying

where

are the generalized Walsh polynomials in L2[0,1]and are called the framelet symbols or wavelet masks.
With hℓ(ξ),ℓ=0,1,···,L,L≥p-1,as the Walsh polynomials(wavelet masks),we formulate the matrix M(ξ)as:

The so-called unitary extension principle(UEP)provides a sufficient condition on Ψ={ψ1,···,ψL}such that the wavelet systemFΨgiven by(2.4)forms a tight frame of L2(R+). In this connection,Shah[15]gave an explicit construction scheme for the construction of tight wavelet frames generated by the Walsh polynomials using unitary extension principles in the following way.
Theorem 2.1.Let φ(x)be a compactly supported refinable function andˆφ(0)=1.Then,the wavelet system FΨgiven by(2.4)constitutes a normalized tight wavelet frame in L2(R+)provided the matrix M(ξ)as defined in(2.12)satisfies

where

3 Polyphase matrix characterization of tight wavelet frames
Motivated and inspired by the construction of tight wavelet frames generated by the Walsh polynomials[15]using the machinery of unitary extension principles.In this section,we shallfirst derivethepolyphaserepresentationoftheWalshpolynomials(wavelet masks)and then establish a complete characterization of tight wavelet frames generated by the Walsh polynomials by means of their polyphase components.
The polyphase representation of the refinement mask h0(ξ)can be derived by using the properties of Walsh polynomials as
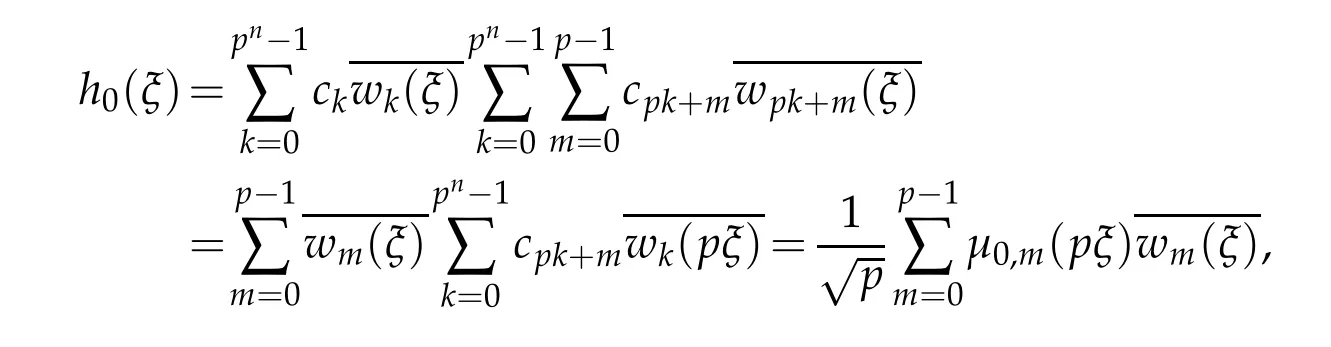
where

Similarly,the wavelet masks hℓ(ξ),1≤ℓ≤L,as defined in(2.11)can be splitted into polyphase components as

where

With the polyphase components given by(3.1)and(3.3),we formulate the polyphase matrix Γ(ξ)as:

The polyphase matrix Γ(ξ)is called a unitary matrix if

which is equivalent to

The following theorem,the main result of this paper,shows that a unitary polyphase matrix leads to a tight wavelet frame generated by Walsh polynomial on a half-line R+. Theorem 3.1.Let φ∈L2(R+)be a compactly supported refinable function and every element of the framelet symbols,h0(ξ),hℓ(ξ),ℓ=1,2,···,L,in(2.8)and(2.11)is a Walsh polynomial.Moreover,if the polyphase matrix Γ(ξ)given by(3.4)satisfy UEP condition(3.5),then the wavelet system FΨgiven by(2.4)constitutes a tight frame for L2(R+).
Proof.By Parseval's formula,we have
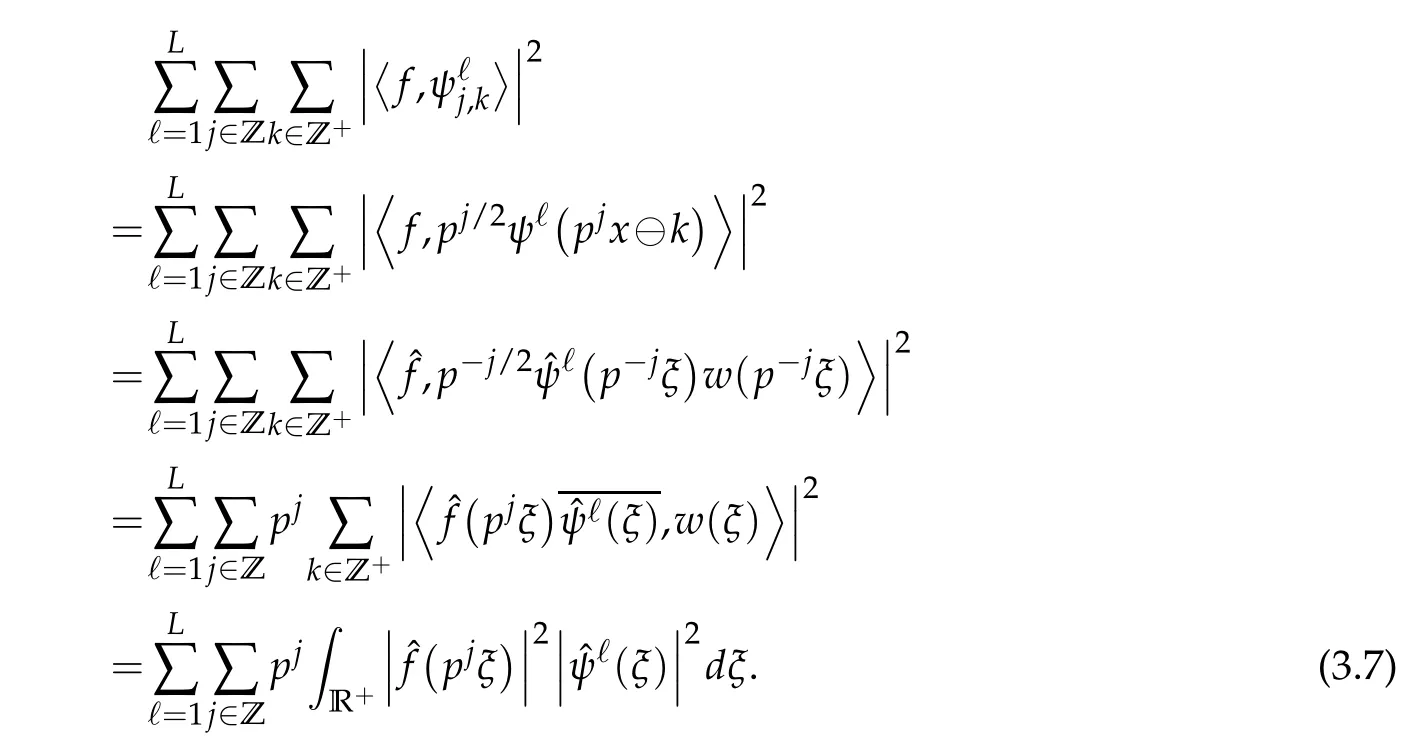
Implementing the polyphasecomponent formula(3.3)of wavelet masks hℓ(ξ),ℓ=1,···,L,we obtain

Since the polyphase matrix Γ(ξ)is unitary,which is equivalent to(3.6),the above expression reduces to

By substituting Eq.(3.8)in(3.7),we obtain

Using the assumption(2.9),the summand in the above expression can be written as

By using the above estimate in Eq.(3.9),we obtain

This completes the proof of the theorem.
Acknowledgments
The authors would like to thank the anonymous referees for their valuable successions and comments that helped to improve the overall presentation of this article.
[1]Daubechies,Ten Lectures on Wavelets,SIAM,Philadelphia,1992.
[2]I.Daubechies,B.Han,A.Ron and Z.Shen,Framelets:MRA-based constructions of wavelet frames,Appl.Comput.Harmonic Anal.,14(2003),1-46.
[3]L.Debnath and F.A.Shah,Wavelet Transforms and Their Applications,Birkh¨auser,New York,2015.
[4]B.Dong,H.Ji,J.Li,Z.Shen and Y.Xu,Wavelet frame based blind image inpainting,Appl. Comput.Harmonic.Anal.,32(2012),268-279.
[5]Yu.A.Farkov,On wavelets related to Walsh series,J.Approx.Theory,161(2009),259-279.
[6]Yu.A.Farkov,E.A.Lebedeva and M.A.Skopina,Wavelet frames on Vilenkin groups and their approximation properties,Int.J.Wavelets Multiresolut.Inf.Process.,13(6)(2015).
[7]B.I.Golubov,A.V.Efimov and V.A.Skvortsov,Walsh Series and Transforms:Theory and Applications,Kluwer,Dordrecht,1991.
[8]S.V.Kozyrev,Wavelet analysis as a p-adicspectral analysis,Izv.Akad.Nauk,Ser.Mat.,66(2)(2002),149-158.
[9]J.Krommweh,Tight frame characterization of multiwavelet vector functions in terms of the polyphase matrix,Int.J.Wavelets Multiresol.Informat.Process.,7(2009),9-21.
[10]W.C.Lang,Orthogonal wavelets on the Cantor dyadic group,SIAM J.Math.Anal.,27(1996),305-312.
[11]A.Ron and Z.Shen,Affine systems in L2(Rd):the analysis of the analysis operator,J.Funct. Anal.,148(1997),408-447.
[12]F.Schipp,W.R.Wade and P.Simon,Walsh Series:An Introduction to Dyadic Harmonic Analysis,Adam Hilger,Bristol and New York,1990.
[13]F.A.Shah,Construction of wavelet packets on p-adic field,Int.J.Wavelets Multiresolut.Inf. Process.,7(5)(2009),553-565.
[14]F.A.Shah,Non-orthogonal p-wavelet packets on a half-line,Anal.Theory Appl.,28(4)(2012),385-396.
[15]F.A.Shah,Tight wavelet frames generated by the Walsh polynomials,Int.J.Wavelets,Multiresolut.Inf.Process.,11(6)(2013),1350042.
[16]F.A.Shah,p-Frame multiresolution analysis related to the Walsh functions,Int.J.Anal. Appl.,7(2015),1-15.
[17]F.A.Shah and L.Debnath,Dyadic wavelet frames on a half-line using the Walsh-Fourier transform,Integ.Transf.Special Funct.,22(7)(2011),477-486.
[18]F.A.Shah and L.Debnath,p-Wavelet frame packets on a half-line using the Walsh-Fourier transform,Integ.Transf.Special Funct.,22(12)(2011),907-917.
.Email addresses:fashah79@gmail.com(F.A.Shah),sunitagoel2011@gmail.com(S.Goyal),
31 August 2015;Accepted(in revised version)19 April 2016
 Analysis in Theory and Applications2016年2期
Analysis in Theory and Applications2016年2期
- Analysis in Theory and Applications的其它文章
- Some Approximation Properties of Certain q-Baskakov-Beta Operators
- On Growth of Polynomials with Restricted Zeros
- Box Dimension of Weyl Fractional Integral of Continuous Functions with Bounded Variation
- Commutators ofLittlewood-PaleyOperatorsonHerz Spaces with Variable Exponent
- Commutators of Lipschitz Functions and Singular IntegralswithNon-Smooth KernelsonEuclideanSpaces
- Characterizations of Null Holomorphic Sectional Curvature of GCR-Lightlike Submanifolds of Indefinite Nearly K¨ahler Manifolds
