自黏运动绷带剥离强度力学模型研究

李玉鹏　王　其　刘昌杰　郭超群　刘　波

1.东华大学纺织面料技术教育部重点实验室(中国) 2.无锡百和织造股份有限公司(中国)



产业用纺织品

自黏运动绷带剥离强度力学模型研究

李玉鹏1王其1刘昌杰2郭超群2刘波2

1.东华大学纺织面料技术教育部重点实验室(中国) 2.无锡百和织造股份有限公司(中国)

将自黏运动绷带背部胶层设计为条状花纹，花纹宽度为2 mm，间隔为1 mm，条状花纹与宽度方向成一定角度，夹角分别为0°、15°、30°、45°和90°，基于Maxwell模型建立了自黏运动绷带剥离强度计算式，用于计算和预测此类自黏运动绷带的剥离强度，计算的剥离强度偏差百分率小于3%。

自黏运动绷带；剥离强度；模型

自黏运动绷带是在弹力绷带基布的背部涂覆一层压敏胶，直接黏贴于人体皮肤表面，它具有良好的弹性和舒适性，对运动机能增强、运动的损伤防治和康复具有一定辅助作用[1]。目前市场上多数自黏运动绷带是使用压敏胶的铺满整个基布，导致透汽性较差，剥离强度单一，无法满足不同年龄人群和人体不同部位的特殊需要。

为此，本研究中采用不连续条状胶层，使绷带具有一定的透汽性，通过改变条状胶层与宽度方向间的夹角，设计了具有不同剥离强度的系列自黏运动绷带，基于自黏运动绷带剥离瞬间压敏胶的拉伸变形，建立此类自黏运动绷带剥离强度力学模型，用于计算和预测自黏运动绷带的剥离强度。

1　自黏运动绷带中压敏胶黏弹模型分析

自黏运动绷带的剥离强度为胶接接头受外力剥离时，在自黏运动绷带宽度方向单位长度上产生的拉力，是一种线强度。剥离过程中，由于外加负荷的作用，胶黏剂产生黏弹形变，形成不连续的胶束，其180°剥离及剥离界面示意图如图1所示。

压敏胶的黏弹形变应用Maxwell模型[2](一个理想弹簧和一个理想黏壶串联)分析，模型受力时，弹簧和黏壶的应力与总应力(σ)相同，总应变(ε)为弹簧(ε1)和黏壶(ε2)的应变之和，即

图1　自黏运动绷带180°剥离及剥离界面示意图

本构方程式为

式中：E——弹性模量；

η——黏滞系数。

在此种模型下，当应变保持不变，解微分方程，可得

式中：ε0——t=0时的应变；

τ——常数。

在维持恒定形变时，有应力松弛过程。

当应力保持不变，可得蠕变方程：

当t=0时，有瞬时弹性形变产生。

假设在施加剥离负荷的瞬间，即t→0+时，形成的单根胶束应力与应变的关系为

σ=Eε

(1)

式中：E——压敏胶弹性模量，MPa；σ——剥离时拉伸成单根胶束时的应力，N/mm2；

ε——剥离时拉伸成单根胶束时的瞬时形变，mm。

2　自黏运动绷带剥离强度模型建立

本研究中，将自黏运动绷带背部胶层设计为条状花纹，花纹宽度为2 mm，间隔为1 mm，条状花纹与宽度方向成一定角度，夹角分别为0°、15°、30°、45°和90°，如图2所示。

图2　胶层花纹示意图

整片自黏运动绷带的剥离强度实质上为剥离过程中，挠性材料(运动绷带基布)作用于胶黏剂，使单位宽度上胶黏剂发生宏观形变，形成若干根胶束时抵抗外加负荷的应力，即形成的若干胶束黏弹形变的综合表现。

假设挠性材料自身性能及被黏物(钢板)的表面粗糙度对剥离强度无影响，胶层厚度不变，剥离瞬间，单位宽度(10 mm)上实际产生剥离作用的剥离有效长度为L(mm)，形成胶束的百分率(剥离时，胶束在剥离线上投影的长度占整个剥离线长度的百分比)为ω(%)。由于前排胶束还未完全与钢板分离时，后排已有胶束形成，对剥离强度产生影响，形成牵连关系，因此引入修正系数(K)修正，整片自黏运动绷带剥离强度(P)的计算式表示为

P=KLωEε

(2)

3　自黏运动绷带剥离强度模型参数确定

3.1形成胶束的百分率(ω)

试验采用5种不同花纹胶层的自黏运动绷带，条状花纹与宽度方向的夹角(θ)分别为0°、15°、30°、45°和90°。表1所示为实际测得的不同角度条状胶层的剥离有效长度(L)及形成胶束的百分率(ω)。

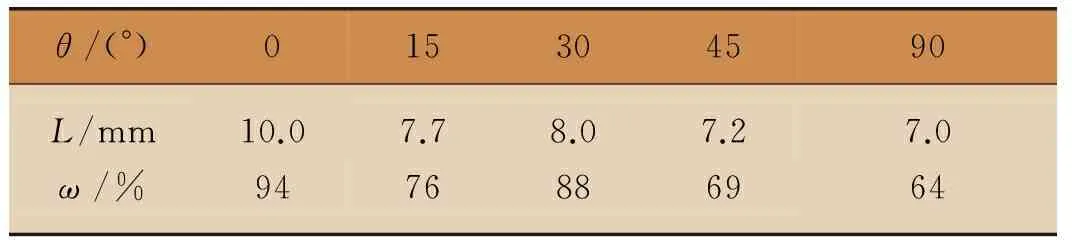
表1　不同角度条状胶层的L与ω

为了建立剥离有效长度与形成胶束的百分率之间的关系式，以剥离有效长度为自变量，形成胶束百分率为因变量，对其关系进行拟合，所得曲线如图3所示。

图3　剥离有效长度与形成胶束百分率的关系

从而得到剥离有效长度与形成胶束的百分率之间的关系式为

ω=-5.7139L2+107.38L-408.26

(3)

3.2修正系数(K)

本研究中使用的胶黏剂为深圳市安固乐科技有限公司提供的丙烯酸酯压敏胶，其弹性模量为0.3 MPa。在180°剥离过程中，假设被拉伸的胶束均为圆柱体，且其应变ε取值为3 mm，当修正系数K=1时，表示剥离过程中只有一排胶束被拉起，且其应变值相等，即只有极窄的宽度对剥离强度产生影响。将以上参数及式(3)代入式(2)中，可得K=1时，理论剥离强度(PL)(表2)。

表2　数据综合表

按照GB/T 2792—1998《压敏胶黏带180°剥离强度试验方法》[3]，试样在25 ℃条件下放置20 min，测得5组不同花纹胶层的实际剥离强度(PS)(表2)。

根据试验结果，利用自黏运动绷带的实际剥离强度(PS)与理论剥离强度(PL)的比值计算修正系数(K1)：

(4)

(5)

为验证这种人为设定的有效性，可通过计算该约定下自黏运动绷带理论剥离强度相对于实际剥离强度的偏差百分率(W1)：

(6)

计算结果见表2。可见，采用式(2)及其相关参数计算此类自黏运动绷带剥离强度偏差较大，最大偏差达37%，因此计算精度较低。

为提高计算精度，现用SPSS软件进行二次修正，得到整片自黏运动绷带剥离强度(P2)的计算式为

P2=4.489+0.485PL

(7)

二次修正后，根据式(4)～式(7)计算得到二次修正后的理论剥离强度(P2)、二次修正系数(K2)、二次修正后的剥离强度(PZ)及二次修正后的偏差百分率(W2)如表3所示。

表3　数据综合表

代入式(2)、式(3)及式(7)，则此类自黏运动绷带的剥离强度计算式为

PZ=-0.474L3+8.913L2-33.89L+5.624

(8)

由表3可见，二次修正后剥离强度偏差百分率W2小于3%，因此式(8)可用于计算和预测该类自黏运动绷带的剥离强度[4]。

4　结论

将自黏运动绷带背部胶层设计为条状花纹，花纹宽度、间隔固定不变，条状花纹与宽度方向成一定夹角，基于Maxwell模型建立了自黏运动绷带剥离强度计算式，经过二次修正，计算得到的剥离强度偏差百分率<3%，因此该计算式可用于计算和预测此类自黏运动绷带的剥离强度，指导此类系列产品的设计和选用。

[1]张洁，钱晓明.弹性绷带的发展及其在医疗领域的应用[J].棉纺织技术，2011,39(8):541-544.

[2]于伟东，储才元．纺织物理[M]．上海：东华大学出版社，2002:79-88.

[3]上海橡胶制品研究所．GB/T 2792—1998压敏胶黏带180°剥离强度试验方法[S]．北京：中国标准出版社，1998.

[4]庄楚强，何春雄.应用数理统计基础[M].广州：华南理工大学出版社，2007：32-83．

Research on physical model of peeling strength of self-adhesive sport bandage

Li Yupeng1,Wang Qi1,Liu Changjie2,Guo Chaoqun2,Liu Bo2

1.Key Lab of Textile Science and Technology,Ministry of Education,Donghua University,Shanghai/China 2.Wuxi Paiho Textile Co.,Ltd.,Wuxi/China

The self-adhesive sport bandage was designed with bar pattern adhesive layer.The bar pattern was 2 mm wide according to a separation of 1 mm.The angle were formed between bar pattern and width direction with 0,15,30,45 and 90 degrees.The formula of peeling strength of self-adhesive sport bandage was set up based on Maxwell model.It could be used to calculate and predict peeling strength of this kind of self-adhesive sport bandage.The deviation percentage calculated was less than 3%.

self-adhesive sport bandage; peeling strength; model