服装面料缝纫性能评价研究

武利利

河南科技学院 服装学院(中国)



服装与面料

服装面料缝纫性能评价研究

武利利

河南科技学院 服装学院(中国)

针对服装面料缝纫性能的影响因素，利用专家估测法对各项指标权重进行处理，应用模糊综合评判理论及系统方法，建立服装面料缝纫性能评价指标体系。将预测评判理论应用到服装面料缝纫性能的评价中，可为服装企业的生产加工提供科学依据。

面料；缝纫性能；模糊综合评判理论；专家估测

服装面料缝纫性能包括服装缝制过程中操作的难易程度，可缝性能及缝制品的外在美观状态等。缝制加工产生的服装缩皱问题在制衣生产中经常出现，它严重影响了服装产品的外观质量。目前经济发达地区的服装企业，为有效提高服装面料缝纫质量，在生产准备阶段就对服装面料缝纫性能进行相关的测试与研究，并将测试结果作为服装缝制的重要依据。对服装面料缝纫性能的预测，可有效提高服装成品质量，并为服装企业更好地适应自动化生产提供理论支持[1]。

应用模糊数学中的综合评价法评价服装面料的缝纫性能，即应用模糊分析方法处理问题，将某些定性描述和人的主观判断以量级形式表述，通过模糊运算隶属度的方式确定服装面料的缝纫性能，这对服装生产具有一定的参考价值。

1　服装面料缝纫性能指标体系建立

服装生产加工的过程就是将服装材料立体缝合成型的过程，亦即服装面料、缝线、缝制机械及操作人员动作等基本要素相互协配制作服装的过程。不同服装面料的缝纫性能各不相同。

影响服装面料缝纫性能的因素很多，主要有服装面料和缝纫线的力学性能，缝纫机针结构及其材料性能，缝纫设备及工艺参数，操作工技能等[2-3]。综合这些影响因素，建立了相应的服装面料缝纫性能评价指标体系表(表1)。

2　服装面料缝纫性能模糊综合评判

2.1方法

对一个事物的评判或评估，不能仅限于事物的某一因素，而是应涉及多个因素或多项指标，因此需要结合实际情况，根据诸多影响因素进行综合评判。模糊综合评判是对受多个因素影响的事物作出全面、综合的评价。评判是指按照给定的某些条件对事物进行评比、判别。由于各种因素所处地位不同，作用不同，在人们心目中的权重也不同，人们对于多种评判并不是绝对地采用肯定或是否定的态度，因而评判结果必然不同。服装面料模糊综合评判是通过构造服装面料缝纫性能等级的模糊子集，将反映服装面料缝纫性能的模糊指标进行量化，再通过模糊变换原理综合各项指标[4]。

表1　服装面料缝纫性能因素指标评估表

2.2步骤

2.2.1建立服装面料缝纫性能模糊综合评判因素集

设定影响服装面料缝纫性能的n个因素：

U={u1，u2，u3，…，un}

这n个因素构成服装面料缝纫性能评判因素集合。

2.2.2确定评判集合

确定服装面料缝纫性能评判等级集合为

V={v1,v2,v3，…，vm}

表示服装面料缝纫性能评判等级或分类集合，每一个等级对应相应的模糊子集，共有m个等级。

2.2.3建立服装面料缝纫性能评判等级隶属函数，构造模糊关系矩阵

根据隶属函数关系可确定各指标实际值的隶属度，由此对每个因素进行评价，得到隶属度模糊关系矩阵。

设第i(i=1,2,3，…，n)个因素的单因素评判为Ri=(ri1,ri2,ri3，…，rim)，可视作服装面料缝纫性能评判等级集合V上的一个对应映射模糊子集，其中rik(k=1,2,3，…，m)表示第i个缝纫影响因素的评判对第k个评判等级的隶属度，由此得出n个因素总的评判矩阵为

2.2.4计算服装面料缝纫性能影响因素权重模糊向量

综合考虑每个服装面料缝纫因素对评判等级所起的作用，在进行综合评判服装面料缝纫性能时，根据作用大小分别确定相应的权重，由此组成每个因素的权数分配矩阵。利用专家估测的方法，k位服装行业专家分别独立给出每个缝纫影响因素ui(i=1,2,3，…，n)的权重aij，取各因素权重平均值作为该因素权重：

(1)

即得权重分配为A=(a1,a2,a3，…，an)。

2.2.5计算服装面料缝纫性能模糊综合评价集，进行模糊综合评判

根据模糊变换原理，得到服装面料缝纫性能模糊综合评判模型，模糊综合评判的数学运算方法表示如下:

B=A·R

(2)

其中：B即为服装面料缝纫性能综合评判的结果，它直接映射了评判等集集合V上的一个模糊子集[5-10]。

3　应用举例

3.1服装面料缝纫性能指标体系各级权重的确定

利用专家估测法，请服装企业专家(包括服装公司总监、服装企业生产部长、服装企业车间主任、技术部长、组长，以及从事服装生产管理老师等)，分别给出各因素所占权重，取各因素权重的平均值作为该因素权重，具体如表2所示。

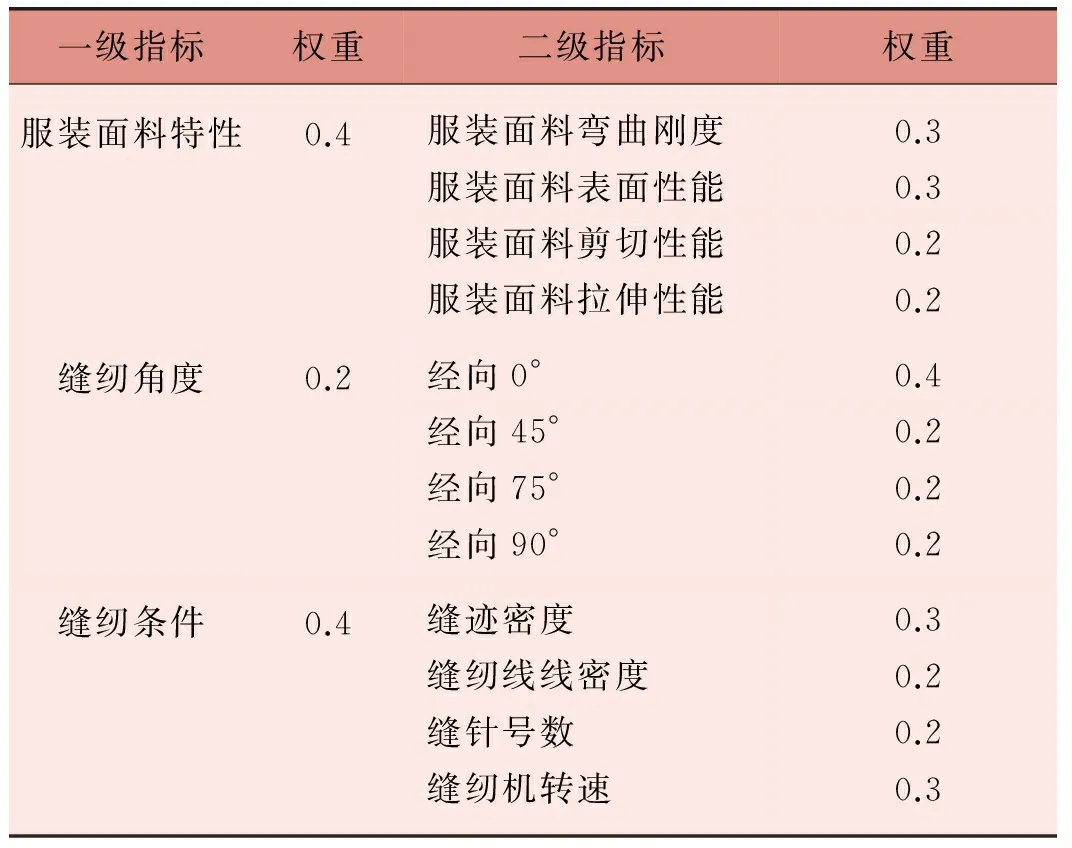
表2　缝纫评价指标及权重值

即权重分配A=(0.4,0.2,0.4),

A1=(0.3,0.3,0.2,0.2)

A2=(0.4,0.2,0.2,0.2)

A3=(0.3,0.2,0.2,0.3)

3.2确定服装面料缝纫性能评判等级及其相应标准

服装面料缝纫性能评判集为V={v1，v2，v3，…，vm}，本例中确定服装面料缝纫性能评判等级为4级，即

V={v1，v2，v3，v4}

v1——可缝纫性很好(一级)；

v2——可缝纫性较好(二级)；

v3——可缝纫性较差(三级)；

v4——可缝纫性很差(四级)。

请若干专家对一种服装面料和缝纫工艺条件进行评判打分，得到隶属函数模糊关系矩阵。例如对于缝迹密度，可缝纫性很好占45%，可缝纫性较好占30%,可缝纫性较差占15%,可缝纫性很差占10%，则得到权重分配A=(0.45,0.30,0.15,0.10)。

将二级指标各单因素评价综合成为评价矩阵R1、R2和R3：

作一级综合评判得：

B1=A1·R1=(0.32,0.27,0.24,0.12)

B2=A2·R2=(0.28,0.25,0.23,0.24)

B3=A3·R3=(0.35,0.27,0.19,0.24)

故：

对第一级因素集U={U1,U2,U3},权重分配为A=(0.4,0.2,0.4)，作二级综合评判得，B=A·R=(0.32,0.27,0.22,0.21)。按照模糊综合评判最大隶属原则，该种服装面料各项因素的综合模糊评判集B中0.32最大，即表明该服装面料的缝纫性能为一级，可缝纫性很好。

4　结语

采用试验方法测试服装面料的各项缝纫性能指标，应用模糊数学综合评判的方法，对面料的可缝纫性能进行一定程度的预测，能在服装生产中起到一定的积极指导作用。

通过提前预测服装面料的可缝纫性，可使服装企业降低成本，节省加工时间，更快地适应现代服装生产快速反应的特征，为服装企业的优化生产提供科学依据。

[1]陈霞.面料缝纫加工性能影响缝纫条件的选择[J].江苏纺织,2008(1)：56-59.

[2]武利利.薄型丝织物缝纫工艺条件与缝纫起皱关系研究[D].杭州：浙江理工大学,2012.

[3]徐蓉蓉,张欣.服装面料成衣加工性能的研究与应用[J].针织工业,2005(7)：27-31.

[4]谢季坚,刘承平.模糊数学方法及其应用[M].武汉：华中科技大学出版社,2006:190-250.

[5]孙瑛，陈广桐.模糊数学方法在湖泊水质评价中的应用[J].山东工业大学学报,1994,24(2)：155-158.

[6]阮连法,温海珍.模糊综合评价在工程投标报价中的应用[J].建筑经济，2002(2)：32-35.

[7]汪培庄.应用模糊数学[M].北京：北京经济学院出版社,1989:160-167.

[8]段永惠.模糊综合评价在土壤环境质量评价中的应用研究[J].农业系统科学与综合研究，2004,20(4)：302-305.

[9]刘锋国.基于不确定推理的继电器产品选型设计[D].天津：河北工业大学,2008.

[10]程芳.基于模糊综合评判理论的计量实验室认证[J].计量技术，2005(2)：46-48.

Study on the fabric sewing performance evaluation

Wu lili

Fashion College,Henan Institute of Science and Technology,Xinxiang/China

The fabric sewing performance evaluation system was established on influencing factors of fabric sewing performance,according to each index weight handled through expert estimation methods and on the basis of the application of fuzzy comprehensive evaluation theory and methods.The theory applied to evaluation of the fabric sewing performance would provide a scientific basis for production garment enterprises.

fabric; sewing performance; fuzzy comprehensive evaluation; expert estimation