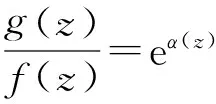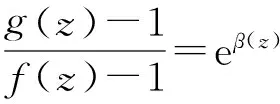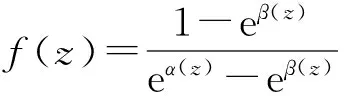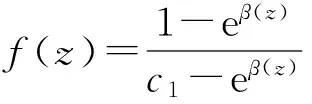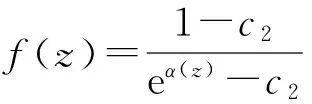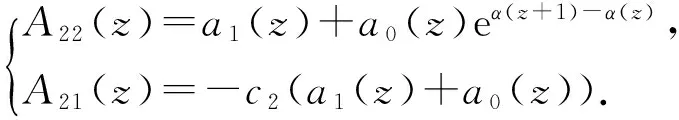一类差分方程的亚纯解与亚纯函数分担3个值的唯一性

崔　宁, 陈宗煊

(华南师范大学数学科学学院, 广州 510631)



一类差分方程的亚纯解与亚纯函数分担3个值的唯一性

崔宁, 陈宗煊*

(华南师范大学数学科学学院, 广州 510631)

利用亚纯函数的Nevanlinna值分布理论和分类讨论的思想方法, 研究了差分方程a1(z)f(z+1)+a0(z)f(z)=0的有穷级亚纯解f(z)与任一亚纯函数g(z)分担0, 1, ∞CM时的唯一性问题, 得到f(z)≡g(z)或者f(z)g(z)≡1, 其中a1(z)和a0(z)是非零多项式且满足a1(z)+a0(z)≢0.

亚纯函数; 差分方程; 分担值; 唯一性

1　引言与主要结果

本文假设读者熟悉亚纯函数值分布理论的基本内容和标准记号[1-3]. 亚纯函数通常指定义在整个复平面上的亚纯函数.

设f(z)和g(z)为亚纯函数,a为任一复数. 若f(z)-a和g(z)-a的零点相同且每个零点的重级也相同, 则称f(z)和g(z)分担aCM. 特别地, 若f(z)和g(z)的极点相同且每个极点的重级也相同, 则称f(z)和g(z)分担∞CM.

亚纯函数的唯一性理论主要探究在什么情况下只存在一个函数满足所给的条件. 例如五值定理[3]173所述: 如果2个非常数亚纯函数f和g具有共同的取5个值的点集, 则f≡g. 即任一非常数亚纯函数可由其5 个值的点集确定. 下面是经典的四值定理.

定理A[3]245设f(z)和g(z)为非常数亚纯函数,aj(j=1,2,3,4)为4个判别的复数, 且aj(j=1,2,3,4)为f(z)与g(z)的CM公共值. 如果f(z)≢g(z), 则f(z)=T(g(z)), 其中T为一个分式线性变换.

后来, 亚纯函数唯一性理论的研究得到了不断发展和完善, 取得了许多重要成果[3-7]. 随着差分及差分方程理论研究的发展[8-15], 唯一性也常与差分及差分方程的解结合起来进行研究[10-13], 这也是本文研究的主要方向.

CHEN和SHON[14]考虑了线性差分方程

Pn(z)f(z+n)+…+P1(z)f(z+1)+P0(z)f(z)=0

(1)的亚纯解的增长级，其中P0(z),…,Pn(z)均为多项式且满足P0(z)Pn(z)≢0, 并得到了如下定理:

定理B[14]设Pn(z),…,P0(z)为多项式,使得PnP0≢0且满足

Pn+…+P0≢0,

(2)

则方程(1)的每一个有穷级超越亚纯解f(z)(≢0)均满足σ(f)≥1,f(z)取每一个非零常数a无穷多次且(f-a)=σ(f).

注记1文献[14]指出在式(2)的条件下方程(1)可能有非零有理函数解. 例如, (z+1)f(z+1)-zf(z)=0 有1个有理函数解f(z)=1/z.

本文主要考虑方程(1)在n=1时的亚纯解与任意一个亚纯函数CM分担3个值的唯一性问题, 得到了如下结论.

定理1设a1(z)和a0(z)是非零多项式且满足a1(z)+a0(z)≢0. 假设f(z)(≢0)是差分方程

a1(z)f(z+1)+a0(z)f(z)=0

(3)

的一个有穷级亚纯解. 如果g(z)是任一亚纯函数且与f(z)分担0,1,∞CM,那么f(z)≡g(z)或者f(z)g(z)≡1.

例1函数f(z)=ez是差分方程f(z+1)-ef(z)=0的有穷级整函数解. 在该方程中a1(z)=1,a0(z)=-e, 则a1(z)+a0(z)=1-e≠0. 对于g(z)=e-z, 显然f(z)与g(z)分担0,1,∞CM且f(z)g(z)≡1. 这个例子说明了定理1中f(z)g(z)≡1的情形可能发生.

2　一些引理

证明由α(z)=anzn+an-1zn-1+…+a0可知

α(z+1)=an(z+1)n+an-1(z+1)n-1+…+a1(z+1)+a0=

a1+a0).从而得到

(an+an-1+…+a1).

注意到an≠0, 所以deg(α(z+1)-α(z))=n-1.

类似地, 可以得到

(bn+bn-1+…+b1).

由bn≠0 可知deg(β(z+1)-β(z))=n-1. 另外，

α(z+1)+β(z)-α(z)-β(z+1)=α(z+1)-α(z)-

(β(z+1)-β(z))=n(an-bn)zn-1+

其中Qn-3(z)是次数不超过n-3的多项式.

引理2[15]设f(z)是级为σ=σ(f)的亚纯函数且σ<+∞,η为非零常数. 那么对于每一个ε>0, 有

T(r,f(z+η))=T(r,f(z))+O(rσ-1+ε)+O(logr).

引理3[3]79-80设fj(z)(j=1,2,…,n;n≥2)为亚纯函数,gj(z)(j=1,2,…,n)为整函数, 则fj(z)≡0 (j=1,2,…,n)，若fj(z)和gj(z)满足下列条件：

(ii)当1≤j

(iii)当1≤j≤n, 1≤h

3　定理1的证明

注意到f(z)与g(z)分担0,1,∞CM. 对函数g(z)使用Nevanlinna第二基本定理, 则

3T(r,f)+S(r,f)+S(r,g).

类似可得T(r,f)≤3T(r,g)+S(r,f)+S(r,g). 所以,T(r,g)=O(T(r,f))+S(r,f)且g(z)也是有穷级亚纯函数.

由f(z)与g(z)分担0,1,∞CM可知, 存在多项式α(z)与β(z), 使得

(4)

(5)

如果eα(z)≡eβ(z),由式(4)与式(5)可知f(z)≡g(z).

下面假设eα(z)≢eβ(z). 由式(4)与式(5)可知

(6)

如果α(z)与β(z)均为常数且满足eα≠eβ, 那么由式(6)可知f(z)(≢0)为常数, 从而由方程(3)可知,a1(z)+a0(z)≡0, 矛盾. 下设α(z)与β(z)中至少有1个不是常数，分以下3种情形进行证明.

情形1.α(z)为常数且β(z)为非常数多项式. 设eα=c1(≠0)为常数.

如果c1=1, 由式(4)可知f(z)≡g(z).

如果c1≠1, 则可将式(6)改写为

(7)

将式(7)代入方程(3), 得到

A13(z)eβ(z)+β(z+1)+A12(z)eβ(z)+A11(z)eh0(z)≡0,

(8)

其中h0(z)≡0且

4.规范组织生活。可以参照在职的党员组织生活的做法，逐步规范服务社党员的组织生活。譬如：组建党支部将退休职工党员编入的一个基层支部，坚持“三会一课”制度，既采取了学理论原文、读书读报等传统的学习方式，又采取了播放电教片、开展时势论坛、主题发言、集体政治生日会等形式多样的组织活动。

因为deg(β(z+1)-β(z))=degβ(z)-1 且eβ(z)有正则增长级, 所以T(r,eβ(z+1)-β(z))=o{T(r,eβ(z))}.由引理2可知, 对于j=1,2,3,有

对式(8)使用引理3, 得到A1j(z)≡0 (j=1,2,3). 由A13(z)≡0 可知a1(z)+a0(z)≡0, 矛盾.

情形2.β(z)为常数且α(z)为非常数多项式. 设eβ=c2(≠0)为常数.

如果c2=1, 由式(5)可知f(z)≡g(z).

如果c2≠1, 则可将式(6)改写为

(9)

将式(9)代入方程(3), 可得

A22(z)eα(z)+A21(z)eh0(z)≡0,

(10)

其中h0(z)≡0且

T(r,A2 j(z))=o{T(r,eα(z)-h0(z))}(j=1,2).

情形3.α(z)与β(z)均为非常数多项式且满足eα(z)≢eβ(z).将式(6)代入方程(3), 得到

a1(z)eα(z)+a0(z)eα(z+1)-a1(z)eβ(z)-a0(z)eβ(z+1)-

a1(z)eα(z)+β(z+1)-a0(z)eα(z+1)+β(z)+

(a1(z)+a0(z))eβ(z)+β(z+1)=0.

(11)

下面根据多项式α(z)与β(z)的次数关系，分3种情况进行讨论.

情形3.1. degα(z)>degβ(z)≥1. 式(11)可改写为

A32(z)eα(z)+A31(z)eh0(z)=0,

(12)

其中h0(z)≡0且

由deg(α(z+1)-α(z))=degα(z)-1及degα(z)>degβ(z)可知deg(α(z+1)+β(z)-α(z))

T(r,eα(z+1)-α(z))=o{T(r,eα(z))},

T(r,eβ(z))=o{T(r,eα(z))},

T(r,eβ(z+1))=o{T(r,eα(z))},

T(r,eα(z+1)+β(z)-α(z))=o{T(r,eα(z))},

T(r,eβ(z+1)+β(z))=o{T(r,eα(z))},

T(r,eβ(z+1)-β(z))=o{T(r,eα(z))}.从而得到T(r,A3j(z))=o{T(r,eα(z)-h0(z))}(j=1,2). 对式(12)使用引理3, 得到A3j(z)≡0 (j=1,2). 由A31(z)≡0可知

(a1(z)+a0(z))eβ(z)+ β(z+1)-

(a1(z)+a0(z)eβ(z+1)-β(z))eβ(z)≡0.

(13)

由deg(β(z+1)-β(z))=degβ(z)-1、eβ(z)有正则增长级和引理2知,T(r,a1(z)+a0(z))=o{T(r,eβ(z+1))}及T(r,a1(z)+a0(z)eβ(z+1)- β(z))=o{T(r,eβ(z+1))}. 对式(13)使用引理3得a1(z)+a0(z)≡0, 矛盾.

情形3.2. degβ(z)>degα(z)≥1. 式(11)可改写为

A43(z)eβ(z)+β(z+1)+A42(z)eβ(z)+A41(z)eh0(z)=0,

(14)

其中h0(z)≡0且

因为degβ(z)>degα(z)及deg(β(z+1)-β(z))=degβ(z)-1,则deg(α(z)+β(z+1)-β(z))

T(r,eβ(z+1)-β(z))=o{T(r,eβ(z))},

T(r,eα(z)+β(z+1)-β(z))=o{T(r,eβ(z))},

T(r,eα(z))=o{T(r,eβ(z))},

T(r,eα(z+1))=o{T(r,eβ(z))}.

因此, 再由引理2可知, 对于j=1,2,3,有

对式(14)使用引理3, 得到A4j(z)≡0 (j=1,2,3). 由A43(z)≡0 可知a1(z)+a0(z)≡0, 矛盾.

情形3.3.degα(z)=degβ(z)=n≥1. 不妨设α(z)=anzn+an-1zn-1+…+a0,β(z)=bnzn+bn-1zn-1+…+b0,其中an(≠0),an-1,…,a0,bn(≠0),bn-1,…,b0均为常数.

如果an≠bn且an≠2bn, 则可将式(11)改写为

A54(z)eα(z)+A53(z)eβ(z)+A52(z)eα(z)+β(z+1)+

A51(z)eβ(z)+β(z+1)=0,

(15)

其中

由an≠bn及an≠2bn可知

deg(α(z)-β(z))=deg(-β(z+1))=

deg(α(z)-β(z)-β(z+1))=

deg(β(z)-α(z)-β(z+1))=n.

由引理1可得

deg(α(z+1)-α(z))=deg(β(z+1)-β(z))=

deg(α(z+1)+β(z)-α(z)-β(z+1))=n-1.

则对于j=1,2,3,4,有

对式(15)使用引理3, 得到A5j(z)≡0 (j=1,2,3,4). 由A51(z)≡0可知a1(z)+a0(z)≡0, 矛盾.

如果an=bn且eα(z)≢eβ(z), 则必有deg(α(z+i)-β(z+j))≤n-1 (i,j=0,1). 将式(11)改写为如下形式

A62(z)eα(z)+A61(z)eα(z)+ β(z+1)=0,

(16)

其中

A62(z)=a1(z)+a0(z)eα(z+1)-α(z)-a1(z)eβ(z)-α(z)-

a0(z)eβ(z+1)-α(z),

(17)

A61(z)=-a1(z)-a0(z)eα(z+1)+ β(z)-α(z)- β(z+1)+

(a1(z)+a0(z))eβ(z)-α(z).

(18)

由引理1知deg(α(z+1)-α(z))=n-1且deg(α(z+1)+β(z)-α(z)-β(z+1))≤n-2. 因为deg(-β(z+1))=n, 所以

T(r,A6j(z))=o{T(r,eα(z)-α(z)-β(z+1))}(j=1,2).

根据引理3, 得到A6j(z)≡0 (j=1,2). 结合式(17)和式(18), 得到

a0(z)(eα(z+1)-α(z)-eβ(z+1)-α(z)-eα(z+1)+β(z)-α(z)-β(z+1)+

eβ(z)-α(z))≡0.

(19)

由于a0(z)≢0, 所以式(19)可简化为

(1-eβ(z)- β(z+1))(eα(z+1)-α(z)-eβ(z+1)-α(z))≡0.

(20)

注意到eα(z)≢eβ(z). 所以由式(20)可知,eβ(z)- β(z+1)≡1. 从而得到 degβ(z)=1. 不妨假设β(z)=b1z+b0, 其中b1(≠0),b0为常数使得eb1=1. 则可设α(z)=b1z+a0, 其中a0为常数且满足eb0-a0≠1. 因此, eα(z+1)=eb1z+b1+a0≡eα(z). 将eα(z+1)≡eα(z)与 eβ(z+1)≡eβ(z)代入式(11),可得

(a1(z)+a0(z))(eα(z)-eβ(z))(1-eβ(z))≡0.

(21)

因为eβ(z)≢1且eα(z)≢eβ(z), 所以由式(21)可以得到a1(z)+a0(z)≡0, 矛盾.

(f(z)-g(z))(f(z)g(z)-1)≡0.

(22)

由式(22)可得f(z)≡g(z)或f(z)g(z)≡1.

如果an=2bn且eα(z)≢e2 β(z), 那么可将式(11)改写为

A73(z)eα(z)+A72(z)eβ(z)+A71(z)eα(z)+β(z+1)=0,

(23)

其中

deg(α(z)-β(z))=deg(-β(z+1))=

deg(β(z)-α(z)-β(z+1))=n，

以及deg(β(z)+β(z+1)-α(z))≤n-1. 根据引理1, 得到deg(α(z+1)-α(z))=deg(β(z+1)-β(z))=

deg(α(z+1)+β(z)-α(z)-β(z+1))=n-1.

所以,对于j=1,2,3, 有

对式(23)使用引理3, 可得A7j(z)≡0 (j=1,2,3). 由A73(z)≡0与A72(z)≡0可得a1(z)+a0(z)eα(z+1)-α(z)+(a1(z)+a0(z))eβ(z)+ β(z+1)-α(z)≡0,

(24)

a1(z)+a0(z)eβ(z+1)-β(z)≡0.

(25)

如果degβ(z)=n≥2, 那么deg(β(z+1)-β(z))=n-1≥1及T(r,ai(z))=o{T(r,eβ(z+1)-β(z))}(i=0,1).对式(25)使用引理3, 得到a1(z)≡a0(z)≡0, 这是一个矛盾. 所以必有degβ(z)=1. 现假设β(z)=b1z+b0,其中b1(≠0)及b0为常数. 从而可设α(z)=2b1z+a0, 其中a0是一个常数. 由eα(z)≢e2 β(z)可知ea0-2b0≠1. 由式(25)可得

a1(z)+eb1a0(z)≡0.

(26)

将a1(z)=-eb1a0(z)代入式(24), 可得

a0(z)eb1(eb1-1)(1-e2b0-a0)≡0.

(27)

由于a0(z)≢0, eb1≠0且e2b0-a0≠1, 所以由式(27)可知eb1=1. 再结合式(26)可得a1(z)+a0(z)≡0, 矛盾.

定理1证毕.

[1]杨乐. 值分布论及其新研究[M]. 北京: 科学出版社, 1982.

[2]HAYMAN W K. Meromorphic functions[M]. Oxford: Clarendon Press, 1964.

[3]仪洪勋, 杨重骏. 亚纯函数唯一性理论[M]. 北京: 科学出版社, 1995.

[4]YANG L Z. Meromorphic functions that share two values[J]. Journal of Mathematical Analysis and Applications, 1997, 209:542-550.

[5]YI H X. Meromorphic functions with two deficient values[J]. Acta Mathematica Sinica, 1987, 30(5):588-597.

[6]LI P, YANG C C. Uniqueness theorems on entire functions and their derivatives[J]. Journal of Mathematical Analysis and Applications, 2001, 253:50-57.

[7]FANG M L. Unicity theorems for algebroid functions[J]. Acta Mathematica Sinica, 1993, 36:217-222.

[8]陈宗煊, 黄志波. 复域差分和差分方程的研究[J]. 华南师范大学学报(自然科学版), 2013, 45(6):26-33.

CHEN Z X, HUANG Z B. Study on complex difference and difference equations[J]. Journal of South China Normal University (Natural Science Edition), 2013, 45(6):26-33.

[9]彭长文, 陈宗煊. 一类高阶差分方程亚纯解的性质[J]. 华南师范大学学报(自然科学版), 2014, 46(3):25-29.

PENG C W, CHEN Z X. Properties of meromorphic solutions of certain high order difference equations[J]. Journal of South China Normal University(Natural Science Edition), 2014, 46(3):25-29.

[10]CHEN Z X, YI H X. On sharing values of meromorphic functions and their differences[J]. Results in Mathematics, 2013, 63:557-565.

[11]CHEN B Q, CHEN Z X, LI S. Uniqueness of difference operators of meromorphic functions[J]. Journal of Inequalities and Applications, 2012, 48:1-9.

[12]LIU K. Meromorphic functions sharing a set with applications to difference equations[J]. Journal of Mathematical Analysis and Applications, 2009, 359:384-393.

[13]HEITTOKANGAS J, KORHONEN R, LAINE I, et al. Uniqueness of meromorphic functions sharing values with their shifts[J]. Complex Variables and Elliptic Equations, 2011, 56(1-4):81-92.

[14]CHEN Z X, SHON K H. On growth of meromorphic solutions for linear difference equations[J]. Abstract and Applied Analysis, 2013: Art 619296, 6 pp.

[15]CHIANG Y M, FENG S J. On the nevanlinna characteristic off(z+η) and difference equations in the complex plane[J]. Ramanujian Journal, 2008, 16(1):105-129.

【中文责编：庄晓琼英文责编：肖菁】

Unicity for Meromorphic Solutions of Some Difference Equations Sharing Three Values with Any Meromorphic Functions

CUI Ning, CHEN Zongxuan*

(School of Mathematical Sciences, South China Normal University, Guangzhou 510631,China)

By utilizing Nevanlinna’s value distribution theory of meromorphic functions and categorized discussion method, the uniqueness of a finite-order meromorphic solutionf(z) of the difference equationa1(z)f(z+1)+a0(z)f(z)=0 sharing 0, 1, ∞CM with any meromorphic functiong(z) is investigated, and the result is given thatf(z)≡g(z) orf(z)g(z)≡1 under the above condition, wherea1(z) anda0(z) are nonzero polynomials satisfyinga1(z)+a0(z)≢0.

meromorphic function; difference equation; shared values; uniqueness

2015-11-11《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

国家自然科学基金项目(11171119); 广东省自然科学基金项目(2014A030313422)

陈宗煊, 教授, Email: chzx@vip.sina.com.

O174.5

A

1000-5463(2016)04-0083-05