受限高浓度电解质溶液的电动力学输运
李 堃 袁志山 纪安平,3 司 伟 蔺卡宾 杨浩杰马 建 沙菁 陈云飞
(1东南大学机械工程学院,南京211189)(2东南大学江苏省微纳生物医疗器械设计与制造重点实验室,南京211189)(3重庆三峡学院机械工程学院,重庆404100)
受限高浓度电解质溶液的电动力学输运

(1东南大学机械工程学院,南京211189)(2东南大学江苏省微纳生物医疗器械设计与制造重点实验室,南京211189)(3重庆三峡学院机械工程学院,重庆404100)
为了解释有关纳米通道内离子输运特性的一系列违反经典流体力学和电迁移理论的实验现象的内在机理,通过分子动力学模拟的方法,研究了受限高浓度NaCl溶液的离子电流和迁移率等电动力学输运特性.结果显示,跨膜电压和接入电阻是导致单层石墨烯纳米孔的离子电流随孔径呈线性增长的重要原因.受限电解质溶液与体态溶液的本质区别是除了固液界面的边界效应外,跨膜电压造成的局部超大电场将导致电迁移速率随电场强度增加出现非线性增长的Wien效应.同时,离子迁移率随溶液浓度升高而下降.产生这些变化的微观机理除了离子氛屏蔽效应外,还有离子对形成和离子碰撞等离子间微观相互作用.
受限电解质溶液;纳米孔;分子动力学模拟;迁移率
随着微纳加工技术和膜片钳技术的迅猛发展,电解质溶液的电动力学输运具有越来越强的可控性和可测量性,因而被广泛应用于生物医学、分析化学、微纳机电系统等诸多领域.特别是对受限在纳米尺度下的高浓度电解质溶液的研究,被认为是实现超级电容、海水淡化、燃料电池、基因测序乃至芯片实验室等等与人类未来息息相关的环境工程与健康工程的基础[1].
但当所研究的受限流体系统达到分子尺度时,流体与固体界面间双电层效应凸显,溶质和溶剂分子的体积及其相互作用不能再被忽略,并引发了诸多与宏观尺度不同的现象.经典流体力学(Navier-Stokes方程)和经典离子电迁移理论(Poisson-Nernst-Planck方程)均假设粒子的体积忽略不计,溶液中各粒子间及其与壁面间的相互作用采用简化的平均场理论,因而当通道尺度达到纳米级或溶液浓度较高时,经典理论将会失效.例如,实验发现纳米尺度下的石墨烯缺陷可以产生线性、整流和电压门控等3种电流特性[2];当纳米通道小于0.8 nm时会出现量子化的库伦阻塞效应[3];受限在纳米碳管中的水分子有序排列成类冰体结构,组成氢键网络,不仅导致超快速Grotthuss模式的质子迁移[4],还会出现相干共振的离子电流信号[5];Duan等[6]发现受限在高2 nm的纳米通道内的Na+和K+的迁移率会明显高于高25 nm的纳米通道,但当体态溶液浓度的增加超过10-3mol/L时,离子迁移率会显著下降.
分子动力学(MD)模拟是介于实验和理论研究之间的第3种研究手段,是探索纳米尺度下溶液电动力学输运机理的重要工具[1].本文利用GROMACS经典分子动力学软件包模拟了不同浓度NaCl溶液在大电场作用下及受限在单层石墨烯纳米孔中的电动力学输运过程,探究了影响高浓度溶液离子迁移速率变化的微观机理.
1 模型建立
本文建立了2种全原子分子动力学模型:纳米孔-溶液模型和大电场溶液模型.图1(a)为纳米孔-溶液模型示意图.透明状盒子表示水分子充满整个体系.网状结构为单层石墨烯膜,C—C键长为0.142 nm,利用GMX力场来描述碳原子间的相互作用.溶液被薄膜分隔成cis和tans两部分,只能通过膜中心处的纳米孔发生物质交换,孔径为d.模拟体系沿X,Y,Z方向的尺寸均为10 nm.图1(b)为溶液在大电场(0.5 V/nm)中电迁移的模型示意图.该模型忽略了固液界面的相互影响,着重于溶液粒子间的相互作用.模拟体系沿X,Y,Z方向的尺寸分别为6,6,8 nm,采用经典的OPLS全原子力场.上述2种模型都在三维方向施加了周期性边界条件,均采用PME方法和Cut-off方法计算库伦静电作用和范德华作用.

(a) 纳米孔-溶液模型(水分子采用表面模式渲染)
(b) 大电场溶液模型(水分子采用球棍模式渲染)图1 2种分子动力学模型示意图
在模拟之前,首先对上述初始结构进行能量最小化运算,消除粒子之间可能存在的重叠现象.然后让系统在NVT系综下运行,用V-rescale耦合器使系统温度维持在300 K.为了保证系统稳定,对石墨烯薄膜最外周的碳原子进行位置限定,使其只能在平衡位置附近做热振动.当系统达到平衡后,沿Z轴负方向施加外电场,进行非平衡态模拟.
2 模拟结果分析
2.1离子水合半径
图2分别统计Na+和Cl-周围水分子的径向密度分布函数gH2O(r). 距离离子质心第1个密度峰表示离子的第1水合层.以第1密度峰下降到最低位置处的距离作为离子的水合半径[7],得到Na+和Cl-的水合半径分别为rNa+=0.34 nm和rCl-=0.36 nm.

图2 离子水合半径
2.2纳米孔-溶液模型分析
2.2.1孔径对离子电流的影响
利用纳米孔-溶液模型,保持NaCl溶液的浓度n为1 mol/L和外加电场强度E为1 V/nm的条件不变,分别对孔径为0,1,2,3,4,5,6,7,8,9 nm的10组单层石墨烯纳米孔进行非平衡态MD模拟,统计离子电流I随孔径d的变化关系,如图3(a)中圆点所示.由经典欧姆定律可知
(1)
式中,σ表示浓度为1 mol/L的NaCl溶液的电导率,且23 ℃时σ=7.75 S/m[8];ΔV为外加电压;l为膜厚.图3(a)中的虚线为根据式(1)绘制所得,显然无法拟合MD结果.
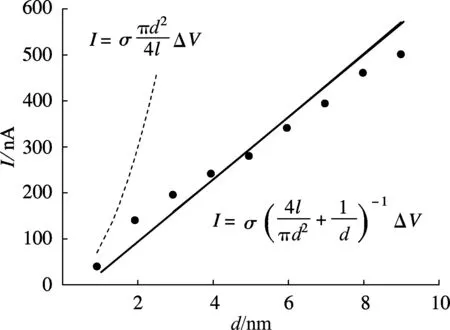
(a) 孔径对离子电流的影响

(b)电势分布函数图3 孔口电阻和跨膜电压
由于沿系统Z轴负方向施加了匀强电场,在电场力的驱动和石墨烯的阻碍作用下,离子会重新分布,出现离子极化现象.Cl-和Na+分别聚集在膜的左右两侧,形成了跨膜电势,使系统的电势降向膜的两侧附近集中.对系统沿Z方向的净电荷分布函数做2次积分,即求得Z方向的平均电势Φ,如图3(b)所示.孔径会对跨膜电压大小产生影响,而离子在石墨烯两侧沿Z方向聚集的位置不受影响,仅由离子的水合半径所决定.跨膜电势最大值和最小值的位置分别如图中2条虚线所示.随着孔径d的增加,纳米孔的电阻Rp与孔径的平方成反比,即Rp∝1/d2.当孔的长径比不大于1时,孔口的接入电阻Ra不能被忽略[9],Ra∝1/d.总电阻R=Rp+Ra,随着d的增大,Rp/Ra∝1/d减小,根据串联分压原理,分担在纳米孔上的电压(即跨膜电压)会不断下降,如图3(b)所示.尽管石墨烯膜本身的厚度仅相当于一层碳原子,约0.30nm[10],但分别加上Na+和Cl-的水合半径后,跨膜电势降的距离约为1.00nm.离子进入到孔口附近跨膜电势降范围内时,即被纳米孔捕获,因此,单层石墨烯纳米孔的有效孔长leff应当为1.0nm.当孔径为0时,跨膜电压为9.11V,小于理论上施加给系统的电压(10V),因此可以认为系统所能响应的有效电压ΔVeff=9.11V.考虑了接入电阻并修正了有效孔长和有效电压,得到离子电流计算公式如下:
(2)
根据式(2)绘制出图3(a)中的实线,很好地拟合了MD模拟的离子电流结果.
2.2.2浓度对离子电流的影响
保持单层石墨烯纳米孔的孔径d=1nm以及外加电场强度为1V/nm不变,分别对NaCl溶液浓度为0.2,0.6,1.0,1.4,1.8mol/L的5组模型进行非平衡态MD模拟,统计离子电流随溶液浓度变化规律,结果如图4中虚线所示.离子电流随着溶液浓度增加,虽然单调递增,但增长幅度逐渐减小.离子迁移率μ的计算公式如下:
(3)
式中,μ为离子迁移率;n为NaCl溶液浓度;e为元电荷量;NA为阿伏伽德罗常数.
将根据式(3)计算所得的离子迁移率μ与浓度n=1.0mol/L的NaCl溶液的离子迁移率μ0作比值,得到相对离子迁移率,如图4中实线所示.

图4 浓度对离子电流和迁移率的影响
从图4中可以明显看出相对离子迁移率随溶液浓度的增加而下降,这与之前Duan等[6]的实验结果吻合.但后者并没有给出离子迁移率变化的内在机理,只是提出如下假说:固体壁面附近形成层状的水结构,在高2 nm的纳米通道内,这种组织有序的水结构发生重叠,离子可以集中到2个水层之间, 进而改变了电迁移时的黏滞阻力.为了明确离子迁移率随NaCl浓度变化的内在机理,本文接下来将通过第2种MD模型进行详细阐述.
2.3溶液在大电场下电迁移模型分析
受限电解质溶液与体态溶液的本质区别,除了受固体壁面影响外,还有跨膜电压造成的大电场作用,例如从图3(b)的电势分布函数可以估算出单层石墨烯纳米孔内电场可以达到109V/m.带电粒子的电迁移速率在超过104V/m[11]的强电场下就不再满足Helmholtz-Smoluchowski的经典电泳理论,而是出现非线性的Wien效应[12].根据德拜理论[13], 浓度小于0.1 mol/L的NaCl溶液的德拜长度不小于1 nm,所以壁面电荷对于受限在2 nm以下的纳米通道内的稀溶液离子迁移率起主导作用[6].而当NaCl浓度达到1 mol/L以上时,静电屏蔽导致德拜长度小于0.3 nm,纳米通道内溶液的性质与体态相近,壁面的影响也随之减弱.因此,为了探究离子迁移率随浓度变化的物理本质,本文采用第2种MD模型,忽略了固液界面的相互影响,针对溶液中粒子间相互作用和大电场作用这2个主要因素.
2.3.1浓度对离子迁移率的影响
保持外加电场E=0.5 V/nm的条件不变,分别对NaCl溶液浓度为0.033,0.1,0.5,0.8,1,2,3,4 mol/L的8组模型进行非平衡态MD模拟,统计了离子迁移率,结果见图5(a).Na+和Cl-的迁移率在0.033~1 mol/L之间迅速下降,这与纳米孔-溶液模型的结果一致,证明了在该浓度条件下,固体表面对离子迁移率变化的影响已不是主要因素.当浓度从1 mol/L增加到4 mol/L时,离子迁移率仍呈下降趋势,但下降的幅度明显比浓度小于1 mol/L时小.根据修正的Debye-Hückel理论,离子迁移率随溶液浓度的升高而下降的规律被广泛认可,迁移率μ可通过下式计算[6]:
(4)
式中,参数c1,c2由环境温度T和溶剂的介电常数ε所决定,c1≈1.825(εT)-3/2,c2≈50.3(εT)-1/2(对于25 ℃的水,c1≈0.508(mol/L)-1/2,c2≈3.29(mol/L)-1/2/nm)[6];,Iz=1/2∑z2n为离子强度,z为离子价态;a为离子水合半径;μ∞为离子在无限稀释的溶液中的极限迁移率,Na+和Cl-的极限迁移率分别为5.19×10-8m2/(V·s)和7.91×10-8m2/(V·s)[5].图5(a)表示利用式(4)拟合的不同浓度下的离子迁移率,与MD模拟的结果有显著区别. 相比而言,根据式(4)计算出的离子迁移率随浓度变化趋势并不明显,主要原因在于:一方面,该理论认为迁移率与外加电场强度无关,仅由zeta电势ζ和溶液的介电常数ε及黏度η决定(μ=εζ/η),进而得到符合欧姆定律的Smoluchowski电迁移规律(v=μE),即电迁移速率v与电场强度E成正比.但是在大电场条件下,经典迁移规律将不再适用,电迁移速率v与电场强度E呈现非线性的Wien效应,即[11]
v=μ1E+μ3E3
(5)
式中,常数μ1,μ3分别通过拟合得到.另一方面,该理论没有充分考虑离子间微观相互作用,将在下文中详述.

(a) 浓度对离子电迁移速率的影响

(b) Cl-周围Na+的径向密度分布函数gNa+(r)图5 浓度效应
2.3.2电场强度对迁移率的影响
在保持NaCl浓度n=1mol/L不变的条件下,分别对溶液模型施加0.01,0.1,0.5,1.0,2.0,3.0,4.4V/nm7组不同的外电场,经过MD模拟运算,统计出离子电迁移速率随电场变化的趋势(见图6(a)),并用式(5)对模拟结果进行了拟合,标准误差小于1.4.由此可以证明在大电场条件下,欧姆定律失效,离子极限迁移率μ∞不应为固定值,μ∞和μ都应与电场强度E密切相关,这是造成Debye-Hückel理论计算与MD模拟结果有明显偏差的一个重要原因.
Debye-Hückel理论将离子氛作为浓度对离子迁移率影响的唯一因素,实际上是假设不同离子均匀分散在溶液体系中,忽略了离子的体积以及离子

(a) 外加电场对离子电迁移速率的影响

(b) Cl-周围Na+的径向密度分布函数gNa+(r)图6 大电场下的Wien效应
间的微观相互作用,如离子对作用、离子碰撞等.而分子动力学可以充分考虑系统中微观粒子间的相互作用.图5(b)和图6(b)分别统计不同模拟条件下Cl-周围Na+的径向密度分布函数gNa+(r).Na+的径向密度分布均在距离Cl-质心0.274nm处达到峰值,该距离小于Na+和Cl-的水合半径,说明2种离子可以相互进入对方的水合层内,形成离子对,直接发生相互作用.这也证明了理论假设的不合理性,离子并非均匀分散在溶液体系中,离子间的离子对作用也不能被忽略,这是导致理论失效的另一个重要原因.
从图5(b)可以看出径向密度分布的峰值随溶液浓度的升高而增长,说明与Cl-相互作用的Na+数随溶液浓度增大而单调增加,降低了离子电迁移速率.相反,图6(b)表明与Cl-相互作用的Na+数随外加电场的增强而下降,导致电场增大时电迁移速率非线性快速增长.这进一步证明了Na+和Cl-之间直接的相互作用是影响受限高浓度电解质溶液电动力学输运的重要因素,也是导致经典理论失效的关键原因.
3 结语
利用分子动力学模拟,本文修正了长径比小于1的纳米孔电流计算方法,用更简单的溶液模型说明受限高浓度电解质与体态溶液的本质区别除了固液界面的边界效应外,还有局部超大电场产生的Wien效应.通过模拟结果发现,离子迁移率随外加电场增大而出现非线性增长,且其随溶液浓度升高而下降的主要原因是离子对形成等离子间微观相互作用.这些结论合理地解释和验证了之前的实验,对以后的研究具有指导意义.
< class="emphasis_italic">References
)
[1]ThomasM,CorryB,HilderTA.Whathavewelearntaboutthemechanismsofrapidwatertransport,ionrejectionandselectivityinnanoporesfrommolecularsimulation? [J]. Small, 2014, 10(8): 1453-1465.DOI:10.1002/smll.201302968.
[2]JainT,RaseraBC,GuerreroRJ,etal.Heterogeneoussub-continuumionictransportinstatisticallyisolatedgraphenenanopores[J]. Nature Nanotechnology, 2015, 10(12): 1053-1057.DOI:10.1038/nnano.2015.222.
[3]KaufmanIK,McClintockPVE,EisenbergRS.Coulombblockademodelofpermeationandselectivityinbiologicalionchannels[J]. New Journal of Physics, 2015, 17(8): 083021.DOI:10.1088/1367-2630/17/8/083021.
[4]AgmonN.TheGrotthussmechanism[J]. Chemical Physics Letters, 1995, 244(5): 456-462.DOI:10.1016/0009-2614(95)00905-j.
[5]LeeCY,ChoiW,HanJH,etal.Coherenceresonanceinasingle-walledcarbonnanotubeionchannel[J]. Science, 2010, 329(5997): 1320-1324.DOI:10.1126/science.1193383.
[6]DuanC,MajumdarA.Anomalousiontransportin2-nmhydrophilicnanochannels[J]. Nature Nanotechnology, 2010, 5(12): 848-852.DOI:10.1038/nnano.2010.233.
[7]SukME,AluruNR.Iontransportinsub-5-nmgraphenenanopores[J]. Journal of Chemical Physics, 2014, 140(8): 084707.DOI:10.1063/1.4866643.
[8]HaynesWM. CRC handbook of chemistry and physics[M]. 91sted.BocaRaton,Florida,USA:CRCPress, 1989:613.
[9]HyunC,RollingsR,LiJ.Probingaccessresistanceofsolid-statenanoporeswithascanning-probemicroscopetip[J]. Small, 2011, 8(3): 385-392.DOI:10.1002/smll.201101337.
[10]NovoselovKS,GeimAK,MorozovSV,etal.Electricfieldeffectinatomicallythincarbonfilms[J]. Science, 2004, 306(5696): 666-669.DOI:10.1126/science.1102896.
[11]ShilovV,BaranyS,GrosseC,etal.Field-induceddisturbanceofthedoublelayerelectro-neutralityandnon-linearelectrophoresis[J]. Advances in Colloid and Interface Science, 2003, 104: 159-173.
[12]OnsagerL,KimSK.Wieneffectinsimplestrongelectrolytes[J]. The Journal of Physical Chemistry, 1957, 61(2): 198-215.DOI:10.1021/j150548a015.
[13]IsraelachviliJN. Intermolecular and surface forces[M]. 3rded.SaltLakeCity,Utah,USA:AcademicPress, 2011:312-313.
Electrokinetics transport of confined electrolyte solution in high concentration
Li Kun1,2Yuan Zhishan1,2Ji Anping1,2,3Si Wei1,2Lin Kabin1,2Yang Haojie1,2Ma Jian1,2Sha Jingjie1,2Chen Yunfei1,2
(1School of Mechanical Engineering, Southeast University, Nanjing 211189, China) (2Jiangsu Key Laboratory for Design and Manufacture of Micro-Nano Biomedical Instruments, Southeast University, Nanjing 211189, China) (3School of Mechanical Engineering, Chongqing Three Gorges University, Chongqing 404100, China)
To explain the mechanism of ion transport in nanochannel behind a series of phenomena which can not be explained by classical fluid mechanics and electrical transport theory, by all-atom molecular dynamics (MD) simulations, ionic current and ion mobility as well as other electrokinetics transport properties of confined sodium chloride solution are investigated. The results indicate that transmembrane voltage and access resistance have a significant contribution to the linear growth of the ionic current of monolayer graphene nanopore with pore diameter increasing. The essential difference between confined electrolyte solution and bulk solution is that despite the boundary effect on solid-liquid interface, ultra-high localized electrical field caused by transmembrane voltage leads to the Wien effect, that is, ion mobility nonlinearly increases with electrical field rising. Furthermore, the ion mobility decreases as the bulk concentration increases. In addition to the ionic atmosphere effect, the microscopic mechanism is the interaction between ions including ion pair formation and the ion-ion collisions.
confined electrolyte solution;nanopore;molecular dynamics simulation;mobility
10.3969/j.issn.1001-0505.2016.05.012
2016-02-16.作者简介:李堃(1989—),男,博士生;陈云飞(联系人),男,博士,教授,博士生导师,yunfeichen@seu.edu.cn.
国家自然科学基金资助项目(51435003, 51375092)、重庆市教委科学技术研究资助项目(KJ1401030)、东南大学优秀博士学位论文培育基金资助项目(KYLX_0100)、江苏省普通高校学术学位研究生创新计划资助项目(YBJJ1540).
TB383
A
1001-0505(2016)05-0972-05
引用本文:李堃,袁志山,纪安平,等.受限高浓度电解质溶液的电动力学输运[J].东南大学学报(自然科学版),2016,46(5):972-976. DOI:10.3969/j.issn.1001-0505.2016.05.012.

