郑州饱和粉土动剪切模量的试验研究

黄志全， 郭芳洁， 贾景超， 吴超， 张振华

(华北水利水电大学，河南 郑州 450045)



郑州饱和粉土动剪切模量的试验研究

黄志全， 郭芳洁， 贾景超， 吴超， 张振华

(华北水利水电大学，河南 郑州 450045)

土的动剪切模量是土动力特性非常重要的参数，动剪切模量与剪应变的关系是研究土动力特性规律的必不可少的内容之一。动剪切模量和动剪应变的关系模型可以用来描述土的动应力-动应变关系。试验选取郑州市粉土作为试验土样，并制备重塑土样，在不排水条件下使用GDS共振柱仪对饱和粉土进行动力试验，测得土样在10-6～10-3小应变范围内的动剪切模量与动剪应变。进而选用H-D模型和Davidenkov模型，对试验数据进行拟合回归分析，结果表明，Davidenkov模型能更好地描述郑州饱和粉土的动剪切模量比(G/Gmax)与动剪应变(γ)的关系。该研究可为粉土动力模型的选取和地震分析提供一定的参考依据。

饱和粉土；动剪切模量；共振柱；(G/Gmax)-γ曲线；H-D模型；Davidenkov模型

动剪切模量和阻尼比是土动力特性研究的重要参数。场地地震反应分析、土工构筑物的地震稳定性评价、土桩结构体系的动力相互作用分析和近海场地地震稳定性评估均采用等效线性方法，在使用该方法考虑土的非线性性能时，必须用到表示土的动力性能的最大剪切模量、动剪模量比-剪应变曲线、阻尼比-剪应变曲线。动剪切模量和阻尼比参数的准确测定和合理取用在很大程度上影响土工建筑物抗震设计的合理性[1-2]。

国内外很多学者对于动剪切模量与动剪应变关系进行了深入的研究。常见的模型有：Ramberg-Osgood模型，Konder模型，Hardin和Drnevich[3]提出的H-D模型，Stokoe提出的修正双曲线模型，Streete提出含动剪应力的三参数拟合模型，Martin和Seed[4]提出的三参数Davidenkov拟合模型。陈国兴等提出用塑性指数Ip描述(G/Gmax)-γ和λ-γ曲线的经验公式，并推荐了通过不同物性指标估算Gmax的经验公式[1]。彭盛恩等提出六参数的拟合方程以表示剪应变与阻尼比的直接关系[5]。袁晓铭等给出了动剪切模量比与阻尼比随剪应变变化的平均曲线、推荐线和包线[6]。

很多学者也对拟合方法、动力学参数关系及其影响因素进行了研究。黄志全等提出了岩体力学参数试验数据可靠性检验方法[7]。杨运清等研究了非线性模型拟合结果的统计检验方法的适用性[8]。李永强等分析了非线性拟合方法对拟合结果的影响[2]。王志佳对动剪切模量比与剪应变、阻尼比与剪应变进行了回归分析[9]。黄志全等研究了非饱和黄土的动剪切模量与阻尼比[10]。湛川等对弱膨胀土的固结压力、振动频率对阻尼比、剪切模量的影响进行了研究[11]。但是，对饱和粉土动剪应变与动剪切模量比的不同拟合模型的优度检验还有待研究。

本文利用GDS共振柱对郑州饱和粉土进行动力试验，测定土体的动剪切模量和剪应变，并选用H-D模型和Davidenkov模型对试验结果进行拟合。通过定性和定量分析，得出针对动剪切模量和动剪应变关系的较优的拟合模型。

1　试验方法

1.1试样制备

试验用土采用郑州市粉土。由于原状粉土易受扰动，对试验影响较大，故试验采用重塑土样。按照《土工试验方法标准》(GB/T 50123—1999)进行试样的制备。原状土经过烘干、过筛、碾压后，添加一定质量的水，搅拌均匀，并将其放置于保湿缸中，充分润湿，然后测定含水率[12]。取出该含水量的土，放入制样器中，分3层压制出圆柱形试样。试样高100 mm，直径50 mm。

1.2试验方法

试验使用GDS共振柱系统RCA，采用无弹簧支撑式、固定一端自由振动方法。该配置是通过一个驱动系统产生扭矩，在圆柱形试样的自振频率下激振试样。通过测量自由端的运动，获得传递波的速度和材料的阻尼，根据测得的速度和试样密度来计算剪切模量，其数学推导简便。该系统精确扫描的增量为0.5 Hz或0.1 Hz。试验后可以直接得到电压、频率、应变和阻尼比的试验数据。

该试验的试样含水率为10.95%，干密度为1.45 g/cm3，采用水头饱和方法，当孔压系数大于等于0.97时，认为试样已经饱和。然后对试样进行固结，当1 h内固结排水量变化不大于0.1 cm3时，认为试样固结稳定[12]。该试验在等向不排水的条件下，分别施加100、200、300 kPa围压，测定饱和粉土的动剪切模量和动剪应变。

2　拟合模型及试验结果

本文采用H-D模型和Davidenkov模型对试验结果进行拟合。

2.1模型简介

H-D模型公式如下：

(1)

式中：G/Gmax为动剪切模量比；γ、γγ分别为动剪应变、参考剪应变，无量纲。

参考剪应变与初始剪切模量G0之间存在以下关系：

G0=τmax/γγ,

(2)

式中τmax为最大动剪应力，MPa。

Davidenkov模型公式如下：

(3)

式中：A、B、γ0为与土性相关的拟合参数，无量纲；为拟合方便，以B代替2B[2]。

2.2试验结果

不同围压下，动剪切模量与动剪应变的关系、动剪切模量比与动剪应变的关系分别如图1和图2所示。

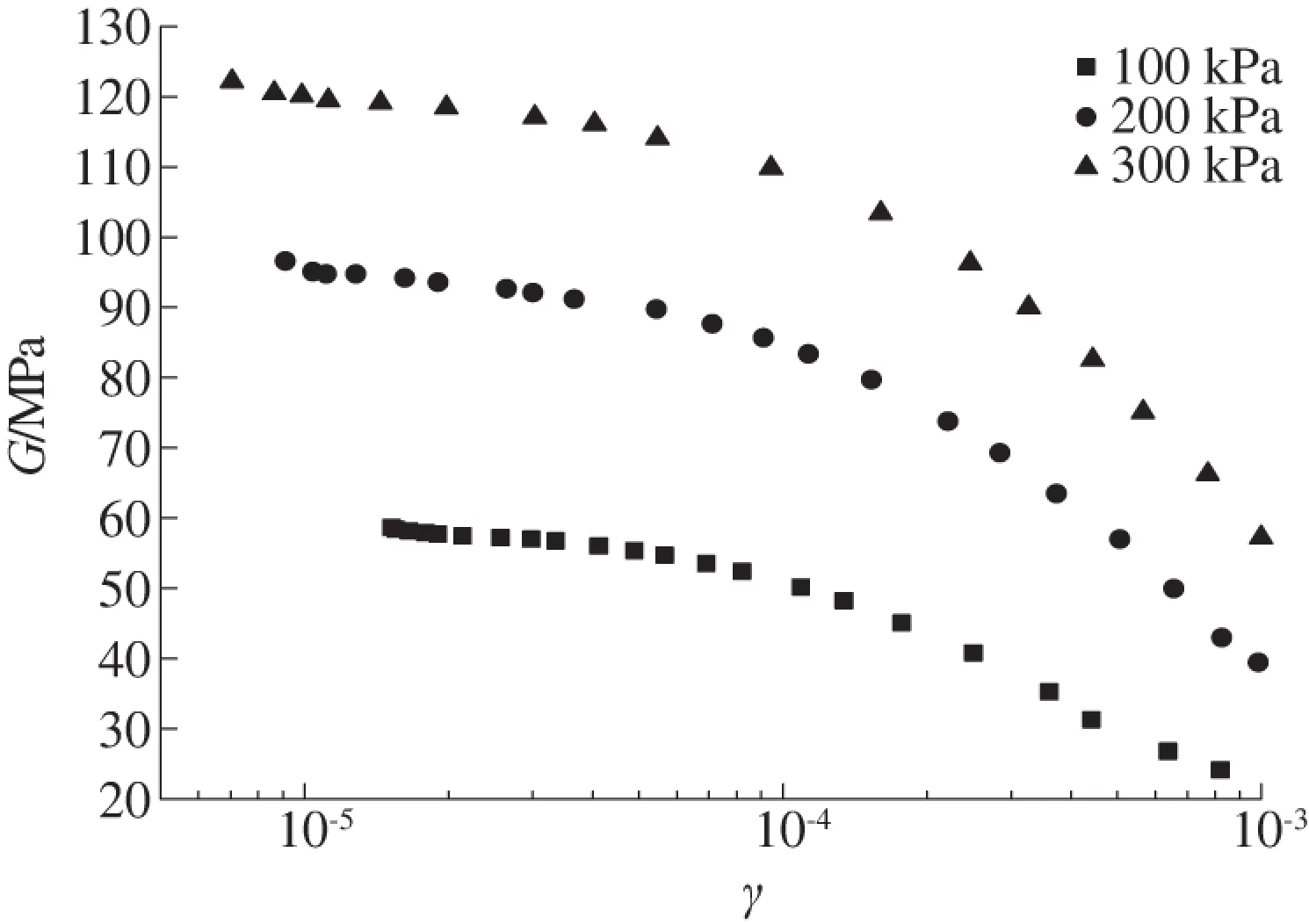
图1　不同围压下G-γ曲线

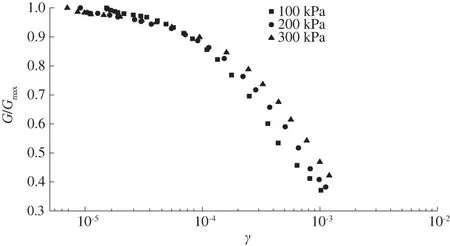
图2　不同围压下G/Gmax-γ曲线

由图1可知：不同围压的动剪切模量与动剪应变的关系符合动剪切模量随着动剪应变的增大而衰减的规律；在同一干密度、同一饱和度及同一固结比的情况下，当动剪应变一定时，动剪切模量随着围压的增大而增大；动剪切模量随动剪应变增大而衰减的速率变小。

由图2可知：不同围压下动剪切模量比随着动剪应变的增大而衰减；不同围压下的动剪模量比差值不大，在图上显示为试验数据点集中，基本都落在同一条曲线附近。这说明动剪切模量对最大动剪切模量具有较好的归一性。

3　拟合结果分析

3.1H-D模型拟合结果

H-D模型选用多个参数拟合对比，其拟合结果如图3—5所示。不同围压下H-D模型的拟合参数见表1。

从图3—5可以看出，拟合曲线随拟合参数的增大而上升，而且曲线的上升幅度总体相同。但是，在不同动剪应变范围内，拟合曲线随拟合参数变化的幅度有所差别。

关于拟合曲线随拟合参数变化的具体情况以及拟合曲线与试验数据点的具体位置关系，下面以100 kPa围压的拟合情况来分析。拟合结果如图6和图7所示。

图3　100 kPa围压下H-D模型拟合结果

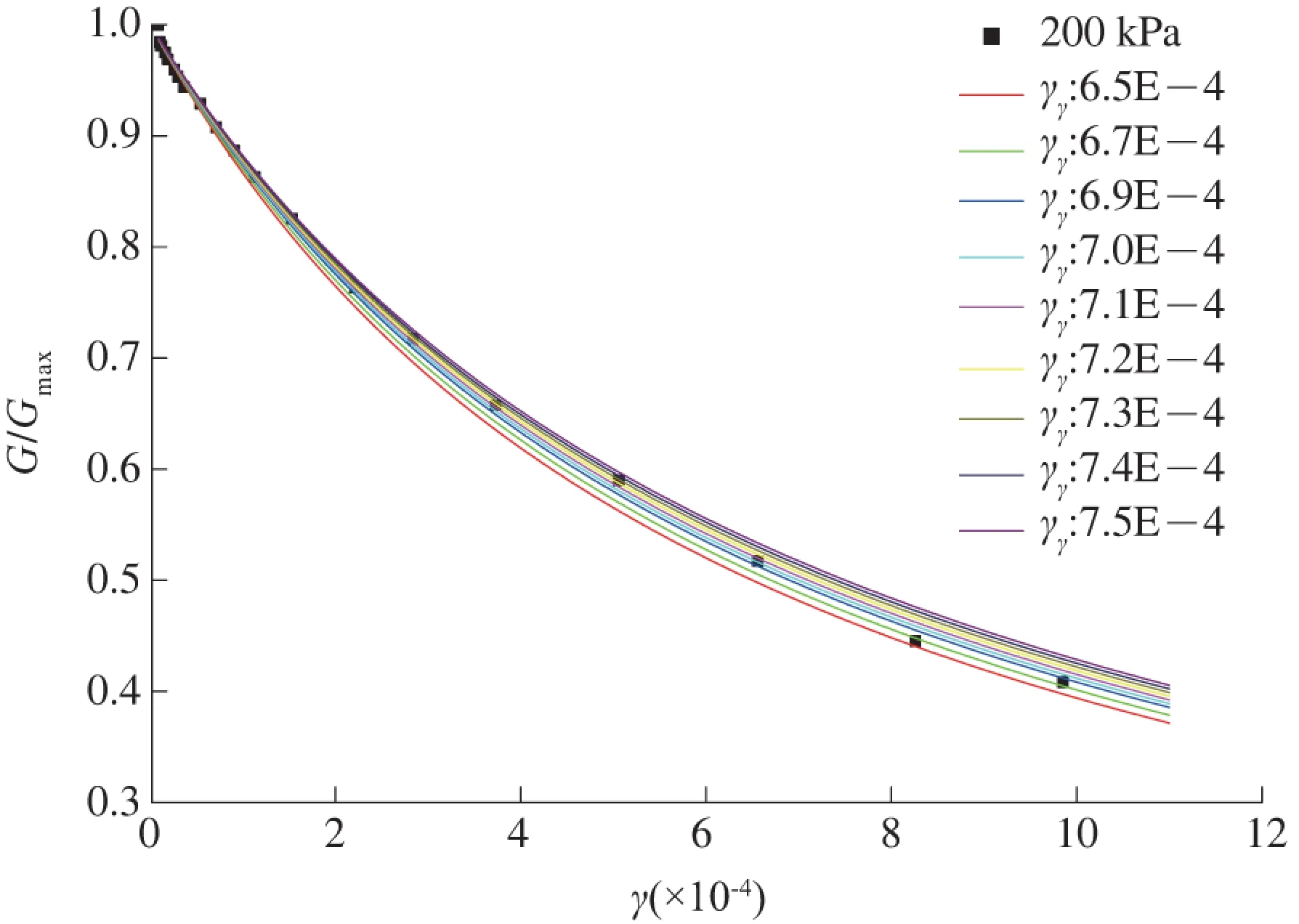
图4　200 kPa围压下H-D模型拟合结果

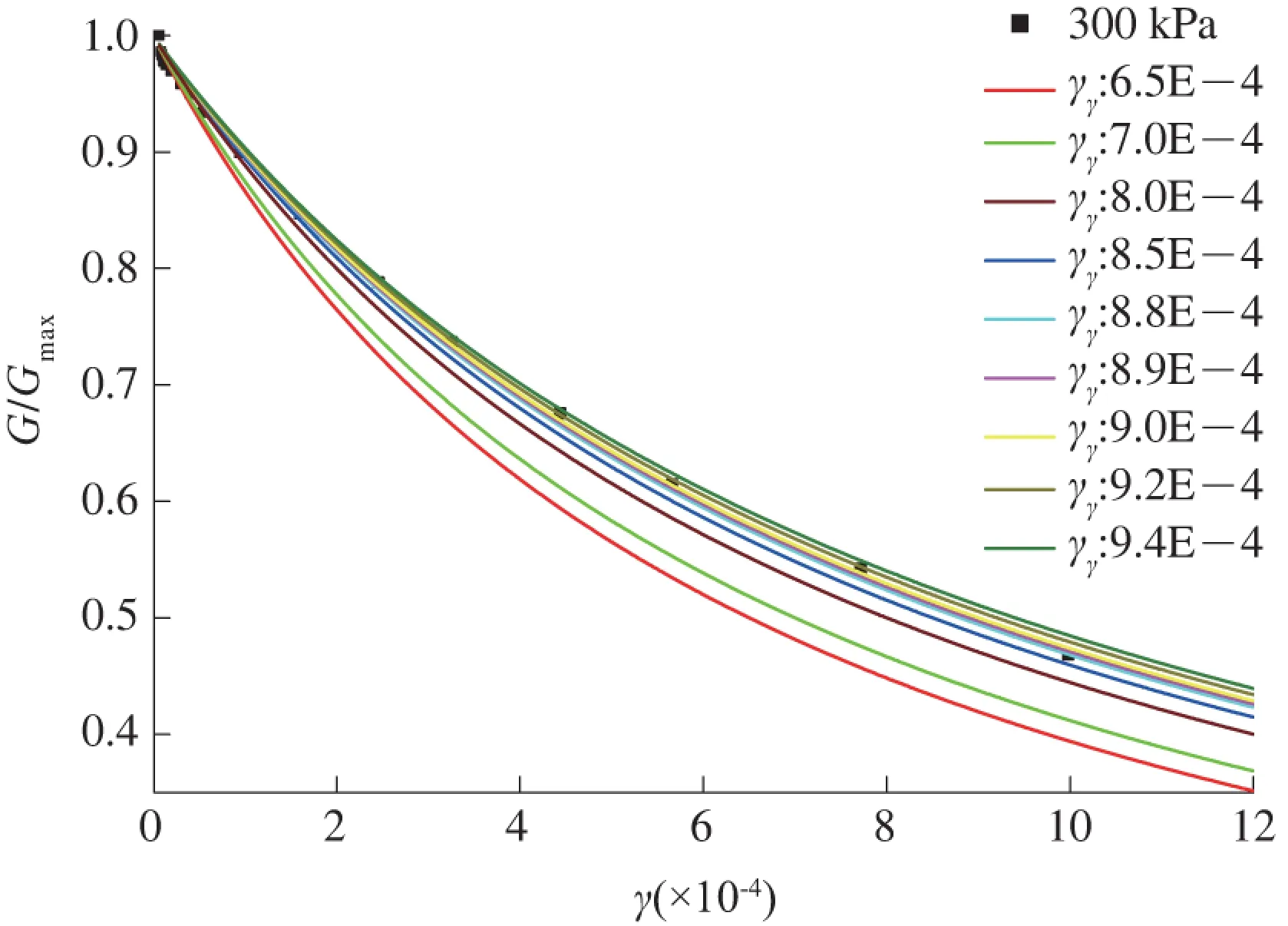
图5　300 kPa围压下H-D模型拟合结果

围压/kPa拟合参数γγ(×10-4)1005.05.25.45.55.86.06.56.92006.56.76.97.07.17.27.37.47.53006.57.08.08.58.88.99.09.29.4

由图6可知：在γ≤7E-5范围内，随着拟合参数的增大，拟合曲线上升，拟合曲线的切线具有趋于水平的变化趋势，且拟合曲线在较小应变范围内逐渐聚拢；而且，即便拟合参数为6.9E-4，拟合曲线的边界仍然只是接近试验数值点，偏离差值随着拟合参数的增大而减小。

由图7可知：在γ>7E-5范围内，试验数据点分布在很多拟合曲线之中，但是只有少部分数据点位于同一条曲线上。

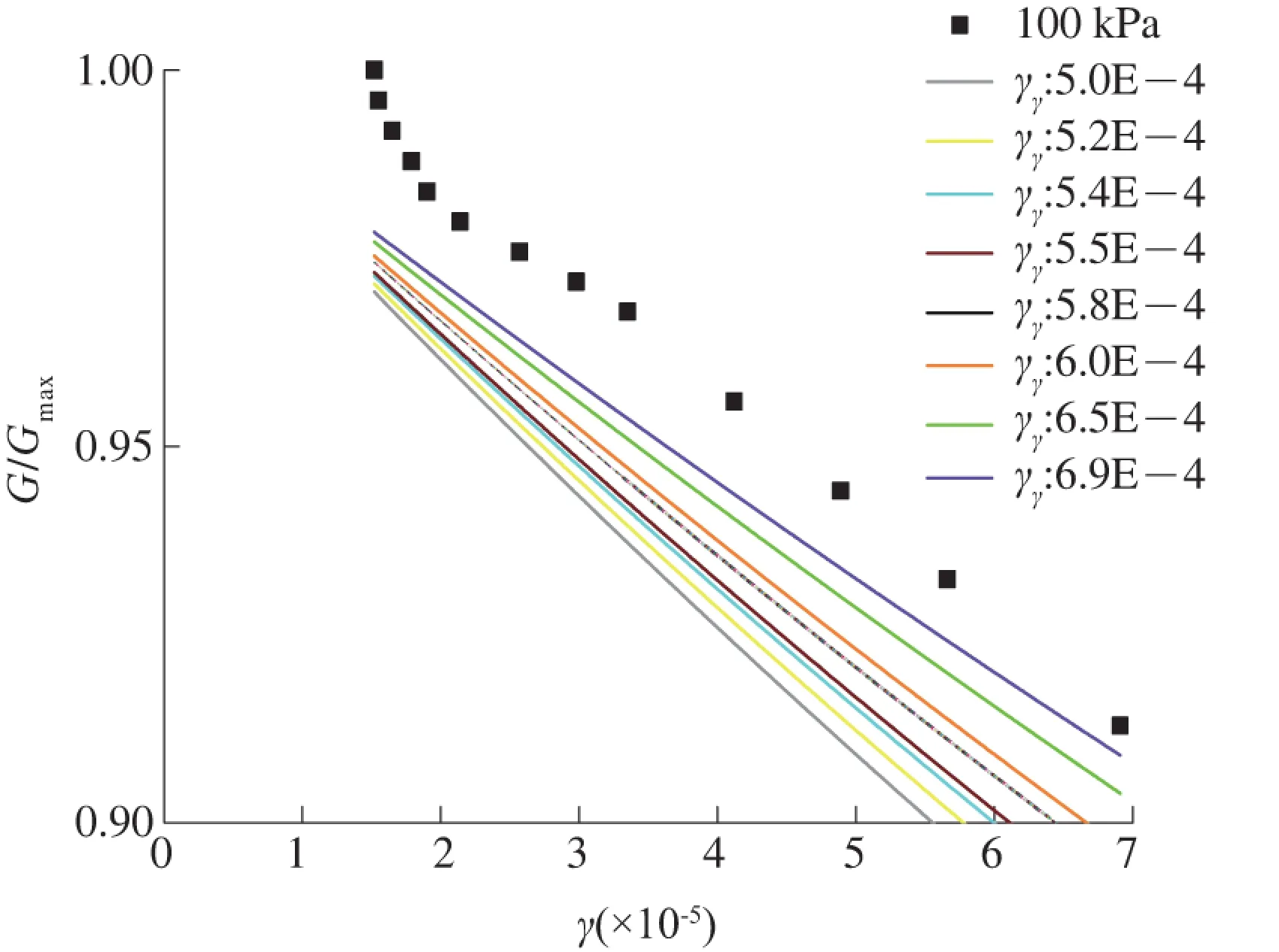
图6　100 kPa围压下H-D模型拟合结果(γ≤7E-5)

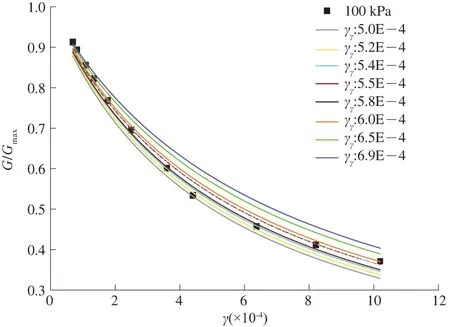
图7　100 kPa围压下H-D模型拟合结果(γ>7E-5)

围压为200 kPa时，拟合参数在6.9E-4～7.4E-4范围内，拟合情况较好，拟合参数为7.0E-4时拟合情况最佳。围压为300 kPa时，拟合参数为8.8E-4的拟合情况最佳，但仍然存在位于同条曲线上的数据点较少的现象。

3.2Davidenkov模型拟合结果

不同围压下，Davidenkov模型拟合结果如图8所示。

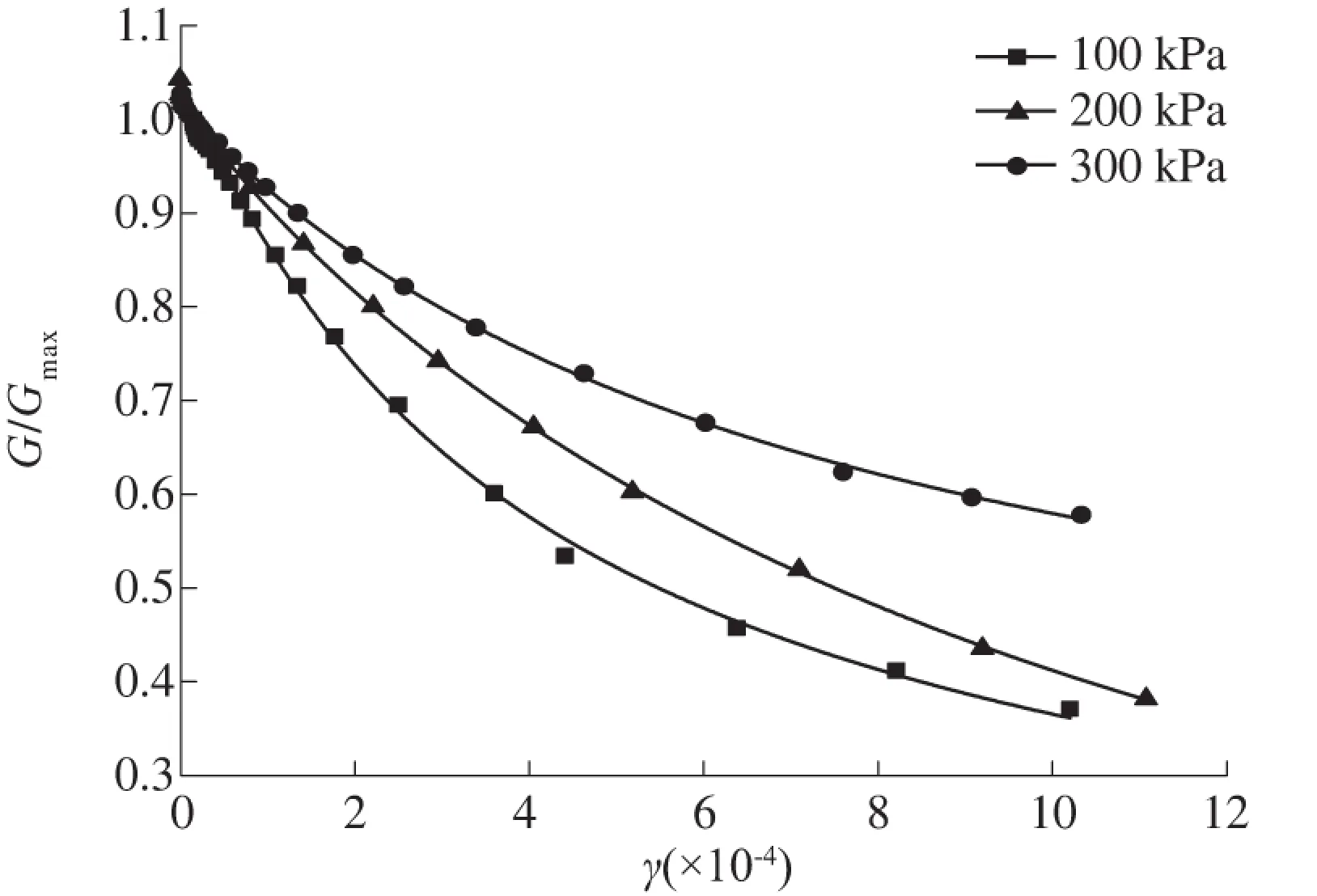
图8　不同围压下Davidenkov模型拟合结果

由图8可知，曲线几乎经过全部试验点，试验点分布在曲线的附近，拟合效果较好。

Davidenkov模型拟合参数和H-D模型最优拟合参数列于表2。

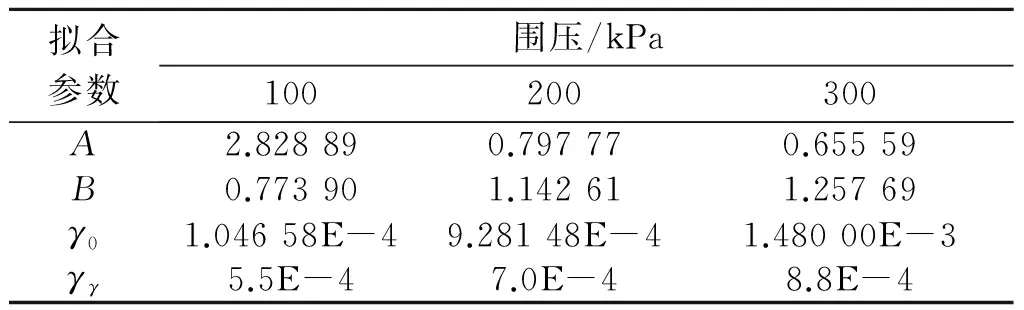
表2　最优拟合参数表

3.3拟合检验

方差分析是把变量方差分解为不同部分，比较它们之间的大小，并用F检验对回归方程进行显著性检验。F值越大，P值越小，表示结果越可靠。当P<0.01时，差异极显著；当P<0.05时，差异显著；当P>0.05时，差异不显著。F检验虽然可以间接判断所估模型参数是否为最小二乘解，但是F检验只是对实际值与估计值序列均值的差异显著性检验，故可以采用卡方检验法严格地检验模型对每个实际值的拟合情况，以判断拟合结果的可靠性[8]，即引入加权卡方检验系数RCS，其值越小，模型拟合越好。

H-D模型、Davidenkov模型的决定系数、校正决定系数、P值和RCS值见表3。

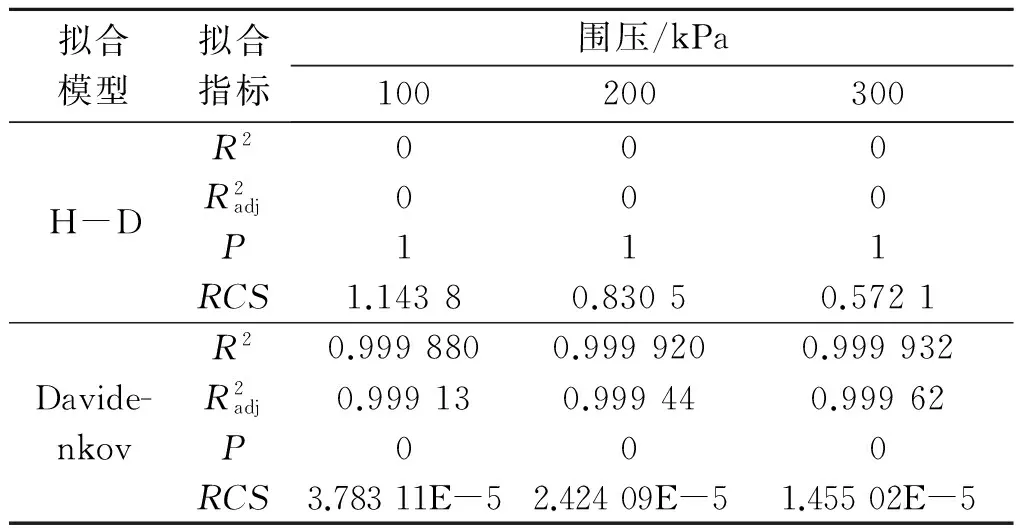
表3　拟合优度表

从表3中可知：使用H-D模型时的决定系数和校正决定系数为0，P值为1，这说明回归方程整体相关性不高，回归结果不可靠，差异不显著；Davidenkov模型的决定系数和校正决定系数均接近1，说明回归方程相关性高，P值为0，说明差异显著；Davidenkov模型的RCS值远小于H-D模型的RCS值，该模型拟合效果较好。

残差是回归方程值与试验值的差值，通过残差图可以检查回归曲线的异常点，即回归拟合的检验问题。本文以残差值为纵坐标，动剪应变为横坐标，绘制残差图。残差值越接近于0分布，说明回归曲线拟合值与试验值差值越小，回归曲线与试验点越接近，拟合程度越好；残差值分布越随机，说明动剪切模量比的残差值与动剪应变值越独立，拟合程度越好。H-D模型、Davidenkov模型的动剪切模量比的残差图分别如图9和图10所示。

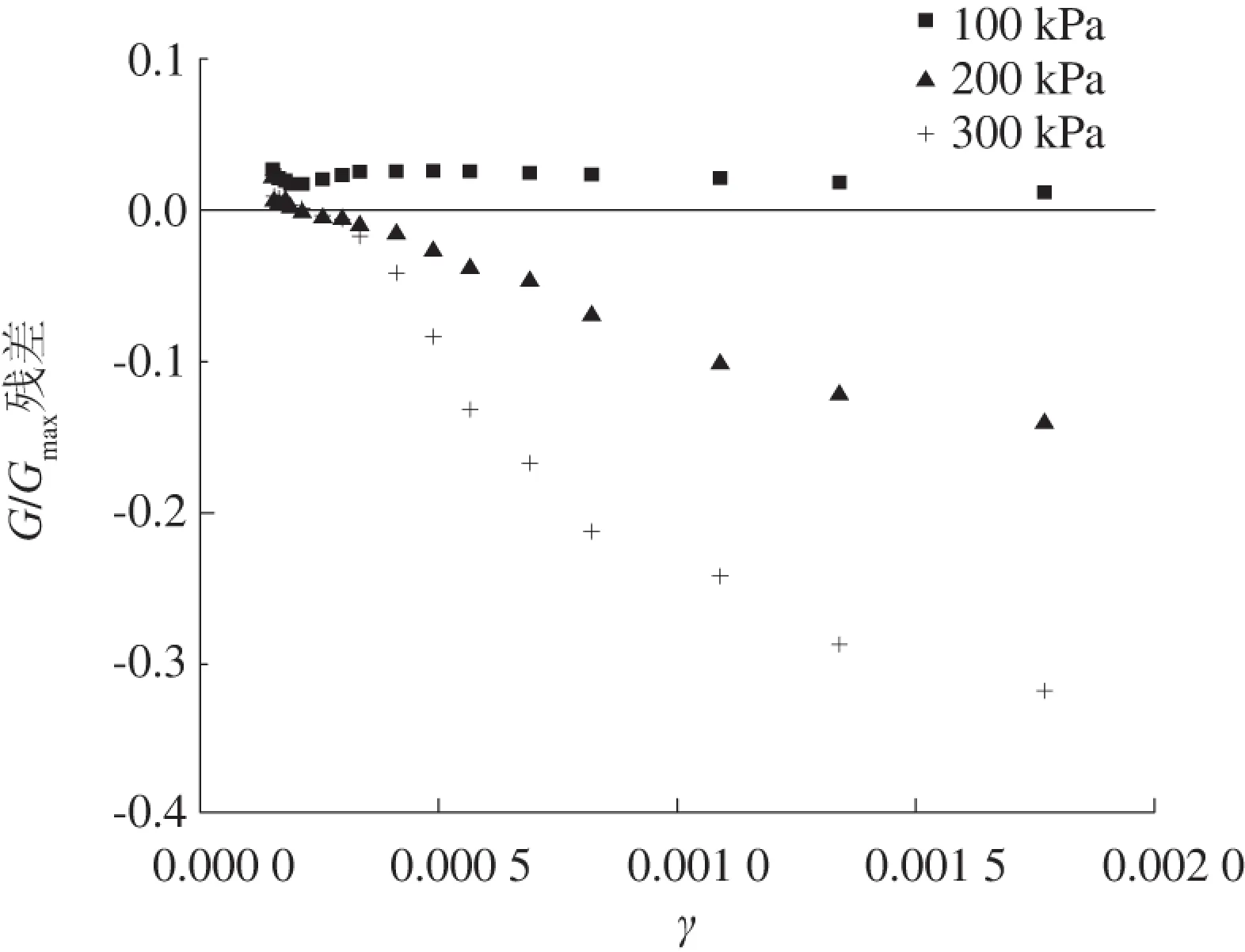
图9　H-D模型动剪切模量比残差图

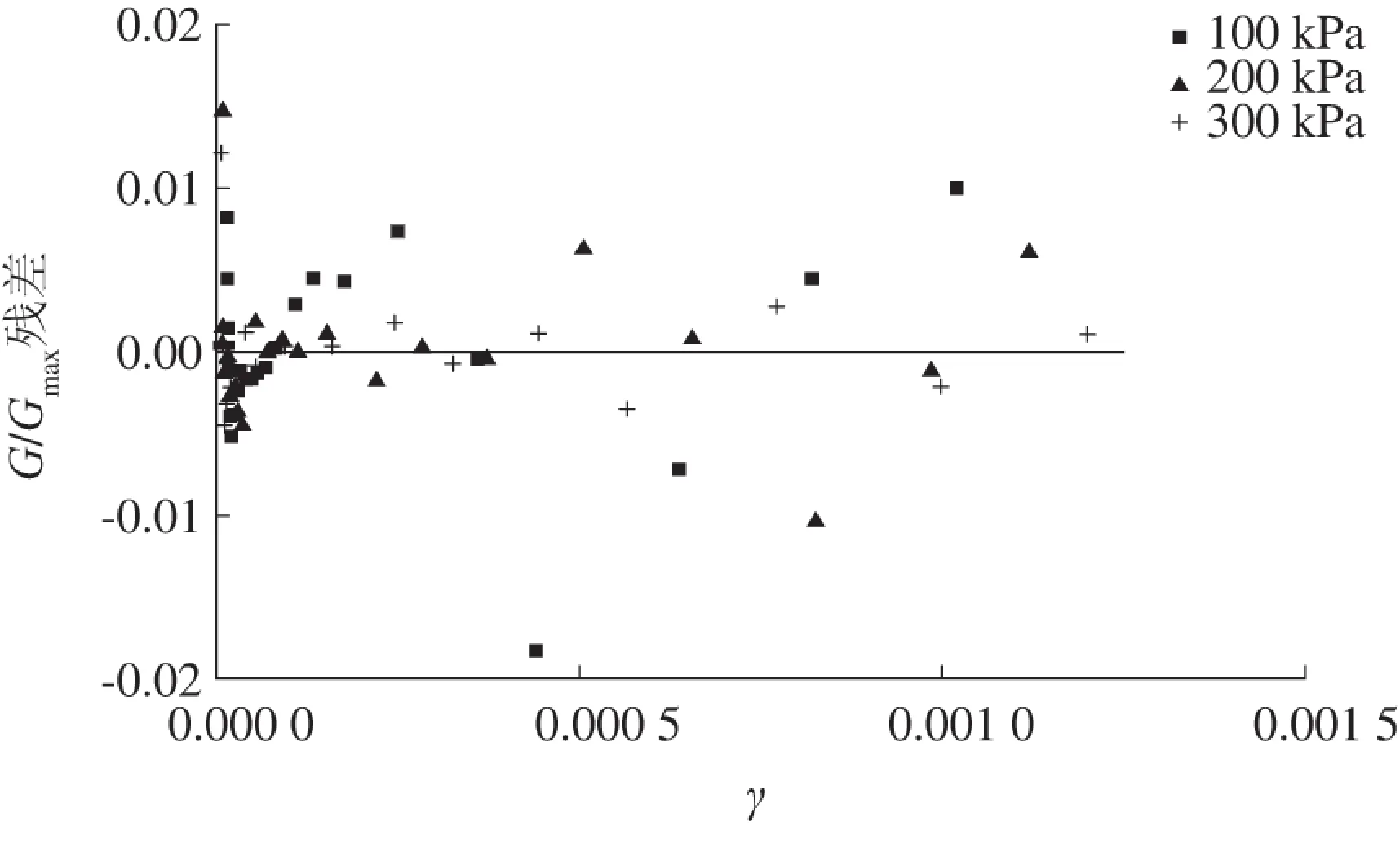
图10　Davidenkov模型动剪切模量比残差图

由图9—10可知：H-D模型中，残差随横坐标轴数值的变化而呈规律性变化，独立性差；除100 kPa围压的动剪切模量比的残差值在0值附近外，200、300 kPa围压的动剪切模量比的残差值只有少数几个在0值附近；Davidenkov模型的残差值在0值的上、下范围内随机分布，拟合程度较好。

从以上分析中可以看出，Davidenkov模型的拟合优度较好。产生这种结果的原因很多，笔者只说明其中两点：一是H-D模型的拟合参数与初始剪应变之间存在一定关系，该模型在本质上相当于是与土性相关的单参数模型，较简易；二是不同类型土的性质差异较大，受同一因素影响程度不同；无论条件是否相同，不同性质的土均表现出不同的动力特性，拟合模型很难适用于每一种情况。

4　结　语

H-D模型拟合参数较少，较简洁方便，但是拟合结果离散性较大，对于饱和粉土的拟合情况并不是很好。Davidenkov模型能够很好地反映动剪切模量比与动剪应变之间的变化规律，拟合较精确。选取不同模型进行拟合，可以为更好地描述土体的变化情况提供参考。本文可以得到以下结论：

1)不同围压下饱和粉土的动剪切模量随动剪应变的增大而减小，且在同一干密度、同一饱和度和同一固结比的条件下，当动剪应变一定时，动剪切模量随围压的增大而增大。但是随着动剪应变的增大，动剪切模量衰减的幅度逐渐减小。

2)不同围压的动剪切模量比同样符合随动剪应变增大而衰减的规律，且不同围压下的动剪切模量比差值不大；动剪切模量对最大动剪切模量具有较好的归一性。

3)H-D模型拟合曲线具有随拟合参数的增大而向右上方移动的趋势，在10-6左右应变范围内，试验点偏离曲线较远，相关程度低，变量间独立性差，模型不稳定。Davidenkov模型整体相关性高，回归曲线与试验点差值小，变量间相互独立，拟合优度较好。

3)在拟合优度分析中，评定标准与指标均有一定的局限性，要结合拟合实际，选择合适的模型和评判方法进行适宜分析，不能过分依赖指标值的大小。

[1]陈国兴,谢君斐,张克绪.土的动模量和阻尼比的经验估计[J].地震工程与工程振动,1995,15(1):73-84.

[2]李永强,景立平,梁海安,等.土体动剪切模量测定及非线性拟合方法研究[J].世界地震工程,2010,26(增刊1):247-252.

[3]Hardin B O,Drnevich V P.Shear modulus and damping of soils:measurement and parameter effects[J].Journal of Soil Mechanics and Foundation Division,1972,98(SM6):603-624.

[4]Martin P P,Seed H B.One-dimensional dynamic ground response analyses[J].Journal of the Geotechnical Division,1982,108(7):935-952.

[5]彭盛恩,王志佳,廖蔚茗,等.土的动剪切模量比和阻尼比的经验模型研究[J].地下空间与工程学报,2014,10(3):566-572.

[6]袁晓铭,孙锐,孙静,等.常规土类动剪切模量比和阻尼比试验研究[J].地震工程与工程振动,2000,20(4):133-139.

[7]黄志全,李日运.岩体力学参数试验数据可靠性检验分析[J].水文地质工程地质,2004,31(5):88-90.

[8]杨运清,杨汝康.非线性模型拟合结果的统计检验方法的适用性分析[J].西南民族学院学报：自然科学版,1993,19(3):308-311.

[9]王志佳.土及岩石动力学参数的统计与分析[D].成都：西南交通大学,2010.

[10]黄志全,李磊,贾景超,等.非饱和黄土动剪切模量和阻尼比共振柱试验研究[J].人民黄河,2015,46(5):69-72.

[11]湛川,李刚,刘莹莹.南水北调中线工程段弱膨胀土的动力学性质研究[J].华北水利水电学院学报,2013,34(3):70-73.

[12]南京水利科学研究院.土工试验方法标准(2007版)：GB/T 50123—1999[S].北京:中国标准出版社,1999.

(责任编辑：乔翠平)

Experimental Investigation on Dynamic Shear Modulus of Saturated Silt in Zhengzhou

HUANG Zhiquan， GUO Fangjie, JIA Jingchao， WU Chao， ZHANG Zhenhua

(North China University of Water Resources and Electric Power, Zhengzhou 450045, China)

The dynamic shear modulus of soil is an important parameter of dynamic characteristics of soil, the relationship between the dynamic shear modulus and the dynamic shear strain is one of the essential contents to research dynamic characteristics of soil. The relation model between the dynamic shear modulus and the dynamic shear strain can describe the dynamic relation between stress and strain. The soil sample in the experiment was selected from silt in Zhengzhou, and was prepared to remolding soil samples, the saturated silt was made a dynamic test under the undrained condition with GDS Resonant Column Apparatus, the dynamic shear modulus and the dynamic shear strain of soil sample in a small strain range of 10-6～10-3were measured. The relationship curve between the ratio of dynamic shear modulusG/Gmaxand the dynamic shear strainγwas conducted regression analysis with H-D fitting model and Davidenkov fitting model, and the result showed the better fitting model of saturated silt was Davidenkov model. The research results could provide a reference for the selection of the dynamic model of silt and seismic analysis.

saturated silt; dynamic shear modulus; resonant column;G/Gmax-γcurve; H-D model; Davidenkov model

2015-12-03

河南省科技创新人才计划(154100510006)；河南省重点科技攻关项目(152102210111)；新疆维吾尔自治区科技援疆项目资助(201491105)。

黄志全(1970—),男,河南潢川人,教授,博导,博士,主要从事岩土力学、边坡与滑坡工程方面的研究。E-mail:huangzhiquan@ncwu.edu.cn。

10.3969/j.issn.1002-5634.2016.01.012

TV16;TU411;P315.98

A

1002-5634(2016)01-0064-05