钢筋混凝土牛腿拉压杆模型受剪承载力分析

解伟， 王小兵， 李树山， 李红梅， 梅芃

(华北水利水电大学 土木与交通学院，河南 郑州 450045)



钢筋混凝土牛腿拉压杆模型受剪承载力分析

解伟， 王小兵， 李树山， 李红梅， 梅芃

(华北水利水电大学 土木与交通学院，河南 郑州 450045)

根据塑性下限原理，拉压杆模型只需满足平衡条件和屈服准则，因此多用于结构截面应变呈非线性分布的情形。本文介绍了利用拉压杆模型进行混凝土结构“D”区承载力设计的原理，对比分析了欧洲规范EN 1992-1-1和美国规范ACI 318-11及我国现行规范中关于拉压杆模型的计算方法。结合试验实例，利用拉压杆模型进行了钢筋混凝土牛腿的受剪承载力计算和分析，该方法的计算结果与试验结果的符合性较好。

牛腿；“D”区；拉压杆；受剪承载力

钢筋混凝土构件的几何或荷载不连续的区域，如集中力作用点、孔洞周围、框架节点、支托等，通常被称为“D”区。“D”表示不连续(Discontinue)、细部(Detail)或者扰乱(Disturb)。钢筋混凝土牛腿是一种典型的几何不连续结构。在抗剪计算中，这类构件在承载力极限状态下破坏截面的应力、应变不符合平截面假定，普通钢筋混凝土构件计算所依据的材料力学原理及模型就不再适用。我国现行规范(GB 50010—2010)采用三角桁架拉压杆简化模型作为单侧牛腿(“D”区)的计算模型。欧洲规范EN 1992-1-1[1]和美国规范ACI 318-11[2]也有关于“D”区的定义，并建议采用拉压杆的方法进行计算。本文首先介绍了欧洲规范和美国规范中拉压杆的计算步骤，并计算牛腿的受剪承载力，同时也根据我国现行规范对混凝土牛腿进行承载能力计算，最后对3种规范的计算值与试验值进行对比分析[3]。

1　拉压杆模型介绍

拉压杆模型是基于塑性下限原理在实际设计计算中的一种特定应用，适用于截面应变为非线性分布的情形。牛腿是出现非线性应变分布的典型结构，其拉压杆模型如图1所示,其中V表示施加在牛腿上的竖向荷载。圣维南原理也指出轴向荷载引起的压力和挠度接近线性分布，逼近于构件上的最大值，远离不连续性，因此不连续假设用来扩充来自荷载或几何发生突变的部分。拉压杆模型的“D”区须保持所施加的荷载与反作用力的平衡，以及每一节点和每一杆件的自平衡。因此一个符合条件的拉压杆模型，只需满足平衡条件和屈服准则，一般不考虑固体力学中的应变协调[4-5]。

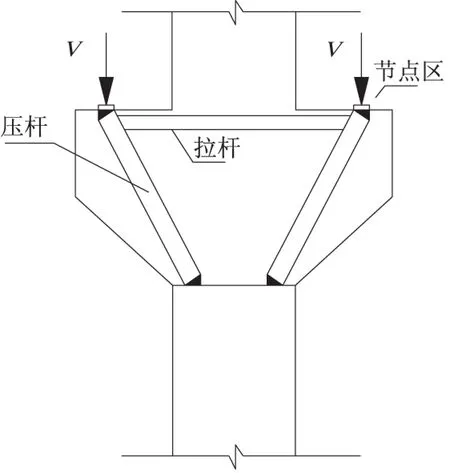
图1　牛腿的拉压杆模型

拉压杆模型是由拉杆区、压杆区和节点区组成。拉杆代表受拉钢筋的作用区域。由于混凝土的抗拉能力很弱，在设计计算过程中不考虑拉杆周围所包裹的混凝土的受拉作用。压杆主要代表受压区混凝土的作用。压杆是拉压杆模型中一种理想化的受压构件，按照力流的大致走向在实际处理中可以简化为等截面的压杆，如图1所示。节点区是拉杆和压杆集中力轴线相交接的点所在的区域,由于拉杆和压杆一般不在一条直线上，节点区至少应作用3个力，以满足平衡准则所达到的条件。节点类型如图2所示,其中C代表压力，T代表拉力。

图2　常见的节点类型

2　利用拉压杆模型计算牛腿受剪承载力

2.1利用欧洲规范EN 1992-1-1的拉压杆模型进行计算

2.1.1压杆的承载力计算

在压杆设计中，一般压杆的实际形状为瓶形压杆，但通常都被简化为等截面的压缩构件,有时候也被简化为均匀的变截面压缩构件。欧洲规范EN 1992-1-1给出了抗压强度与主拉应变之间的关系，根据研究成果给出了两种受力状态的简化压应力极限计算公式：

1)横向无拉应力或者有压应力时，

σ=fcd;

(1)

2)横向有拉应力且允许开裂时，

σ=0.6vfcd。

(2)

式中:σ为混凝土的正应力；fcd为混凝土的抗压强度设计值，fcd=αccfck/γc;αcc为荷载对抗压强度的不利影响系数，欧洲规范推荐取值为0.8～1.0，这里式(1)中取为0.85,式(2)中取为1.0;γc为混凝土的分项安全系数，在持久状态下取值1.5，偶然状态下取值1.2;fck为混凝土抗压强度标准值;v为剪力作用下混凝土开裂后的强度折减系数,欧洲规范推荐v=1-fck/250。

2.1.2节点区的承载能力

集中力作用点和支座施加荷载处有拉杆、压杆及荷载的作用。节点的设计方法不同,拉杆和压杆力传递的方式也不同，欧洲规范EN 1992-1-1规定了3种不同类型的集中节点，给出了极限应力σmax计算方法，分别如下：

1)节点区没有锚固拉杆的节点，

σmax=k1vfcd;

(3)

2)一个方向有锚固拉杆的节点，

σmax=k2vfcd;

(4)

3)多个方向有锚固拉杆的节点，

σmax=k3vfcd。

(5)

欧洲规范推荐：k1=1.0，k2=0.85，k3=0.85。当fcd至少满足下面一个条件时，节点处的抗压强度可以提高10%：①节点处于三向受压状态；②节点处压杆和拉杆的夹角大于等于55°；③作用于支座的荷载应力均匀分布或者节点处有足够的支撑和摩擦约束。

2.1.3拉杆的承载力计算

拉杆是指由钢筋提供拉力，而不考虑钢筋周围混凝土的抗拉作用。钢筋的面积计算公式为

As=F/(fy/γs)。

(6)

式中：As为拉杆钢筋的面积；F为构件所承受的最大外荷载；fy为钢筋屈服强度；γs为钢筋分项系数，欧洲规范推荐该系数取值1.15。在设计过程中应保证该拉杆的实际应力小于钢筋的设计屈服强度。

2.2利用美国规范ACI 318-11的拉压杆模型进行计算

2.2.1压杆的承载力计算

美国规范ACI 318-11规定压杆的承载能力按下式计算：

Fns=fceAcs。

(7)

式中：Fns为压杆的轴向承载力；Acs为压杆端部的承载截面面积；fce为混凝土的有效抗压强度，fce取下列两式计算结果的较小值。

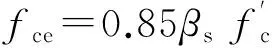
(8)

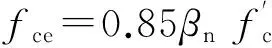
(9)

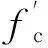
2.2.2节点区的承载力计算

节点区是拉压杆模型中又一处容易发生破坏的区域。文献[4]指出了节点区的设计与支撑于该节点上的混凝土压杆的强度、锚固于该节点区域的钢筋拉杆之间有着密切的联系。因为计算者所选择的拉压杆模型的节点设计方法会影响拉压杆模型中力的传递。因此拉压杆模型中压杆与拉杆的尺寸拟定与节点区域的验算是一个反复的设计过程，一项改变会影响其他两项，最终的设计目的是使拉杆、压杆与节点均满足设计要求。美国规范ACI 318-11推荐采用下列公式计算：

Fnn=fceAnz。

(10)

式中：Fnn为节点区的最大承载力；Anz为节点区的表面积；fce按公式(9)取值。节点区的表面积可以近似简化为压杆节点处的横截面面积。节点区的形式如图3所示，其中W表示节点区不同边的长度，l表示拉杆钢筋伸入节点区的长度。

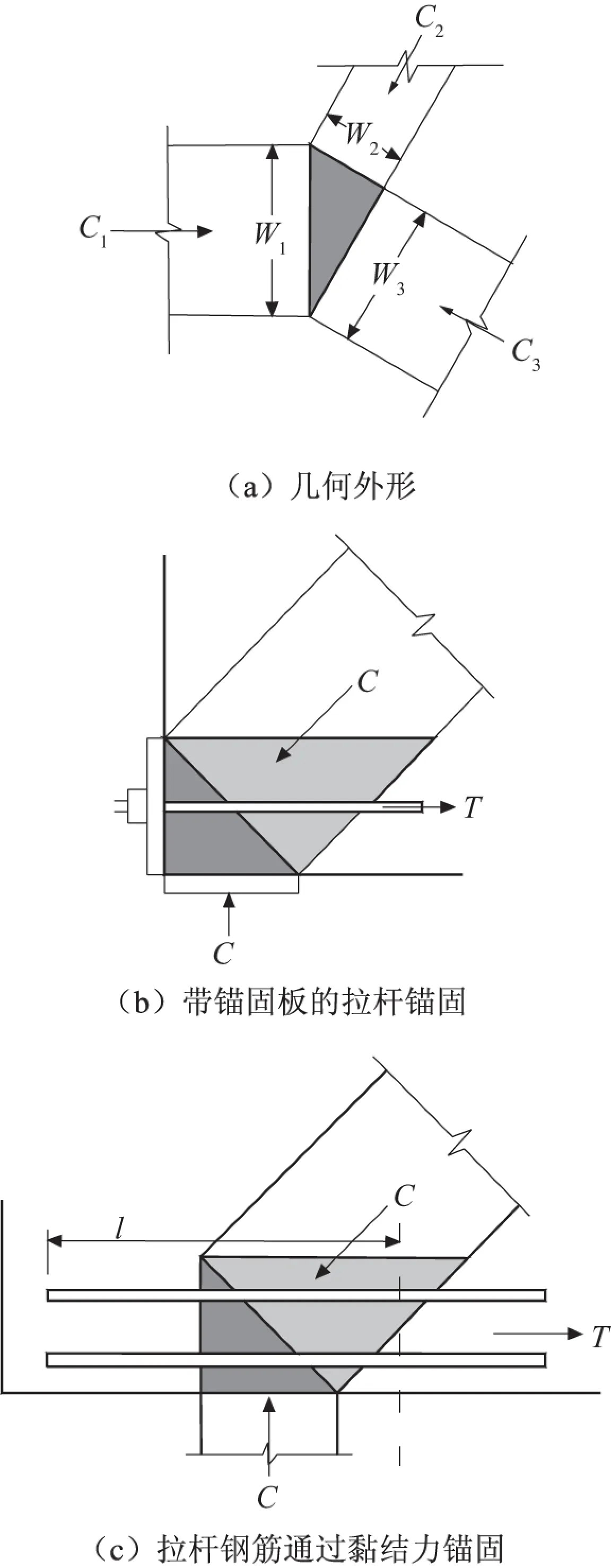
图3　节点区示意图

2.2.3拉杆的承载力计算

拉压杆模型中的拉杆是由受拉钢筋及其周围的混凝土组成，实际计算过程中由于混凝土的抗拉能力很小，故忽略混凝土的抗拉作用。狭义拉杆就是由受拉钢筋代替。美国规范ACI 318-11采用下列公式计算拉杆的最大承载力：

Fnt=Atsfy+Atp(fse+Δfp)。

(11)

式中:Fnt为拉杆的最大承载力;Ats为拉杆钢筋的面积;fy为拉杆钢筋的强度;如果钢筋为预应力钢筋，Atp为预应力钢筋的面积,对于非预应力构件Atp为零；fse为预应力状态下钢筋的强度值；Δfp为考虑黏结性时的钢筋附加强度值,对于有黏结的预应力钢筋，Δfp=420 MPa，采用无黏结预应力钢筋时，Δfp=70 MPa，其余工况根据实际试验数据分析。拉杆的设计宽度可以根据钢筋的布置情况来确定。

2.3平衡准则及压杆截面尺寸的选取

拉压杆模型是由桁架理论演化而来的一种实用模型，同样也要满足力的平衡准则。即在节点区由纵向钢筋构成的拉杆的水平向的拉力T、混凝土受压区压杆产生的压力F及外荷载的竖向作用力V满足平衡条件。文献[5]推荐V=Fsinθ，T=Vcotθ。其中θ为拉杆与压杆的夹角。以力学平衡条件为基础，根据规范计算出的理论值反算出构件所能承担的荷载值，进而与试验值进行对比。

压杆的瓶形截面在被简化为等截面压杆后，文献[6]推荐压杆截面宽度ws的计算公式为

ws={1.8wtcosθ+[(lP)P+(lP)E]sinθ}/2。

(12)

因压杆宽度的取值至今没有统一的选取标准，考虑到计算的简便性及有效性，在本文中压杆截面宽度ws可采用下列公式计算：

ws={1.8wtcosθ+2(lP)Psinθ}/2。

(13)

θ取值也没有完全统一的标准[6-8]，本文按照文献[6]推荐的公式计算，

arctanθ=jd/a≥25°,

(14)

jd=h0-0.9wt。

(15)

式中：wt为节点区的高度；(lP)E为荷载作用的宽度；(lP)P为支座处的作用宽度，本文近似取垫板的宽度76.2 mm；h0为截面的有效高度；jd为压杆的竖直高度；a为集中荷载到支座处的垂直距离。

2.4我国现行规范有关牛腿的规定

我国现行的《混凝土结构设计规范》(GB 50010—2010)[9]采用三角桁架模型[10](其受力分析特点与拉压杆模型本质上相同)进行受力分析。对牛腿裂缝的控制要求采用下式计算：

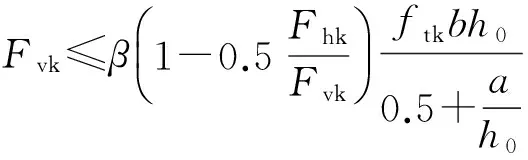
(16)

式中：Fvk为作用于牛腿顶部按荷载效应标准组合计算的竖向值；Fhk为作用于牛腿顶部按荷载效应标准组合计算的水平拉力值；β为裂缝控制系数，对于支承吊车梁的牛腿,β取0.65，其他牛腿,β取0.8；a为竖向力作用点至下柱边缘的水平距离，应考虑安装偏差(20 mm)，当考虑安装偏差后的竖向力的作用点仍位于下柱截面以内时取0 mm；ftk为混凝土的轴心抗拉强度标准值；b为牛腿宽度；h0为牛腿与下柱交接处的垂直截面有效高度。

承受竖向力所需的受拉钢筋截面积和承受水平拉力所需的锚筋截面面积所组成的纵向受力钢筋的总截面面积As有如下规定：

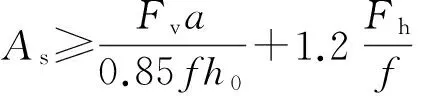
(17)

式中：Fv为作用在牛腿顶部的竖向力设计值；Fh为作用在牛腿顶部的水平拉力设计值。

我国规范从裂缝控制和承载力两个方面进行牛腿的抗剪承载力分析。国内现行规范和欧美规范在基本原理上是相同的。我国现行规范主要从设计调整牛腿的尺寸来控制裂缝的发生，欧美规范主要从应力是否达到允许应力来进行设计。

3　理论计算结果与试验结果对比

根据上述规范推荐的计算方法，文献[11]认为剪跨比a/h0=0.3的牛腿更加接近于桁架模型，其拉压杆模型如图4所示。其参数V表示竖向荷载；θ为拉杆与斜压杆之间的夹角；wt为节点区的高度；ws为压杆的宽度；h为压杆的竖向总高度；h0为截面的有效高度；γ为保证系数。

对剪跨比a/h0=0.3的牛腿试件采用2种规范

进行受剪承载力计算，并与试验结果[12]进行对比分析。文献[12]中牛腿试件根部截面高h=350 mm,端高h1=200 mm,牛腿试件采用3种配合比，每组2个试件。每个试件配有4φ12 mm的纵向受拉钢筋和φ6@100 mm的箍筋。受拉钢筋是强度为474 MPa的高强钢筋。由于试验主要考虑剪跨比a/h0=0.3，按《混凝土结构设计规范》不配置弯起钢筋。试验中加载处垫板的截面尺寸取76.2 mm×260.0 mm。在万能试验机上采用对称的双牛腿进行加载，主要考虑开裂荷载和极限荷载。各级荷载作用下的裂缝宽度由读数显微镜测出。

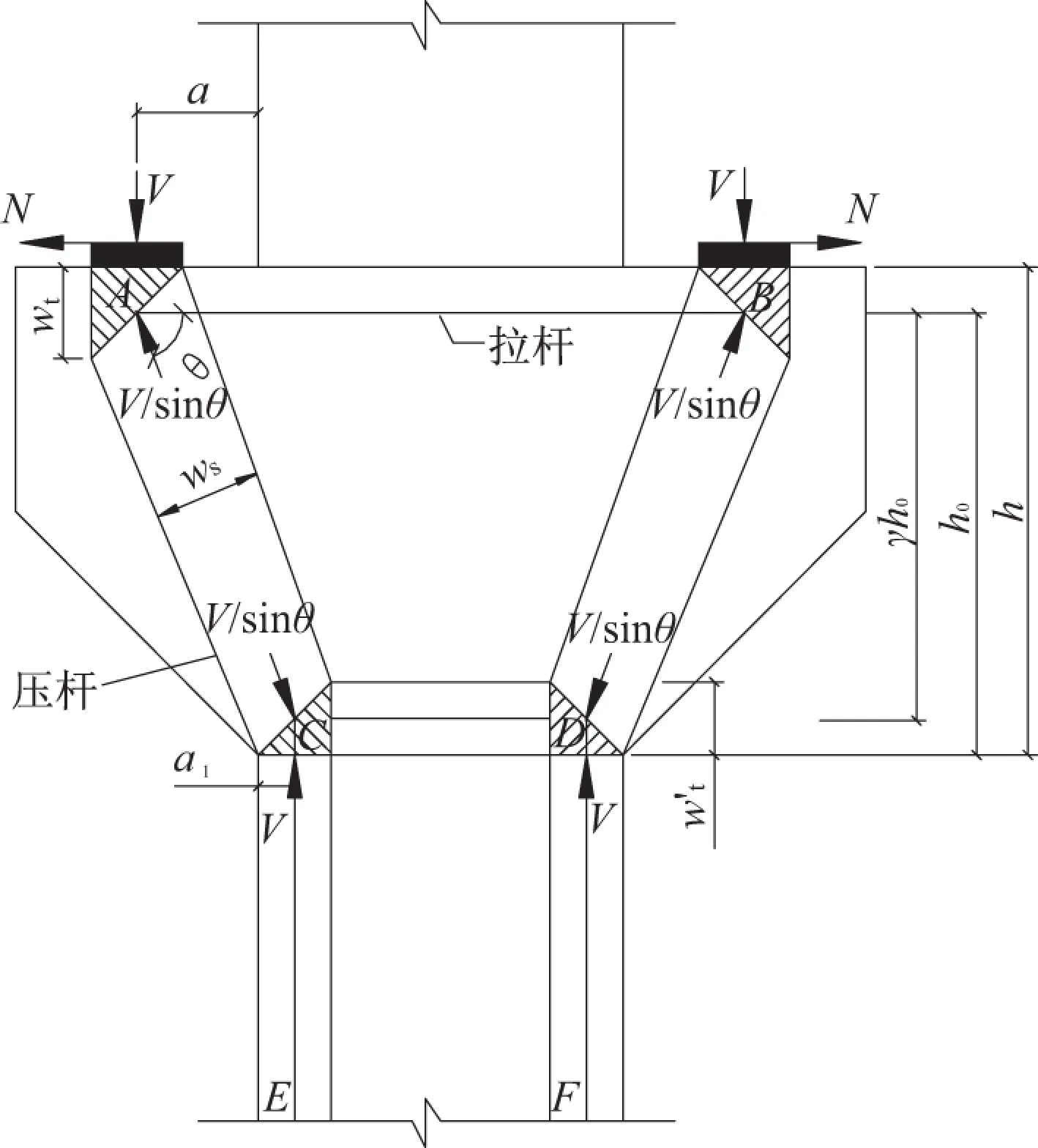
图4　牛腿的拉压杆模型示意图

牛腿受剪承载力分别按欧洲、美国及我国的现行规范进行计算，可根据欧美两种规范计算出的最大应力及作用面积进一步推算出节点区、压杆区及拉杆区所能承受的最大荷载。本文分别采用欧洲规范、美国规范及我国现行规范，结合异性柱[13]的结构设计，计算牛腿压杆区和节点区的最大承载力。通过力的平衡及合成原理进而反算出作用于试验牛腿的最大荷载，结果见表1。

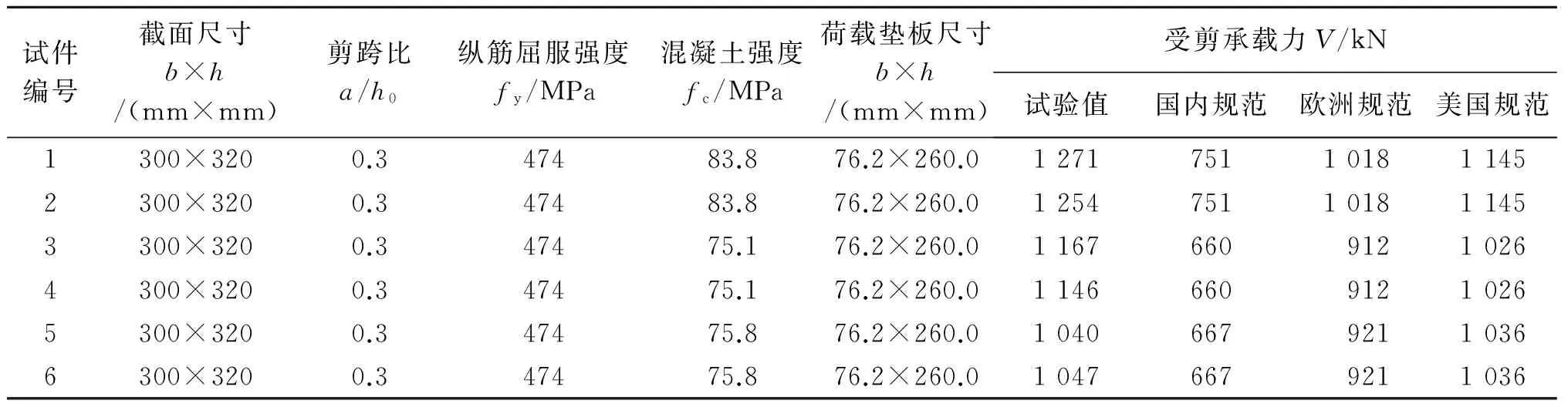
表1　牛腿受剪承载力试验值与理论计算值对比

由表1可以看出:国内现行规范的计算值小于欧洲规范和美国规范的计算值，国内现行规范的计算值比试验值小，而欧美规范与试验结果较为接近。这也说明了利用中国、美国、欧洲的规范进行计算，其结果都能满足牛腿的受剪承载能力要求。根据3个规范进行计算，牛腿都处于安全可靠的状态。

4　结　语

采用拉压杆模型进行计算时，影响牛腿斜截面承载力的主要参数有混凝土的强度、钢筋的强度及用量．另外，拉杆与压杆之间的角度、压杆尺寸和节点尺寸的选取对计算结果会有较大的影响。通过采用国内现行规范、欧洲规范EN 1992-1-1和美国规范ACI 318-11对试验牛腿的验算可以看出，国内现行规范对拉压杆模型的计算结果更偏于保守，而美国规范与欧洲规范的计算值与试验实测值更为接近，但都处于安全可靠的范围之内。

[1]European Committee for Standardization.Design of Concrete Structures:EN 1992-1-1[S].London:[s.n.],2004.

[2]American Concrete Institute.Building Code Requirements for Structural Concrete(ACI 318-11) and Commentary[M].Farmington Hills：[s.n.]，2011.

[3]李树山，高丹盈，解伟.钢筋混凝土牛腿结构拉压杆模型[J].土木建筑与环境工程，2013,35(增刊1)：36-39.

[4]夏飞，张春华.欧洲规范拉-压杆模型设计分析[J].中外公路，2015,35(3)：163-169.

[5]熊进刚，付国平.钢筋混凝土无腹筋短梁受剪承载力计算的软化桁架模型[J].南昌大学学报(工学版)，2004，26(1)：49-53.

[6]Yang K H,Ashour A F.Strut-and-Tie model based on crack band theory for deep beams[J].ACI Journal of Structural Engineering,2011，137(10):1030-1038.

[7]林波.拉压杆模型及其在预应力混凝土梁桥D区设计中的应用[D].南京：东南大学，2011.

[8]刘立渠，王娟娟，韩继云，等.钢筋混凝土简支深梁静力性能试验研究及拉压杆模型分析[J].建筑结构学报，2013,10：137-143.

[9]中华人民共和国住房和城乡建设部.混凝土结构设计规范:GB 50010—2010[S].北京：中国建筑工业出版社，2010：129-131.

[10]河海大学，武汉大学，大连理工大学，等.水工钢筋混凝土结构学[M].4版.北京：中国水利水电出版社，2009：272-281.

[11]白俊光，魏坚政，后广斌.水工钢筋混凝土结构设计技术研究[M].北京：中国水利水电出版社，2009：264-294.

[12]Yang J M,Lee J H,Yoon Y S,et al.Influence of steel fibers and headed bars on the serviceability of high-strength concrete corbels[J].ACI Journal of Structural Engineering,2012，138(1):123-129.

[13]陈爱玖，张利永，刘洪波.异形柱的结构设计[J].华北水利水电学院学报，2004，25(1)：4-7.

(责任编辑：陈海涛)

Analysis on Shear Capacity of Reinforced Concrete Corbel by Utilizing the Strut-and-tie Model

XIE Wei, WANG Xiaobing, LI Shushan, LI Hongmei, MEI Peng

(North China University of Water Resource and Electric Power, Zhengzhou 450045, China)

According to the principle of plastic lower limit, the strut-and-tie model only needs to satisfy the equilibrium conditions and the yield criterion, so it is mostly used in the cases that the nonlinear strain distribution of the structure section. In the article, it was introduced that the design principles of the bearing capacity of ‘D’ district in a concrete structure by using the strut-and-tie model, the calculation methods of the strut-and-tie model in the European standard (EN 1992-1-1) and American standard (ACI 318-11) were comparatively analyzed. Combined with experimental instances, the shear capacity of reinforced concrete corbel was calculated and analyzed by using the strut-and-tie model, and the calculation results were good agreement with the experimental results.

corbel; “D”district; strut-and-tie； shear capacity

2015-11-02

国家自然科学基金资助项目(U1404526);郑州科技领军人才培育计划(112PLJRC354)；河南省科技攻关项目(142102310536)；水利部堤防工程中心开放基金(201401)；郑州市科技攻关项目(131PPTGG410-3)。

解伟(1958—),男,河南开封人,教授,博导,博士,主要从事水工结构及混凝土材料方面的研究。E-mail:xwei@ncwu.edu.cn。

10.3969/j.issn.1002-5634.2016.01.010

TV332;TU375

A

1002-5634(2016)01-0055-05