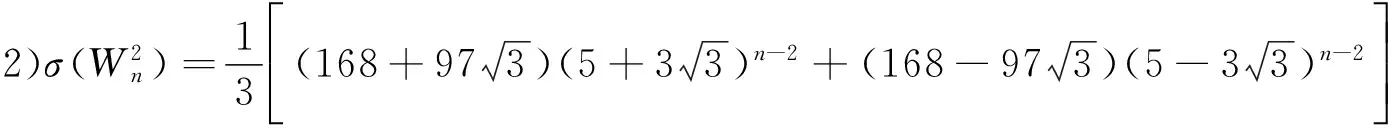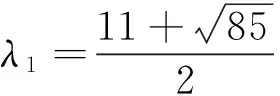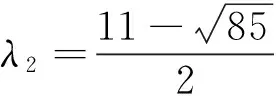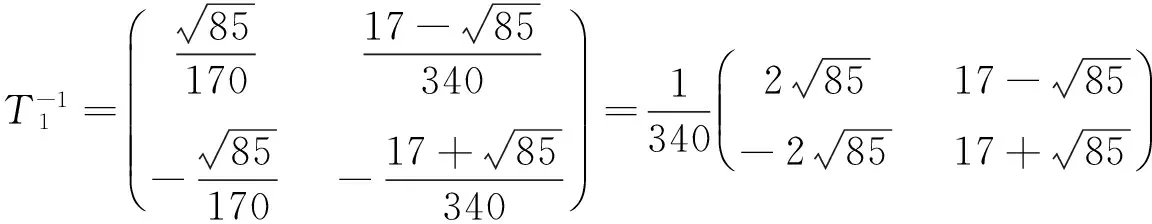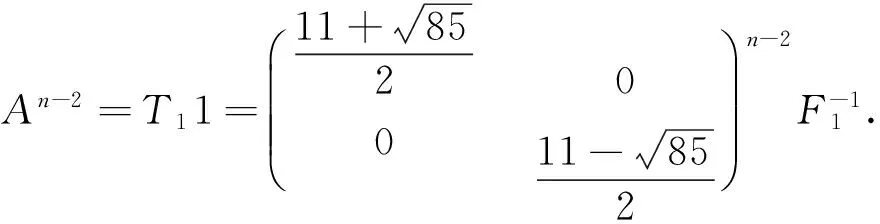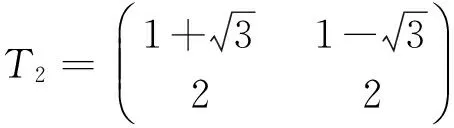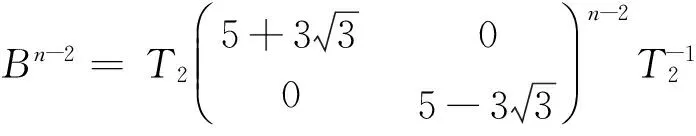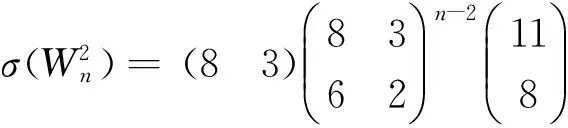五边形链的Merrifield-Simmons指标
刘睿琳,田双亮,田文文
(西北民族大学 数学与计算机科学学院,甘肃 兰州 730030)
五边形链的Merrifield-Simmons指标
刘睿琳,田双亮*,田文文
(西北民族大学 数学与计算机科学学院,甘肃 兰州 730030)

五边形链;Merrifield-Simmons指标;递推公式
0 引言
Merrifield-Simmons指标是在1989年由美国化学家Merrifield和Simmons在文献[1]中引入的化学拓扑指标,它表示图G中所有独立集的数目,记为σ(G).该指标与物质的沸点有着密切的联系,且有着较为广泛的应用,相关的应用参见文献[2,3].文献[4]中研究了五角链关于独立集数的极端情形,并得出了相应的极图.文献[5,6]中研究了四角链及五边形链的Hosoya指标.文献[7]关于最大和最小的Merrifield-Simmons指标给出了一个很好的综述.文中Fn表示第n个Fibonacci数,即满足Fn=Fn-1+Fn-2,n≥2,且F0=0,F1=1.本文通过n个五边形序列在不同构联接位下构造了两类特殊的五边形链,并且研究了这两类五边形链的Merrifield-Simmons指标,给出了具体的表达式.文中未加说明的符号及术语参见文献[8].
设Q1,Q2,…,Qn为n个五边形构成的五边形序列.记Wn为五边形链,如果满足:
1)对任意的1≤s 2)每个正方形与割边的顶点都为3度顶点. 用Φn表示含有n个五边形构成的五边形链的全体.设Wn∈Φn,则五边形链Wn(n≥2),可由Wn-1再联接一个五边形得到,而每条链中的五边形都有四个可联接位,其中与接点距离相等的两个可联接位是同构的,所以只有两种非同构的联接方式:Wn-1→[Wn-1]k=Wn,其中k=1、2,分别称为1-位联接和2-位联接,如图1所示. 图1 两种联接方式 图2 五边形链和 在证明主要结论之前,先给出几个相关引理如下. 引理1[2]设G是一个简单图,对任意的υ∈V(G),有σ(G)=σ(G-υ)+σ(G-NG[υ]). 引理3[2]对于n阶的路Pn,有σ(Pn)=Fn+2. 引理4[2]对于n阶的圈Cn,有σ(Cn)=Fn+1+Fn-1. 定理1对任意的正整数n≥2,有 证明1) 如图2所示,根据引理1、引理2和引理3可得 2)如图2所示,根据引理1、引理2和引理3可得 定理2对任意的正整数n≥2,有 [1] Merrifield R E,Simmons H E.Topological Methods in Chemistry[M].New York:Wiley,1989. [2] Gutman I,Polansky O E.Mathematical Concepts in Organic Chemistry[M].Berlin:Sprin-ger,1986. [3] Gutman I,Cyvin S J.Introduction to the Theory of Benzenoid Hydrocarbons[M].Berlin:Springer,1989. [4] 曹月芬.五角链关于独立集数的极端情形[J].集美大学学报,2010,15(4):304-307. [5] 田文文,田双亮.四角链的Hosoya指标[J].苏州科技学院学报(自然科学版),2014,31(1):34-38. [6] 田文文,杨斐,田双亮.五边形链的Hosoya指标[J].重庆工商大学学报(自然科学版),2013,30(9):29-33. [7] Wagner S,Gutman I.Maxima and minima of the Hosoya Index and the Merrifield-Simmons index[J].Acta Appl Math,2010,112:323-346. [8] Bondy J A,Murty U S R.Graph theory with applications[M].New York:The Macmillan Press,1976. The Merrifield-SimmonsIndex of Pentagonal Chains LIU Rui-lin1,TIAN Shuang-liang,TIAN Wen-wen (Mathematics and Computer Science College,Northwest University for Nationalities,Lanzhou 730030, China) Pentagonal chains;Merrifield-Simmons index;Recurrence formula 2016-04-02 国家民委科研项目(14XBZ018);甘肃省自然科学基金(145RJZA158);西北民族大学中央高校基本科研业务费专项资金资助研究生项目(Yxm2015182). * 刘睿琳(1993— ),女,甘肃永靖人,硕士研究生,主要从事组合数学与图论方面的研究. O157.5 A 1009-2102(2016)02-0001-05


1 主要结论及其证明
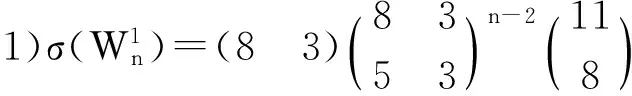

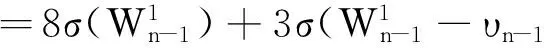
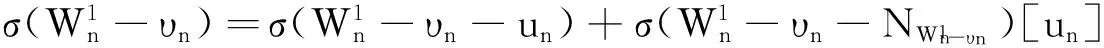
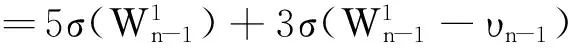



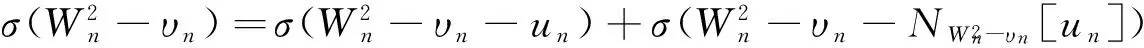

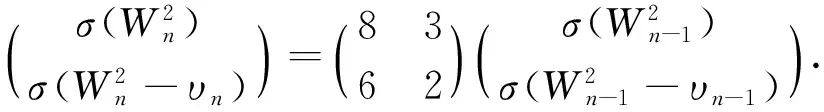


2 进一步的结果