聚能射流侵彻土壤/混凝土复合目标理论研究

肖强强，刘荣忠，冯成良，黄正祥，魏许昌

(1.重庆红宇精密工业有限责任公司，重庆 璧山　4027602.南京理工大学 机械工程学院，南京　210094)



聚能射流侵彻土壤/混凝土复合目标理论研究

肖强强1,2，刘荣忠2，冯成良1，黄正祥2，魏许昌1

(1.重庆红宇精密工业有限责任公司，重庆 璧山4027602.南京理工大学 机械工程学院，南京210094)

为了研究聚能射流对土壤/混凝土复合目标的侵彻效应，分析土壤/混凝土复合目标在聚能射流侵彻下的响应特性，通过考虑聚能射流侵彻下塑性波在靶板中的传播和衰减，以及在土壤/混凝土界面的反射和透射，分析了反射波和透射波作用下射流对土壤和混凝土的侵彻过程，研究土壤/混凝土复合目标界面效应对聚能射流侵彻的影响，建立了聚能射流侵彻土壤/混凝土复合目标的理论模型。对聚能射流侵彻单一混凝土靶和土壤/混凝土复合靶进行对比试验发现，由于反射波和透射波的影响，聚能射流对土壤/混凝土复合靶的侵彻深度反而低于对单一混凝土靶的侵彻深度。在反射波和透射波的作用下射流的侵彻速度下降，导致了对土壤/混凝土复合靶侵彻深度的降低，试验结果与理论分析一致。

聚能装药；土壤/混凝土复合目标；塑性波；侵彻深度；对比试验

由于岩土类介质原材料丰富、防护性能良好，被广泛应用于军事防护工程，通过构筑几米甚至几十米厚的防护结构，达到保护人员和设备的目的，尤其是采用双层或多层岩土介质结构，利用相邻介质间的界面效应提高抗弹能力，达到增强工事、掩体等目标防护性能的目的，其中以土壤/混凝土复合目标结构应用较多。

国内外学者针对战斗部对岩土类目标的侵彻能力进行了大量研究，HUERTA等[1]根据数值计算结果设计了Φ700 mm聚能装药战斗部，用于对付岩石和混凝土目标。LUK等[2-3]采用空腔膨胀理论分别对弹丸侵彻钢筋混凝土和土壤进行了分析。FORRESTAL等[3-4]通过试验验证了上述理论模型。VOOREN等[5]对弹丸侵彻沙土过程进行了试验研究。SHI等[6]则采用空腔膨胀理论建立了弹丸侵彻干沙的理论模型，并进行了试验研究。CHURCH等[7]结合试验进行了聚能装药侵彻混凝土、沙、土壤及多层介质目标的数值仿真。蒋志刚等[8]对弹丸侵彻钢管约束混凝土进行了仿真计算。张兆军等[9]分析了弹丸贯穿不同种类粗骨料混凝土后的剩余速度。纪冲等[10]则弹丸贯穿有限厚混凝土靶板后的背面崩落情况进行了研究。对于土壤/混凝土复合目标，蔺建勋等[11-12]基于空腔膨胀理论，通过考虑层间介质的力学响应，建立了弹丸侵彻土壤/混凝土复合目标的理论模型，周玉兵[13]对弹丸斜侵彻土壤/混凝土复合目标进行了仿真分析，由于在土壤与混凝土交界处存在界面效应，致使斜侵彻时弹道方向发生改变，弹丸侵彻威力急剧下降。

尽管国内外对弹丸侵彻岩土类目标进行了大量研究，但对聚能射流侵彻土壤/混凝土复合目标方面的研究则甚少见诸报道。本文考虑到聚能射流侵彻时在靶板中形成的塑性波，通过分析塑性波在靶板中的传播和衰减，以及在土壤/混凝土界面的反射和透射，研究界面效应对聚能射流侵彻土壤/混凝土复合目标的影响，建立了聚能射流侵彻土壤/混凝土复合目标理论模型。采用聚能射流侵彻单一混凝土靶和土壤/混凝土复合靶对比试验，对上述模型进行了验证。

1　聚能装药侵彻土壤/混凝土复合目标理论模型

材料中的应力超过其弹性极限时，就会出现塑性变形，而当半无限体中的塑性波横向应变为零时，就为单轴应变状态[14]。聚能射流侵彻靶板时，产生的应力远大于材料的弹性极限，在侵彻点周围形成塑性区，随着侵彻过程的进行，塑性波向前传播并不断衰减。当塑性波到达土壤/混凝土界面时发生反射和透射，致使土壤和混凝土的应力状态发生改变，进而影响射流对土壤/混凝土复合目标的侵彻。

为考虑塑性波的作用，分析界面效应对侵彻过程的影响，对聚能射流侵彻土壤/混凝土复合目标作出如下假设：

(1)土壤、混凝土为均匀各向同性、理想弹塑性材料；

(2)不考虑靶板的边界效应，土壤为有限厚的无径向边界靶板，混凝土靶板为半无限厚靶板，即不考虑卸载波的作用；

(3)塑性波传播时横向应变为零，材料处于单轴应变状态；

(4)通常在工程计算中介质的应力波峰值衰减可采用指数函数和幂函数形式来描述，本文按照指数形式衰减描述其过程，衰减系数为与土壤、混凝土特性有关的常数。

1.1塑性波在靶板中的传播和衰减

聚能射流侵彻靶板时，弹靶界面的压力可由Bernoulli方程给出

(1)

式中:p0为弹靶界面的初始压力，ρj、vj分别为射流的密度和着靶速度，u为射流侵彻速度。

该初始压力以塑性波的形式向四周传播，根据假设塑性波传播时按照指数形式衰减，则传播距离为x时，塑性波的强度衰减为

px=p0e-γx

(2)

式中，px为塑性波传播距离x时的波强度，γ为塑性波在靶板中传播时的衰减系数。

随着塑性波的衰减，当塑性波的强度低于靶板的动态屈服强度Rt时，此时塑性波转变为弹性波继续传播，由于射流侵彻靶板时产生的压力远大于靶板的动态屈服强度，弹性区域对侵彻过程的影响较小，本文仅考虑塑性区域的作用，不再对弹性区域进行计算。

图1为射流侵彻靶板及塑性波传播过程示意图，射流侵彻到O点时，由O点产生起始扰动并形成塑性区域，到起始扰动点的距离I可由式(3)求解得到

(3)

图1　射流侵彻和塑性波传播示意图Fig.1　The illustration of jet penetration and plastic wave propagation

传播的时间Δt为

(4)

式中:Cp为塑性波的传播速度。此时弹靶界面到O点的距离ΔP为

ΔP=u·Δt

(5)

联立式(4)和(5)并消去Δt，则得到在侵彻轴线上弹塑性边界到起始扰动点与其到弹靶界面的距离关系式为

(6)

对于侵彻轴线上的S点，其到弹靶界面的距离为s，同理可得S点的起始扰动位置，并由式(2)得到S点的压力为

(7)

式中:γ为波在靶板中的衰减系数。而S点的质点速度vS可由Bernoulli方程得到其控制方程为

(8)

式中:ρt为靶板密度。

现考虑弹塑性边界处，其质点速度远小于射流的侵彻速度，而靶板的压力为其动态屈服强度Rt，因此将式(1)代入式(8)可得

(9)

此式即为Alekseevskii-Tate (A-T)方程。而在弹靶界面处由于pS=p0，可以由式(8)得到vS=u，即弹靶界面处靶板的质点速度等于射流的侵彻速度。

根据上述分析，在塑性区域内的侵彻轴线上，距弹靶界面不同位置处的压力和质点速度则可由式(7)和式(8)分别求得。

1.2界面效应对聚能射流侵彻过程的影响

塑性波到达土壤/混凝土界面时，形成反射波和透射波，并分别向土壤和混凝土传播，改变了射流稳定侵彻时靶板的应力状态，对聚能射流侵彻土壤/混凝土复合目标产生影响，如图2所示。

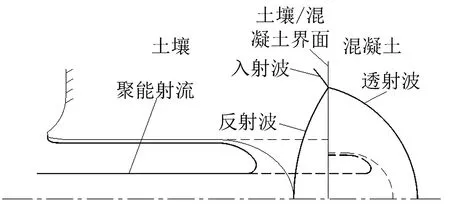
图2　界面效应影响Fig.2　The influence ofsoil/concrete interface

入射波的强度pI及质点速度vI，可根据土壤/混凝土界面到弹靶界面的距离由式(7)和式(8)计算得到，则由波的反射和透射理论，可以分别得到反射波和透射波的压力、质点速度与入射波的关系为

(10a)

(10b)

(11a)

(11b)

式中:ρS、CS为土壤的密度和塑性波速度，ρC、CC为混凝土的密度和塑性波速度，pR、vR为反射波的压力和质点速度，pT、vT为透射波的压力和质点速度。上式中令pI=pS、vI=vS，则可得到土壤/混凝土界面与弹靶界面相距s时，反射波和透射波的相关参数。

反射波和透射波传播时，仍按照指数形式衰减进行计算，则当S点的反射波到达弹靶界面时，其压力pSR和质点速度vSR分别为

(12a)

(12b)

式中:γS为波在土壤中的衰减系数。

由于反射波的影响，聚能射流侵彻土壤/混凝土复合目标时，弹靶界面与反射波相遇，则相当于土壤具有初始压力pSR、初始速度vSR，即射流相对于靶板的速度为(vj-vSR)，由Bernoulli方程可以得到

(13)

式中:uSr为土壤弹靶界面相对靶板的运动速度。在反射波作用下聚能射流的实际侵彻速度uSR即为

uSR=uSr+vSR

(14)

当该现象引起的扰动在土壤/混凝土界面反射后，又会重新对聚能射流侵彻过程产生作用，致使反射波的作用不断增强，同时射流的侵彻速度也是不断变化的。

透射波对聚能射流侵彻过程同样产生作用，混凝土中距土壤/混凝土界面为c处的透射波强度pCT和质点速度vCT分别为

pCT=pTe-γCc

(15a)

(15b)

式中:γC为波在混凝土中的衰减系数。

此时聚能射流侵彻混凝土的控制方程为

(16)

及透射波作用下聚能射流的实际侵彻速度uCR为

uCR=uCr+vCT

(17)

式中:uCr为混凝土弹靶界面相对靶板的运动速度。

注意到土壤的波阻抗要低于混凝土，因此土壤中反射波的质点速度与射流侵彻速度方向相反，即vSR<0，并且由于反射波强度pSR远大于土壤的侵彻阻抗，由式(13)和(14)可以看出，这将导致射流对土壤的侵彻速度降低，且弹靶界面越接近土壤/混凝土界面，随着反射波的作用增强，侵彻速度越低。

透射波的质点速度虽然与射流侵彻速度方向相同，但由于透射波强度pCT远大于混凝土的侵彻阻抗，由式(16)和(17)可以看出，在透射波的作用下，同样导致射流对混凝土的侵彻速度降低，最终使得聚能射流对土壤/混凝土复合目标的侵彻深度大大下降。尽管土壤的密度和强度均小于混凝土，但由于界面效应的影响，在土壤厚度一定的情况下，反而使得聚能射流对土壤/混凝土复合目标的侵彻深度小于对单一混凝土靶的侵彻深度。

2　试验与分析

为了验证上述理论模型，分析界面效应对聚能射流侵彻土壤/混凝土复合目标的影响，采用如图3所示结构的聚能装药，分别进行了聚能射流侵彻350 mm土壤/700 mm混凝土复合靶和900 mm单一混凝土靶试验，其中聚能装药采用的炸药为Octol，药型罩材料为紫铜。试验装置见图4，混凝土靶为标准C40混凝土，土壤和混凝土靶板直径均为Φ1.5 m。

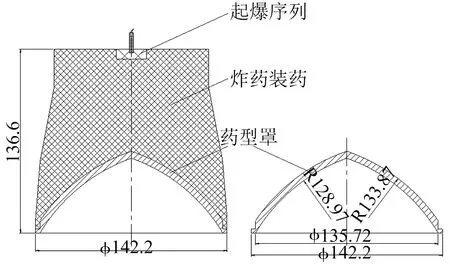
图3　试验用聚能装药结构Fig.3　The geometry of shaped charge used in experiments

图4　聚能装药侵彻单一混凝土靶、土壤/混凝土复合靶试验装置Fig.4　Test device of shaped charge penetration intoconcrete and soil/concrete target

聚能装药对两种靶板的侵彻效果见图5，该聚能装药完全穿透了900 mm单一混凝土靶，而对于350 mm土壤/700 mm混凝土复合靶，聚能射流穿透350 mm土壤后，对混凝土的侵彻深度仅为320 mm，即该聚能装药侵彻350 mm土壤/700 mm混凝土复合靶的总深度仅为670 mm。在土壤的密度和强度均小于混凝土的情况下，聚能射流对土壤/混凝土复合目标的侵彻深度却小于对单一混凝土目标的侵彻深度，表明应力波在土壤/混凝土界面的传播，对聚能射流侵彻土壤/混凝土复合目标产生了较大影响。

图5　聚能射流对单一混凝土靶、土壤/混凝土复合靶侵彻效果Fig.5　The concrete and soil/concrete target by shaped charge penetration

采用AUTODYN-2D仿真软件对射流形成过程进行了计算，具体计算方法见文献[15-16]，炸药和药型罩材料均为AUTODYN自带数据库材料，炸药为OCTOL，状态方程为JWL方程，药型罩材料为CU-OFHC，状态方程为Shock方程，强度模型为Steinberg Guinan模型，相关参数见AUTODYN数据库文件，得到的射流参数见图6。并采用上述理论模型对聚能射流侵彻土壤/混凝土复合靶和单一混凝土靶分别进行了计算，图7为不同侵彻深度时，聚能射流对土壤/混凝土复合靶和单一混凝土靶的侵彻速度曲线。对单一混凝土靶采用式(9)进行计算，而对土壤/混凝土复合靶则考虑界面效应的影响，根据侵彻过程的不同阶段，分别采用式(9)、式(13)和(14)以及式(16)和(17)进行计算。

图6　试验用聚能装药射流参数Fig.6　The parameters for the shaped charge jet

图7　不同侵彻深度时两种靶板侵彻速度曲线Fig.7　The penetration velocity of concrete and soil/concrete target

聚能射流侵彻土壤/混凝土复合目标时，由于混凝土的密度和强度均大于土壤，侵彻初期射流对土壤的侵彻速度大于对单一混凝土的侵彻速度，射流对土壤的侵彻深度为257 mm时，土壤/混凝土界面的反射波到达弹靶界面，致使聚能射流对土壤的侵彻速度急剧下降，当该现象引起的扰动在土壤/混凝土界面反射后，在射流侵彻深度为311 mm时到达弹靶界面，使得射流的侵彻速度又略有下降，而当聚能射流侵彻到混凝土时，由于透射波的作用，侵彻速度比单一混凝土靶中有所降低。经计算，该聚能装药对单一混凝土靶的侵彻深度为911 mm，而对350 mm土壤/700 mm混凝土复合靶的侵彻深度为677.5 mm，与试验结果一致。

3　结　论

(1)聚能射流侵彻土壤/混凝土复合目标时，侵彻过程中产生的塑性波到达土壤/混凝土界面时发生反射和透射，进而对侵彻过程产生影响；

(2)分别考虑反射波对射流侵彻土壤，以及透射波对射流侵彻混凝土过程的影响，建立了聚能射流侵彻土壤/混凝土复合目标的理论模型；

(3)理论分析表明，由于土壤/混凝土界面效应的影响，在反射波和透射波作用下，聚能射流对土壤和混凝土的侵彻速度急剧下降，在土壤厚度一定的情况下，反而使得聚能射流对土壤/混凝土复合目标的侵彻深度小于对单一混凝土靶的侵彻深度；

(4)采用相同结构聚能装药分别对单一混凝土靶和土壤/混凝土复合靶进行了侵彻试验，结果表明，射流对土壤/混凝土复合靶的侵彻深度比单一混凝土靶有所降低。根据理论计算得到的聚能射流对两种靶板侵彻深度与试验结果一致。

[1]HUERTA M,VIGIL M G.Design,analyses,and field test of a 0.7m conical shaped charge[J].International Journal of Impact Engineering,2006,32(8):1201-1213.

[2]LUK V K,FORRESTAL M J.Penetration into semi-infinite reinforced concrete targets with spherical and ogival nose projectiles[J].International Journal of Impact Engineering,1987,6(4):291-301.

[3]FORRESTAL M J,LUK V K.Penetration into soil target[J].International Journal of Impact Engineering,1992,12(3):427-444.

[4]FORRESTAL M J,FREW D J,HICKERSON J P,et al.Penetration of concrete targets with deceleration-time measurements[J].International Journal of Impact Engineering,2003,28(5):479-497.

[5]VOOREN A V,BORG J,SANDUSKY H,et al.Sand penetration:a near nose investigation of a sand penetration event[J].Procedia Engineering,2013,58:601-607.

[6]SHI C C,WANG M Y,LI J,et al.A model of depth calculation for projectile penetration into dry sand and comparison with experiments[J].International Journal of Impact Engineering,2014,73:112-122.

[7]CHURCH P,CORNISH R,CULLIS I,et al.General overview of capability in the simulation of shaped charges penetrating soil/concrete targets[C]//19th International Symposium on Ballistics,2001:1053-1060.

[8]蒋志刚,甄明,刘飞,等.钢管约束混凝土抗侵彻机理的数值模拟[J].振动与冲击,2015,34(11):1-6.

JIANG Zhigang,ZHEN Ming,LIU Fei,et al.Simulation of anti-penetration mechanism of steel tube confined concrete[J].Journal of Vibration and Shock,2015,34(11):1-6.

[9]张兆军,王晓鸣,李文彬.粗骨料种类对刚性弹贯穿混凝土靶剩余速度的影响[J].振动与冲击,2014,33(7):170-173.

ZHANG Zhaojun,WANG Xiaoming,LI Wenbin.Effect of coarse aggregate type on residual velocity of rigid-projectiles-perforation concrete targets[J].Journal of Vibration and Shock,2014,33(7):170-173.

[10]纪冲,龙源,高振儒,等.弹丸冲击贯穿有限厚混凝土材料靶板的背面成坑效应[J].振动与冲击,2013,32(4):85-89.

JI Chong,LONG Yuan,GAO Zhenru,et al.Rear face crater-forming of a limited-thickness concrete target due to projectile penetrating[J].Journal of Vibration and Shock,2013,32(4):85-89.

[11]蔺建勋,蒋浩征,蒋建伟,等.弹丸垂直侵彻土壤混凝土复合介质的理论分析模型[J].弹道学报,1999,11(1):1-10.

LIN Jianxun,JIANG Haozheng,JIANG Jianwei,et al.An analytical model for projectile normally into layered target of soil/concrete[J].Journal of Ballistics,1999,11(1):1-10.

[12]赵久奋,闫肃,李庆震,等.弹丸侵彻混凝土、土壤复合介质分析模型[J].弹道学报,2004,16(3):55-59.

ZHAO Jiufen,YAN Su,LI Qingzhen,et al.The theoretical analysis model on submunition penetration compound medium[J].Journal of Ballistics,2004,16(3):55-59.

[13]周玉兵.带覆土层混凝土结构的斜侵彻研究[D].南京:南京理工大学,2013.

[14]MEYERS M.材料的动力学行为[M].张庆明,刘彦,黄风雷,等译.北京:国防工业出版社,2006.

[15]XIAO Q Q,HUANG Z X,ZHU C S,et al.Calculation of depth and crater diameter for the supersonic penetration of shaped charge jet into concrete[J].Propellants,Explosives,Pyrotechnics,2013,38(2):224-231.

[16]XIAO Q Q,HUANG Z X,ZU X D,et al.Penetration research of jacketed jet into concrete[J].International Journal of Impact Engineering,2013,54:246-253.

Shaped charge jet penetrating into soil/concrete target

XIAO Qiangqiang1,2,LIU Rongzhong2,FENG Chengliang1,HUANG Zhengxiang2,WEI Xuchang1

(1.Chongqing Hongyu Precision Industrial CO.,LTD.Bishan 402760,China;2.College of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)

In order to study penetration capability of shaped charge jet penetrating into a soil/concrete target,the response characteristics of the soil/concrete target under shaped charge jet penetration were analyzed.Considering propagation and attenuation of plastic wave and its reflection and transmission on soil/concrete interface,a theoretic model of shaped charge jet penetrating into the soil/concrete target was built by analyzing influence of reflection wave and transmission wave on the jet penetrating into the soil and concrete target.The comparative tests of jet penetrating into a concrete target and a soil/concrete target,respectively were performed.It was shown that the jet penetration depth into the soil/concrete target is lower than that into the concrete target owing to influences of reflecting wave and transmission one; the action of reflection wave and transmission wave,the penetration velocity decreases to cause the reduction of the jet penetration depth into the soil/concrete target; the test results agree well with those of theoretical analysis.

shaped charge; soil/concrete target; plastic wave; penetration depth; comparison tests

2015-04-08修改稿收到日期：2015-08-29

肖强强 男，博士，讲师，1985年3月生

刘荣忠 男，博士，教授，博士生导师，1956年1月生

O385；TJ413

A DOI:10.13465/j.cnki.jvs.2016.17.017