随机激励下汽车非线性悬架系统的混沌研究
牛治东,吴光强,2
(1.同济大学 汽车学院,上海 201804;2.东京大学 生产技术研究所,东京 153-8505)
随机激励下汽车非线性悬架系统的混沌研究
牛治东1,吴光强1,2
(1.同济大学 汽车学院,上海201804;2.东京大学 生产技术研究所,东京153-8505)
研究了具有迟滞非线性特性的单自由度悬架模型在随机激励下的混沌运动。运用随机梅尔尼科夫(Melnikov)方法,推导并得到有界噪声激励下系统在均方意义下发生混沌运动的临界条件,讨论了悬架迟滞参数对系统混沌运动的影响,并运用庞加莱截面、功率谱和最大李雅普诺夫指数(LLE)进行了数值验证,研究表明,悬架系统存在混沌运动。分析了C级路面激励下,汽车单自由度悬架迟滞非线性系统的随机响应,并运用庞加莱截面、功率谱和最大李雅普诺夫指数进行了数值模拟,揭示了此类系统在随机路面激励下发生混沌运动的可能性。
随机路面;迟滞非线性;汽车悬架;混沌
近年来,随机激励下非线性系统的混沌运动成为研究热点,但是对于汽车悬架非线性系统的研究多集中在周期、拟周期激励下系统的混沌运动,而对随机激励下悬架非线性系统的混沌运动研究较少,因此有必要对随机激励下悬架非线性系统进行研究。
对随机激励下非线性系统的混沌运动分析,应用较多的是随机Melnikov方法。杨绍普等[1]研究了具有滞后非线性特性的汽车单自由度悬架模型在路面随机激励下发生混沌运动的可能性,运用随机Melnikov方法得到均方意义下系统出现混沌运动的临界激励幅值,并通过最大Lyapunov指数和Poincaré截面进行了数值验证,但该模型用位移和速度的三次方描述悬架的滞后非线性,且通过正弦激励叠加高斯白噪声来模拟随机激励。王振佩等[2]利用随机Melnikov方法分析了有界噪声激励下Josephson系统的运动,并利用均方准则得到系统产生混沌的临界值,研究表明,有界噪声对系统混沌的产生起到了加速作用,且有界噪声的强度越大,混沌吸引子的发散程度越大,并对理论推导进行了数值验证,但没有分析系统参数对混沌临界值的影响。刘利琴等[3]建立了船舶的横摇非线性随机微分方程,运用随机Melnikov均方准则确定混沌运动的系统参数域,并得到了系统随机响应的概率密度函数,发现噪声强度大于混沌临界值时,船舶出现随机混沌运动。冯俊等[4]对有界噪声与谐和联合激励下的Duffing-Rayleigh振子的动力学行为进行研究,运用Melnikov随机方法得到系统出现混沌的条件,通过Poincaré截面和最大Lyapunov指数进行了数值验证。CHEN等[5]研究了具有迟滞非线性特性的磁流变阻尼器车辆悬架系统的混沌行为,采用分段二次函数设计的非线性反馈控制器来控制系统的混沌,同时利用Melnikov方法得到了控制器的系数,数值仿真表明该方法控制混沌的有效性。DOSTAL等[6]分析了船舶作为一个弱扰动哈密顿系统,在随机波浪激励下的骑浪运动,并利用随机梅尔尼科夫方法得到系统发生骑浪运动的近似概率。PÉREZ-POLO等[7]利用第一李雅普诺夫指数和梅尔尼科夫理论研究了被控制机电设备的混沌运动。但总的来说,以汽车作为研究对象的文献和相关内容相对较少。
本文采用幂函数多项式描述汽车悬架系统的迟滞非线性特性,建立了单自由度悬架非线性模型,研究了系统在有界噪声和C级路面分别激励下系统的动力学响应。采用随机Melnikov方法,推导出有界噪声激励下系统发生混沌运动的临界条件,并研究了迟滞参数对混沌运动的影响。通过Poincaré截面、功率谱和最大Lyapunov指数来研究系统的混沌运动,发现系统存在混沌运动,且随着路面激励幅值的增大,系统发生混沌的可能性越大。另外,还研究了悬架系统在C级路面激励下的随机响应,并运用Poincaré截面、功率谱和最大Lyapunov指数对系统模型进行数值模拟,发现了混沌运动的存在。
1 悬架迟滞模型与随机激励描述
1.1悬架迟滞模型
目前,描述悬架迟滞非线性模型应用较多的主要是双线性模型、迹法模型、干摩擦模型、Bouc-Wen 模型和Bingham模型等[8],本文根据悬架的动刚度和阻尼特性,采用幂函数多项式来描述汽车悬架迟滞非线性特性[9]
(1)
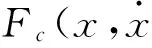
(2)
(3)
式中:k1、k3为非线性弹簧力系数;c为非线性阻尼力系数。n为阻尼因子,n=0时,系统中的阻尼为干摩擦阻尼;n=1时,为黏性阻尼;1>n>0时,阻尼中既有干摩擦阻尼,又有黏性阻尼;n>1时,阻尼表现为“高阶”阻尼。
1.2有界噪声
有界噪声是一个广义平稳的随机过程,具有非高斯概率分布。假设,ξ(t)为有界噪声[10]
ξ(t)=sin(ωt+ψ)
(4)
式中:ψ=σB(t)+χ。ω为平均激励频率;σ为频率随机扰动强度;B(t)为标准Wiener过程;χ是在[0,2π)上均匀分布的随机相位。
它的均值为零,谱密度为
(5)
有界噪声ξ(t)是一个广义平稳的随机过程,作为一个有界的随机过程,且是一个连续的样本函数,具有非高斯概率分布,它的均值为零。其谱密度在等级路面上的分布如图1所示,根据图中不同有界噪声强度下有界噪声的功率谱在等级路面中的分布,知有界噪声的功率谱在等级路面分级的合理范围内,可以认为有界噪声是合理的路面激励模型。

图1 不同σ下有界噪声的谱密度分布(Ω=1.5)Fig.1 Spectral density distributions of bounded noise under different σ(Ω=1.5)
1.3随机路面
随机路面的输入,一般用白噪声速度谱描述。作为车辆振动输入的路面不平度,主要采用路面功率谱密度来描述其统计特性。考虑速度对路面输入的影响,采用速度功率谱密度来描述路面不平度,则时间频率内的路面不平度[11]为
(6)
式中:Gq(n0)为参考空间频率下的路面功率谱密度值,称为路面不平度系数,单位为m2/m-1=m3;n0为参考空间频率,n0=0.1 m-1;v0为车速。
(7)
式中:w(t)为单位白噪声。
1.4汽车单自由度悬架迟滞非线性模型
汽车悬架迟滞模型如图2所示。图中:v0为汽车速度;z1为路面激励位移;z0为系统垂直位移;m为车体质量。
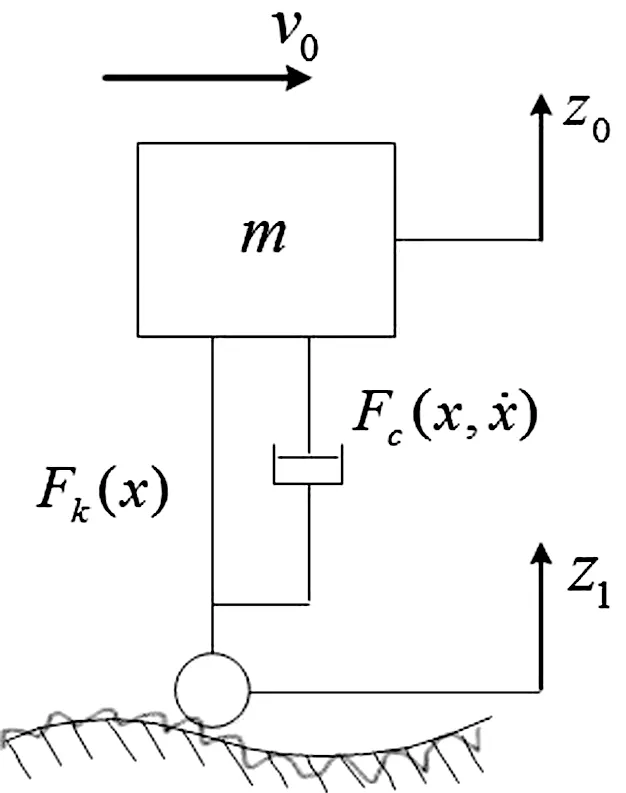
图2 随机激励下单自由度模型Fig.2 Single degree of freedom model under random excitation
则,系统的运动微分方程为
(8)
令z=z0-z1,则z0=z+z1。式(8)可转化为
(9)
2 有界噪声激励下迟滞系统的响应
2.1有界噪声激励下非线性系统的模型
假设汽车悬架迟滞非线性模型在有界噪声作用下,对式(9)进行变换得
(10)
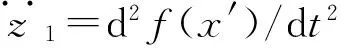
假设路面激励的随机部分为
d2f(x′)/d(x′)2=μξ(x′)
(11)
式中:μ为有界噪声的强度;ξ(x′)为单位有界噪声。
定义τ=ω0t,对式(10)进行无量纲化处理
(12)
将式(12)写成状态方程的形式:
(13)
2.2发生混沌的临界条件
当有界噪声激励可以忽略,且系统阻尼不存在时,其自由振动方程为
(14)

因,系统的哈密顿函数H满足
f1=∂H/∂x2,f2=-∂H/∂x1
则,哈密顿函数为
(15)
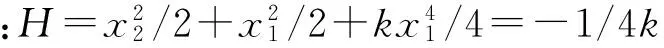
解得
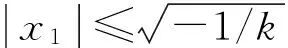
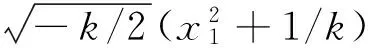
(16)

(17)
则,异宿轨道的方程为
(18)
式中:x1(τ)的正号表示异宿轨道的正轴部分,负号表示异宿轨道的负轴部分;x2(τ)的正号表示异宿轨道的上半部分,负号表示异宿轨道的下半部分。
则,系统的随机Melnikov过程为
(19)
令M(τ0)=Md-Mp(τ0),则:
本文研究在均方意义下,随机Melnikov过程出现简单零点的情况。Mp(τ0)为有界噪声引起的分量,其脉冲响应函数为
(20)
相应的频率响应函数为

(21)
从而有,
(22)
随机Melnikov过程在均方意义下出现零点的条件[14]为
(23)
对式(23)进行积分,得:
(24)
Melnikov函数具有简单零点,意味着稳定流形与不稳定流形用在庞加莱截面上横截相交,系统出现Smale变化意义下的混沌。对于悬架这个随机动力系统,在随机激励下,得到了均方意义下系统随机Melnikov过程出现零点的条件。运用数值方法对式(24)进行数值仿真,得到有界噪声激励幅值发生混沌的临界条件,如图3所示。参数:m=240 kg,k1=16 000 N/m,ω=5~35 rad/s,n=2,σ=0.5,k3=-10 000 N/m3,c=-50 N·s2/m2,v0=30 m/s。
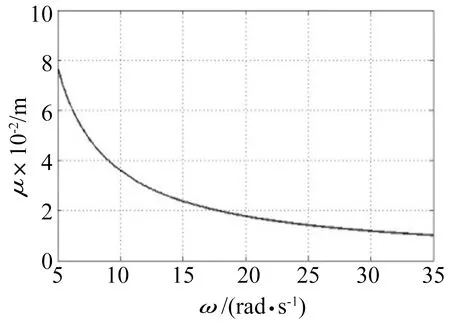
图3 发生混沌运动的临界幅值Fig.3 Critical condition of chaotic motion
当有界噪声的激励幅值落在曲线上面时,系统可能发生混沌运动;当有界噪声的激励幅值落在曲线下面时,系统不会出现混沌运动。
2.3迟滞参数对混沌临界值的影响
改变迟滞参数k1,k3,c的值,计算有界噪声激励下系统发生混沌域的影响,如图4所示。
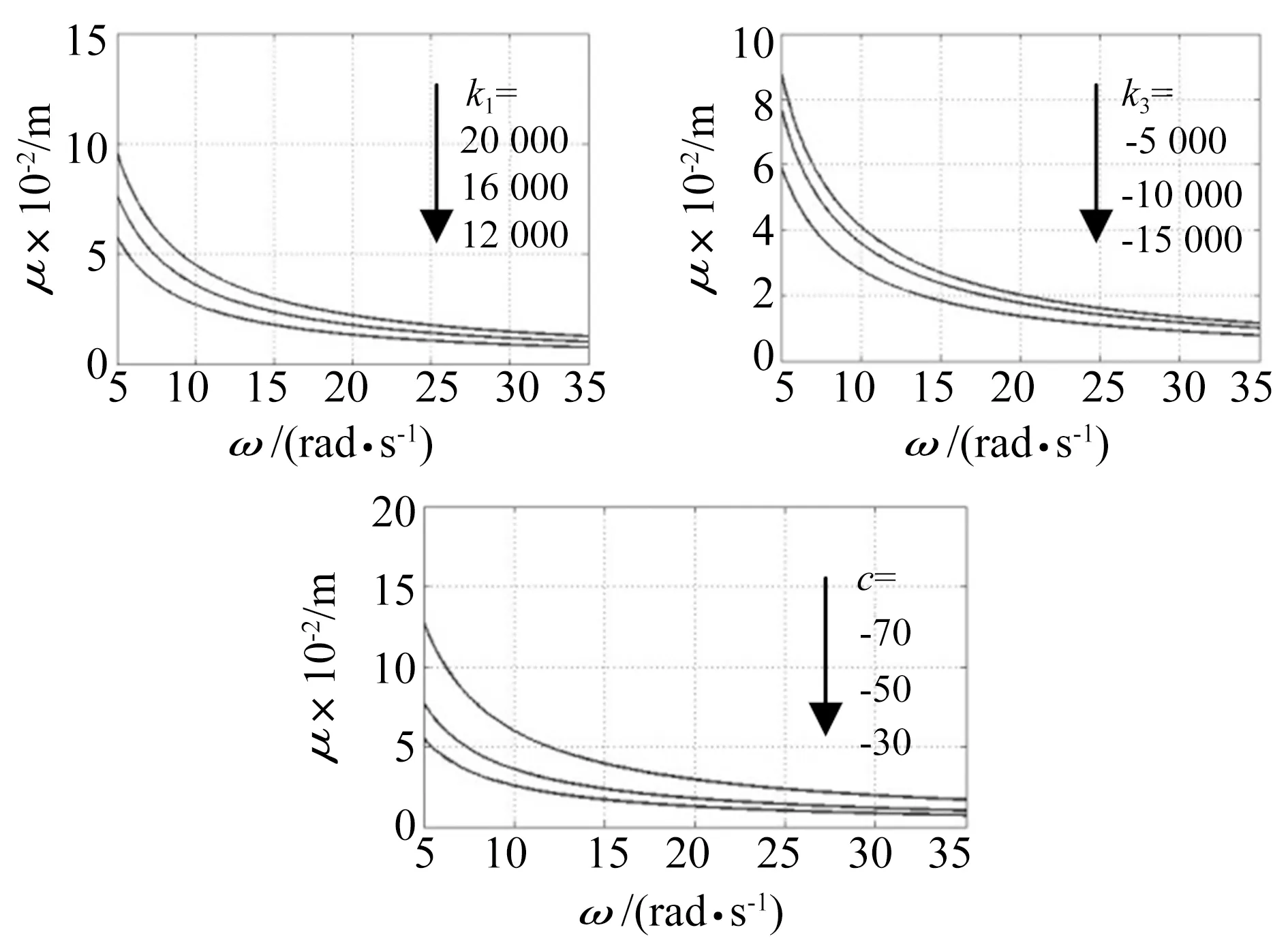
图4 迟滞参数对混沌域的影响Fig.4 Influence on chaos of parameters
从图4中各曲线的变化,可以看出:k1越大,混沌区域越大,发生混沌的可能性越小;k3越大,混沌区域越大,发生混沌运动的可能性越小;c越大,混沌区域越小,发生混沌的可能性越大。从图中还可推知,当系统所受的路面激励幅值较小时,系统不发生混沌运动,当路面激励幅值较大时,系统可能会发生混沌运动。
2.4有界噪声激励下迟滞系统的随机响应
选择参数ω=15 rad/s,改变激励幅值μ,令有界噪声激励幅值0.001 m、0.02 m、0.12 m,用数值方法对系统发生混沌运动的临界条件进行验证。分别计算不同激励幅值作用下系统的Poincaré截面、功率谱和最大Lyapunov指数,结果如图5,6,7所示。
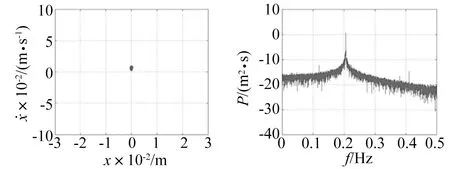
图5 μ=0.001 m,LEE=0Fig.5 μ=0.001 m,LEE=0
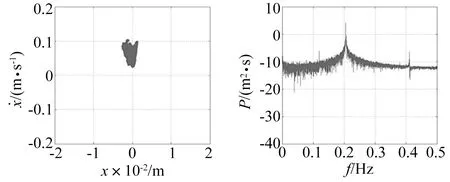
图6 μ=0.02 m,LEE=0.048 7Fig.6 μ=0.02 m,LEE=0.048 7
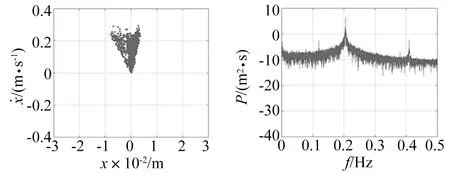
图7 μ=0.12 m,LEE=0.136 1Fig.7 μ=0.12 m,LEE=0.136 1
由数值结果可知,当激励幅值为0.001 m时,如图5所示,系统的Poincaré截面为一密集点集,系统的最大Lyapunov指数为零,说明此时系统为周期运动。当有界噪声的激励幅值为0.02 m时,如图6,系统的Poincaré截面为具有一定形状的密集点集,功率谱连续,且最大Lyapunov指数大于零,说明,系统处于混沌运动状态。同理,在图7中,当激励幅值为0.12 m时,系统也处于混沌运动状态。
比较图6和图7知,当激励幅值变大时,系统的Poincaré截面也随之变大。经过大量的计算,发现随着激励频率的变大,系统的混沌域有变大的趋势。当激励幅值较小时,系统不发生混沌运动,当激励幅值较大时,系统才有可能出现混沌运动。数值分析结果验证了2.4节关于有界噪声激励幅值发生混沌的临界条件的判断。
3 随机路面激励下系统的响应
对随机路面激励下系统的响应进行分析,假设系统处于C级路面激励下,固定车速v0=30 m/s,对式(8)在C级路面激励下进行数值模拟,计算系统的Poincaré截面、功率谱和最大Lyapunov指数,结果如图8所示。
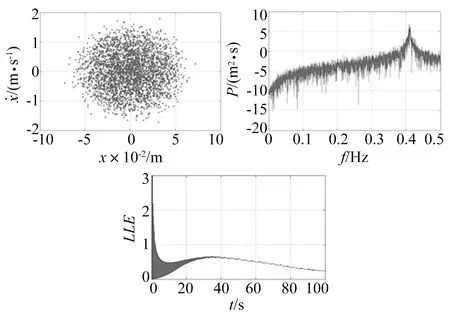
图8 C级路面激励下系统随机响应Fig.8 Stochastic response of system under the C-class road excitation
从数值仿真结果中发现,系统的Poincaré截面为一系列的密集点,功率谱连续,且最大Lyapunov指数大于零,说明系统此时处于混沌状态。
4 结 论
本文研究在有界噪声和C级路面激励分别激励下汽车悬架迟滞系统的动力学响应。分析了有界噪声激励下系统产生混沌运动的临界条件,并对其进行了数值验证。并利用C级路面激励验证了系统混沌运动的存在。
(1)采用幂函数多项式描述悬架的迟滞非线性特性,在此基础上建立了单自由度悬架迟滞非线性的运动微分方程。
(2)采用随机Melnikov方法,推导出有界噪声激励下系统发生混沌的临界条件,研究悬架各迟滞参数对混沌的影响。
(3)运用数值方法Poincaré截面、功率谱和最大Lyapunov指数来研究系统的混沌运动。研究发现系统存在混沌运动,且随着路面激励幅值的增大,系统发生混沌的可能性越大。
(4)研究了系统在C级路面激励下的随机响应,并运用Poincare截面、功率谱和最大Lyapunov指数谱,对系统模型进行数值模拟,发现混沌运动的存在。
[1]杨绍普,李韶华,郭文武.随机激励滞后非线性汽车悬架系统的混沌运动[J].振动.测试与诊断,2005,25(1):22-25.
YANG Shaopu,LI Shaohua,GUO Wenwu.Chaos in vehicle suspension system with hysteretic nonlinearity [J].Journal of Vibration,Measurement & Diagnosis,2005,25(1):22-25.
[2]王振佩,徐伟.有界噪声激励下Josephson系统的混沌运动[J].应用力学学报,2012,29(1):43-47.
WANG Zhenpei,XU Wei.Chaotic motion of a josephson system excited by bounded noise [J].Chinese Journal of Applied Mechanics,2012,29(1):43-47.
[3]刘利琴,唐友刚,吴志强.横浪中船舶的随机混沌运动[J].工程力学,2008,25(6):204-208.
LIU Liqin,TANG Yougang,WU Zhiqiang.Stochastic chaotic motion of ships in beam seas [J].Engineering Mechanics,2008,25(6):204-208.
[4]冯俊,徐伟,顾仁财,等.有界噪声与谐和激励联合作用下 Duffing-Rayleigh 振子的 Melnikov 混沌[J].物理学报,2011,60(9):090507(1-8).
FENG Jun,XU Wei,GU Rencai,et al.Melnikov chaos in duffing-rayleigh oscillator subjected to combined bounded noise and harmonic excitations [J].Acra Phys.Sin,2011,60(9):090507(1-8).
[5]CHEN Lijie.Controlling chaos in automobile suspension system with nonlinear feedback controller [C]//2nd International Conference on Precision Mechanical Instruments and Measurement Technology,ICPMIMT 2014,1103-1108.
[6]DOSTAL L,KREUZER E.Surf-riding threshold of ships in random seas [J].Proceedings in Applied Mathematics and Mechanics,2013,13(1):383-384.
[7]PÉREZ-POLO M F,PÉREZ-MOLINA M.Steady-state self-oscillations and chaotic behavior of a controlled electromechanical device by using the first Lyapunov value and the melnikov theory [J].Journal of Sound and Vibration,2014,333(4):1163-1181.
[8]李韶华,杨绍普.滞后非线性模型的研究进展[J].动力学与控制学报,2006,4(1):8-15.
LI Shaohua,YANG Shaopu.Research status of hysteretic nonlinearity models [J].Journal of Dynamic and Control,2006,4(1):8-15.
[9]龚宪生,唐一科.一类迟滞非线性振动系统建模新方法[J].机械工程学报,1999,35(4):11-14.
GONG Xiansheng,TANG Yike.New method for modeling of a nonlinear vibration system with hysteresis characteristics [J].Chinese Journal of Mechanical Engineering,1999,35(4):11-14.[10]LIU W Y,ZHU W Q,HUANG Z L.Effect of bounded noise on chaotic motion of duffing oscillator under parametric excitation [J].Chaos,Solitons & Fractals,2001,12(3):527-537.
[11]余志生.汽车理论[M].北京:机械工业出版社,2009.
[12]盛云,吴光强.汽车非线性悬架的混沌研究[J].汽车工程,2008(1):57-60.
SHENG Yun,WU Guangqiang.A chaos research on vehicle nonlinear suspension system [J].Automotive Engineering,2008,30(1):57-60.
[13]李韶华,杨绍普.拟周期激励下滞后非线性汽车悬架的混沌[J].振动与冲击,2003,22(3):61-64.
LI Shaohua,YANG Shaopu.Chaos in suspension system with hysteretic nonlinearity under quasi-period excitation [J].Journal of Vibration and Shock,2003,22(3):61-64.
[14]朱位秋.非线性随机动力学与控制:Hamilton 理论体系框架[M].北京:科学出版社,2003.
Chaos of a vehicle nonlinear suspension system under stochastic excitation
NIU Zhidong1,WU Guangqiang1,2
(1.College of Automotive Studies,Tongji University,Shanghai 201804,China;2.Institute of Industrial Science,the University of Tokyo,Tokyo 153-8505,Japan)
Chaotic motions of a single DOF vehicle suspension system with nonlinear hysteretic characteristics under random excitation were studied.By using stochastic Melnikov method,the critical condition to cause chaotic motion of the system under bounded noise excitation was derived in the mean square sense.The influences of suspension hysteretic parameters on the system’s chaotic motion were discussed,and the numerical validation was performed by using Poincaré section,power spectrum and the largest Lyapunov exponent (LLE).The results showed that there exist chaotic motions in the suspension system.The random responses of the single DOF vehicle suspension system with nonlinear hysteretic characteristics under the C-class road excitation were simulated and analyzed by using Poincaré section,power spectrum and the largest Lyapunov exponent.The numerical simulation revealed the possibility of the occurrence of chaotic motions in this kind system under stochastic road excitation.
stochastic road; hysteretic nonlinearity; vehicle suspension; chaotic
教育部高等学校博士学科点专项科研基金(20120072110013)
2015-05-18修改稿收到日期:2015-08-14
牛治东 男,博士生,1987年4月生
吴光强 男,教授,博士生导师,1965年11月生
U461;O324
A DOI:10.13465/j.cnki.jvs.2016.17.007

