DMC算法在电加热炉时滞系统中的仿真研究

何美霞，周箩鱼，杨友平

(长江大学电子信息学院，湖北 荆州 434023)



DMC算法在电加热炉时滞系统中的仿真研究

何美霞，周箩鱼，杨友平

(长江大学电子信息学院，湖北 荆州 434023)

对电加热炉时滞系统的优化控制研究中，系统炉温的控制是至关重要的。而电加热炉的温度具有时变性、滞后性和大惯性等特性，常规的PID控制难以保证效果。为此，引入一种先进的控制——动态矩阵控制(DMC)。介绍了DMC的算法原理，给出算法实施的具体步骤；针对已辨识出的一阶时滞电加热炉模型，设计DMC控制器。仿真研究表明，相对于传统的PID控制，动态矩阵控制能兼顾调节时间短、超调量小的优点，在系统时滞变化的情况下，DMC依旧能保持良好的控制效果。因此，对于一阶时滞系统的优化控制，DMC是一种值得推广的控制方法。

动态矩阵控制；控制器；电加热炉；时滞系统

电加热炉具有清洁环保、热效能高、使用维护方便的特点，广泛应用于化验品样品溶样、金属冶炼、零件热处理、化工精馆、生物发酵等领域。但电加热炉是集时滞、时变和非线性于一体的复杂控制对象。对于控制精度要求不高的场合，采用PID控制尚能满足系统的性能要求，但是当系统参数变化时，传统的PID控制已经不能满足要求。因此，需要寻找一种能更适合电加热炉温度特性的有效控制方式[1]。

动态矩阵控制(Dynamic Matrix Control，DMC)是一种基于非参数模型的控制算法，包含了预测模型、滚动优化、反馈校正3个要素[2]。DMC采用多步预测模型输出的方法以扩大反映被控对象未来变化趋势的信息量，从而可以克服各种不确定性因素对被控系统的影响。DMC算法与传统PID控制不同，它以输入增量直接作为控制量，在控制中包含了数字积分环节，因而在系统模型失配的情况下，也能实现无静差控制[3]。下面，笔者首先介绍了DMC算法的主要原理，分析了其实施的具体步骤；进而针对已辨识出的电加热炉模型，给出了具体的DMC控制器的程序设计方法；最后将该控制器应用在电加热炉模型中进行仿真研究。

1　DMC算法原理及实施步骤

DMC算法通过求取二次型性能指标的最优，来确定未来的最优输入；计算出一组最优输入序列后仅将序列中的第一个输入应用于被控对象；到下一采样时刻，先检测被控对象的实际输出，并利用这一实时输出信息对预测值进行修正，再进行新的滚动优化[4]。用到的主要符号及含义如表1所示。

1.1算法原理

假设系统处于稳态，在单位阶跃输入Δu作用下，时不变单输入单输出(Single Input Single Output，SISO)系统的输出恰好在变化N步后达到稳态，这样对象的动态信息就可以近似地用有限集{s1,s2,…,sN}加以描述。这个集合的参数构成了DMC的模型向量s=[s1,s2,…,sN]T。

表1　主要符号及含义

根据叠加原理，利用系统阶跃响应模型向量，可推出预测模型为：

(k|k)

(1)

式中：

(k|k)=[y(k+1|k),y(k+2|k),…,y(k+P|k)]T

(k|k)=[y0(k+1|k),y0(k+2|k),…,y0(k+P|k)]T

未来k+j时刻的参考轨迹为：

(2)

式中，ys(k+j)=ays(k+j-1)+(1-a)yss,j∈{1,2,…,P},a∈(0,1)。一般取ys(0)=y(0)。

在DMC算法中，为使系统的输出预测值尽可能接近期望目标，可通过极小化如下性能指标以求解最优控制输入增量：

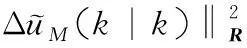
(3)

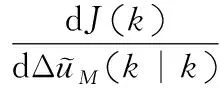
=0，求得：

(4)

式(4)给出了Δu(k),Δu(k+1|k),…,Δu(k+M-1|k)的最优值。但DMC只取即时控制增量Δu(k)构成实际控制量u(k)=u(k-1)+Δu(k)作用于被控对象。到下一时刻，它又求解类似的优化问题，得到Δu(k+1)。这就是所谓的“滚动优化”策略。

因此在每个时刻k，DMC算法的最优控制增量为：

(5)

式中，dT=[1,0,…,0](ATWA+R)-1ATW。

P0(k|k)时，由于实际系统中存在非线性、环境干扰、模型失配等未知因素的影响，基于不变模型的预测输出不可能与系统的实际输出完全吻合，因此需要将系统的实际输出值与预测值比较得到的预测误差加以校正。具体步骤为：

1)在每个时刻k>0，计算：

ε(k)=y(k)-y(k|k-1)

y(k|k-1)=y0(k|k-1)+sΔu(k-1)

2)计算：

(6)

其中：

(k-1+N|k-1)]T

A1=[s2,s3,…,sN,sN]T

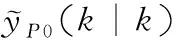
1.2实施步骤

在运用DMC算法时，可按照以下步骤实施[4]：

步2在k=0时：

1)测量系统的实际输出y(0)；

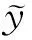
4)计算：

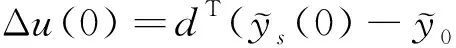
5)实施Δu(0)。

步3在k>0时：

1)测量输出y(k)；

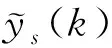
3)计算：

ε(k)=y(k)-y(k|k-1)

其中：

y(k|k-1)=y0(k|k-1)+s1Δu(k-1)

4)计算：

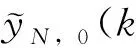
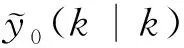
5)计算：

6)实施Δu(k)。

2　控制器程序设计

文献[5]中，对电加热炉在常温下加30%量程控制量，经数据采集，辨识出该加热炉的模型为：

(7)

式中，k=1.347；T=60.9；τ=2.333。

笔者采用式(7)作为电加热炉时滞系统的近似模型。对电加热炉模型的详细描述请参看文献[6]。

基于DMC算法原理，设计电加热炉时滞系统的控制器需要解决以下2个方面的问题[7]：①初始参数的离线计算。算法步骤中的部分参数一旦设定以后，整个过程不会发生变化。此时，可将这部分参数用Matlab编程为初始化程序。此程序一旦运行则参数设定完成。②实时参数的在线计算。DMC算法每次运行只取最优输入序列中的第一项使用，被控对象的实时输出每一时刻也不尽相同。因此用于计算最优输入序列的这部分参数需要在线计算。

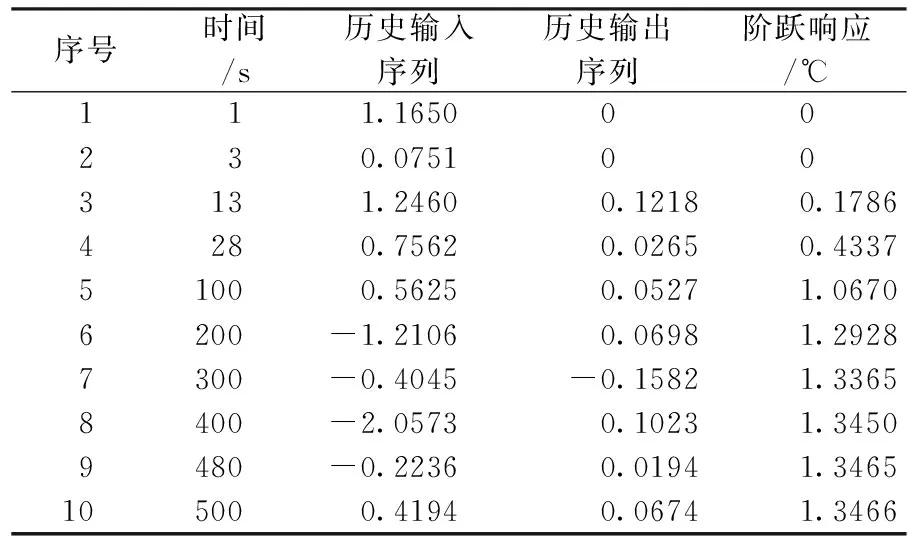
表2　历史信息及阶跃响应部分数据

笔者采用Matlab编程和Simulink建模方法[8]解决。 DMC控制器的程序设计具体步骤实现如下：

步1获取对象的历史信息和阶跃响应。

取采样时间Ts=1s，仿真时长为500s，获取的历史输入、输出序列信息与阶跃响应部分数据如表2所示。

步2选择N,P,M参数获得A,A1。

N=500; P=40;M=30;A=zeros(P,M); A(:,1)=s(1:P);

for i=2:M

aa=[zeros(1,i-1) s(1:P-i+1)'];

A(:,i)=aa';

end

A1=[s(2:end);s(end)];

步3选择W,R参数获得dT,Δu(0)。

W=1*eye(P);R=1*eye(M);dT=[1 zeros(1,M-1)]*inv((A'*W*A+R))*A'*W;

y=yp(101);YN0(1:N,1)=y;a=.1;yss=600;ys(1,1)=y;

for i=2:P

ys(i,1)=a*ys(i-1,1)+(1-a)*yss;

end

du=dT*(ys-YN0(1:P));

ys(1,1)=y;

for i=2:P

ys(i,1)=a*ys(i-1,1)+(1-a)*yss;

end

YN00=[YN0(2:end);YN0(end)];y_0=YN0(1)+s(1)*du;

E=y-y_0;F=1*ones(N,1);YN0=YN00+A1*du+F*E;

步6计算k>0 时的Δu(k),u(k)。

du=dT*(ys-YN0(1:P));u=up(1)+du;up=[u;up(1:end-1)];

步1～步3完成初始化参数的计算，步4～步6实现DMC控制器的实时计算。

3　仿真研究

3.1最优参数

为选取DMC及PID这2种控制的最优参数，设定控制目标yss=1℃进行仿真测试，仿真效果如图1和图2所示。

图1　DMC参数选择仿真测试

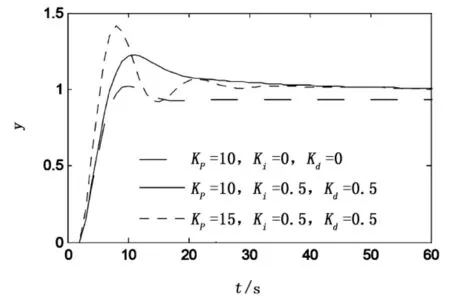
图2　PID参数选择仿真测试

从图1可以看出，仿真时间为250s左右系统才能达到设定目标；参数的变化不影响系统最终的稳态值，但影响系统的调节时间和超调量；当参数N=500，P=40，M=30，W=R=diag(1,1,…,1)时的仿真效果最理想，此时不仅快速性好、调节时间短、无超调量，且无稳态误差。从图2可以看出系统在50s左右稳定；参数的变化会影响系统的快速性、调节时间和稳定值；当KP=10、Ki=KP=0时系统存在稳态误差，而当KP=15、Ki=KP=0.5时系统的超调量变大，因此要兼顾快速性好，超调量小、零稳态误差等特性，最优参数为：KP=10、Ki=0.5、KP=0.5。

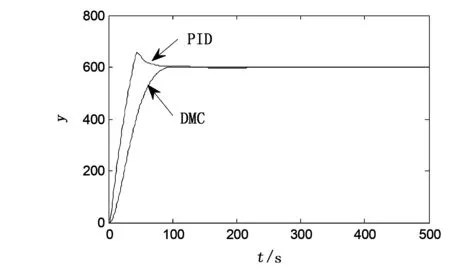
图3　DMC与PID控制对比

3.2理想情况

假设系统处于理想情况，系统的控制目标为yss=600℃，采用式(5)中的模型进行仿真，DMC与PID控制效果如图3所示，其具体的性能指标数值如表3所示。从图3和表3看出，采用PID控制时，系统快速性虽较好(38s输出第一次就达到设定值)，但有9.5%的超调；DMC控制的快速性虽不及PID控制(慢了54s)，但它超调仅为0.83%；此外两者的调节时间均为140s。

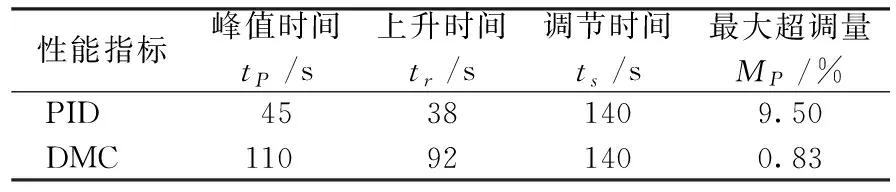
表3　PID与DMC性能指标对比

由于实际系统的时滞τ容易发生变化，因此需对这种情况加以仿真进一步研究2种控制的目标跟踪能力、快速性及鲁棒性能。

3.3时滞变化

式(7)中的数值τ发生变化时，系统模型处于失配状态。逐步增大式(7)模型中时滞τ的数值，仿真效果如图4～图7所示。

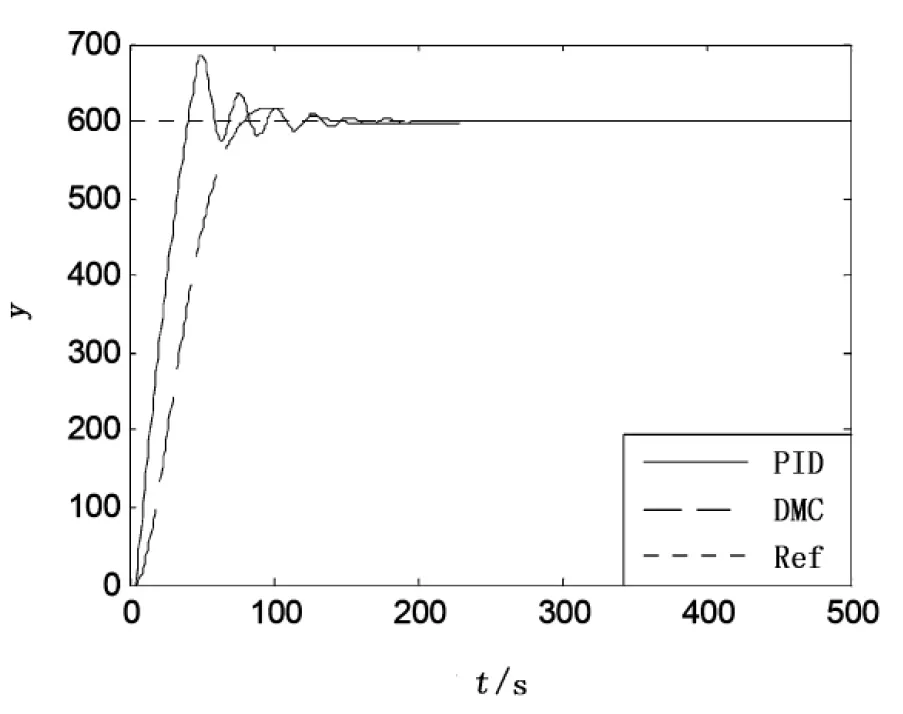
图4　τ=5仿真效果

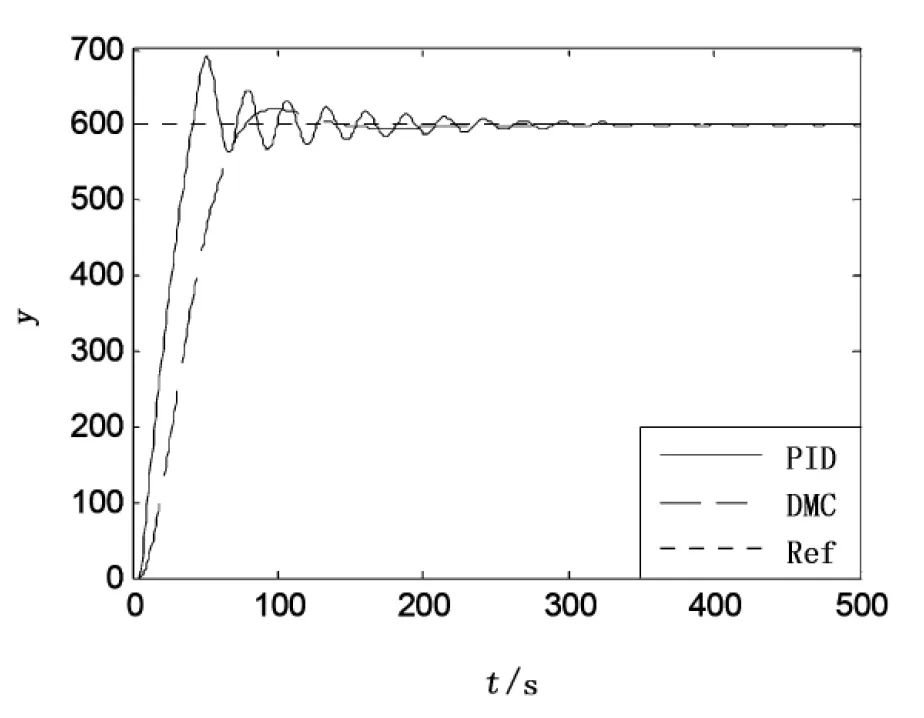
图5　τ=5.5仿真效果

从图4～图7可以看出，当τ=5时，PID控制出现较大超调，约250s才逐渐稳定；当τ=5.5时，收敛时间变长，350s才稳定；τ=6时，不能收敛，出现小幅度震荡；当τ=10时，震荡进一步加大；在整个时滞τ变化过程中，DMC控制始终能保持较好的快速性，较小的超调量及零稳态误差。

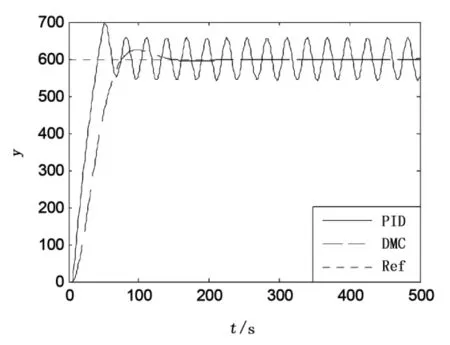
图6　τ=6仿真效果

图7　τ=10仿真效果

4　结语

电加热炉是集时滞、时变和非线性于一体的复杂控制对象，采用传统PID控制有时达不到预期的效果。笔者引入动态矩阵控制，设计DMC控制器对其进行仿真研究。仿真结果表明，PID控制具有较快的峰值时间和上升时间，但却有较大的超调量，且当系统的时滞发生变化时，其控制效果逐渐变差，最后出现震荡；DMC能兼顾调节时间短和超调量小的优点，且能有效克服电加热炉时滞变化对系统的影响问题，保持良好的控制性能。因此相对于传统的PID控制，DMC更加适合解决一阶时滞系统的优化控制问题，是一种值得推广的控制方法。

[1]余昌源.电加热锅炉温度控制系统旳设计及实现[D].内蒙古:内蒙古大学, 2014.

[2]丁宝苍.预测控制的理论与方法[M].北京:机械工业出版社,2008.

[3]丁宝苍.先进控制理论[M].北京:电子工业出版社,2010.

[4]何美霞.预测控制软件包的设计与仿真研究[D].重庆:重庆大学, 2012.

[5]潘红华, 苏宏业, 褚健.预测函数控制及其在工业电加热炉中的应用[J].机电工程,1999(5):130～132.

[6]赵治月.基于PID算法的电加热炉温度控制系统设计[J].沧州师范学院学报,2016,32(1):59～63.

[7]吕亚峰, 郭利进, 成立存.基于动态矩阵控制的聚合釜温度控制与仿真[J].计算机仿真,2014,31(7):198～201.

[8]何美霞, 杨友平.基于Simulink的连续搅拌反应釜的建模与仿真[J] .长江大学学报(自科版), 2015, 12 (28): 21～25.

[编辑]洪云飞

2016-04-27

湖北省教育厅科研计划资助项目(Q20151302)；长江大学教学研究项目(JY2014031)。

何美霞(1986-)，女，硕士，助教，现主要从事预测控制、过程控制的仿真方面的教学与研究工作；E-mail：1131366980@qq.com。

TP273

A

1673-1409(2016)22-0023-06

[引著格式]何美霞，周箩鱼，杨友平.DMC算法在电加热炉时滞系统中的仿真研究[J].长江大学学报(自科版)，2016,13(22)：23～28.