大跨度连续梁拱组合桥梁轨互制特征

王伟民

(中铁第四勘察设计院集团有限公司，武汉　430063)



大跨度连续梁拱组合桥梁轨互制特征

王伟民

(中铁第四勘察设计院集团有限公司，武汉430063)

为研究大跨度连续梁拱组合桥梁轨相互作用特征，以梅汕线上某(34+160+34)m刚架系杆拱钢箱连续梁组合桥为背景，采用理想弹塑性模型模拟线路纵向阻力，建立 “轨-拱-梁-墩”一体化空间模型，对钢轨纵向力的分布规律进行分析，对是否考虑轨道作用下的主梁应力、梁端转角、墩底纵向反力进行比较。结果表明：连续梁拱组合桥远离固定支座的梁端处钢轨纵向力较大，其中最大伸缩应力达到114.0 MPa，在不设钢轨伸缩调节器时钢轨强度仍满足要求；轨道结构对温度荷载和制动力作用下的主梁应力影响较大；轨道结构对梁端转角及墩底纵向反力的分配亦有较大影响。

连续梁拱组合桥；钢轨纵向力；轨道作用；主梁应力；梁端转角；墩底纵向反力

关于铁路桥梁与钢轨的互制特征，国内外学者做了较为广泛的研究[1-4]。近年来，随着铁路建设的发展，铁路线路上出现了大量的特殊桥梁结构，如拱桥、斜拉桥、钢桁梁桥等。对于大跨度连续梁拱组合桥，梁轨相互作用的研究较少，且大多只分析了钢轨的纵向受力，而对桥梁受力变化的研究较少。

本文在前人研究的基础上，建立了考虑轨道空间位置的轨-拱-梁-墩一体化有限元模型，以梅州至潮汕客运专线上某(34+160+34) m刚架系杆拱钢箱连续梁组合桥为工程背景，研究该连续梁拱组合桥上钢轨纵向力的分布规律，以及其对桥梁受力的影响。

1　梁轨计算模型和参数

本工程位于梅汕铁路线上，主桥为(34+160+34) m刚架拱连续梁组合体系，拱肋与主墩固结，主梁为半漂浮体系，正常情况下右侧主墩纵向固定，其余均为纵向活动。主梁采用单箱三室扁平钢箱梁；拱肋采用钢管混凝土结构，矢跨比为1/4；两榀拱肋之间设7道横撑；全桥共设17组吊杆，吊杆顺桥向间距为8 m，横向间距为13.9 m；每侧设4束可换索式钢绞线系杆。桥上铺设双线有砟轨道，线间距为4.6 m，轨道采用60 kg/m钢轨。

梁轨相互作用模型的关键，在于轨道与桥梁接触方式的模拟[5-9]。本文假设轨道横向和竖向与桥梁不发生相对位移，采用梁单元模拟主梁、拱肋、桥墩、钢轨，采用桁架单元模拟吊杆、系杆，采用非线性弹簧模拟线路纵向阻力。主桥左侧建3跨32 m简支梁，主桥右侧建4跨24 m简支梁来减少边界条件的影响，建立的有限元模型如图1所示。

图1　梁轨相互作用有限元模型(单位：cm)

对于有砟轨道，线路纵向阻力取道床阻力，线路纵向阻力模型采用《铁路无缝线路设计规范》中有砟轨道理想弹塑性模型，即认为当梁轨纵向相对位移超过2 mm后，线路纵向阻力保持不变，线路纵向阻力[10-12]

式中，r为线路纵向阻力，kN/m/线；u为梁轨纵向相对位移，mm。

计算钢轨伸缩力时，考虑钢结构整体升温30 ℃，混凝土结构整体升温22 ℃；计算钢轨挠曲力时，采用ZK中64 kN/m均布荷载分单双线加载，加载长度取400 m，从左侧32 m简支梁梁端开始加载；计算钢轨制动力时，制动力率取0.164[13]，加载位置同挠曲力，分左侧入桥和右侧入桥两种情况进行计算。

2　连续梁拱组合桥上无缝线路纵向力特点

2.1钢轨伸缩力

钢结构整体升温30 ℃，混凝土结构整体升温22 ℃时，钢轨伸缩力分布特征如图2所示，梁轨纵向位移如图3所示。

图2　钢轨伸缩应力

由计算可知，钢轨最大伸缩拉应力为71.4 MPa，出现在主跨跨中向右10 m处；钢轨最大伸缩压应力为114.0 MPa，出现在连续梁拱组合桥左侧梁端。该大跨度连续梁拱组合桥钢轨伸缩力分布规律与一般连续梁上钢轨伸缩力分布规律一致。

图3　梁轨纵向位移

由图3可知，主梁的纵向位移在4号墩活动支座端达到最大值，其值为64.7 mm，而钢轨最大纵向位移为37.3 mm，发生在钢轨坐标为30 m处。在连续梁拱组合桥范围内，有一段长度主梁纵向位移和钢轨纵向位移基本相等，从图2可看出该范围内钢轨伸缩应力也基本保持不变。

2.2钢轨挠曲力

挠曲力分为单线加载和双线加载，从1号墩处开始加载，加载长度为400 m。加载时取ZK荷载中的均布荷载64 kN/m。钢轨挠曲力分布特征如图4所示。

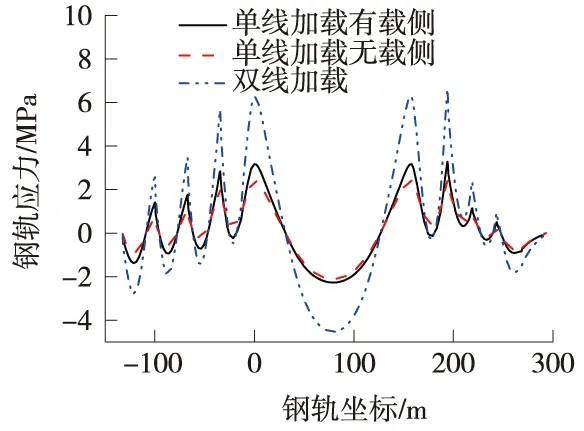
图4　钢轨挠曲应力

单线加载时，有载侧钢轨挠曲拉应力最大值为3.3 MPa，发生在连续梁拱组合桥右侧梁端，压应力最大值出现在主跨跨中，其值为2.3 MPa；无载侧钢轨挠曲应力较有载侧钢轨略小，但其变化趋势基本一致。双线加载时，钢轨挠曲拉应力和压应力的最值分别为6.6 MPa和4.5 MPa，其分布规律与单线加载时一致。

2.3钢轨制动力

制动力分单线制动和双线制动，只考虑相同方向制动，分左侧入桥和右侧入桥两种情况，制动力加载范围同挠曲力，列车制动力大小取10.5 kN/m，钢轨制动力分布特征如图5所示。

图5　钢轨制动应力

钢轨制动力最大值发生在连续梁拱组合桥左侧梁端处。单线制动时，有载侧钢轨最大制动应力为9.2 MPa，无载侧钢轨最大制动应力为5.5 MPa；反向加载时，钢轨制动应力大小保持不变，符号相反；双线制动时，钢轨最大制动应力为16.3 MPa。

2.4钢轨强度

根据我国《铁路无缝线路设计规范》(TB10015—2012)[14]，对钢轨强度进行检算，其检算公式为

式中σ底d——轨底边缘动弯应力，MPa；

σt——钢轨最大温度应力，MPa；

σf——钢轨最大附加应力，取桥上无缝线路伸缩附加应力和挠曲附加应力的较大值，MPa；

σz——钢轨制动(牵引)应力，MPa；

[σ]——钢轨容许应力，MPa；

σs——钢轨钢屈服强度，对于U75V钢轨，其屈服强度为472 MPa；

K——安全系数，取1.3。

由《铁路无缝线路设计规范》(TB10015—2012)及文献[15]可知σ底d的值可取为114.1 MPa；σt=EαΔT，考虑钢轨升降温40 ℃，可得σt=97.2 MPa；σf取钢轨最大伸缩应力，为114.0 MPa；σz取钢轨最大制动应力，σz=16.3 MPa；σ底d+σt+σf+σz=341.6 MPa，钢轨容许应力[σ]=363.1 MPa，因此不设钢轨伸缩调节器，能满足钢轨强度要求。

3　考虑轨道结构与否对桥梁受力的影响

3.1主梁应力

钢轨与桥梁之间存在约束关系，因此钢轨纵向力会反作用于桥梁。对于该刚架系杆拱钢梁连续梁组合桥，轨道作用对拱肋及吊杆受力影响很小，因此仅讨论其对主梁受力的影响。

钢结构升温30 ℃，混凝土升温22 ℃时，主梁应力如图6所示。从图中可以看出轨道的参与对主梁在温度荷载作用下的受力情况有较大影响。考虑轨道结构影响时，主梁最大应力为13.9 MPa，为压应力，发生在主跨跨中；不考虑轨道结构影响时其值为10.6 MPa，为拉应力，发生在连续梁拱组合桥梁端。

图6　温度荷载下主梁应力

图7为列车竖向荷载作用下主梁应力，从图中可以看出，竖向荷载作用时，轨道结构对主梁受力影响很小。单线加载时，考虑轨道结构影响时主梁最大应力为5.9 MPa，不考虑轨道结构影响时为5.8 MPa，双线加载时主梁应力变化趋势与单线加载一致，因此可忽略轨道结构的影响。

图7　列车竖向荷载下主梁应力

列车制动力作用下，主梁最大应力发生在连续梁拱组合桥梁端，如图8所示。单线加载时，考虑轨道结构影响时主梁最大拉应力为4.7 MPa，压应力为4.0 MPa；不考虑轨道结构时最大拉应力为5.4 MPa，压应力为4.7 MPa。双线加载时，主梁应力变化趋势与单线加载时一致。由于轨道将部分制动力传递到相邻桥梁，因此考虑轨道结构影响时主梁应力较不考虑轨道时小。

图8　列车制动力下主梁应力

3.2梁端转角

在列车竖向荷载的作用下，连续梁拱组合桥梁端会发生转角位移，这对钢轨受力及行车舒适性有一定影响，因此有必要探讨轨道作用对梁端转角的影响。有无轨道结构下梁端转角的比较见表1。

表1　梁端转角比较

从表1可以看出，梁端转角均小于2‰，满足规范要求，考虑轨道结构影响时梁端转角较不考虑轨道结构时小，这是由于轨道对桥梁变形有一定约束作用，因此设计时不考虑轨道结构影响对梁端转角而言是偏安全的。

3.3墩底纵向反力

梁轨相互作用纵向力既存在于钢轨中，也表现在桥墩的纵向受力上，因此有必要探讨墩底纵向反力的变化。

温度荷载作用下，考虑轨道结构影响时最大墩底纵向反力发生在主桥边墩4号墩处，其值为1 972.8 kN，而不考虑轨道结构影响时只有主墩产生纵向反力，其中6号主墩墩底纵向反力较有轨道作用时大29.0%。见图9。

图10为单线加载时墩底纵向反力，与温度荷载作用相似，不考虑轨道结构时只在主墩产生纵向反力，其中6号主墩墩底纵向反力较有轨道作用时大1.5%。无论是否考虑轨道结构的影响，最大墩底纵向反力均发生在主墩。

图11为单线制动时墩底纵向反力，无论是否考虑轨道结构的影响，各墩墩底均产生纵向反力，墩底纵向反力最大值均发生在4号墩，当考虑轨道结构的影响时其值较不考虑时大52.8%。

图11　列车制动力下墩底纵向反力

4　结论

(1)由于本桥跨度较大，温度作用下钢轨伸缩力较大，在连续梁拱组合桥梁端最大伸缩压应力达到114.0 MPa，列车竖向荷载和制动力作用下，钢轨应力较小，其最大值分别为6.6 MPa和16.3 MPa。

(2)经检算，对于该大跨度连续梁拱组合桥，梁端不设钢轨伸缩调节器时，钢轨强度满足要求。

(3)在温度荷载及制动力作用下，主梁应力受轨道作用的影响较大，应当予以考虑。

(4)由于轨道对桥梁变形有一定约束作用，考虑轨道结构影响时梁端转角比不考虑时小，因此桥梁设计中不考虑轨道对梁端转角而言偏安全。

(5)轨道结构对桥墩墩底纵向反力的分配产生一定影响，其中考虑轨道结构影响时，在温度荷载作用下，主桥边墩4号墩墩底纵向反力达到1 972.8 kN，而不考虑轨道结构时该墩墩底不产生纵向反力。

[1]闫斌.高速铁路中小跨度桥梁与轨道相互作用研究[D].长沙：中南大学，2013.

[2]孔文斌，雷春燕.高速铁路长大桥梁无缝线路附加挠曲力计算分析[J].华东交通大学学报，2011，28(1)：25-28.

[3]阴存欣.铁路桥梁纵向附加力的静动力非线性分析与仿真研究[D].北京:铁道部科学研究院， 2000.

[4]朱彬.大跨度钢箱混合梁斜拉桥无缝线路设计研究[J].铁道标准设计，2012(2)：4-6.

[5]刘文硕.高速铁路大跨度钢桁拱桥梁轨相互作用研究[D].长沙：中南大学，2013.

[6]徐庆元，陈秀方，周小林，等.高速铁路桥上无缝线路力学计算模型对比[J].交通运输工程学报，2005，5(3):19-24.

[7]李艳.大跨斜拉桥上无缝线路纵向力的变化规律研究[J].铁道工程学报，2012(10)：42-46.

[8]闫斌，刘从新，杜凯，等.门式墩上高速铁路连续梁桥梁轨相互作用[J].华中科技大学学报:自然科学版，2012，40(3):81-84.

[9]王晴.大跨度曲线连续梁桥与轨道相互作用[D].长沙:中南大学，2014.

[10]闫斌，戴公连.高速铁路斜拉桥上无缝线路纵向力研究[J].铁道学报，2012，34(3):83-87.

[11]卜一之.高速铁路桥梁纵向力传递机理研究[D].成都：西南交通大学土木工程学院，1998.

[12]徐庆元，陈秀方.连续梁桥上无缝线路附加力研究[J].中国铁道科学，2003，24(3):58-62.

[13]李东昇，李学斌，刘文荐，等.国内外关于铁路桥梁列车制动力率取值的差异分析[C]∥第二十届全国桥梁学术会议论文集(上册)，2012：216-220.

[14]中铁第四勘察设计院集团有限公司.TB10015—2012铁路无缝线路设计规范[S].北京：中国铁道出版社，2013.

[15] 赵卫华.斜拉桥上无缝线路设计计算方法研究[D].成都：西南交通大学，2010.

Track-bridge Interaction of Combination Bridge with Long-span Continuous Beam Arch

WANG Wei-min

(China Railway Siyuan Survey And Design Group Co.， Ltd.， Wuhan 430063， China)

To study the characteristics of track-beam interaction of the combination bridge with long-span continuous beam arch， a rigid frame arch combination bridge with (34+160+34) m continuous steel-box girder tied-arch on Meizhou-Chaoshan railway line is referenced. A track-arch-beam-pier integration space model is established to simulate track longitudinal resistance with ideal elastic-plastic model. The distribution of track longitudinal force is analyzed. The girder stress， the rotation angle at bridge end， and the longitudinal reaction at pier bottom are compared with or without track effects. Results show that rail longitudinal force is great at the beam end farther away from the fixed support of the combination bridge with continuous beam arch; the maximum expansion stress reaches to 114.0 MPa， but the rail strength meets the requirements without rail expansion devices; the track structure has great impact on the stress of girder under the action of temperature load or braking force and it also has great impact on rotation angle at bridge end and on the distribution of longitudinal reaction at pier bottom．

Combination bridge with continuous beam arch; Track longitudinal force; Track effect; Stress of girder; Rotation angle at bridge end; Longitudinal reaction at pier bottom

2016-03-02；

2016-03-09

王伟民(1989—)，男，助理工程师，2015年毕业于中南大学土木工程学院桥梁与隧道工程专业，工学硕士，主要从事桥梁工程设计与研究工作，E-mail：756926496@qq.com。

1004-2954(2016)09-0079-04

U441+.7

ADOI:10.13238/j.issn.1004-2954.2016.09.018