非线性三阶三点边值问题的拟上下解方法*

韩如霞

（河北工业大学理学院，天津，300401）

非线性三阶三点边值问题的拟上下解方法*

韩如霞

（河北工业大学理学院，天津，300401）

通过构造拟上下解的单调迭代过程，在拟解对之间利用Sadvoskii不动点定理获得了Banach空间非线性三阶三点边值问题解的存在性.

拟上下解对 非紧性测度 凝聚映射 Sadvoskii不动点定理

1　引言

考虑非线性三阶三点边值问题

上下解方法和单调迭代技巧是研究微分方程初边值问题的有力工具，其优点是不但能得到解的存在性，而且能得到求解的迭代过程.拟上下解方法则是上下解方法的推广，自从V. Lakshmikantham等提出拟上下解的概念，并通过拟上下解对的混合单调迭代序列获得了一阶常微分方程u′=f（t，u）的初值问题的拟解对的存在性［1-2］，随后人们开始了用拟上下解方法对微分方程解的存在性的研究，2001年，李永祥对Banach空间内一阶常微分方程的初边值问题运用一种拟上下解方法证明其解的存在性［3］；2005年，刘旭对Banach空间内的二阶边值问题运用拟上下解方法证明了其解的存在性［4］；2013年，李强对Banach空间中一类二阶三点边值问题运用拟上下解方法证明了其解的存在性［5］.受此上的启发，本文在紧型条件下，通过非紧性测度的精巧计算，利用拟上下解单调迭代方法及Sadvoskii不动点定理讨论了非线性三阶三点边值问题（1）拟解对的存在性及其拟解对之间解的存在性.

2　预备知识

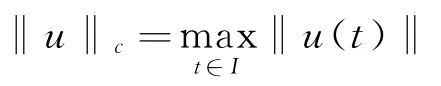
定义2.1［7］设E是实Banach空间，S是E中的有界集.

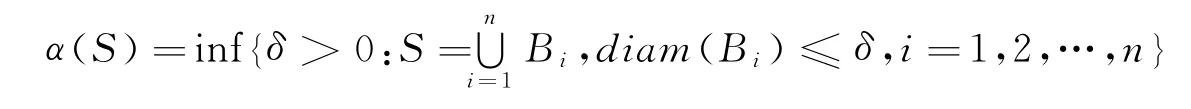
称为集合S 的Kuratowski非紧性测度，其中diam（Bi）表示集合Bi的直径.

显然，0≤α（S）≤+∞.

引理2.1［6］若βη≠1，则对y∈C［0，1］，边值问题

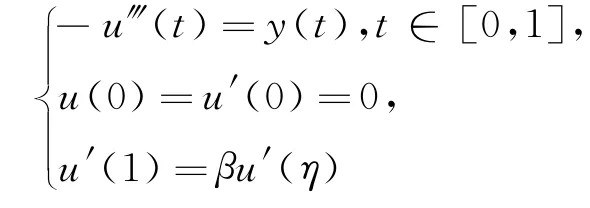
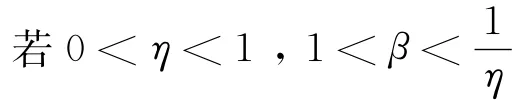
证明 由T的定义得.

显然，Tn：C［I，E］→C［I，E］是正有界线性算子.

由范数的定义和格林函数的性质有

又因为

引理2.4［7］设E是实Banach空间，S 是E中的有界集，则α（S）=0的充要条件是S 是相对紧集.

引理2.5［7］若B⊂C［I，E］等度连续且有界，则

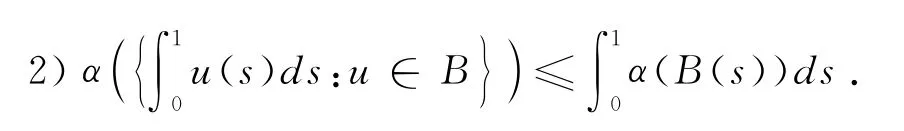
引理2.6［8］若B=un｛｝⊂C［I，E］有界，则有

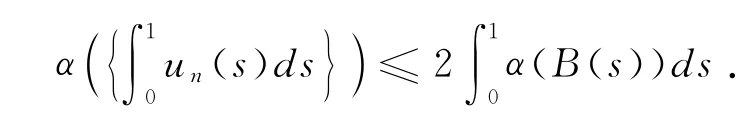
引理2.7［9］若有界，则存在可列子集，使得.

引理2.8［4］若等度连续，则等度连续.

引理2.9（Sadvoskii）［10］设D是E中有界凸闭集（D不一定有内点），A：D→D是凝聚映象，则A在D中必有不动点.

定义2.2［10］设E1，E2是Banach空间，D ⊂E1.设A：D →E2连续且有界.如果存在常数k≥0，使对任何有界集S⊂D，都满足α（A（S））≤kα（S），则称A是D上的k-集压缩映象.特别地，k＜1时的k-集压缩映象称为严格集压缩映象.如果对任何非相对紧的有界集S⊂D，都满足α（A（S））≤α（S），则称A是D上的凝聚映象.

显然，严格集压缩映象必为凝聚映象.

定义2.3 若v0，w0∈C3［I，E］满足条件

则称v0，w0为边值问题（1）的一对拟上下解；若上述式子均取等号，则称v0，w0为边值问题（1）的拟解对.

3　主要结果及证明

定理3.1 设E 为有序Banach空间，P为E中正规锥.若边值问题（1）存在拟上下解对v0，w0∈C3［I，E］，使得v0≤w0，且f（t，x，y）：I×E×E→E连续，在［v0，w0］上满足：

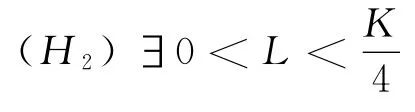
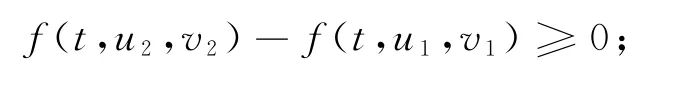
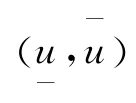
证明 （I）证明拟解对的存在性

对∀h1，h2∈［v0，w0］，考虑E中三阶边值问题

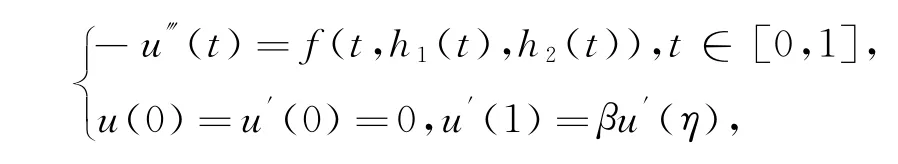
由引理2.1可知，存在唯一解

①显然，算子A：［v0，w0］×［v0，w0］→C［I，E］连续，且方程（1）的解等价于算子A的不动点u=A（u，u）.

②由条件（H1）以及格林函数G（t，s）≥0可知，算子A：［v0，w0］×［v0，w0］→C［I，E］为混合单调算子.

③下证：v0≤A（v0，w0），A（v0，w0）≤w0.

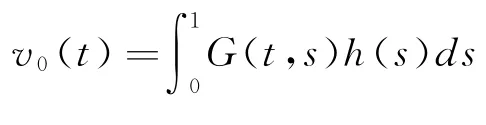
④作迭代序列vn=A（vn-1，wn-1），wn=（wn-1，vn-1），n=1，2，….

由A是混合单调算子，有

下证vn｛｝，wn｛｝收敛.

令B1=vn｛｝，B2=wn｛｝，D=B1∪B2，则B1，B2等度连续且有界.由引理2.5，引理2.6，条件（H2）及非紧性测度的性质，可得令α（D t（））=φ（t），则φ（t）≤4LTφ（t）.累次使用上述不等式，可得φ（t）≤（4L）nTnφ（t）.两边取范数即得‖φ（t）‖≤（4L）n‖Tn‖‖φ（t）‖.

下证：Q是凝聚映象.

对任意有界集B⊂Ω0，B，QB（）等度连续且有界.根据引理2.5，引理2.6，引理2.7，条件（H2）及非紧测度性质，可知存在可列子集B0⊂B使得

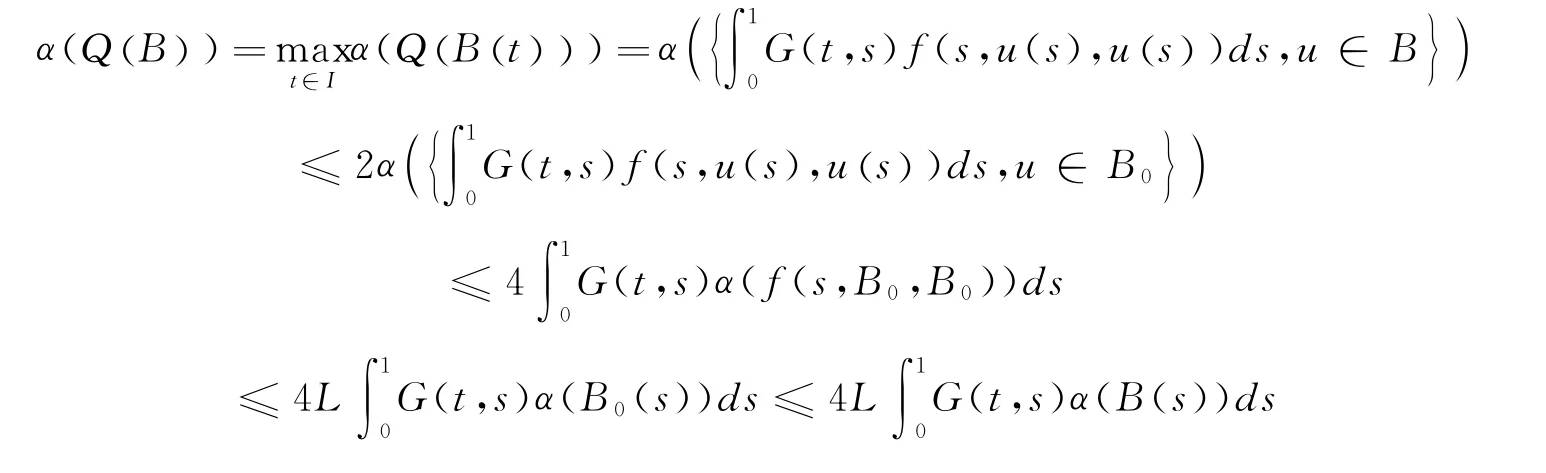
［1］Lakshmikantham V，Leela S，Vatsala A S.Method of quasi-upper and lower solutions in abstract cones［J］.Nonlinear Anal，1982，6：833-838.

［2］Guo Dajun，LakshmikanthamV.Coupled fixed points of nonlinear operator with applications［J］. Nonlinear Anal，1987，11：623-632.

［3］李永祥.Banach空间常微分方程的一种拟上下解［J］.西北师范大学学报，2001，37（3）：6-11.

［4］刘旭.Banach空间二阶边值问题的拟上下解方法［J］.西北师范大学学报，2005，41（2）：4-7.

［5］李强.Banach空间中一类二阶三点边值问题的一种拟上下解［J］.河南师范大学学报，2013，41（1），15-18.

［6］郭丽君.非线性三阶三点边值问题的正解［D］.收藏地：中国知网，2008.6.4.

［7］郭大钧.孙经先.抽象空间常微分方程［M］.济南：山东科学技术出版社，1989.

［8］Hein H R.On the behavior of noncompactness with respect to differentiation and integration of vectorvalued function［J］.Nonlinear analysis（TMA），1983，7：1351-1373.

［9］李永祥.抽象半线性发展方程初值问题解的存在性［J］.数学学报，2005，48（6）：1089-1094.

［10］郭大钧.非线性泛函分析［M］.济南：山东科学技术出版社，1985.

Quasi-Upper and Lower Solutions of Nonlinear Third-order Three-point Boundary Value Problem

Han Ruxia
（College of Science，Hebei University of Technology，Tianjin 300401，China）

By employing the Sadvoskii fixed point theorem and constructing the monotone iterative process of the quasi-upper and lower solutions，the existence of solutions between quasi-solutions is obtained for nonlinear third order three point boundary value problems in Banach spaces.

Quasi-upper and lower solutions Measure of noncompactness Condensing map Sadvoskii fixed point theorem

2016年02月17日