两类稳定性定理的改进*

范英飞 黄倩倩 杨墨

（西南交通大学数学学院，成都，611756）

两类稳定性定理的改进*

范英飞 黄倩倩 杨墨

（西南交通大学数学学院，成都，611756）

本文研究两类稳定性定理.对LaSalle不变原理做更加合理的改进.研究了Lyapunov直接法，得到了改进的比较原理，并加以证明，最后应用到实例中.

LaSalle不变原理 比较原理 改进

1　LaSalle不变原理

1960年，LaSalle［1］发现了Lyapunov函数与伯劳霍夫极限集［2］之间的关系，对函数的直接法进行了推广.实际上考察一个运动极限集位置的研究，就是考察该运动的渐进行为，因此我们可以选定适当的Lyapunov函数，利用极限集的不变性，给出极限集位置的信息.这一思想称为“不变原理”.LaSalle不变原理在多个领域中具有广泛的应用，例如在Multi-Agent系统［3］和线性切换系统［4］.

鉴于定理的实用性，许多学者对这一原理进行了深入的讨论和研究［5-8］.本节旨在对La-Salle不变原理做更加合理的改进，降低其使用的难度.

1.1n维自治系统

考虑n维自治系统

其中x=col（x1，x2，…xn），f=col（f1，f2，…fn），f：D∈Rn→Rn连续，0∈D保证（1）的解的唯一性.

称x*∈D为正半轨线x（tk，t0，x0）的ω极限点，若有序列tk｛｝满足

记Ω（x0）为起始点x0的所有ω极限点x*组成的集合.

区域D的边界记为∂D.

1.2LaSalle不变原理的改进

定理1 设D是一个有界闭集，（1）的解的起始点x0⊂D.若∃V（x）：D→R为Lyapunov函数，具有一阶连续偏导数，且有则区域D为（1）的解的不变集.

若不然，由连续函数的介值定理，必存在t2＞t1＞0，使得x（t1，t0，x0）为∂D上一点，x（t2，t0，x0）为跃出边界的轨线上一点，且有x（t2，t0，x0）＞x（t1，t0，x0）.

因为V（x）是严格单增的函数，容易得到

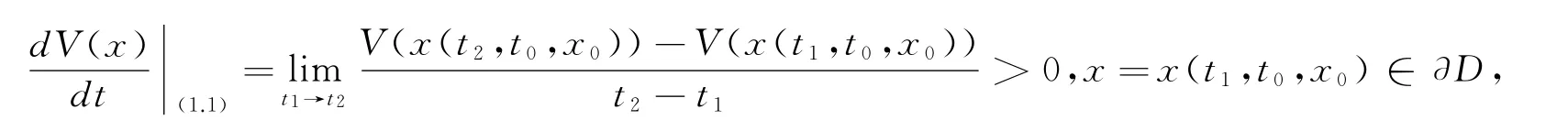
显然这与假设矛盾.因此x（t，t0，x0）⊂D必然成立，区域D为（1）的解的不变集.定理得证.

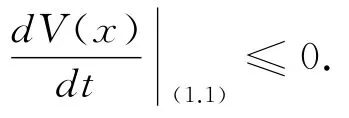
1.3例子

例 用极限环的情形来应用上述定理.

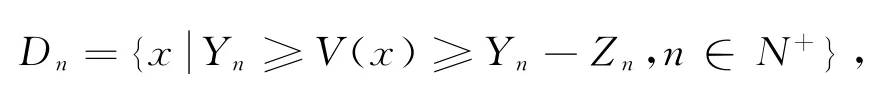
使得

那么在区域D内的环形区域Dn被叫做极限环.

2　比较原理

Lyapunov直接法的许多定理及推广，解决了很多的实际问题［9-10］，但对于一些比较复杂的问题，必须结合其他方法加以处理，其中理论上最完善，应用上最广泛的便是比较原理［11-14］.

2.1预备知识

首先给出比较原理的思想实质.

考虑n维非自治系统

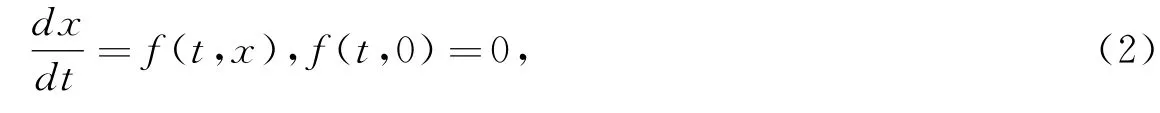
其中x=col（x1，x2，…xn），f=col（f1，f2，…fn），f连续，保证（2）的解的唯一性.

同时再给定一个纯量方程

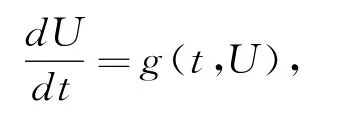
其中g（t，0）≡0，g ∈C［I×Rn，R+］.

设存在正定函数V（t，x），关于x 满足局部Lipschitz条件，V（t，0）≡0，且有

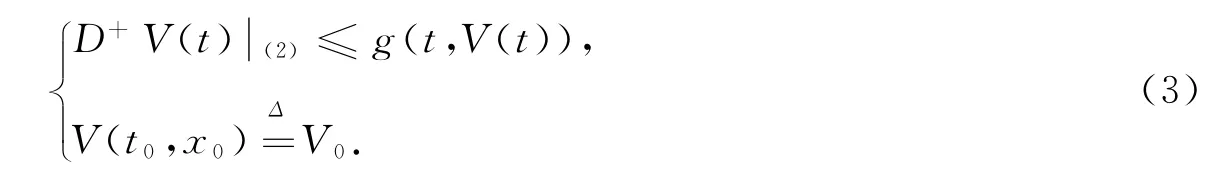
再考虑比较方程

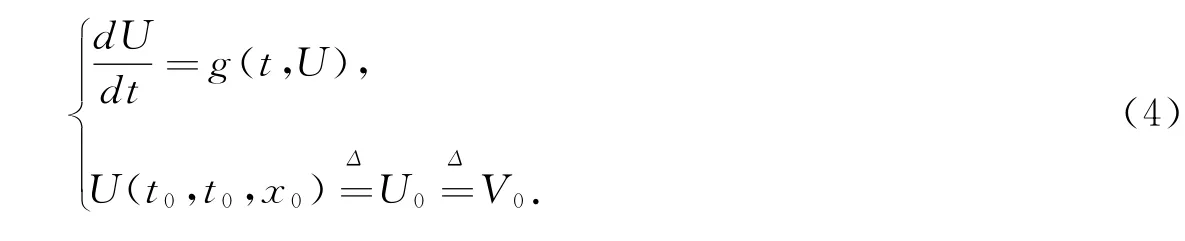
根据（2），（3），可得

因此我们可以通过（3）的解的稳定性来判断（2）的解的稳定性.

2.2比较原理的改进

定理2 若存在Lyapunov函数V（t，x）∈C［I×Rn，R+］，关于x满足Lipschitz条件，V（t，0）≡0，且V沿（2）解的右上Dini导数［15］满足

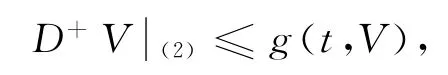
则（3）的平凡解一致稳定蕴涵（2）的平凡解一致稳定.

证明 因为V正定，由定义知∃φ∈K［2］，使得

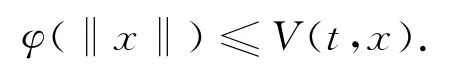
因为（2.3）的平凡解一致稳定，由定义知∀ε＞0，∃δ（ε），只要U0＜δ（ε），就有

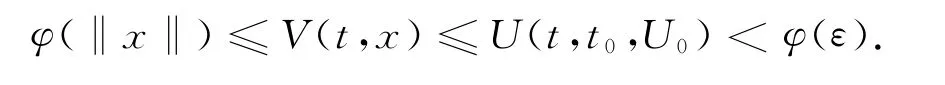
因此

再根据

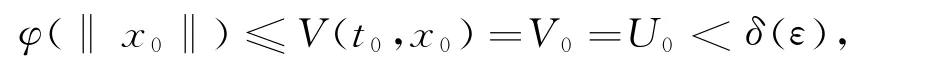
可得

所以∀ε＞0，∃δ1（ε）＞0，当‖x0‖＜δ1（ε）时，有‖x‖＜ε，即（2.4）的平凡解一致稳定.定理2得证.

注 原始的比较原理［16］，V还需要满足具有无穷小上界这一条件.

2.3例子

再给定方程组

我们验证了定理2的可行性.

3　小结

改进后的比较原理，我们去掉了V函数具有无穷小上界这个条件，从而提高了实用效率.

［1］LaSalle.J.P.动力系统的稳定性［M］.廖晓昕等译.武汉：华中理工大学出版社，1988.

［2］廖晓昕.稳定性的理论，方法和应用［M］.武汉：华中科技大学出版社，2005.

［3］Daizhan Cheng.An extension of LaSalle’s invariance principle and Its application to multi-agent consensus［J］.IEEE Transactions on Automatic Control，2008，8：1765-1770.

［4］Hespanha.J.P.Uniform stability of switched linear systems：extensions of LaSalle Invariance Principle［J］. IEEE Transactions on Automatic Control，2004，4：470-482.

［5］赖定文.关于稳定性定理的一点补充［J］.科学通报，1984，19：1161-1163.

［6］Shujun Long，Daoyi Xu and Wei Zhu.Global exponential stability of impulsive dynamical systems with distributed delays［J］.Electronic Journal of Quanlitative Theory of Differential Equations，2007，10：1-13.

［7］Massera.J.L.On Lyapunov condition of stability［J］.Analysis of Mathematics，1949，50：34-42.

［8］徐道义.关于稳定性的几个基本定理［J］.数学季刊，1992，7，2：61-67.

［9］Rouche.N.Habets and P，Laloy M.Stability theory by Lyapunov，Direct method［J］.Springer-Verlag，1977，32：134-147.

［10］Bhatia.N.P.and Szego.G.P.Stability Theory of Dynamical Systems［M］.Berlin：Springer-Verlag Berlin，1988.

［11］张彩虹，高存臣.比较原理在多有理数时滞区间系数离散系统的应用［J］.中国海洋大学学报，2006，36：219-221.

［12］罗交晚，邹捷中，侯振挺.比较原理与Markov调制的随机时滞系统的稳定性［J］.中国科学，2003，33：374-381.

［13］Zhang H G，Wang G.New criteria of global exponential stability for a class of generalized neural networks with time-varying delays［J］.Neurocomputing，2007，70：2486-2494.

［14］丛伟，潘贞存，赵建国.基于纵联比较原理的广域继电保护算法研究［J］.中国电机工程学报，2006，21：8-14.

［15］Yoshizawa.T.Stability Theory by Lyapunovs Second Method［J］.The math science of Japan，1996，18：102-109.

［16］尤秉礼.常微分方程补充数据［M］.北京：人民教育出版社，1983.

Two Types of Improved Stability Theorems

Fan Yingfei Fan Xiaoming Huang Qianqian Yang Mo
（School of Mathematics，Southwest Jiaotong University，Chengdu 611756，China）

In this paper we give improvements to the LaSalle invariance principle and the comparison principle，and then apply them to examples.

LaSalle invariance principle Comparison principle Improvement

2016年03月17日