Young不等式的一种推广

吴淑君，石忠锐

（1.上海大学理学院，上海 200444；2.中国石油大学（华东）基础数学系，山东青岛 266580）

Young不等式的一种推广

吴淑君1，2，石忠锐1

（1.上海大学理学院，上海 200444；2.中国石油大学（华东）基础数学系，山东青岛 266580）

首先修正了专著《Orlicz空间几何理论》中的定理1.10,对修正后的结果给出了严格的数学证明,借助此结果证明了一类推广的Young不等式,从而完善了Young不等式的理论体系.

Young不等式；N-函数；右反函数

1912 年，Young［1］证明了著名的Young不等式：

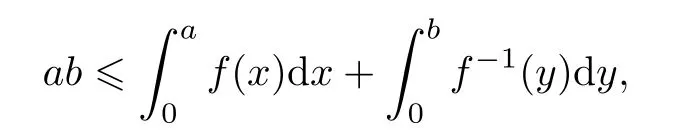
式中，f为严格递增的连续函数，等号成立当且仅当b=f（a）.Young不等式不仅是数学分析中的重要不等式［2-3］，而且还广泛应用于逼近论［4］、矩阵分析［5］等学科.由于f的单调性和连续性限制了Young不等式的使用范围，人们研究了Young不等式的各种推广，如关于非减连续函数的Oppenheim不等式［3］、关于多元可微函数的不等式［3］等.

如果f是非减的右连续函数，则虽然不满足Young不等式，但此时f的原函数是凸函数.借鉴Jensen［6］对凸函数的研究成果，文献［7］给出了Young不等式的一种推广：

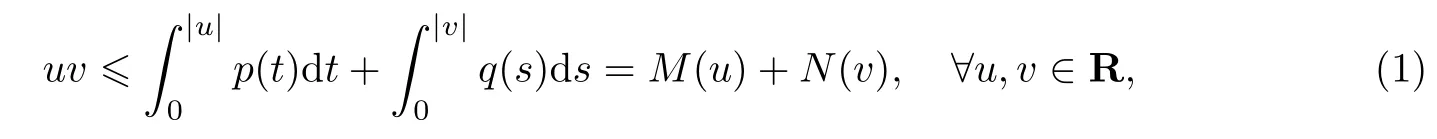
式中，p为右连续的非减函数，q为p的右反函数，等号成立当且仅当p-（|u|）6|v|6 p（|u|）.此式将Young不等式向前推进了一大步，使得一大类函数纳入了Young不等式的范畴，由此一些经典结论得到了推广，如LP中的H¨older不等式、Minkowski不等式等［2-3］.近年来，Orlicz空间给众多非线性问题提供了恰如其分的空间框架，特别是在图像处理、电流变流体、非线性弹性力学等热门领域中展现出了LP空间所不能及的优势［8-9］.Orlicz空间正是式（1）中的凸函数M生成的，并且此不等式是研究Orlicz空间的支柱工具［7,10-13］.目前所见文献中只对此不等式给出了几何解释，并未见严格的数学证明.Luo等［14］试图利用文献［11］中的定理1.10（即文献［10］中的引理1.14）作为主要工具来证明此不等式，但是此定理不真.

本研究首先修正了文献［11］中的定理1.10，并给出修正后结果的严格数学证明，然后借助经典Young不等式证明了推广后的不等式（1），从而完善了Young不等式的理论体系.

1 预备知识

定义1［7］称M：R→［0,∞）是一个N-函数是指M是偶的凸函数，并且满足

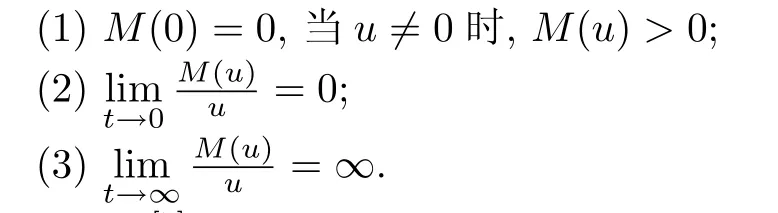
引理1［7］M：R→［0,∞）是一个N-函数当且仅当存在定义于［0,∞）的函数p满足

（1）p是右连续的非减函数；

（2）当t＞0时，p（t）＞0；

（3）p（0）=0，p（∞）=∞，

定义2［7］q（s）=sup｛t0：p（t）s｝称为p的右反函数，称为M的余函数.

注1［7］p，q互为右反函数，M,N互为余函数.p，q满足q（p（u））u,p（q（u））u,u∈［0,∞）.

定义3［10］称区间［a,b］是函数M的结构仿射区间（structural affine interval，SAI），如果M在［a,b］上仿射，且∀η＞0,则M在［a-η,b+η］上不仿射.

定义4［7］称函数M：R→R是严格凸的是指

引理3［7］N-函数M严格凸⇔M的右导数p严格递增⇔p的右反函数q连续.

2 主要结果

引理4 对任意的N-函数M，以及任意ε＞0，存在严格凸的N-函数Mε，使得

式中，p,pε分别为M,Mε的右导数.

证明 如果p是右连续的非减函数，且p（∞）=∞,则p为常数的区间必为［ak,bk）形的.记这种区间的全体是当k不同时，［ak,bk）互不相交且为结构仿射区间（SAI）.

（1）证明对任意的ε∈（0,1）都存在满足式（2）的函数pε（t）,t∈［0,∞）.

步骤1 令S1=［a1,b1）,分成以下两种情况讨论.

情况1 p（b1）＞p（a1）.

从而，pε（t）在上满足式（2）.

情况2 p（b1）=p（a1）.

由于p在b1处右连续，故取使得令在上定义pε（t）为过的直线段.下证pε（t）在上满足式（2）.

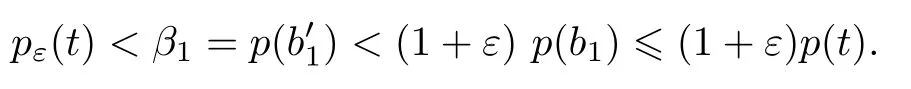
从而pε（t）在上满足式（2）.

步骤2.1 S2=φ,同步骤1处理.

情况1 如果S2⊂（-∞,a1）,则这与矛盾.

1）如果S2=［a2,b2）,则令根据步骤1，pε在上已有定义且满足式（2）.

步骤3.1 S3=φ,同步骤1处理.

1）如果S3=［a3,b3），则存在i0∈｛1,2｝,使得同步骤2的情况2讨论.

……

步骤k.1 Sk=φ,同步骤1处理.

1）如果Sk=［ak,bk），则存在i0∈｛1,2,…,k-1｝,使得令同步骤2的情况2讨论.

……

（2）证明pε在［0,∞）上严格递增.

1）存在k1,使得根据pε的构造可知

2）存在k2,k3,且使得由于故从而即

注2 文献［11］中定理1.10的证明方法不真.反例如下：

定理1 对任意的u,v∈R,都有

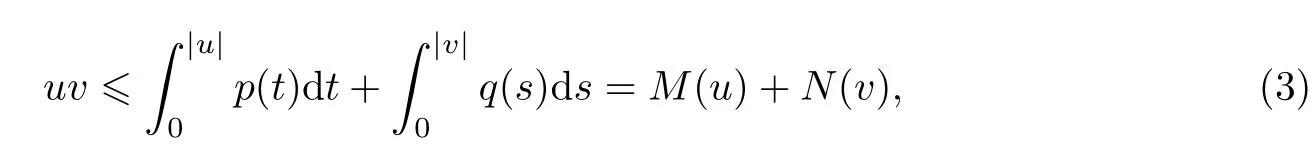
等号成立当且仅当p-（|u|）|v|p（|u|）.

证明 因为M,N是偶函数，所以只需证明u＞0,v＞0时结论成立.

由于pε严格递增，故由引理3知qε连续.再由引理4，存在一个严格递增的连续函数qεε，并满足

联合式（4）和（5）可得

由于qεε是严格递增的连续函数，故qεε的右反函数pεε与qεε互为反函数，且仍为严格递增的连续函数.根据pεε的定义知

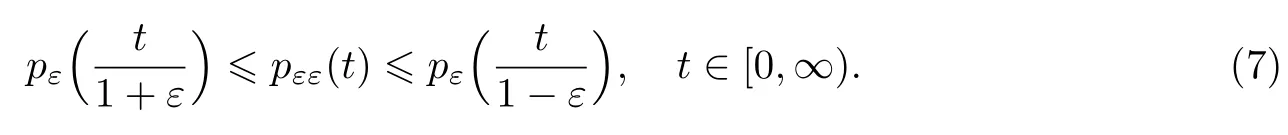
由式（3）和（7）得

由经典Young不等式得

当且仅当v=pεε（u）时等号成立.

根据式（8），有

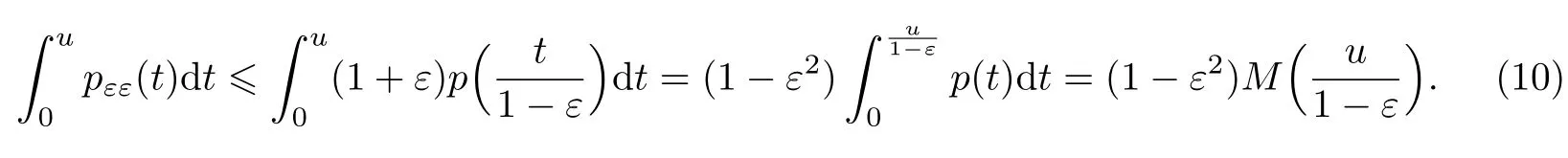
再根据式（6）得

联合式（9）～（11），有

下面证明式（1）中等号成立当且仅当p-（u）vp（u）.

（1）充分性.

首先说明up（u）=M（u）+N（p（u））.

∀ε＞0,根据式（8）以及Young不等式中等号成立的条件可得

由式（8），（10）和（11）知

另一方面，∀w＞u＞0,由式（8）和Young不等式中等号成立的条件知

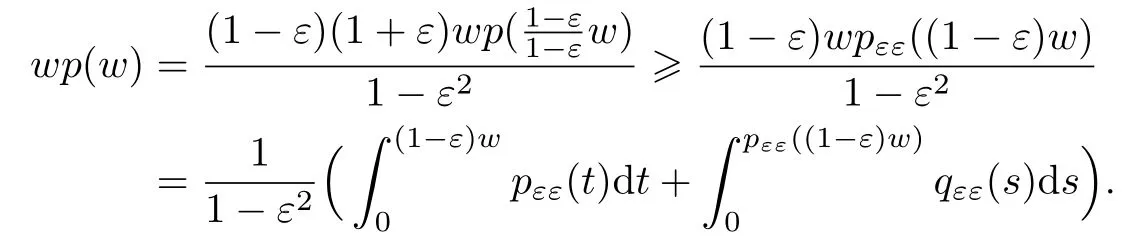
并且，

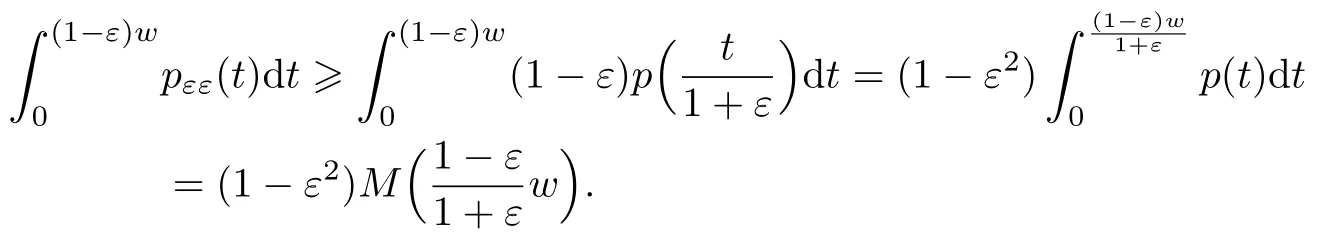
根据式（6）和（8），

当u=q（v）时，根据对称性知

∀v∈［p-（u）,p（u）］，

1）当p-（u）=p（u）时，v=p（u）,从而uv=M（u）+N（v）.

2）当p-（u）＜p（u）时，∀v∈［p-（u）,p（u））有q（v）=sup｛s0：p（s）v｝=u,故uv=M（u）+N（v）.

（2）必要性.

如果uv=M（u）+N（v），则v∈［p-（u）,p（u）］；

反之，则存在u＞0,v∈（0,p-（u））S（p（u）,∞）,满足uv=M（u）+N（v）.

1）如果存在t0∈（p（u）,v）,使得q（t0）＞q（p（u））u.根据q是右连续的非减函数，有

因此M（u）+N（v）＞uv，这与uv=M（u）+N（v）矛盾.

2）如果∀t∈［p（u）,v）,有q（t）=q（p（u））=q-（v）＞u,则

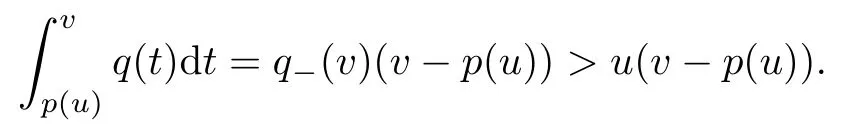
故M（u）+N（v）＞uv,矛盾.

当v＜p-（u）时，有q（v）＜u.根据u与v，p与q的对称性可得M（u）+N（v）＞uv，矛盾.

注3 根据对称性，有式（1）中等号成立当且仅当q-（|v|）6|u|6 q（|v|）.

［1］YOUNG W H.On classes of summable functions and their Fourier series［J］.Proc Royal Soc（A）, 1912,87：225-229.

［2］HARDY G，LITTLEWOOD J E,P´OLYA G.Inequalities［M］.2nd ed.Cambridge：Cambridge University Press,1952：70-101.

［3］匡继昌.常用不等式［M］.3版.济南：山东科学技术出版社,2004：136-138.

［4］CHENEY E W.Introduction to approximation theory［M］.New York：McGraw-Hill,1996：231-235.

［5］HIRZALLAH O，KITTANEH F.Matrix Young inequalities for the Hilbert-Schmidt norm［J］.Linear Algebra and Its Applications,2000,308（1/2/3）：77-84.

［6］JENSEN J L W V.Sur les functios convexes et les in´egalit´es entre les valeurs moyennes［J］.Acta Math,1906,30：175-193.

［7］KRASNOSELSKI M，RUTICKII Y.Convex functions and Orlicz space［M］.Noordhoff：Groningen, 1961：1-23.

［8］CHENY，LEVINES，RAO M.Variable exponent,linear growth functionals in image restoration［J］.SIAM J Appl Math,2006,66（4）：1383-1406.

［9］HALSEY T C.Electrorheological fluids［J］.Science,1992,258：761-766.

［10］CHEN S T.Geometry of Orlicz spaces［M］.Warszawa：Dissertationes Math,1996：1-13.

［11］吴从炘,王廷辅,陈述涛,等.Orlicz空间几何理论［M］.哈尔滨：哈尔滨工业大学出版社,1986：1-30.

［12］SHI Z R，LIU C Y.Noncreasy and uniformly noncreasy Orlicz-Bochner function spaces［J］. Nonlinear Anal,2011,74：6153-6161.

［13］LIU C Y，SHI Z R.Notes of k-smoothness in Orlicz sequence spaces［J］.J Shanghai Univ（Engl Ed）,2010,14（6）：420-423.

［14］LUO X Q，XIONG Z P.A kind of extension of the famous Young inequality［J］.Journal of Inequalities and Applications,2013,437：1-11.

A class of extension of the Young inequality

WU Shujun1,2，SHI Zhongrui1
（1.College of Sciences，Shanghai University，Shanghai 200444，China；
2.Department of Basic Mathematics，China University of Petroleum，Qingdao 266580，Shandong，China）

The proof of a revise for Theorem 1.10 in Geometry of Orlicz Spaces is presented.A class of extension of the Young inequality is then established based on the revision to improve the Young inequality.

Young inequality；N-function；right-inverse function

O 178

A

1007-2861（2016）04-0461-08

10.3969/j.issn.1007-2861.2015.01.014

2014-12-01

国家自然科学基金资助项目（11271245）

吴淑君（1981—），女，博士，研究方向为空间理论.E-mail：wushujun1981@163.com