模袋砂堤防沉降量预测的分数阶灰色模型

李　倩,周星德,周子言

(1. 河海大学土木与交通学院,江苏 南京　210098;2. 河海大学文天学院,安徽 马鞍山　243031)



模袋砂堤防沉降量预测的分数阶灰色模型

李倩1,周星德1,周子言2

(1. 河海大学土木与交通学院,江苏 南京210098;2. 河海大学文天学院,安徽 马鞍山243031)

为获得更优的模袋砂堤防沉降预测结果,基于灰色模型,提出一种分数阶灰色模型。运用MATLAB语言编写了相关程序,实现微分阶次到分数阶的改变,并运用该模型对模袋砂滩涂围垦测试的沉降结果进行实例分析。分数阶灰色模型与灰色Verhulst模型、残差GM模型、GM(1，1)模型对比分析表明:(a)分数阶灰色模型预测结果更精确,其不仅具有GM(1,1)模型前期预测效果好的优点,而且具有灰色Verhulst模型后期预测效果好的优点;(b)分数阶灰色模型的中长期预测结果稳定性比残差GM模型好。

模袋砂堤防;沉降量预测;分数阶;灰色模型;灰色Verhulst模型;残差GM模型

海堤工程是海涂围垦中至关重要的一环,海堤工程的成败直接关系到人民生命财产的安全,影响围垦事业的发展。模袋砂多用于临时围堰,随着技术的发展,目前已经出现了采用模袋砂构筑的堤防。海堤多建于软土地基上,为确保地基能在稳定状态下工作,在施工过程中及完工后必须对其进行有效监测和信息反馈。有关地基沉降预测的方法有很多,沉降曲线多符合指数函数[1],而实际测量结果总会产生奇异,对这种现象,分形理论具有较好的处理[2-3];多数预测方法具有分段预测的特点,即间或前期预测好,间或后期预测好,为此出现了组合预测方法[4];目前公认较好的预测方法当属灰色模型[5-7],主要包括GM(1,1)模型[8]、灰色Verhulst模型和残差GM模型[9-10],其中GM(1,1)模型对后期预测效果不好,灰色Verhulst模型对前期预测效果差[11-12]，残差GM模型适用于中长期预测。

从本质上讲,灰色模型采用整数阶导数反映地基的沉降,如:一阶、二阶导数,这是间断的,中间缺少分数,如3/2等,而实际情况千变万化,符合整数阶导数规律的只是其中一小部分情况,因此分数阶模型与实际情况更吻合[13]。基于灰色模型,笔者提出一种分数阶灰色模型,具体过程如下:首先,根据灰色模型算法确定系数项和常数项,变整数阶导数为分数阶导数;其次,通过Laplace变换改为频域表示,假设外激励为由灰色模型所确定的常数项,构造传递函数;再次,采用Oustaloup算法[14]对分数阶进行逼近,通过仿真曲线的走势来确定分数阶的阶次,进而提出采用一个调节因子以达到与测试数据的最佳吻合。最后,基于文献[15]提供的数据,通过GM(1,1)模型、灰色Verhulst模型、残差GM模型及本文方法间的对比分析,验证本文方法的有效性。

1　灰 色 模 型

灰色模型[5-7](GM(1，1)模型)的特点是对沉降前期预测较好,设n个等距时间序列数据为

(1)

式(1)进行一次累加,可得

(2)

其中

x1(k)微分方程模型为

(3)

式中:a——系数项;b——常数项。

式(3)的时间响应序列解为

(4)

改进的灰色模型中,较普遍的2种为灰色Verhulst模型和残差GM模型。灰色Verhulst模型的特点是对沉降后期预测较好,其模型的微分方程为

(5)

(6)

式(5)的时间响应序列解为

(7)

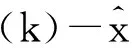
2　分数阶灰色模型

通常使用的导数,如一阶导数、二阶导数,称为整数阶导数,是间断的,中间缺少分数,如3/2阶导数。有关分数阶的研究近年来开始受到重视,这是由于它是连续的,能够更好地反映实际情况[13]。目前有关分数阶的定义有4种,本文采用Riemann-Liouville微积分定义,对于初值为零的β阶导数可表示为

(8)

式中:β——分数,m-1<β≤m;m——临近β的整数;Γ(*)——Gamma函数。

式(5)所表示的模型为整数阶模型,为了扩展其应用范围,可改写为如下分数阶模型:

(9)

假设外激励为常数项b,对式(9)进行Laplace变换,则频域表示为

(10)

采用Oustaloup算法对分数阶进行逼近,拟合频率段为(ωl, ωh),则可构造如下滤波器的传递函数:

(11)

其中

式中:N——整数;2N+1——滤波器的阶次。

用G(s)代替式(10)中的sβ,可得

(12)

其中

ni=2N+1

把式(12)转换为状态方程:

(13)

式中:A、B、C——变换矩阵;X——状态变量;D——系数。

(14)

其中

式中:c——补充的常数, 也称为调节因子

3　实 例 分 析

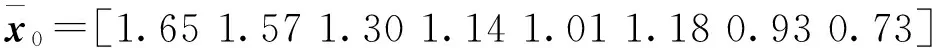
GM(1,1)模型预测序列为

(15)

灰色Verhulst模型预测序列为

(16)

残差GM模型对残差序列进行灰色建模，结果见表1。

采用本文方法,滤波器在频域内近似时,N=4,拟合频率段为[0,1 000](单位:rad/s),通过式(14)可确定调节因子为8,然后通过不断变动分数阶β确定最佳拟合效果,最终确定阶次为0.314 2,即

(17)

由式(11)确定sβ,代入式(12),即可获得的H(s),进而可转换为式(13)表示的状态方程,限于篇幅,这里仅给出状态方程结果:

C=[00.007 30.248 81.646 02.231 10.633 50.037 90.000 50]×106

其中A12=-0.010 7A21为八阶单位矩阵

A11=-[0.000 50.037 60.629 42.224 91.652 20.252 90.007 60]×106

沉降预测结果见表1,从表1可以看出本文预测方法比GM(1，1)模型、灰色Verhulst模型以及残差GM模型要好。

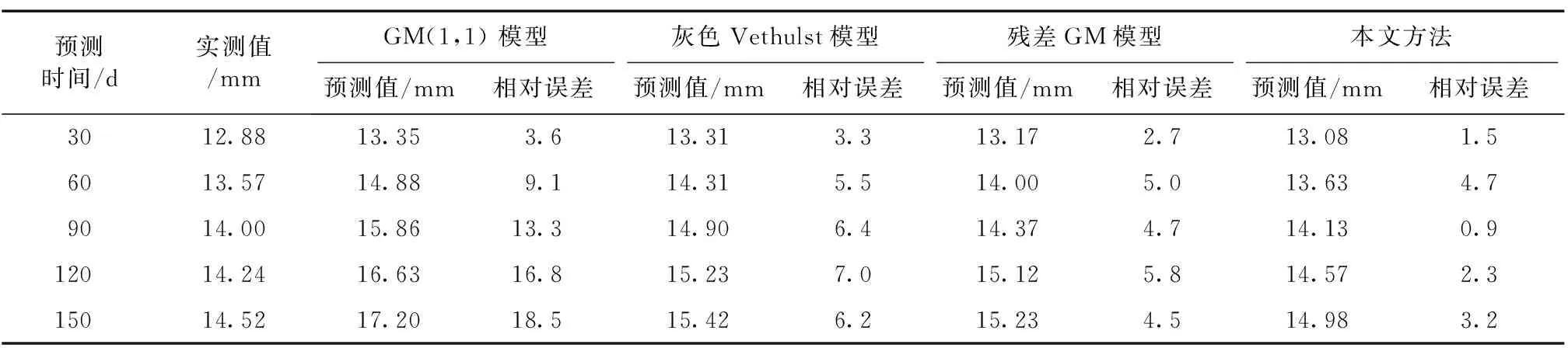
表1　沉降预测结果Table 1　Predicted settlement obtained from different models

2008 年12 月江苏省政府通过了《江苏沿海滩涂围垦开发规划》,2009年6月国务院批准了《江苏沿海开发战略规划》,到2020年形成新围垦面积1 804.77 km2,新筑围海围堤675.28 km,促淤导堤总长177. 05 km。模袋砂围堤类似于模袋围堰,具有用土量少、抗冲刷能力强、施工工艺简单、造价低廉等特点。其基本原理是采用水力吹填的方法将砂水混合物灌入模袋中,砂料在模袋中泌水固结后形成较为密实的填筑体,与模袋组合构筑成定型的围堤。

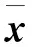
(18)

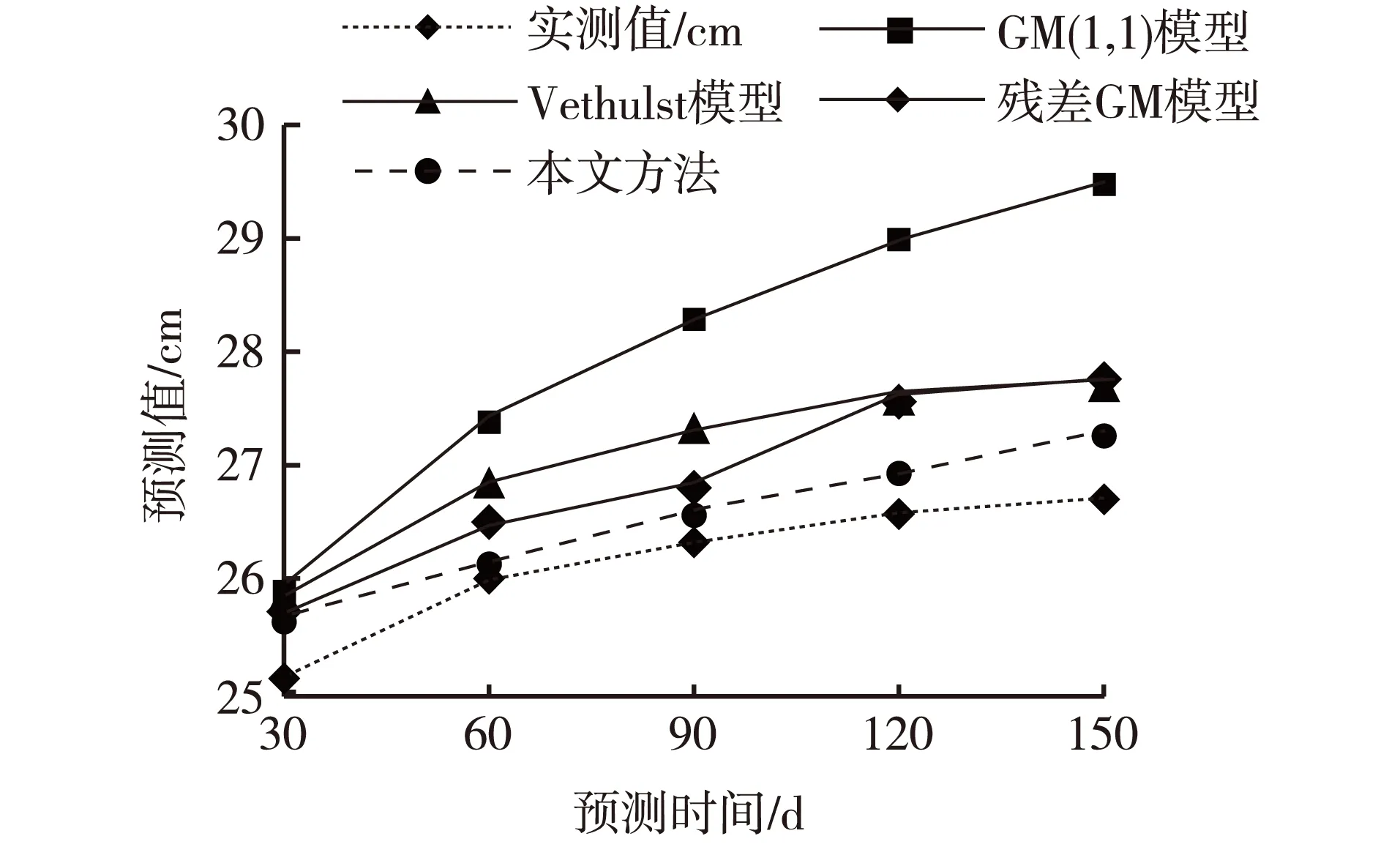
图1　沉降预测结果Fig. 1　Predicted settlement values obtained from different models

不断变动分数阶阶次β,使得式(18)结果最小,以确定最佳拟合效果,最终确定阶次β为0.232 7,对30 d、60 d、90 d、120 d、150 d预测结果分别为25.624 8 cm、26.130 0 cm、26.556 6 cm、26.929 0 cm、27.262 3 cm,比较结果如图1所示。

由图1可以看出,本文方法的预测值更精确。并进一步预测10 a后的沉降为37.50 cm,20 a后的沉降为41.04 cm,这符合通常堤坝、路基实际情况。

4　结　　语

整数阶微积分仅仅是分数阶微积分的特例,即所有含整数阶微积分的模型全部可以采用分数阶微积分代替,分数阶模型能够更好地反映实际情况。本文以灰色模型为对象,把其推广至分数阶模型,提出了分数阶阶次确定方法及调节因子的概念,从仿真结果来看,不仅具有灰色模型前期预测效果好的特点,而且具有灰色Verhulst模型后期预测效果好的特点,并且预测精度得到提高。此外,还具有长期预测结果稳定的特点。

但本文方法还存在一些缺陷:(a)计算过程复杂;(b)分数阶阶次和调节因子的确定需要不断观测仿真结果,比较麻烦。这2个缺陷也是笔者下一步需要解决的问题。

[1] 陈善雄, 王星运, 许锡昌,等. 路基沉降预测的三点修正指数曲线法[J]. 岩土力学,2011,32(11):3355-3361.(CHEN Shanxiong, WANG Xingyun, XU Xichang, et al. Three-point modified exponential curve method for predicting subgrade settlements[J]. Rock and Soil Mechanics,2011,32(11):3355-3361.(in Chinese))

[2] 秦植海, 秦鹏. 海堤地基固结系数反演与工后沉降分形模型预测[J]. 岩土力学,2012,33(6):1747-1754.(QIN Zhihai, QIN peng. Consolidation coefficient inversion of seawall foundation and prediction of its post construction settlement based on fractal theory[J]. Rock and Soil Mechanics,2012,33(6):1747-1754.(in Chinese))

[3] 王清, 桑伟锋, 徐黎明,等. 基于室内模拟实验的软土固结沉降的分形几何[J]. 吉林大学学报(地球科学版),2011,41(2): 465-470. (WANG Qing, SANG Weifeng, XU Liming, et al. Fractal geometry of consolidation settlement of soft soil based on simulation experiment[J]. Journal of Jilin University(Earth Science Edition), 2011, 41 (2): 465-470.(in Chinese))

[4] 冷伍明, 杨奇, 聂如松,等. 高速铁路桥梁桩基工后沉降组合预测研究[J]. 岩土力学, 2011, 32(11): 3341-3349.(LENG Wuming, YANG Qi, NIE Rusong, et al. Study of post-construction settlement combination forecast method of high-speed railway bridge pile foundation[J]. Rock and Soil Mechanics, 2011, 32(11): 3341-3349. (in Chinese))

[5] 刘寒冰, 向一鸣, 阮有兴. 背景值优化的多变量灰色模型在路基沉降预测中的应用[J]. 岩土力学, 2013, 34(1):173-182. (LIU Hanbing, XIANG Yiming, RUAN Youxing. A multivariable grey model based on background value optimization and its application to subgrade settlement prediction[J]. Rock and Soil Mechanics, 2013,34(1): 173-182. (in Chinese))

[6] 程健. 软土地基路堤工后沉降时参反演与预测[D]. 杭州,浙江大学, 2005.

[7] 高庆丰. 软土地基路堤工后沉降计算与预测[D]. 杭州,浙江大学,2003.

[8] 王高峰, 孙秀娟, 孙向东,等. 动态多变量灰色模型在危岩变形预测中的应用[J]. 河海大学学报(自然科学版),2014, 42(6):508-512.(WANG Gaofeng, SUN Xiujuan, SUN Xiangdong, et al. Application of dynamic multi-variable grey model to predication of deformation of unstable rock[J]. Journal of Hohai University(Natural Sciences),2014,42(6):508-512.(in Chinese))

[9] 肖佐城,王泽根.灰色模型在建筑沉降预测中的改进与发展[J].路基工程,2013(6):58-62.(XIAO Zuocheng, WANG Zegen. Improvement and development of gray model in settlement prediction for buildings[J]. Subgrade Engineering, 2013(6):58-62.(in Chinese))

[10] 王高峰,王洪德,薛星桥,等.巫山县望霞危岩体破坏及再次变形失稳预测分析[J].自然灾害学报,2012, 21(6): 164-172.(WANG Gaofeng, WANG Hongde, XUE Xingqiao, et al.Failure analysis of Wangxia dangerous rock mass in Wushan County and prediction its next deform and instability[J]. Journal of Natural Disasters, 2012,21(6): 164-172. (in Chinese))

[11] 沈毅, 郭金运, 周俊,等.基于灰色模型及其改进模型的土石坝沉降预测[J]. 山东理工大学学报(自然科学版),2014,28(1):6-9.(SHEN Yi, GUO Jinyun, ZHOU Jun,et al.Subsidence prediction of earth and rockfill dam based on gray model and its improved models[J]. Journal of Shandong University of Technology(Natural Science Edition), 2014,28(1):6-9.(in Chinese))

[12] 杨华龙, 刘金霞, 郑斌. 灰色预测GM(1,1)模型的改进及应用[J]. 数学的实践与认识, 2011,41(23):39-46.(YANG Hualong, LIU Jinxia, ZHENG Bin. Improvement and application of grey prediction GM(1,1) model[J]. Mathematics In Practice and Theory, 2011,41(23):39-46. (in Chinese))

[13] 程晨. 基于分数阶导数的软土流体力学性质研究[D]. 南京:河海大学,2012.

[14] 梁舒. 分数阶系统的控制理论研究[D]. 安徽:中国科学技术大学,2015.

[15] 秦文权. 客运专线复合地基上无碴轨道路基沉降的控制与计算分析研究[D]. 长沙:中南大学,2008.

Afractional-ordergreymodelforpredictionofsettlementofdykeswithfabricformsand

LIQian1,ZHOUXingde1,ZHOUZiyan2

(1. College of Civil and Transportation Engineering, Hohai University, Nanjing 210098, China;2. Wentian College, Hohai University, Maanshan 243031, China)

Inordertoacquirebetterforecastresultsforsettlementsofdykeswithfabricformsand,afractional-ordergreymodelispresentedbasedonthegreymodel.TheprogramwasestablishedusingMATLABtochangethedifferential-orderderivativeintoafractional-orderone.Thismodelwasusedtopredictthesettlementofdykeswithfabricformsand.ComparativeanalysisofthegreyVerhulstmodel,residualGMmodel,andproposedmodelwasperformed.Theresultsshowthatthepredictedresultsofthefractional-ordergreymodelaremoreaccurate,andthefractional-ordergreymodelnotonlyhasthereliablepreviousforecasteffectoftheGM(1, 1)model,butalsothereliablelaterforecasteffectoftheGreyVerhulstmodel.Moreover,thelong-termforecastresultsofthefractional-ordergreymodelshowahigherdegreeofstabilitythanthoseoftheGMmodel.

dykewithfabricformsand;settlementprediction;fractional-order;greymodel;greyVerhulstmodel;residualGMmodel

10.3876/j.issn.1000-1980.2016.05.010

2015-10-27

“十二五”国家科技支撑计划项目(2012BAB03B00);安徽省建设行业科学技术计划项目(2015YF-26)

李倩(1992—),女,江苏连云港人,硕士研究生,主要从事堤防稳定性及岩土工程数值分析研究。E-mail: 15195865755@163.com

周星德,教授。E-mail:xingdezhou@hhu.edu.cn

U213.1+57

A

1000-1980(2016)05-0438-05