基于改进PSO-LSSVM和蒙特卡洛法的电力系统可靠性评估

李孝全, 黄　超, 徐晨洋,王景辰

(空军工程大学防空反导学院,陕西 西安　710051)



基于改进PSO-LSSVM和蒙特卡洛法的电力系统可靠性评估

李孝全, 黄超, 徐晨洋,王景辰

(空军工程大学防空反导学院,陕西 西安710051)

针对电力系统可靠性评估方法耗时长、误差大等问题,提出一种用改进粒子群优化算法(PSO)优化最小二乘支持向量机(LSSVM)参数,并将构建好的PSO-LSSVM模型与蒙特卡洛法(MCS)相结合用于发输电系统可靠性评估的方法。该方法通过对PSO算法进行合理的改进,得到更为精确的LSSVM模型参数,建立用于分类系统状态样本的PSO-LSSVM模型。对MCS方法抽取的系统状态样本分类得到故障状态和正常状态,仅对故障状态样本进行可靠性指标计算,统计输出可靠性评估结果。采用该方法对IEEE-RTS 79系统不同运行情况下的可靠性指标进行计算,结果表明该方法保证计算时间不变的同时提高了LSSVM-MCS方法的评估精度。

电力系统;可靠性评估;粒子群算法;最小二支持向量机;蒙特卡洛法

当前电力系统评估的方法层出不穷,其中蒙特卡洛法(Monte Carlo simulation, MCS)是目前评估精度较高、且能适用于不同规模电力系统的方法。但该方法随着抽样状态的增多,评估状态的计算时间也随之剧增[1]。针对这一问题,对MCS的改进算法层出不穷,包括与模拟法混合使用的状态空间分割算法[2]、并行及分布算法[3]、降低方差系数[4]的改进MCS抽样技术算法,这些算法都在一定程度上解决了蒙特卡洛法收敛速度慢、评估耗时长的问题,但其都存在着模型计算结构复杂,评估误差较大的问题。近年来,人工神经网络的快速发展解决了多种问题的模式识别和预测问题,其与其他优化算法的结合使用效果更是优势突显。人工神经网络解决的电力系统问题主要集中在风力发电风速预测[5]、系统负荷预测[6-7]、设备故障诊断[8-9]等方面,解决电力系统可靠性评估的研究鲜见报道。王景辰等[10]提出了一种将最小二乘支持向量机(least squares support vector machine, LSSVM)与MCS方法相结合的电力系统可靠性评估方法;龚兰芳等[11]提出了一种将粒子群优化算法(particle swarm optimization, PSO)与支持向量回归法相结合的电力系统可靠性评估方法,这2种方法虽然大幅度缩短了电力系统可靠性评估的时间,但都存在着评估指标误差较大的缺点。

针对以上方法存在的问题,笔者提出一种应用PSO优化LSSVM模型参数,并将构建的PSO-LSSVM分类模型与MCS方法相结合的电力系统可靠性评估方法。通过PSO优化的LSSVM模型对MCS方法抽样出的系统状态分类精度更高,仅对分类出来的故障状态进行潮流计算,统计输出可靠性指标。PSO-LSSVM-MCS方法不仅继承了LSSVM-MCS方法评估时间短的优点,同时降低了可靠性评估的误差。最后，通过对IEEE-RTS 79系统的不同运行状态进行仿真计算,对本文方法的准确性及精度进行验证。

1　基于MCS的电力系统可靠性评估

蒙特卡洛法是一种最常用的评估电力系统可靠性的概率方法,其评估步骤如下:

a. 选择系统状态x=(x1,x2,…,xm),(m为系统元件个数),对系统中元件和负荷的状态进行随机抽样。

b. 对抽取的系统状态进行传统的潮流计算分析,通过计算结果判断系统状态是故障状态还是正常状态。

c. 采用步骤b获得的结果,更新系统可靠性参数。可靠性参数指标的期望值为

(1)

d. 当方差系数β(式(2))满足一定的精度要求时,停止计算,输出可靠性指标;反之,则返回步骤a。

(2)

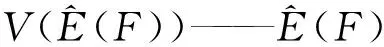
β的大小决定着计算所需的样本数量,两者的关系为

(3)

通过设置抽样的β值可以控制抽样的系统状态样本。

2　基于改进PSO算法优化LSSVM参数的原理

2.1LSSVM原理

LSSVM是标准支持向量机(support vector machine, SVM)的一种应用较为广泛的改进版本。具体原理可参考文献[5],模型原理概况如下:

a. 给定对应问题的训练样本。

b. 选择合适的核函数。需要选择一个适应能力强、结构简单、待确定和优化参数较少的核函数。本文选择径向基(RBF)函数(式(4))为LSSVM训练样本的核函数。

(4)

式中:xL和xK——训练样本;σ——径向基(RBF)函数特有参数。

c. 构造凸二次规划问题,建立拉格朗日函数解决优化问题。

d. 得到供训练样本的分类函数:

(5)

式中:yi——输出量;α*、b*——拉格朗日解决优化问题得到的最优解;l——训练样本的个数。

由于LSSVM采用径向基函数作为核函数训练样本，因此需要优化的参数共有2个——凸二次规划问题中的正规化参数γ和径向基函数中的参数σ。γ和σ的大小决定着LSSVM训练样本的误差大小，为不产生过训练或者欠训练的情况，达到预期的样本训练精度，必须采用合适的方法对这2个参数进行合适的优化。

2.2改进PSO算法

原始粒子群优化算法是一种基于群智能的随机优化算法，简单且易实现。在一个D维空间内，设第i(i=1,2,…，n)粒子的初始位置为pi=(pi1,pi2，…，pid)，d=1,2,…，D，飞行速度为si=(si1,si2，…，sid)，经历过最好的位置为qi=(qi1,qi2，…，qid)，能够获取群体的最好位置为qg=(qg1,qg2，…，qgd)，则参考文献[12]可得具体粒子群优化算法迭代计算公式：

(6)

(7)

式中:k——迭代次数;ω——惯性权重;r1、r2——加速因子,为非负常数;c1、c2——分布于[0,1]之间的随机数。

笔者提出一种改进的粒子群优化算法用以实现对γ和σ的优化选取，具体的改进包括两方面。

a. 在PSO算法的迭代过程中,ω设定过大虽然有利于提高整个算法的搜索能力,但同时剧增了算法的计算量与计算时间;ω设定过小有利于提高算法局部搜索能力,但容易使算法陷入局部最优的情况。为了更好地控制全局搜索与局部搜索的平衡,采用改进的惯性权重更新公式:

(8)

式中:kmax——最大迭代次数;ωk——第k次迭代的惯性权重;ωmax、ωmin——最大、最小惯性权重。

运用式(8)的二次型非线性递减算法确定ω,不仅提高了PSO的计算速度,并且保证了PSO参数寻优过程前期全局搜索能力和后期局部搜索确定最优值的能力。

b. 式(6)中的加速因子r1、r2的设定会影响到算法的收敛性问题,为了保证PSO算法绝对收敛、提高收敛速度,引入Clerc[10]收缩因子η到PSO的迭代公式中(式(6)),收缩因子计算公式为

(9)

其中

φ=r1+r2φ>4

改进后的PSO粒子位置和速度迭代寻优公式为

(10)

(11)

上述针对原始PSO算法的2个改进主要改进了原始PSO算法搜索精度较低、收敛速度慢等缺陷。

2.3利用改进的PSO算法优化LSSVM参数

利用改进PSO优化LSSVM参数的具体步骤:

a. 将所有待训练和待分类的样本数据归一化处理。

b. 初始化设置粒子群规模、ωmax、ωmin、kmax等参数。因为PSO算法只需优化参数γ和σ,所以空间维数D=2,在γ和σ的取值区间内随机初始化每个粒子的位置pi=(γiσi)与速度si=(ΔγiΔσi)。显然每个粒子的初始位置即为初始最好位置。

c. 粒子适应度值是评估粒子参数对应的LSSVM优劣的性能指标,把样本输出量的均方差作为适应度:

(12)

粒子位置越好,其适应度必然越小。对于单个粒子而言,将当前计算的适应度与历史最好位置的适应度作对比,如果当前适应度更小,则更新个体最优解为此粒子的位置,反之,则不更新;比较群体当前适应度与群体历史最好位置的适应度,如果群体当前适应度更小,则更新全局最优解为此群体的位置,反之,则不更新。

d. 应用改进的PSO粒子位置和速度迭代寻优式(10)(11),对粒子的位置和速度进行更新,产生新的种群。

e. 迭代终止条件有2个:是否达到最大迭代次数和适应度满足预设的精度要求。满足其中任何一个条件,即停止迭代,输出得到的最优化参数γbest和σbest,否则迭代次数加1,转到步骤c。

f. 输出改进PSO优化过的最优参数γbest和σbest,构建待训练LSSVM模型。

3　基于改进PSO-LSSVM和MCS的发输电系统可靠性评估

利用构建好的PSO-LSSVM模型结合MCS对发输电系统进行可靠性评估的具体步骤如下:

a. 建立LSSVM分类模型需要的系统状态样本数量较少,因此通过取定β可以控制MCS抽样评估的系统状态样本数,抽取的这一小部分系统状态通过潮流计算判断其类型(故障状态或正常状态),将这小部分系统状态作为构建LSSVM分类模型的训练集。

b. 由于步骤a中系统状态训练集是由MCS法抽样得到的,其中必然存在着大量重复状态,加大了后续LSSVM建模的计算负担,使用K-平均聚类算法对这部分系统状态训练集进行压缩,可以提高LSSVM的训练速度。

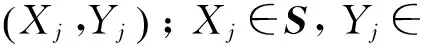
d. 由于电力系统状态分析中需要参考的变量很多,如可用发电容量、不可用发电容量、总发电容量、系统总负荷等,为了降低输入LSSVM模型变量的空间维数,选择系统可用发电容量和系统总负荷作为最相关的输入变量,用以训练和测试LSSVM分类模型。

e. 按照本文2.3节步骤用改进的PSO算法优化LSSVM模型得到最优化参数γbest和σbest,用基于γbest和σbest的LSSVM模型对步骤b得到的样本训练集S进行监督训练,采用k-折交叉确认[8](k-fold cross-validation) LSSVM评价分类精度,满足精度要求后,供发输电系统评估的PSO-LSSVM分类模型正式建立完毕。

f. 根据待评估的系统规模设置合适的β,采用MCS对系统状态进行抽样,需要注意的是这次抽样的系统状态只是单纯抽样,不经过潮流计算对其进行分析评估,利用步骤c构建好的PSO-LSSVM分类模型直接对其直接进行分类,得到故障状态和非故障状态。

g. 仅对故障状态进行可靠性指标计算,统计得到可靠性评估结果。

4　算 例 分 析

测试系统选用国际通用的IEEE-RTS 79[15],该系统包括发电机组32台,母线24条,支路38条,装机总容量3 405 MW,假设输电线路完全可用。将MCS和不经过粒子群优化参数的LSSVM-MCS方法及本文所提出的PSO-LSSVM-MCS方法应用到IEEE-RTS 79系统中,通过计算失负荷概率(loss of load probability, LOLP)和电量不足期望值(expected power not supplied, EPNS)来评价所提方法的可行性和有效性。

将负荷水平设置为2种情况:连续峰值负荷运行(算例1)和降低原始小时负荷运行(算例2)。使用上述3种方法计算系统在这2种负荷水平情况下的可靠性指标。仿真环境为Inter Core i3 3.4 Ghz处理器的主机,选用MATLAB 2013a中的LSSVMlab工具进行建模。

4.1系统连续峰值运行

将系统峰值负荷运行维持在2 800 MW,由于系统长时间运行在峰值状态,因此故障状态数目比正常水平要高,正常状态与故障状态比大约为2∶1。LSSVM-MCS方法的LSSVM分类模型建模过程得到的参数值:γ=0.111和σ2=4.307。本文PSO-LSSVM-MCS方法的PSO-LVVSM分类模型得到的参数值:γ=0.127和σ2=4.214。用上述3种方法经过10次仿真计算的指标平均值和绝对值误差平均值见表1。10次仿真计算LSSVM-MCS和PSO-LSSVM-MCS方法计算的可靠性指标LOLP和EPNS相对于MCS方法计算结果的误差如图1所示。

表1　算例1的 3种方法可靠性指标计算平均值对比Table 1　Comparison of average values of reliability index obtained from three kinds of methods for example 1

图1　算例1 LOLP、EPNS指标误差计算结果Fig. 1　Calculated results of LOLP and EPNS errors for example 1

由表1、图1可知,本文提出的PSO-LSSVM-MCS方法计算得到的可靠性指标较LSSVM-MCS方法误差更小,在LSSVM-MCS算法的基础之上,进一步提高了可靠性指标的计算精度,时间也较传统MCS方法缩短了4/5左右,与LSSVM-MCS方法所用时间大致相同。

4.2降低原始小时负荷运行

降低每个小时的平均负荷运行系统,由于负荷水平降低,正常状态数目与故障状态数目比例大约为8∶1。LSSVM-MCS方法的LSSVM分类模型建模过程得到的参数值[4]:γ=0.3047和σ2=8.6764。本文PSO-LSSVM-MCS方法的PSO-LVVSM分类模型得到的参数值:γ=0.2857和σ2=8.8623。再次用上述3种方法经过10次仿真计算的指标平均值和绝对值误差平均值见表2。10次仿真计算LSSVM-MCS和PSO-LSSVM-MCS两种方法计算的可靠性指标LOLP和EPNS相对于MCS方法计算结果的误差如图2所示。

表2　算例2的3种方法可靠性指标计算平均值对比Table 2　Comparison of average values of reliability index obtained from three kinds of methods for example 2

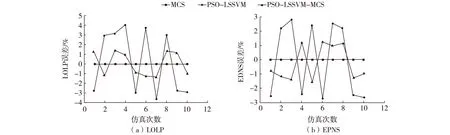
图2　算例2 LOLP、EPNS指标误差计算结果Fig. 2　Calculation results of LOLP and EPNS errors for example 2

由表2、图2可知,测试系统运行在较低负荷时,本文PSO-LSSVM-MCS方法计算得到的可靠性指标计算结果较LSSVM-MCS方法得到的结果误差更小,计算时间较传统MCS方法时间也有大幅度的缩短。

评估精度的提高得益于改进的PSO算法优化得到的参数较普通LSSVM训练样本数据得到的参数精度要高,计算时间的缩短得益于PSO-LSSVM模型通过对系统状态分类,避免了对正常状态的潮流计算过程。通过应用本文PSO-LSSVM-MCS方法对2个不同运行状态的系统实例进行可靠性评估可知,本文所提方法适用于不同运行状态的电力系统可靠性评估,具有一定的普适性。

5　结　　论

a. 通过对PSO算法适当改进,用改进PSO方法优化LSSVM分类模型的参数,以PSO优化得到的最优参数为基础构建用于分类系统状态的PSO-LSSVM分类模型,通过分类算例分析结果可知,本文的PSO-LSSVM-MCS方法较LSSVM-MCS方法的评估精度更高,得到的可靠性指标更为接近MCS方法的计算结果。

b. PSO-LSSVM-MCS方法的评估计算时间与LSSVM-MCS方法所用时间接近,改进PSO优化LSSVM参数过程在提高分类准确度的基础上并未以损失时间为代价,是可行的。

c. PSO-LSSVM-MCS继承了LSSVM-MCS方法的优点,可以避免正常状态的潮流分析过程,大幅度提升了MCS方法的评估速度。

[1] 赵渊, 周家启, 刘志宏. 大电网可靠性的序贯和非序贯蒙特卡洛仿真的收敛性分析及比较[J]. 电工技术学报,2009, 24(11): 127-133.(ZHAO Yuan, ZHOU Jiaqi, LIU Zhihong. Convergence analysis and comparison of sequential and nonsequential Monte-Carlo Simulation for bulk power system reliability assessment[J]. Transactions of China Electrotechnical Society, 2009, 24(11): 127-133.(in Chinese))

[2] 王晓滨, 黄武浩, 楼华辉,等. 系统状态空间分割法在电力系统可靠性评估中的应用[J]. 电网技术,2011, 35(10): 124-129.(WANG Xiaobin, HUANG Wuhao, LOU Huahui, et al. Application of state-space partitioning method in power system reliability assessment[J]. Power System Technology,2011, 35(10): 124-129. (in Chinese))

[3] 胡博, 谢开贵, 赵渊,等. 电力系统可靠性评估的动态任务分配并行算法[J]. 电力系统自动化,2011, 35(10): 35-41.(HU Bo, XIE Kaigui, ZHAO Yuan, et al. Parallel algorithm for reliability evaluation of bulk power system with dynamic task allocation technique[J]. Automation of Electric Power Systems, 2011, 35(10): 35-41. (in Chinese))

[4] 黄江宁, 郭瑞鹏, 赵舫，等. 电力系统可靠性评估中的分层均匀抽样法[J]. 电力系统自动化, 2012, 36(20): 19-24.(HUANG Jiangning, GUO Ruipeng, ZHAO Fang， et al. Stratified uniform sampling method for power system reliability evaluation[J]. Automation of Electric Power Systems, 2012, 36(20): 19-24. (in Chinese))

[5] 孙斌, 姚海涛. 基于PSO优化LSSVM的短期风速预测[J]. 电力系统保护与控制, 2012, 40(5): 85-89.(SUN Bin, YAO Haitao. The short-term wind speed forecast analysis based on the PSO-LSSVM predict model[J]. Power System Protection and Control,2012, 40(5): 85-89. (in Chinese))

[6] 余健明, 马小津, 倪峰,等. 基于改进PSO-LSSVM的风电场短期功率预测[J]. 西安理工大学学报,2013, 29(2): 176-181.(YU Jianming, MA Xiaojin, NI Feng, et al. Short-term power forecasting of wind farm based on an improved PSO-LSSVM[J]. Journal of Xi’an University Technology，2013, 29(2): 176-181. (in Chinese))

[7] 王贺, 胡志坚, 张翌晖,等. 基于 IPSO-LSSVM 的风电功率短期预测研究[J]. 电力系统保护与控制, 2012, 40(24): 107-112.(WANG He, HU Zhijian, ZHANG Yihui, et al. Short-term prediction of wind power based on IPSO-LSSVM[J]. Power System Protection and Control, 2012, 40(24): 107-112. (in Chinese))

[8] 贾嵘, 张云, 洪刚. 基于改进 PSO 的 LSSVM 参数优化在变压器故障诊断中的应用[J]. 电力系统保护与控制, 2010, 38(17): 121-124.(JIA Rong, ZHANG Yun, HONG Gang. Parameter optimization of least squares support vector machine based on improved particle swarm optimization in fault diagnosis of transformer[J]. Power System Protection and Control, 2010, 38(17): 121-124. (in Chinese))

[9] 朱克东, 郑建勇, 梅军,等. 基于LSSVM概率输出与证据理论融合的变压器故障诊断[J]. 河海大学学报(自然科学版), 2014, 42(5): 465-470.(ZHU Kedong, ZHENG Jianyong, MEI Jun， et al. Transformer fault diagnosis based on probability output of LSSVM and DS evidence theory[J].Journal of Hohai University (Natural Scineces), 2014, 42(5): 465-470. (in Chinese))

[10] 王景辰, 李孝全, 杨洋,等. 基于蒙特卡洛法和最小二乘支持向量机的复杂电力系统可靠性评估[J]. 华东电力,2013, 41(5): 1001-1004.(WANG Jingchen, LI Xiaoquan, YANG Yang, et al. Reliability evaluation of complex power system based on Monte Carlo simulation and least squares support vector machine[J]. East China Electric Power,2013, 41(5): 1001-1004. (in Chinese))

[11] 龚兰芳, 张昱. 电网可靠性评估的PSO-SVR评估模型[J]. 计算机仿真, 2011, 28(7): 196-199.(GONG Lanfang, ZHANG Yu. PSO-SVR evaluation model for power systems reliability evaluation[J]. Computer Simulation, 2011, 28(7): 196-199. (in Chinese))

[12] 仇军, 王景成. 基于PSO-LSSVM的城市时用水量预测[J]. 控制工程, 2014, 21(2): 232-236.(QIU Jun, WANG Jingcheng. Hourly urban water consumption prediction based on PSO-LSSVM[J]. Control Engineering of China, 2014, 21(2): 232-236. (in Chinese))

[13] 张春晓, 张涛. 基于最小二乘支持向量机和粒子群算法的两相流含油率软测量方法[J]. 中国电机工程学报, 2010, 30(2):86-90.(ZHANG Chunxiao, ZHANG Tao. Soft measurement method for oil holdup of two phase flow based on least squares support vector machine and particle swarm optimization[J]. Proceedings of the CSEE, 2010,30(2): 86-90. (in Chinese))

[14] 曹净, 丁文云, 赵党书,等. 基于 PSO-LSSVM 模型的基坑变形时间序列预测[J]. 控制工程, 2015,22(3): 475-480.(CAO Jing, DING Wenyun, ZHAO Dangshu, et al. Time series forecast of foundation pit deformation based on PSO-LSSVM[J]. Control Engineering of China, 2015,22(3): 475-480. (in Chinese))

[15] Reliability Test System Task Force. IEEE reliability test system[S]. New York:IEEE,1979.

Reliability evaluation of power system based on improved PSO-LSSVM and Monte Carlo simulation

LI Xiaoquan, HUANG Chao, XU Chenyang, WANG Jingchen

(CollegeofAirandMissileDefense,AirforceEngineeringUniversity,Xi’an710051,China)

The power system reliability evaluation methods are time-consuming and generate large errors. In order to solve these problems, a method for reliability evaluation of power systems is proposed based on the improved particle swarm optimization (PSO), the least squares support vector machine (LSSVM), and Monte Carlo simulation (MCS), where the improved PSO is used to optimize the parameters of SVM. The method can obtain more accurate LSSVM parameters through reasonable improvement of PSO, and a PSO-LSSVM model for classification of system state samples has been established. Using the PSO-LSSVM model to classify the system samples extracted by the MCS method, failure state samples and normal state samples were obtained with the PSO-LSSVM model. Reliability indices only for failure state samples were calculated and reliability evaluation results were output. This method was used to calculate the reliability index of the IEEE-RTS 79 system under different operation conditions, and the results show that the method improves the evaluation precision of the LSSVM-MCS method with a consistent amount of computation time.

power system; reliability evaluation; particle swarm optimization; least squares support vector machine; Monte Carlo simulation

10.3876/j.issn.1000-1980.2016.05.014

2015-12-14

李孝全(1968—)，男，安徽省淮南人，副教授，博士，主要从事电力系统可靠性、健康管理与故障诊断研究。 E-mail：379068078@qq.com

TM712

A

1000-1980(2016)05-0458-07