土石坝漫顶溃决模型的分析比较

陈淑婧,王秋生,于　沭,王洪洋

(1. 中国水利水电科学研究院岩土工程研究所,北京　100048; 2. 北京工业大学建筑工程学院,北京　100124)



土石坝漫顶溃决模型的分析比较

陈淑婧1,王秋生2,于沭1,王洪洋2

(1. 中国水利水电科学研究院岩土工程研究所,北京100048; 2. 北京工业大学建筑工程学院,北京100124)

为解决由现场溃坝过程记录资料匮乏导致的大量土石坝漫顶溃坝模型得不到工程验证的问题,在分析总结17种土石坝漫顶溃决机理模型基础上,以唐家山堰塞坝1/3溃坝事故为工程背景,选取BREACH模型、DB模型和IWHR模型对其溃坝过程进行数值模拟,研究这3种模型计算得到的筑坝材料冲蚀速率、流量过程线和水位变化曲线与实测值的差异。应用BREACH模型研究了筑坝材料的黏聚力、内摩擦角、不均匀系数和孔隙率对流量过程线的影响。结果表明:(a)IWHR模型预测的洪峰流量最大,BREACH模型次之,DB模型最小;(b)与实测数据相比,DB模型和IWHR模型预测的峰现时间提前,BREACH模型预测的峰现时间推迟;(c)随着黏聚力和内摩擦角的增大,计算峰值流量减小,峰现时间延后;(d)随着孔隙率和不均匀系数的增大,计算峰值流量增大,峰现时间提前;(e)不均匀系数和孔隙率对溃坝计算结果的敏感性尤为显著。

土石坝;漫顶溃坝模型;参数敏感性分析;冲蚀速率;流量过程线;水位变化曲线;唐家山堰塞坝

土石坝是国内外应用最广泛的坝型,约占已建坝总数的95%以上[1]。土石坝的溃坝机理和风险调控研究历来受到坝工界的普遍重视。由于溃坝过程、溃坝机理和影响因素等比较复杂,因此目前土石坝溃坝问题仍然是一个研究的热点和难点。

当前的土石坝溃坝计算模型分为参数模型和机理模型2类。参数模型[2-3]通过对大量溃坝数据进行多变量回归分析而得到,其准确性依赖于溃坝过程的实时记录,但溃坝属于灾难性事故,对溃坝过程的详细记录较少,许多数据要通过浸润线位置和最终溃口尺寸反演得到。机理模型[4-6]通过综合分析库容变化、溃口侧壁坍塌和洪水对溃口的冲蚀三方面,计算溃坝的流量过程线和库水位下降曲线,尤其考虑了水土介质的相互作用,理论上更加完善。尽管近年来发展了大量的土石坝溃坝机理模型,但由于溃坝实测资料匮乏,这些模型大都没有得到很好的工程验证。同时坝体材料参数对溃坝过程有重要影响,模型参数的敏感性分析也缺少系统的研究。

基于对当前常用土石坝溃坝机理模型的分析总结,以唐家山堰塞坝1/3溃坝为工程背景,选取3个典型机理模型对其溃坝过程进行数值模拟,研究坝体材料冲蚀速率、溃坝流量过程线和库区水位变化曲线与实测值的差异,并应用BREACH模型研究筑坝材料的黏聚力、内摩擦角、孔隙率和不均匀系数对流量过程线的影响。

1　土石坝漫顶溃坝机理模型

土石坝漫顶溃坝机理模型分为流量平衡方程、坝体材料抗冲临界剪应力和冲蚀速率计算、溃口侧壁扩展计算3个部分。

1.1流量平衡方程

土石坝溃坝过程中,入库流量、库容单位时间的变化量和出库流量相等:

(1)

式中:I——入库流量;O——出库流量,一般使用宽顶堰公式计算,包括泄洪道流量、坝顶溢流和溃口流量;W——库容。

1.2坝体材料抗冲临界剪应力和冲蚀速率

1.2.1临界剪应力

水力冲蚀是土石坝漫顶溃坝的诱因和主导因素。水流运动对坝体顶面土颗粒施加拖拽剪应力,当该剪应力超过临界剪应力时,土颗粒开始移动,坝体被冲蚀,与临界剪应力对应的水流平均速度称为土颗粒的抗冲流速。抗冲流速一定程度上决定了土石坝冲蚀的起始时间和终止时间。Chen等[7]研究表明,坝体材料抗冲流速和冲蚀速率是影响机理模型预测结果的主要因素。

Shields[8]通过大量的水槽试验,研究了无黏性土的抗冲蚀特性,并绘制了Shields曲线;Briaud等[9]应用冲蚀函数测定仪进行了大量试验研究,发现临界剪应力和平均粒径之间存在良好的对应关系,与Shields[8]的试验结果相似;但是对于黏性土,双电子层的存在增强了土体的抗冲蚀性能,临界剪应力和土颗粒平均粒径之间不存在唯一的对应关系。在溃坝计算中还常用Schoklitsch公式和Meyer-Peter & Muller公式[4]计算土体的临界剪应力。

1.2.2冲蚀速率

冲蚀速率与土性参数、临界剪应力、水流参数等物理量有关。由于土体性质的不确定性,黏性土、无黏性土和不同压实状态土体的冲蚀速率和水流速度(剪应力)的关系曲线有很大差别。Briaud等[9]指出,大部分土体的冲蚀速率和剪应力的关系曲线呈凹线型,但也有呈直线型或凸线型的。当前土体冲蚀计算广泛沿用泥沙动力学中的推移质计算理论,如Meyer-Peter & Muller公式[4]、Eintein-Brown公式[5]、DuBoy公式[10]、Engelund-Hansen公式[11]、Schoklitsch公式[12]等。另外,在溃坝计算研究中,各国学者根据现场实测和室内试验资料相继提出了土石坝溃坝冲蚀计算公式,如直线型、指数型和双曲线型公式。值得提及的是,虽然当前指数型冲蚀速率公式应用最为广泛,但是冲蚀速率关于参数有极强的敏感性,比如Chen等[7]在唐家山堰塞坝的溃坝模拟中,冲蚀参数从1.25变为1.3,洪峰流量从7 513 m3/s变为15 192 m3/s。

1.3溃口扩展模式

在已有的土石坝溃坝模型中,常把溃口简化为矩形、梯形、抛物线形或圆弧形。如BRDAM模型[10]中假设溃口形状为抛物线形,溃口侧壁坡度为45°,顶面宽度为溃口深度的3.75倍;BREACH模型[4]假设溃口初始形状为矩形,当坝体冲蚀达到一定深度时溃口侧壁坍塌,形成梯形溃口;BEED模型[5]通过底宽、高度和坡度定义溃口形状,采用考虑渗透力及扬压力的简化边坡稳定分析理论验算溃口边坡的稳定性;Chen等[7]采用极限平衡理论计算溃口稳定性,溃口形状为圆弧形。

对于溃口的稳定性计算,数值模型中多采用滑坡计算原理,但从现场和试验过程可以发现:溃口侧壁坍塌表现出明显的三维特征,即坝体漫顶后,下游坡首先被冲蚀,期间伴随着侧壁坍塌,这种坍塌往往是局部小范围的,不存在横贯土石坝的滑坡体,随着水流下切,逐渐有大型的滑坡体产生,另外溃口侧壁一般都很陡,近于直立,坍塌机理有别于一般的滑坡问题。

1.4当前较常用的土石坝溃坝机理模型

为了便于比较土石坝漫顶溃决模型的计算原理,表1按文章发表的时间顺序,从溃口形状、冲蚀速率计算公式和流量计算公式三部分总结了当前较常用的17种机理模型,总结了模型的发展过程。其中,BREACH模型[4]采用修正的Meyer-Peter & Muller公式计算溃口冲蚀速率,考虑了溃口上游周边和侧壁的坍塌对溃口冲蚀速率的影响,是现今应用最为广泛的溃口发展模型;DB模型[11]采用Engelund-Hansen公式计算冲蚀速率,可输入冲蚀计算的终止条件,是较为完善的商业模型;IWHR模型[7]提出并使用双曲线型冲蚀速率公式,采用极限平衡理论计算溃口侧壁坍塌,提出了一种无须迭代的新型溃坝模型。下文将此3种模型应用到工程实例中,探讨其计算准确性和稳定性。

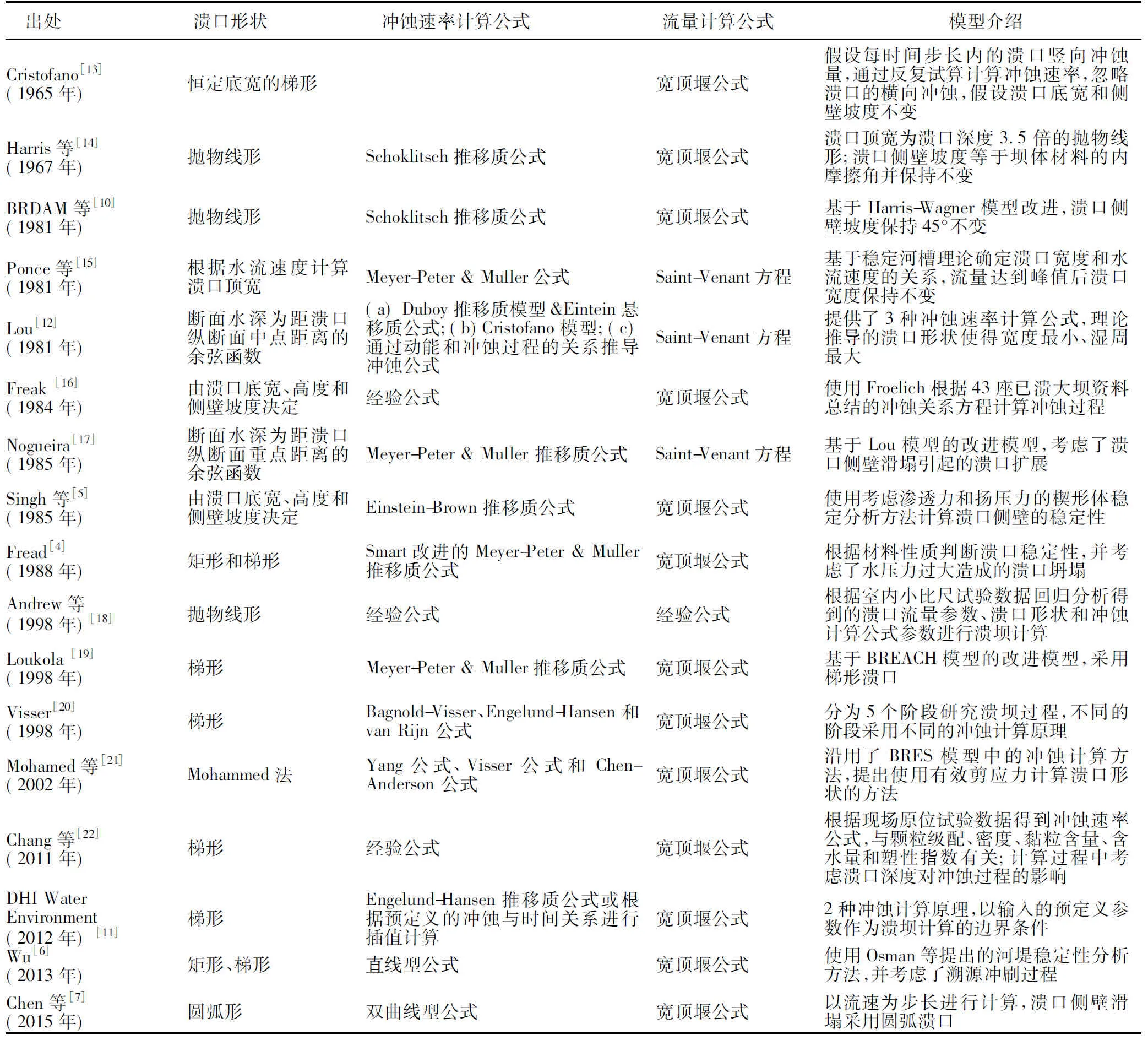
表1　17种漫顶溃坝机理模型总结Table 1　Summary of 17 models for analysis of mechanisms of overtopping-induced dam breach

2　唐家山堰塞坝概况

唐家山堰塞坝是汶川地震中形成的规模最大、危害最严重的堰塞坝,坝顶高程为752 m,沿河坝长803 m,横河坝长603 m,库容为3.2 亿m3。堰塞坝处理过程中,开挖了一条总长475 m,上游段深12 m、下游段深13 m的泄流槽。泄流槽开挖后,进口高程降低为741 m,库容降为2.3 亿m3,上游坡较缓,坡度约20°(坡比约1∶4),下游坝坡分3段,上部陡坡长约50 m(坡度约55°),中部缓坡长约230 m(坡度约32°),下部陡坡长约20 m(坡度约64°),平均坡比为1∶2.4[23]。堰塞体为宽级配土,从坝体上表面到坝底依次为黄褐色坡残积碎石土,强风化岩体破碎后的块碎砾石层和弱风化岩体解体后的似层状碎裂岩体,平均粒径5～17 mm[24]。Chen等[7]详细地列出了溃坝过程的实测数据,包括流量、水深、水流流速、溃口宽度等,不可直接测量的水流剪应力则通过明渠均匀流公式计算得到。

3　唐家山堰塞坝溃决过程模拟

图1　冲刷率实测值和计算值对比Fig. 1　Comparisons of calculated and measured results of erosion rate

结合唐家山堰塞坝的溃坝实测资料,使用3种溃坝模型(BREACH模型、DB模型以及IWHR模型)模拟其溃坝过程。图1是3种溃坝模型计算的坝体冲蚀速率与实测值对比。由图1可知,使用Engelund-Hansen公式计算冲蚀速率的DB模型比实测值小;在实测冲蚀速率较低时,IWHR模型使用的双曲线型冲蚀速率公式计算的结果偏大,在实测冲蚀速率较高时,BREACH模型使用的改进Meyer-Peter & Muller公式的计算结果偏大。实测资料显示冲蚀速率的平均值约为0.5 mm/s,3种公式中,双曲线型冲蚀速率公式的计算值最大(为0.84 mm/s),修正的Meyer-Peter & Muller公式计算结果为0.70 mm/s,Engelund-Hansen公式的计算值仅为0.27 mm/s。

唐家山堰塞坝的实测溃坝资料显示[7],溃决从2008年6月10日6:00开始,到当日12:30溃口流量达到最大值(6 500 m3/s),坝体冲刷高度约30 m,水库水位降为715 m。图2给出了流量过程线和库水位曲线的计算结果,DB模型和IWHR模型计算得到的洪峰到达时间分别为10:09和10:51,比实测洪峰到达时间提前。BREACH模型的计算结果为14:30,比实测洪峰到达时间延后。造成该结果的影响因素复杂,其中一个重要的原因是DB模型和IWHR模型没有考虑溃口侧壁坍塌土体对溃口冲蚀过程的影响,计算得到的溃口扩展速度比实际情况偏大;而BREACH模型考虑了溃口侧壁坍塌土体对溃口冲蚀的影响,但是假设坍塌土体和未坍塌前该部分土体的物理力学性质一致,计算得到的溃口扩展速度比实际情况偏小。IWHR模型、BREACH模型和DB模型的计算洪峰流量分别为7 470 m3/s、6 195 m3/s和4 795 m3/s,该结果的大小顺序与上述3个模型计算的平均冲蚀速率大小顺序吻合。

图2(b)给出了库水位变化曲线,结果显示DB模型的模拟结果比其他2种模型准确。实际情况中,在715 m下由于大块石基岩的存在,溃坝冲蚀过程基本停止。DB模型计算过程中需输入最终溃口的高程,当溃口下切到预定义高程时,程序停止计算,所以模型的计算趋势和实测数据较吻合,而BREACH模型和IWHR模型从坝体材料性质出发,计算得到的库水位曲线与实测数据差别较大。

4　模型参数敏感性分析

从冲蚀速率计算、流量过程线计算结果可以看出,BREACH模型在溃坝计算中适用性较强,并且模型中充分考虑了材料性质,为了定量探究材料参数对流量过程线的影响,以BREACH模型对唐家山堰塞坝的溃坝模拟为基础,保持其他参数不变,分别变换黏聚力、内摩擦角、不均匀系数和孔隙率4个基本材料参数的取值,观察流量过程线的变化,结果如图3所示。

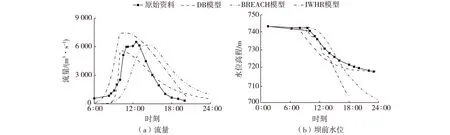
图2　流量、坝前水位模拟结果和实测数据对比Fig. 2　Comparison of calculated and measured results of discharge and water level in front of dam

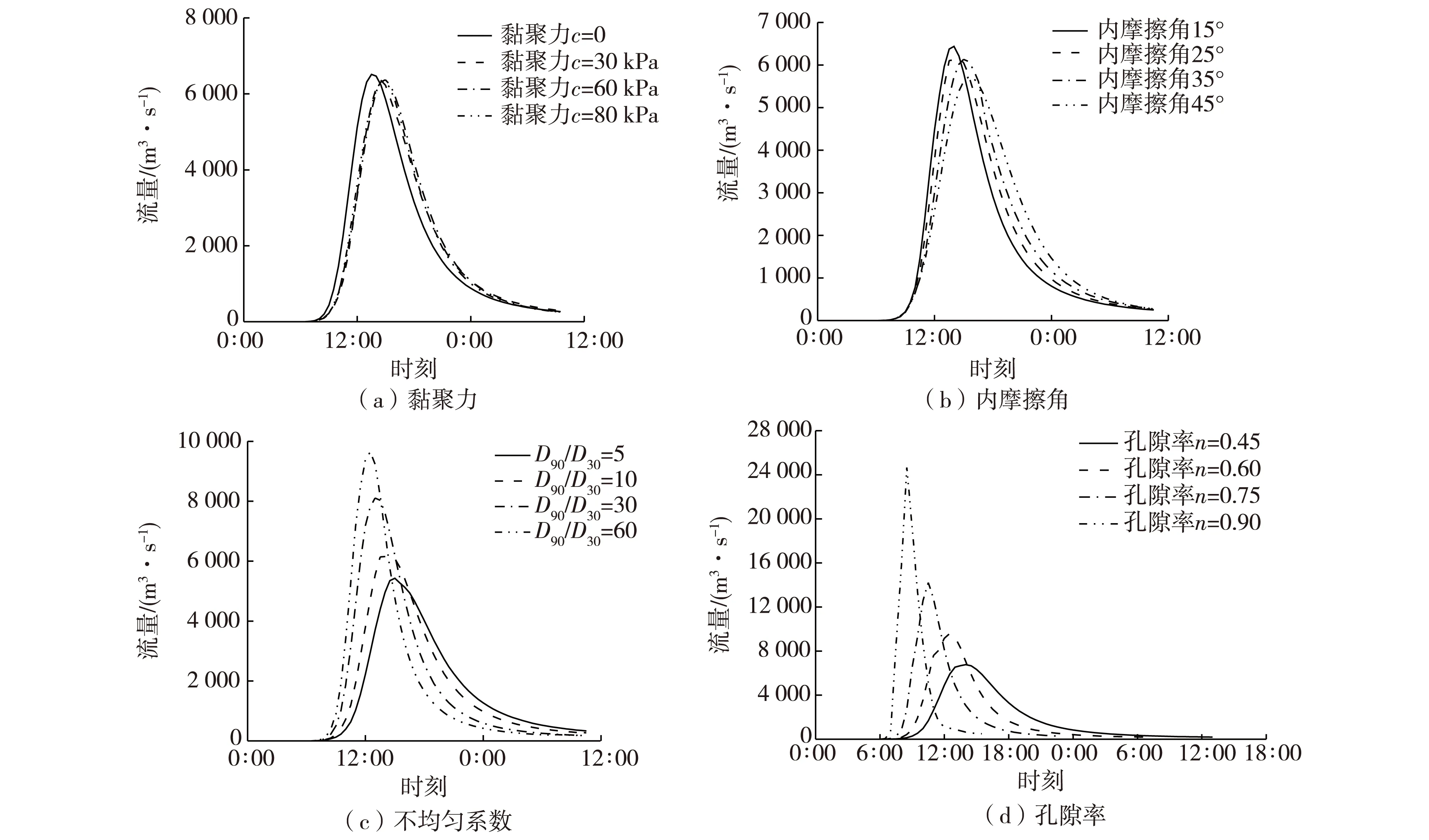
图3　2008年6月10—11日参数敏感性分析结果Fig. 3　Results of parameter sensitivity analysis for period from June 10 to June 11, 2008

从图3可以看出,4个参数对流量过程线影响的基本规律是一致的,随着黏聚力和内摩擦角的增大,计算峰值流量降低,峰现时间明显延后;随着孔隙率和不均匀系数的增大,计算峰值流量变大,峰现时间提前。与直观意识相同,随着黏聚力和内摩擦角增大,土体强度增强,其抗冲刷能力强,溃坝过程延缓;孔隙率的增大,导致土体内部结构松散,强度降低,溃坝过程加速。但模拟结果显示随着不均匀系数的增大会加快溃坝过程,结合实际情况分析,土石坝或堰塞坝由大量大颗粒组成,且经过充分压实,压实作用导致大颗粒之间咬合力增强,土体材料组成越单一,抗冲刷性越强,渗透稳定性高,可以延缓溃坝过程。

由图3可知,不均匀系数和孔隙率对模型预测结果的影响远大于黏聚力和内摩擦角。其直接原因是抗冲流速和冲蚀速率公式大都表示为诸如土颗粒平均粒径、颗粒级配特征等物理参数的函数,而抗冲流速(临界剪应力)和冲蚀速率是影响土石坝溃坝机理模型预测结果的主要因素,因此在土石坝溃坝模拟时,当所用模型的抗冲流速和冲蚀速率公式表示为土的物理参数的函数时,应特别注意物理参数的准确量测和输入。

5　结　　论

a. IWHR模型预测的洪峰流量最大,BREACH模型次之,DB模型最小;与实测数据相比,DB模型和IWHR模型预测的峰现时间提前,BREACH模型预测的峰现时间推迟。

b. 溃坝计算中,随着黏聚力和内摩擦角的增大,计算峰值流量降低,峰现时间明显延后;随着孔隙率和不均匀系数的增大,计算峰值流量变大,峰现时间提前。

c. 筑坝材料抗冲流速和冲蚀速率是影响机理模型预测结果的主要因素,且它们往往表示为土的物理参数的函数,而通过敏感性计算可以发现不均匀系数和孔隙率对计算结果的影响尤为显著,为溃坝计算中参数的选取提供了参考依据。

[1] 牛运光. 水库土石坝防洪标准综述[J]. 人民珠江,1999(1):34-39. (NIU Yunguang. A review of reservoir flood control embankment dam standard [J]. People of the Pearl River, 1999(1):34-39. (in Chinese))

[2] FROEHLICH D. Embankment dam breach parameters revisited[J]].Water Resources Engineering, 1995,1: 887-891.

[3] MACDONALD T C, LANGRIDGE-MONOPOLIS J. Breaching characteristics of dam failures[J].Journal of Hydraulic Engineering, 1984, 110(5): 567-586.

[4] FREAD D L. BREACH: an erosion model for earthen dam failures [M]. Washington D C: National Weather Service, NOAA, 1988.

[5] SINGH V P, SCARLATOS P D, COLLINS J G. Breach erosion of earthfill dams (BEED) model[J]. Natural Hazards,1988,1(2):161-180.

[6] WU Weiming. Simplified physically based model of earthen embankment breaching[J]. Journal of Hydraulic Engineering, 2013,139(8): 837-851.

[7] CHEN Zuyu, MA Liqiu, YU Shu, et al. Back analysis of the draining process of the Tangjiashan barrier lake [J]. Journal of Hydraulic Engineering, 2015,141(4): 05014011.

[8] SHIELDS A. Application of similarity principles and turbulence research to bed-load movement[R]. Pasadena: California Institute of Technology,1936.

[9] BRIAUD J L, TING F C K, CHEN H C, et al. Erosion function apparatus for scour rate predictions[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001,127(2):105-113.

[10] BROWN R J, ROGERS D C. BRDAM users’ manual[M]. Denver: US Department of the Interior, Water and Power Resources Service, 1981.

[11] DHI Water Environment．A modeling system for rivers and channels user guide[R]. California: MIKE Documentation, DHI Group,2012.

[12] LOU W C. Mathematical modeling of earth dam breaches [D]. Fort Collins: Colorado State University, CO, 1981.

[13] CRISTOFANO E A. Method of computing erosion rate for failure of earthfill dams[M]. Denver:US Department of the Interior, Bureau of Reclamation, Engineering and Research Center, 1973.

[14] HARRIS G W, WAGNER D A. Outflow from breached earth dams[D].Salt Lake City:University of Utah, 1967.

[15] PONCE V M, TSIVOGLOU A J. Modeling gradual dam breaches[J].Journal of the Hydraulics Division, 1981, 107 (HY7), 829-838.

[16] FREAK D L. DAMBRK: the NWS dam break flood forecasting model[M]. Washington D C: Hydrologic Research Laboratory, National Weather Service, NOAA, 1984.

[17] NOGUEIRA V P Q. Mathematical model of progressive earth dam failure [D]. Fort Collins: Colorado State University, 1985.

[18] COLEMAN S E, ANDREWS D P, WEBBY M G. Overtopping breaching of noncohesive homogeneous embankments[J]. Journal of Hydraulic Engineering, 2002, 128(9): 829-838.

[19] LOUKOLA E, HUOKUNA M. A numerical erosion model for embankment dams failure and its use for risk assessment [R]. Munich: Lockeed Company, 1998.

[20] VISSER P J. Breach growth in sand-dikes[M]. TU Delft: Delft University of Technology, 1998.

[21] MOHAMED M A, SAMUELS P G. MORRIS M W, et al. Improving the accuracy of prediction of breach formation through embankment dams and flood embankments [R] . Wallingford :HR Wallingford, 2002.

[22] CHANG D S, ZHANG L M, XU Y, et al. Field testing of erodibility of two landslide dams triggered by the 12 May Wenchuan earthquake[J]. Landslides, 2011,8(3): 321-332.

[23] LIU Ning, CHEN Zuyu, ZHANG Jianxin, et al. Draining the Tangjiashan barrier lake[J]. Journal of Hydraulic Engineering, 2010,136(11):914-923.

Comparative analysis of models for overtopping-induced earth-rock dam breach

CHEN Shujing1, WANG Qiusheng2, YU Shu1,WANG Hongyang2

(1.DepartmentofGeotechnicalEngineering,ChinaInstituteofWaterResourcesHydropowerResearch,Beijing100048,China;2.CollegeofArchitectureandCivilEngineering,BeijingUniversityofTechnology,Beijing100124,China)

Due to the lack of detailed field data recording the dam breach process, most of the models for overtopping-induced dam breach analysis of earth-rock dams have not been fully validated. In view of this problem, 17 models for analysis of mechanisms of earth-rock dam breach are summarized. The BREACH model, DB model, and IWHR model were used to simulate 1/3 of the accidents involving the Tangjiashan barrier dam breach, and the differences between measured and calculated results regarding the erosion rate of dam materials, discharge curve, and water level curve were analyzed. The influences of cohesion, the internal frictional angle, the non-uniformity coefficient, and porosity of dam materials on the discharge curve were studied with the BREACH model. The results show that the peak discharge predicted by the IWHR model is the highest, followed by those predicted by the BREACH model and DB model; the time, corresponding to the peak discharge, obtained by the DB model and IWHR model, is earlier than that obtained by measurement, while the corresponding time obtained by the BREACH model is later than that obtained by measurement; with the increase of cohesion and the internal frictional angle, the calculated peak discharge decreases and the corresponding time is delayed; with the increase of porosity and the non-uniformity coefficient, the peak discharge increases and the corresponding time comes earlier; and the non-uniformity coefficient and porosity have a significant influence on the calculated results regarding the dam breach.

earth-rock dam; model for overtopping-induced dam breach; parameter sensitivity analysis; erosion rate; discharge curve; water level curve; Tangjiashan barrier dam

10.3876/j.issn.1000-1980.2016.05.005

2015-09-21

国家重点基础研究发展计划(973计划)(2013CB036402);国家自然科学基金青年基金(51309260)

陈淑婧(1991—),女,山东潍坊,博士研究生,主要从事土石坝溃坝机理和风险控制研究。E-mail:1023751816@qq.com

TV641

A

1000-1980(2016)05-0406-06