滑移对部分充填式钢箱-砼组合梁承载力的影响
班志鹏, 江雪, 郑艳, 胥海宁
(1. 桂林理工大学 广西岩土力学与工程重点实验室, 广西 桂林 541004 2. 桂林理工大学 土木与建筑工程学院, 广西 桂林 541004)

滑移对部分充填式钢箱-砼组合梁承载力的影响
班志鹏1,2, 江雪1, 郑艳1, 胥海宁1
(1. 桂林理工大学 广西岩土力学与工程重点实验室, 广西 桂林 541004 2. 桂林理工大学 土木与建筑工程学院, 广西 桂林 541004)
为了分析滑移对受负弯矩作用的部分充填式钢箱-混凝土组合梁弹性抗弯承载力的影响,建立在反向两点对称加载工况下的组合梁微段模型,并推导滑移微分方程,在此基础上得出滑移和滑移应变解析解.根据截面应变分布,进一步推导出组合梁考虑滑移效应的弹性抗弯承载力计算公式.对3根反向两点对称加载的组合梁进行试验,对公式的准确性进行验证,试验得出的结果与公式计算值之间拟合良好.结果表明:考虑滑移的不利影响后,组合梁的弹性抗弯承载力下降明显.
部分充填式钢箱-混凝土组合梁; 负弯矩区; 滑移; 弹性抗弯承载力
传统的钢-混凝土组合梁在钢梁部分采用工字型钢,在受正弯矩作用时能充分地发挥材料强度,但在受负弯矩作用时容易发生失稳.针对这一问题,钟新谷等[1]提出了钢箱-混凝土组合梁新式截面,这一形式的组合梁在负弯矩区有明显的受力性能优势.文献[2-4]相继对内填混凝土的钢箱梁进行了研究,并取得了一定成果.在此基础上,羊海林等[5-6]提出了部分充填式钢箱-混凝土连续组合梁的结构形式,这类连续组合梁负弯矩区的设计尤为关键,对其进行深入的研究十分必要.组合梁由于界面连接采用栓钉这类的柔性抗剪连接件,在荷载作用下,混凝土和钢梁的交接面用于连接件的变形,不可避免地出现滑移.大量研究表明,组合梁的抗弯承载力受到滑移效应的影响,使组合梁的弹性抗弯承载力达不到按截面换算法计算的承载力值,这点在设计上尤为重要.目前,国内外学者对于滑移效应的研究主要集中于正弯矩区[7-10]、而对负弯矩的滑移效应研究相对较少.本文在反向对称集中荷载作用下,对3根不同配筋率的部分填充式钢箱-混凝土简支组合梁进行了试验,并在负弯矩作用下,尝试推导部分充填式钢箱-混凝土简支组合梁的计算公式.通过对比分析试验结果与计算结果,证明公式的准确性.
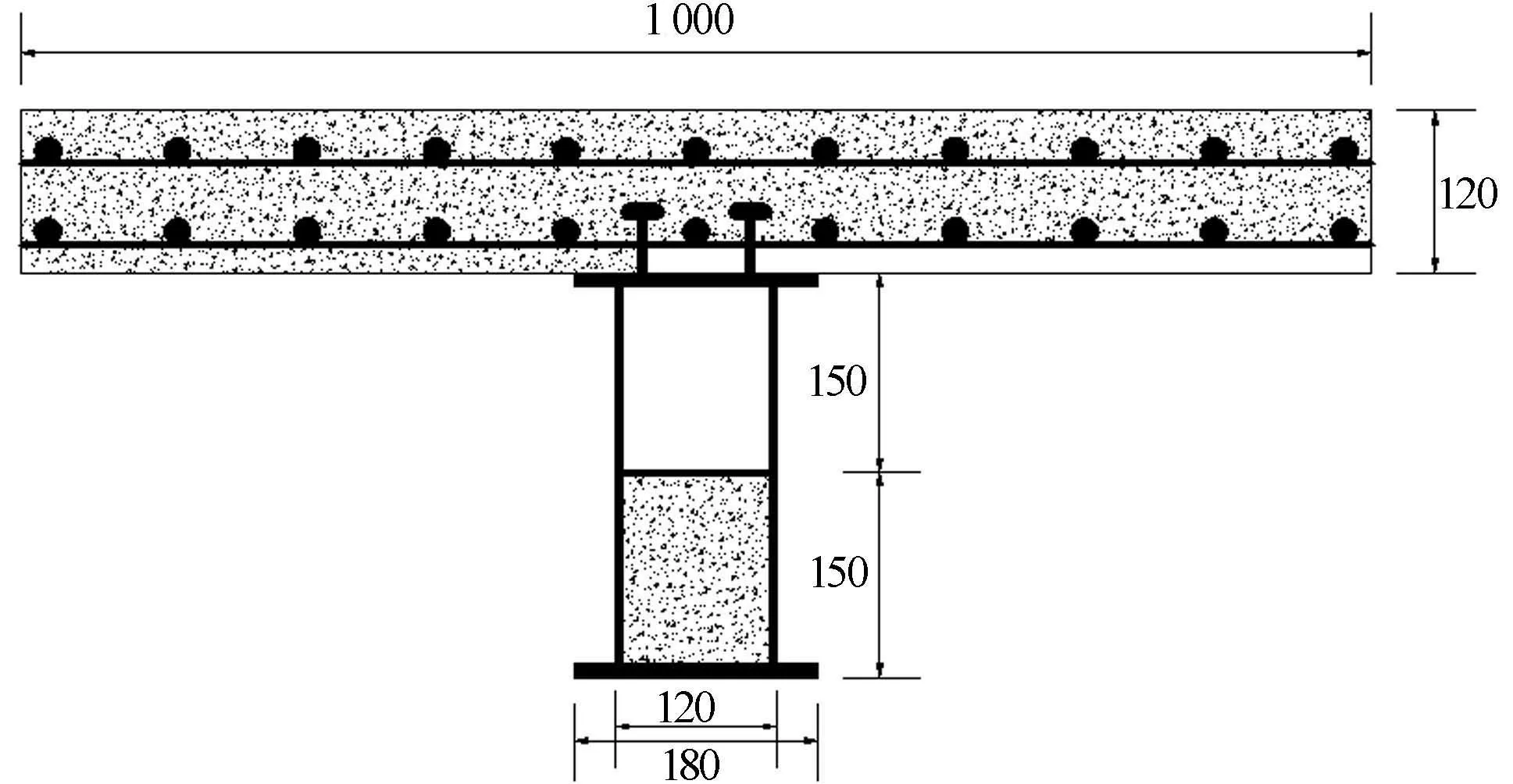
图1 组合梁横截面(单位: mm)Fig.1 Section of composite beam(unit: mm)
1 试验概况
1.1试件设计
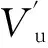

表1 试件参数

表2 钢材的力学性能Tab.2 Performanceofsteel材料名称fy/MPafst/MPaE/MPa纵向钢筋4356060.200横向钢筋3154710.200钢箱梁2854050.206表3 推出试件的试验结果Tab.3 Resultofpushouttest推出试件编号V'u/kNVu/kN215376722580722359073
1.2加载方案与测量方案
为了模拟连续组合梁负弯矩区的受力状态,尝试对简支组合梁进行反向加载.试验通过油压千斤顶施加荷载,并在油压千斤顶上放置压力传感器,用于读出每级所施加荷载的大小.在千斤顶和组合梁之间还放置了分配梁,将千斤顶提供的集中力转化为一对反向的对称集中荷载,传递给组合梁,两点集中荷载的间距为1 400 mm.梁两端的支座利用反力架固定.试验装置和加载设备,如图2所示.试验的测量内容包括滑移、挠度和应变.滑移和挠度通过百分表测量,由人工读出;应变通过应变片和应变采集仪进行测量.
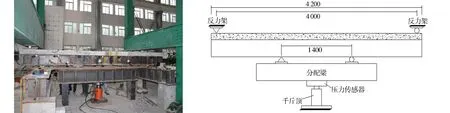
(a) 实景图 (b) 设计图 图2 试验装置和加载设备(单位: mm)Fig.2 Test device and loading equipment(unit: mm)
1.3试验结果
根据试验结果,3个试件的钢筋和钢箱底板荷载-应变关系曲线,如图3所示.由图3可知:3个试件的钢筋应变曲线在加载到100 kN附近时,出现了第一个转折点,表示混凝土面板已经开裂,钢筋承受的荷载继续增加,进而钢筋拉应变发生突增;在钢箱底板应变曲线中,试件PSCB2-1和PSCB2-5分别在250,400 kN附近出现折点,可能是由于加载到该级荷载时,钢箱梁和混凝土翼板的交界面发生较大滑移,导致钢箱底板的压应变增大;继续加载直到钢箱底板或钢筋达到屈服应变时,认为组合梁截面已经达到了弹性承载力的极限状态,钢箱底板所用钢材的屈服应变在1 400×10-6左右,而钢筋的屈服应变在2 200×10-6左右,钢箱底板先于钢筋屈服.

(a) 钢筋 (b) 钢箱底板图3 跨中截面荷载-应变曲线Fig.3 Curves of load-strain of cross section
2 负弯矩作用下组合梁的滑移分析
2.1基本假定
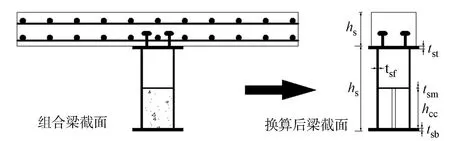
图4 组合梁换算截面Fig.4 Section of composite beam conversion
引入如下4个假定对部分填充钢箱-混凝土梁进行弹性分析.1) 平截面假定.2) 同一截面的钢箱与混凝土面板具有相同的变形曲率.3) 钢材与混凝土均为服从胡克定律的线弹性材料.4) 混凝土与钢箱交界面上的纵向剪力与相对滑移成正比例关系.
2.2截面换算
部分填充钢箱-混凝土梁材料组成并不单一,在计算其弹性阶段的截面特性时,需将截面换算为同种材料,如图4所示.文中用等效的钢截面替代全部混凝土截面,并使换算前后混凝土截面的高度保持不变,仅改变其宽度,从而使换算前后填充混凝土和混凝土面板形心位置不变.
按截面换算法计算的换算后钢截面面积为
(1)
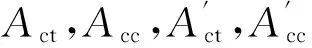
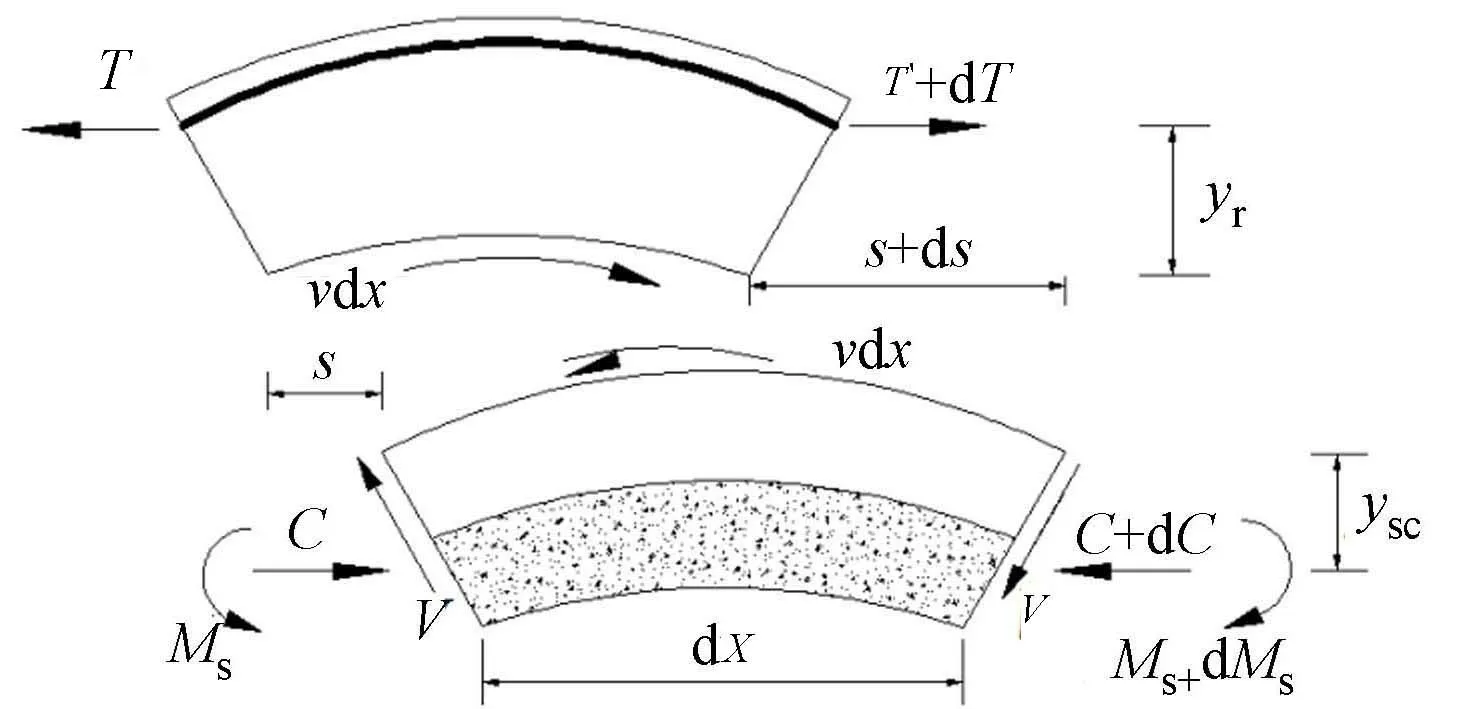
图5 组合梁在负弯矩作用下的微段模型Fig.5 Infinitesimal element ofcomposite beam under negativebending moment
2.3计算模型
对组合梁交界面上的滑移进行分析,需建立微段变形模型,在两点对称集中荷载作用下的组合梁上取一长度为dx的微段,如图5所示.图5中:yr,ysc分别为钢筋合力点和钢箱(包括内填混凝土)合力点到组合梁交界面的距离;s为微段组合梁交界面上的滑移.
2.4滑移刚度
根据假设,单位长度上纵向水平剪力v与滑移s的关系为

(2)
式(2)中:p为栓钉间距;K为剪切刚度,即

(3)

2.5滑移解析解
根据组合梁微段模型的受力平衡关系,可得到钢梁与混凝土交界面的滑移微分方程[12],即
(4)
简支梁计算模型,如图6所示.竖向剪力V(x)根据不同的荷载作用情况进行取值,文中所对应的两点在对称集中荷载作用下,取值为

图6 简支梁计算模型Fig.6 Model of simply supported beam
(5)
对应工况下弯剪段、纯弯段的滑移解析解分别为
(6)
对式(6)求导,即可得出弯剪段、纯弯段滑移应变分别为
(7)
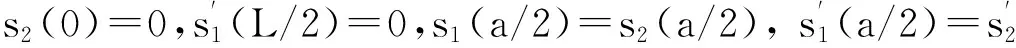
(8)
3 弹性承载力分析
3.1弹性阶段的截面应变分布
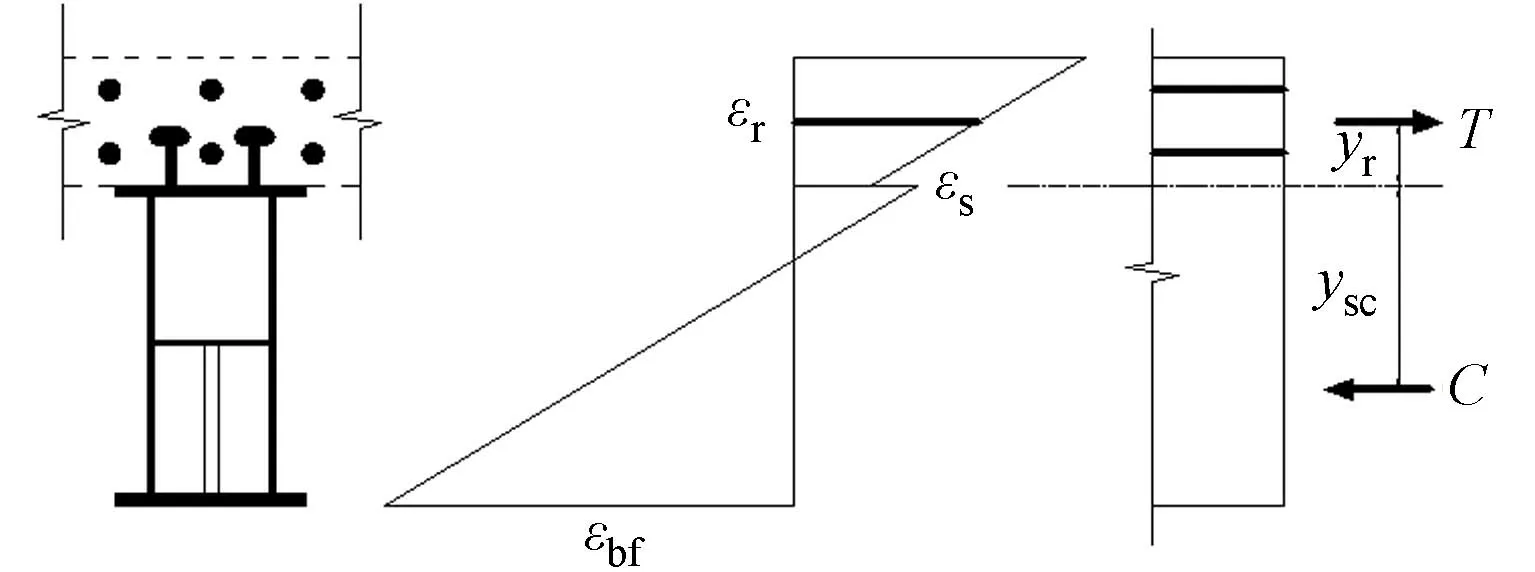
图7 组合梁截面计算模型Fig.7 Calculation model of composite section
负弯矩区的部分充填式钢箱-混凝土组合梁受拉翼板会产生开裂,在弹性承载力极限状态下,开裂后的混凝土退出工作,组合梁的承载力由纵向钢筋、钢箱和钢箱内填充的混凝土承担.当钢箱底板或纵向钢筋达到屈服应变时,即认为组合梁截面达到弹性承载力极限状态.在组合梁的交界面存在滑移效应时,其负弯矩区的弹性应变分布,如图7所示.图7中:εr为钢筋合力点处纵向应变;εbf为钢箱底板应变纵向压应变;T为钢筋收到的拉力;C为钢箱梁受到的压力.
3.2滑移效应影响下的弹性极限承载力
1) 钢梁首先屈服组合梁的弹性承载力表示为
(9)
式(9) 中:y0=ysc+yr;Msc为钢箱梁承担的弯矩,即
(10)
式(10)中:f为钢材屈服强度;Msc为截面换算后的填充混凝土和钢箱组合的截面抵抗矩.
由图7中应变分布的关系,根据式(1),(2),组合梁在弹性极限状态时满足关系式,即
(11)
式(11)中:h0为组合梁底部到钢筋形心的距离;Isc为截面换算后的填充混凝土和钢箱组合的截面惯性矩,可用平行移轴定理求出.
由于钢筋和钢箱的弹性模量差值只有3%左右,此处为了公式的简化忽略其差别,统一用E表示.联立式(9),(10),(11),可得出组合梁弹性承载力的表达式,即
(12)
取εs=0即为按完全剪力连接.不考虑滑移效应时的弹性抗弯承载力为
(13)
Meu,0和Meu的差值ΔMeu则为考虑滑移效应后组合梁的弹性抗弯承载力下降值,即
(14)
2) 设钢筋屈服强度为fy,钢筋屈服时,承受的拉力如图7所示,根据水平向受力平衡,得
(15)
同样,根据应变分布关系和假定(1),(2),有
(16)
联立式(9),(15),(16),解得
(17)
考虑滑移效应的弹性抗弯承载力下降值
(18)
式(18)为负值,说明当钢筋先于钢梁底板屈服时,组合梁截面的弹性抗弯承载力有所增大.但这种情况下钢梁下翼缘通常已经屈服,因此,从设计安全的角度出发,滑移效应影响下,组合梁的弹性抗弯承载力应主要考虑钢箱梁底板首先屈服的情况,并按式(12)进行计算.文中3个试件同为钢箱底板首先屈服也证明了这一点.由式(14)可知,组合梁截面的弹性抗弯承载力下降程度只由截面特性及滑移应变的大小决定,而钢筋和钢材的屈服强度对其没有影响.
4 理论计算值与试验值对比
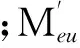

表4 抗弯承载力计算结果与实测结果对比
5 结论
1) 滑移效应对部分充填式钢箱-混凝土组合梁的承载力的影响不能忽视,它会引起截面弹性抗弯承载力的降低,按换算截面法计算的弹性抗弯承载力值偏大.文中推导出考虑滑移效应的弹性抗弯承载力计算公式,并将计算结果与试验实测值进行对比,发现两者吻合良好,验证了公式的准确性.
2) 在抗剪连接程度相同时,随着配筋率的提高,组合梁的弹性抗弯承载力下降程度逐渐增大.
3) 通常以工字钢为钢梁的钢-混凝土组合梁,其负弯矩区的弹性抗弯承载力下降程度一般达到15%以上[13],而文中所述的部分充填式钢箱-混凝土组合梁下降程度只有15%左右,证明了该截面形式在受力性能上的优势,在设计中可以考虑采用.
[1]钟新谷,舒小娟,郑玉国,等.钢箱-混凝土组合梁正截面承载力的初步研究[J].土木工程学报,2002,35(6):73-79.
[2]莫时旭,郑艳,钟新谷,等.钢箱-混凝土组合梁受力性能有限元分析[J].广西大学学报(自然科学版),2010,35(4):543-548.
[3]舒小娟,钟新谷,沈明燕,等.钢箱-混凝土组合梁初步设计与应用[J].土木工程学报,2011,44(增刊1):8-16,37.
[4]钟新谷,舒小娟,沈明燕,等.钢箱-混凝土组合梁正截面强度设计理论与试验研究[J].中国工程科学,2008,10(10):47-53.
[5]羊海林,莫时旭,郑艳,等.部分充填混凝土窄幅钢箱组合梁抗弯承载力[J].广西大学学报(自然科学版),2015,40(1):11-18.
[6]羊海林,莫时旭,郑艳,等.部分充填混凝土窄幅钢箱组合梁抗裂性能研究[J].广西大学学报(自然科学版),2014,39(4):1441-1447.
[7]聂建国,沈聚敏.滑移效应对钢-混凝土组合梁弯曲强度的影响及其计算[J].土木工程学报,1997,30(1):31-36.
[8]XUA Rongqiao,WU Yufei.Two-dimensional analytical solutions of simply supported composite beams with interlayer slips[J].International Journal of Solids and Structures,2007,44(1):165-175.
[9]GIRHAMMAR U A.A simplified analysis method for composite beams with interlayer slip [J].International Journal of Mechanical Sciences,2009,51(7):515-530.
[10]胡少伟,叶祥飞.预应力连续组合梁负弯矩区抗弯承载力分析[J].工程力学,2013,30(11):160-165.
[11]中华人民共和国国家标准.钢结构设计规范: GB 50017-2003[S].北京:中国计划出版社,2003:113.
[12]聂建国,樊健生.组合梁在负弯矩作用下的刚度分析[J].工程力学,2002,19(4):33-36,28.
[13]张旭宏.负弯矩作用下钢-混凝土简支组合梁的滑移效应分析[D].哈尔滨:哈尔滨工程大学,2007:12.
(责任编辑: 陈志贤 英文审校: 方德平)
Effects of Slip on Flexural Capacity of Partially Filled Steel Box Composite Beam
BAN Zhipeng1,2, JIANG Xue1, ZHENG Yan1, XU Haining1
(1. Guangxi Key Laboratory of Rock-Soil Mechanics and Engineering, Guilin University of Technology, Guilin 541004, China;2. College of Civil Engineering and Architecture, Guilin University of Technology, Guilin 541004, China)
In order to analyze the elastic flexural capacity of negative bending moment regions of partially filled steel box composite beam under the influence of the slip. Infinitesimal element of simply supported composite beams under the two-points symmetric reverse loading is established, and the differential equation of slip is derived to study solutions of slip and slip strain, the formula of elastic flexural capacity is deduced further by the means of the strain distribution of composite sections. The two-points symmetric reverse loading experiment on three composite beams are carried out to validate the accuracy of the formula, and the test results are in good agreement with the calculated results, indicating that the elastic flexural capacity of composite beam decreases significantly by the adverse effect of slip.
partially filled steel box composite beam; negative moment regions; slip; elastic flexural capacity
10.11830/ISSN.1000-5013.201605009
2015-09-23
郑艳(1973-),女,副教授,博士,主要从事组合桥梁结构行为的研究.E-mail:253651988@qq.com.
国家自然科学基金资助项目(51168011, 51108109); 广西岩土力学与工程重点实验室科研课题资助项目(11-CX-05)
TU 398; TU 375.1
A
1000-5013(2016)05-0570-06

