高原环境下电子时间引信炸点控制修正方法

李豪杰,云赛英,李长生,王伟强

(南京理工大学 智能弹药国防重点学科实验室,南京 210094)



高原环境下电子时间引信炸点控制修正方法

李豪杰,云赛英,李长生,王伟强

(南京理工大学 智能弹药国防重点学科实验室,南京 210094)

针对海拔高度变化对电子时间引信炸点精度有重要影响的问题,提出了一种电子时间引信作用时间对高原环境的自适应修正方法。该方法利用引信作用时间改变量随海拔高度的变化关系,得出不同射程时的海拔修正系数,进而修正引信的装定时间。以80 mm火箭弹为例,仿真实验表明,在利用该文修正方法修正后,不同海拔处的引信炸点位置精度在全射程范围内均小于2 m;而不修正时,在海拔高度为4 750 m,打击400 m目标时,引信炸点误差可达22 m。该研究结果对平原射表的高原应用有很重要的意义,使电子时间引信在高原的炸点精度得到提高。

引信;高原;时间修正;炸点精度

随着世界形势和作战对象的变化,以及各种先进电子设备的发展,现代战争对电子时间引信空炸炸点位置的精度要求越来越高。影响引信炸点位置精度的因素不仅与电子时间引信本身的定时精度等有关,还与电子时间引信装定时间的精度即火控解算的时间精度有关。目前,我国火控解算都是基于以低海拔靶场的试验结果为基础编制的平原射表。由于我国四大高原约占国土总面积的1/4,这就决定了弹箭可能在0～5 000 m的高度范围内使用,而弹箭所受空气动力与空气的密度、压力、温度和黏性等因素有关,这些因素又随着弹丸飞行高度而变化[1],装定时间均基于平原射表,这必然会带来引信装定时间本身的误差,进而造成引信的炸点误差。文献[2]和文献[3]对平原和高原环境下弹丸外弹道的差异进行了分析,提出了提高高原射表精度的必要性,并通过计算得到随着海拔提高地面密集度提高等特点。文献[4]指出在实际发射条件下,实际初速与标定初速之间存在的偏差导致引信炸点误差并给出了相应的修正方法,但并没有考虑电子时间引信受海拔高度的影响带来的引信作用时间的误差。查阅资料,笔者未发现目前针对高原条件对电子时间引信空炸炸点精度影响的研究。为此,本文研究海拔高度变化对电子时间引信炸点精度的影响,提出一种电子时间引信作用时间对高原环境的自适应修正方法。

1　弹道模型

为分析不同海拔高度对弹丸运动的影响,需建立弹丸的运动方程。对于飞行稳定性良好的弹丸,章动角δ很小,采用质点弹道基本上接近实际弹道。基于以下基本假设:

①弹体为刚体,忽略弹性;

②地面坐标系为惯性坐标系;

③地表面为平面,忽略地球曲率影响。

建立的弹丸质心运动方程如下[5]:

其中:

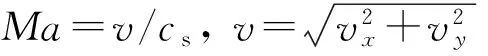
ρ=p/(R1τ),R1=287.05,

G(v,cs)=4.737×10-4cx,on(Ma)v,

C=id2×103/m。

式中:Ma为马赫数;v为弹丸飞行速度;vx,vy分别为弹丸水平分速和弹丸垂直分速;g为重力加速度;cs为声速;τ为按标准大气条件计算的虚温;h(y)为密度函数;ρ为空气密度;ρon=1.206 kg/m3;p为大气压强;R1为常系数;cx,on(Ma)为1943年阻力定律;C为弹道系数;i为1943年阻力定律的弹形系数;d为弹丸直径;m为弹丸质量。

阻力系数与空气的密度、压力、温度和黏性等因素直接相关,而这些因素又与弹丸的飞行高度有关。所以,阻力系数随高度会发生变化,且在亚音速时,阻力系数随高度增加,高度增加10 km,阻力系数增量可大于10%。此处,假设阻力系数随海拔高度线性增加,海拔每增加250 m,阻力系数按0.25%增加[4]。

2　海拔高度对引信炸点位置的影响

利用Matlab/Simulink软件,基于四阶、五级龙格库塔法构建弹丸的质心运动模型,解算在不同海拔条件下到达指定射程时弹丸所需的理论飞行时间与装定时间的改变量Δt以及对应的射程差ΔX。

以某80 mm火箭弹为例,利用上述弹道模型,计算各海拔高度对引信炸点位置的影响程度。初始输入条件如表1所示。表中,v0为初速度,θ0为射角。

表1　80 mm火箭弹弹道仿真的初始条件

表2列出了弹丸在各海拔高度上射击一定距离目标时,通过弹道模型计算的理论飞行时间与在海平面射击时引信的装定时间之差Δt,表3为由此时间差带来的射程差ΔX,表中,h为海拔高度,X为射程。从表中可以看出,装定时间的误差随着海拔高度和射程的增加均呈现增大的趋势。而且可以看出,在5 000 m海拔处打击400 m处目标时,将有176 ms的误差,以及23.96 m的射程误差。这对于电子时间引信来说影响是很大的,精度完全不能满足要求。

为直观分析上述时间差和射程差随海拔高度的变化规律,作图如图1、图2所示。

如图1和图2所示,时间差和射程差随海拔高度的增加均呈现线性增加的趋势,且随着打击距离的增加,其误差也将增大。上述规律将为在不同海拔高度射击时修正引信作用时间提供依据。

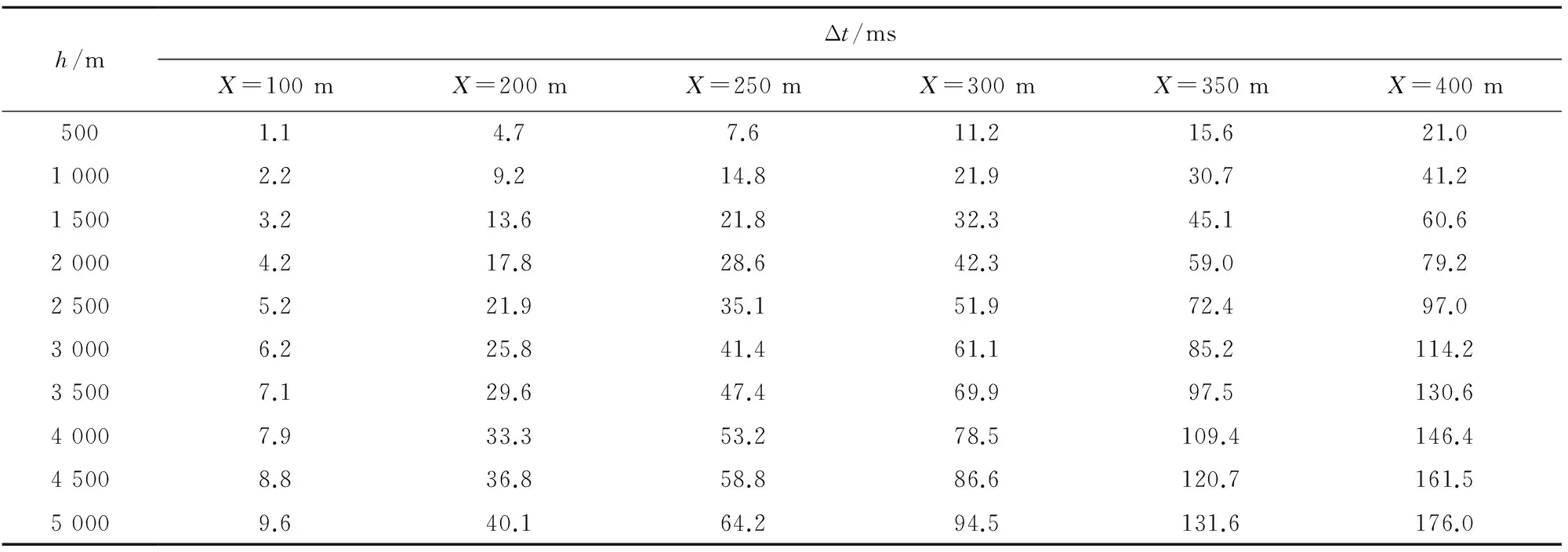
表2　各海拔高度理论飞行时间与海平面的装定时间差

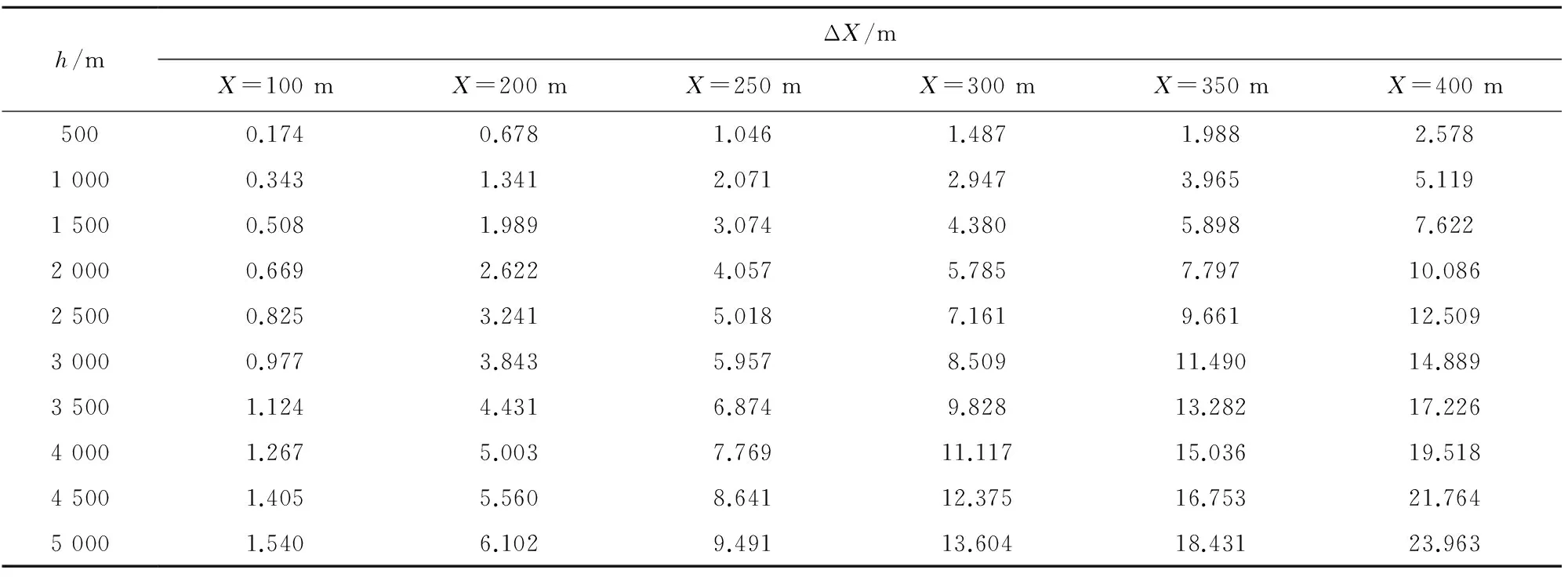
表3　各海拔高度理论射程与海平面射程的射程差

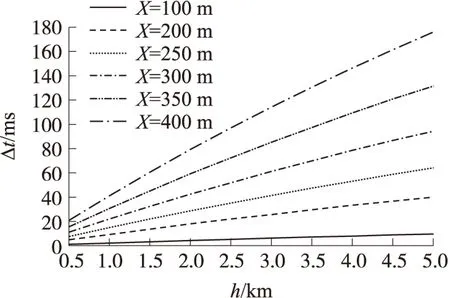
图1　时间差随海拔高度的变化曲线

图2　射程差随海拔高度的变化曲线

3　修正方法及验证

3.1时间修正方法

从前述的分析可以看出,在不同的海拔高度打击一定距离的目标,采用平原射表解算的作用时间对引信进行装定,将带来较大的时间差,进而导致炸点误差。此项误差是由于平原环境射击与高原环境射击的差异导致的利用平原射表对电子时间引信进行装定的不准确造成的。该误差属于系统误差,是可以通过补偿来减小的误差。而且,利用传统的高程测量方法如精密水准测量、三角水准测量以及气压测量的方法,能够得到海拔高度的值,现在有了全球定位系统等各种新型光电设施,可以通过各种光电信号方便地算出高程,即得出当地海拔高度。从上面分析可知,时间误差随海拔的变化近似为线性,即Δt随海拔高度h呈线性变化。所以提出了如下的时间修正公式:

Δt=f(h)=kh

(1)

th=t0-Δt

(2)

式中:k为不同海拔高度修正时间变化量的系数；t0为在海平面时到达指定射程时的理论弹道计算出来的时间;Δt是在不同的海拔高度与t0有相同射程时的时间差值，也即修正时间;th是在不同的海拔高度与t0有相同射程时按上述拟合方法修正后的时间值。

在对引信装定前,通过弹道解算,得到不同海拔高度修正时间变化量的系数k,制作成表格,在实际发射时,只需要通过查表,便可以对由于海拔变化而引起的引信作用时间变化量进行修正。

3.2仿真实验验证

同样,利用第2节的初始条件,通过分析Δt随海拔高度h的变化规律,得出上述时间修正方法中的修正系数k。利用最小二乘拟合法对上述Δt随h的变化曲线进行拟合,得到在打击不同距离目标时的修正系数k,如表4所示。拟合所得常数项很小,可以忽略,在此不予考虑。

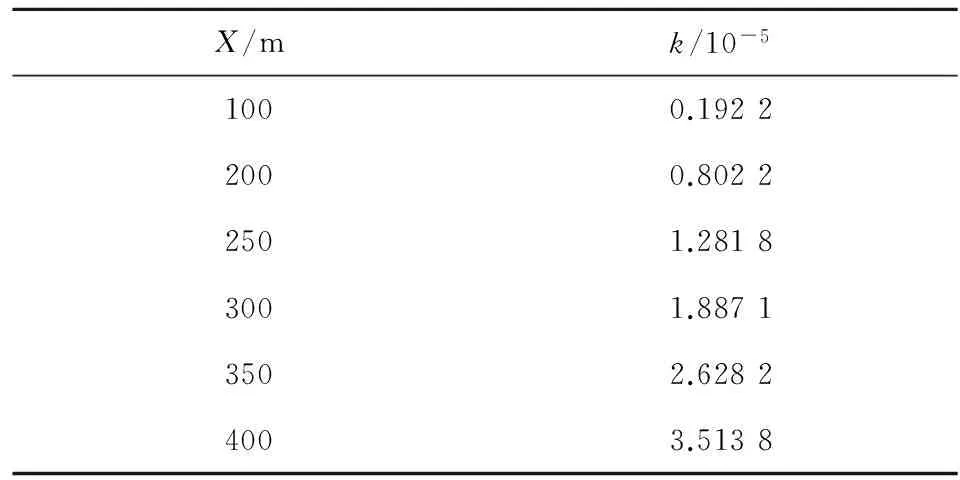
表4　不同射击距离时的修正系数

选取几个海拔高度值,利用上述时间修正方法对弹丸的装定时间进行修正,分析修正前与修正后的引信作用时间和炸点精度,以打击200 m目标和400 m目标为例,结果如表5、表6和图3所示,表中,t1是在不同海拔飞到预定射程时的理论弹道计算时间,Δt1是在各海拔高度理论弹道计算值与利用修正公式修正后的时间差值,ΔX1是Δt1对应的射程差。Δt2是在不同海拔高度未进行修正的理论弹道计算时间与装定时间的差值,对应的射程误差为ΔX2。

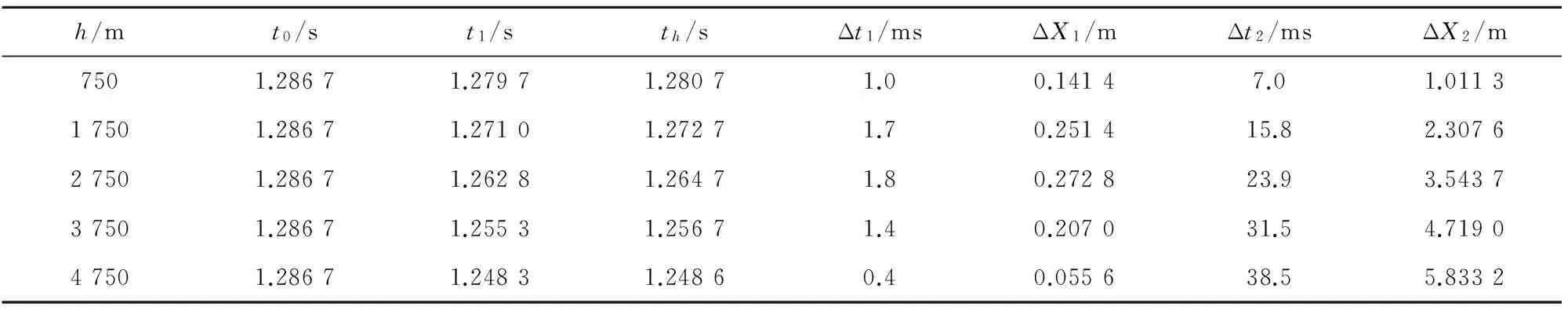
表5　X=200 m,k=0.802 2×10-5的实验数据

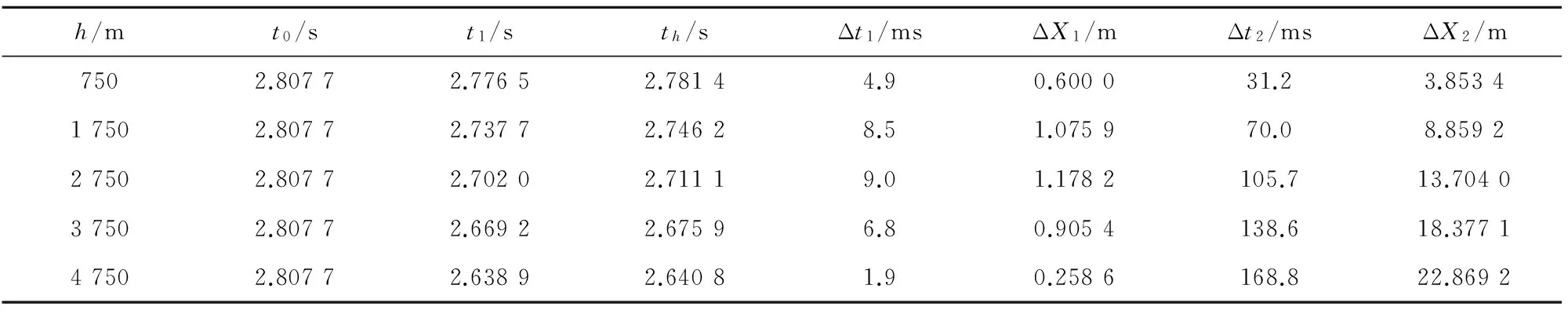
表6　X=400 m,k=3.513 8×10-5的实验数据

图3　修正与不修正时射程误差随海拔高度的变化曲线

从表5和表6以及图3可以直观地看出,利用上述修正方法对在不同海拔高度射击时的引信作用时间进行修正后,引信的炸点位置误差明显减小,在海拔4 750 m处射击400 m距离目标时,射程误差从22.9 m下降到0.3 m,效果明显。从而可以得出,利用上述方法进行修正后,可以不考虑由于海拔不同带来的时间引信的炸点误差,这对平原射表在高原地区的通用性方面有很重要的意义。

3.3试验验证

以80 mm火箭弹为例,在海拔5 050 m根据表4的修正系数进行射程400 m的验证试验,试验结果如表7所示。表中,Xr为实际射程,ΔX为海拔5 050 m实际射程与理论射程的射程差。

表7　h=5 050 m,400 m射程的实验数据

分析表7可得,在加入时间修正后,弹丸在海拔5 050 m的射程误差在5 m内,而根据海拔高度5 050 m、射程400 m所装定的时间,在零海拔下对应的射程为360 m。从而可以得出,平原射表应用于高原必须进行修正,而本文提出的自适应修正方法对平原射表应用于高原具有重要意义。

4　结论

本文研究了不同海拔高度对电子时间引信空炸炸点位置的影响,提出了对不同海拔高度引信装定时间的修正方法。该方法利用引信作用时间改变量随海拔高度的变化关系,得出不同射程时的海拔修正系数,进而修正引信的装定时间。以80 mm火箭弹为例,仿真实验表明,在利用上述修正方法修正后,不同海拔高度处的引信炸点位置精度在全射程范围内均小于2 m,而不修正时,在海拔为4 750 m,打击400 m目标时,引信炸点误差可达22 m。比较修正与不修正的结果可以看出,本文提出的对海拔高度的自适应修正方法对引信炸点精度的提高有很好的效果。本研究结果对平原射表的高原应用有很重要的意义,使在高原作战时的空炸炸点精度明显提高。

[1]钱明伟.火炮武器高原射表编制理论研究[D].南京:南京理工大学,2008.

QIAN Ming-wei.Research on the theory of firing table design at high altitude for artillery systems[D].Nanjing:Nanjing University of Science and Technology,2008.(in Chinese)

[2]王良明,钱明伟.高原环境对高炮外弹道特性的影响[J].弹道学报,2006,18(1):18-21.

WANG Liang-ming,QIAN Ming-wei.Effects of plateau environment on the ballistics of anti-aircraft guns[J].Journal of Ballistics,2006,18(1):18-21.(in Chinese)

[3]钱明伟,王良明,郭锡福.火炮武器高原射击时的弹道特性研究[J].弹道学报,2009,21(4):21-25.

QIAN Ming-wei,WANG Liang-ming,GUO Xi-fu.Ballistic analysis for artillery systems firing on plateau[J].Journal of Ballistics,2009,21(4):21-25.(in Chinese)

[4]洪黎,张合,李豪杰,等.某单兵火箭弹作用时间自适应修正方法[J].仪器仪表学报,2013,34(8):1 917-1 920.

HONG Li,ZHANG He,LI Hao-jie,et al.Acting time adaptive correcting method of an individual rocket[J].Chinese Journal of Science Instrument,2013,34(8):1 917-1 920.(in Chinese)

[5]韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2008.

HAN Zi-peng.Exterior ballistics of projectiles and rockets[M].Beijing:Beijing Institute of Technology Press,2008.(in Chinese)

Correction Method of Burst Control of Electronic Time Fuze in Plateau Environment

LI Hao-jie,YUN Sai-ying,LI Chang-sheng,WANG Wei-qiang

(ZNDY of Ministerial Key Laboratory,Nanjing University of Science and Technology,Nanjing 210094,China)

The altitude change has an important influence on burst-point accuracy of electronic time fuze(ETF).Aiming at this problem an adaptive correction method of action time of ETF to the plateau environment was presented.In the method,the altitude correction coefficient at different ranges was obtained by using the relation of action-time change varying with altitude,and the fuze setting-time was corrected. Taking 80 mm rockets for instance,the simulation was carried out.The results show that the burst-point positional-accuracy of fuze at different altitudes in the whole range is less than 2 m by using correction methods;while not applying the correction methods,the burst-point error of fuze of rocket hitting 400 m-range targets reaches to 22 m at altitude of 4 750 m.The result is of great significance for plain-firing-table being applied in the plateau,and the accuracy of ETF burst-point in the plateau improves.

fuze;plateau;time correction;burst point accuracy

2016-04-02

李豪杰(1973- ),男,副教授,博士,研究方向为引信技术。E-mail:haojieli@njust.edu.cn。

TJ43

A

1004-499X(2016)03-0048-05