数学模型在体育比赛排名规则的制定问题中的应用①

周峰利徐文杰

（1.武汉体育学院经济与管理学院 湖北武汉 430079；2.十堰市张湾区炉子小学 湖北十堰 442002）

数学模型在体育比赛排名规则的制定问题中的应用①

周峰利1徐文杰2

（1.武汉体育学院经济与管理学院 湖北武汉 430079；2.十堰市张湾区炉子小学 湖北十堰 442002）

随着国务院国发【2014】46号文件的出台，全国健身已经上升到国家战略，全国各种各样的体育比赛越来越多。针对越来越多的比赛，比赛规则制定尤为重要。该文主要讨论体育比赛排名规则的制定问题，并以篮球比赛为例，在比赛通用的总积分法的基础上，通过分析其优劣性，运用数学模型，给出特征向量法、概率法等比赛排名方法。

比赛排名 数学模型 特征向量法 概率法

现在人们对自身健康问题越来越重视，人们喜欢把业余时间花在体育锻炼上，促使越来越多的比赛应运而生，有比赛就必然涉及到排名问题，有些比赛，名次排列往往比较简单，因为涉及的团队较少，数据不复杂；而大多数的比赛涉及的团队较多，数据较为复杂，排名的影响因素就会很多，由于这些因素的影响，人们往往会对比赛结果产生质疑。为了解除人们的疑惑，一个公平透明的排名规则显得尤为重要。我们要建立一个可以克服诸多不确定因素的模型，使得排名结果能准确地反映球队的真实实力。

排名目的是根据比赛成绩排出反映各队的真实实力状况的一个顺序，所以说一个好的排名算法应满足下面的一些基本要求。

（1）保序性。我们认为各队的真实实力水平在综合成绩表中反映出来，所以根据排名的目的，要求排名顺序与成绩表所反映的各队真实水平是一致的。

（2）稳定性。成绩表中微小的变动不会对排名造成巨大影响，即球队发挥水平的较小波动性不会对排名结果产生大的影响。

（3）能够准确的进行补缺：两个队之间没有打比赛，我们只为成绩表残缺，对于两队成绩的残缺，只能通过他们同其他队的比赛成绩判断他们实力水平的高低。

（4）能够判断成绩表的可约性，能够容忍不一致现象。

（5）对数据可依赖程度给出较为精确的描述。

1　模型的建立

1.1积分法

总积分法的排名是以总积分的多少来决定的。各队胜一场得2分，负一场得1分（包括比赛因缺少队员而告负），弃权得0分。计算各队在所有比赛中总的积分，按照总积分的高低来排出名次，总积分多的队伍名次列前。

表1　比赛结果发生的概率表（2场比赛）

如果遇到2支队伍总积分相等，则按积分相等两队相互间比赛的成绩来确定名次，胜者名次列前。如果遇到2支以上的队总积分相等，则按总积分相等队之间相互比赛的胜负场次来决定名次，胜利场次多的队伍名次列前。如果名次仍相等，则按他们之间比赛的得失分率大小决定名次，得失分率大的名次列前。如果仍然相等，再按他们在所有比赛中的得失分率来决定名次，得失分率大的名次列前。如果存在弃权的队伍，弃权的队伍名次并列最后，各队与弃权的比赛成绩均以“0”计算。

总积分法具有很大的局限性，很显然，总积分法对比赛场数多的队伍有利，为了克服这一缺点，可以采取平均积分法来对各支队伍来进行排名。平均积分法就是将每个队的总积分除以该队参加比赛的场数，得出每场平均积分，按各队平均积分的高低来排名，平均积分高的队伍名次列前。如果遇到2支队伍的平均积分相等，则按平均积分相等两队相互间比赛的成绩来确定名次，胜者名次列前。

如果遇到2支以上的队总积分相等，则按总积分相等队之间相互比赛的胜负场次来决定名次，胜利场次多的队伍名次列前。如果名次仍相等，则按他们之间比赛的得失分率大小决定名次，得失分率大的名次列前。如果仍然相等，再按他们在所有比赛中的得失分率来决定名次，得失分率大的名次列前。得失分率=每队的每场得分之和/每队的每场失分之和（对方的得分之和）×100%

但是，总积分法和平均积分法都存在着两个缺点：一是没有考虑对手的情况，胜第二名与胜最后一名是一样看待的；二是没有考虑胜负的程度，大胜对手和险胜对手没有差别。

1.2特征矩阵法

由于篮球比赛中不存在平局的情况，我们可以假设胜一局得到一个积分，负一局得到零个积分，由此建立一个N×N的邻接矩阵M，来表示各支队伍之间比赛的胜负情况，由此建立得分向量S 来表示各支队伍的胜负情况：其中称为一级得分向量，一级得分向量表示各支队伍的总得分情况。

由于比赛过程中存在总得分相同的队伍，所以，一级得分向量无法排出所有队伍的名次，需要进一步计算出高级的得分向量称之为二级得分向量，二级得分向量表示每支球队战胜的各个球队的得分之和，与一级得分向量相比，二级得分向量更有理由作为排名次的依据。继续这个程序，得到k级得分向量，K的值越大，用S（k）作为排名依据更合理，如果k趋向于正无穷时，收敛于某个极限得分向量（为了不使它无限变大，应进行归一化），那么就可以用这个得分向量作为排名次的依据。

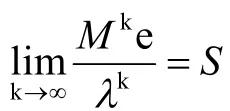
上面提出特征向量法，是建立了邻接矩阵M之后，求出M的对应于最大特征根的特征向量，作为代表各支队伍水平比的向量，以它作为依据来为各支队伍排名次。

以下我们还要提出进一步改进的模型，在此之前，我们需要考虑不同队伍之间比赛场次的差异，若两队之间进行了多场比赛，则将其之间的多场比赛的平均分来作为比赛的结果。两队之间进行的多场比赛，其结果能更真实地反映两队之间的相对水平，在此，我们引入比赛结果的可信度因子P，单场比赛的可信度为P，则N场比赛的可信度为，由此，两队之间进行的多场比赛可转化为单场比赛的平均得分。

邻接矩阵M中的元素mij可设为是Ti对Tj各场比赛转化为单场比赛后的平均得分，当Ti与Tj之间没有进行过比赛时，mij=0，即此时的邻接矩阵M可理解为得分矩阵，仔细观察又有不足之处。更合理的方法应满足以下方面。

1.3概率法

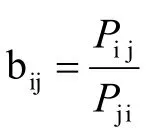
我们从若干场比赛的结果反推Pij和Pji，具体的方法为根据Ti在对Tj的各场比赛中的总得分来计算，主要思想为假如Pij，Pji预先给出了确切的值，则可以利用他们分别算出Ti在对Tj的各场比赛中的总得分的概率，由极大似然估计，假如Ti的实际得分为m分，就有理由认为Ti得m分的概率比得其他分的概率都大。

为计算Pij与Pji，我们将一场比赛的概念看成两个半场，不同于实际比赛中的半场，半场的结果仅有胜负之分，上下半场Ti，Tj各胜一个半场记为平局。

记Ti在一个半场中胜Tj的概率为q，则在一场比赛中，Ti胜Tj的概率为q2；Ti负于Tj的概率为（1-q）2；Ti平Tj的概率为2q（1-q）。

对两队进行一场，两场或者三场比赛的情况，分别按总积分多少分成若干的等级，根据假设，总积分数正好等于获胜的半场的数目，把它看作比较两队水平的一个度量，计算每一等级中所有比赛结果发生的概率，例如：两场比赛的情况根据表1数据就可明确知道比赛结果发生的概率。

根据极大似然估计的思想，如果某一等级的结果发生了，我们就应当以为两队水平之比处于该等级的概率比处于其他等级的概率要大。我们可以根据这一点，列出不等式并解除q的范围。例如：得分为3的结果发生时，应有不等式组，可以计算出对应赢球的概率。

2　结语

通过分析可知，模型的优点主要为：（1）能够较为准确的处理数据，对比赛的程序没有严格要求，稳定性很好，可以适用于任何赛制。（2）灵活性强，提供了对比赛数据可约性的正确评估，并且可以灵活调整比赛数据。（3）满足保序性，能够处理不同场次的权重，对数据可依赖程度给出较为精确的描述。

但此模型也有其存在的明显的不足之处为判断矩阵的计算较为复杂，当参赛队伍较多的时候求解判断矩阵会很费时。

［1］姜启源，谢金星，叶俊.数学模型［M］.北京：高等教育出版社，2011.

［2］于长锐.复杂决策问题的多元化模型体系研究［J］.管理科学学报，2004，7（2）：88-91.

［3］戚立峰，毛威，马斌.一个给足球队排名次的方法——B题［J］.教学实践与认识，1994（2）：87-94.

G80-05

A

2095-2813（2016）09（a）-0175-02

10.16655/j.cnki.2095-2813.2016.25.175

周峰利（1987—），男，汉，湖北黄冈人，硕士，助教，研究方向：体育、数学。