开尔文定理的一个注记及其应用
刘延柱
(上海交通大学工程力学系,上海 200240)
开尔文定理的一个注记及其应用
刘延柱
(上海交通大学工程力学系,上海 200240)
开尔文-台特-切塔耶夫定理中关于含保守力和陀螺力的线性系统稳定性条件指出:若保守系统不稳定,特征值无零根且具有偶数个正实根,则陀螺力的加入可使系统转为稳定.若正实根为奇数个,则加入陀螺力也不可能改变系统的不稳定性.定理不涉及有零根情形.作为开尔文定理的补充,本文基于二自由度系统证明:若保守系统不稳定,正实根为奇数个,且特征值存在零根,则陀螺力的加入也能使系统转为稳定.作为定理的实际应用,讨论匀速旋转的非惯性坐标系中的平衡稳定性问题.若将旋转坐标系中的离心惯性力视为有势力,则成为包含离心力势能的形式上的保守力场.由于受扰运动有科氏惯性力出现,此类系统与惯性参考系的保守力场并不等同,不允许应用拉格朗日定理以势能极小值条件判断其平衡稳定性.利用开尔文定理的上述补充条件,科氏惯性力的加入可改变此形式上保守系统的稳定性.以圆轨道二体系统和限制性三体问题的拉格朗日点的一次近似稳定性为例.仅考虑万有引力场和离心惯性力场,为含零根和一个正实根的不稳定保守系统.增加科氏惯性力项可使不稳定转为稳定.
开尔文定理,运动稳定性,旋转坐标系,科氏惯性力
引言
开尔文(Lord Kelvin)和台特(Tait PG)于1879年提出,后经切塔耶夫(Chetayev N G)严格证明的判断线性系统稳定性的定理指出:若保守系统不稳定,特征值无零根且不稳定度(具有正实根特征值的数目)为偶数,则陀螺力的加入可使系统转为稳定.若不稳定度为奇数,则加入陀螺力也不可能改变系统的不稳定性[1-7].定理不涉及有零根情形.本文基于二自由度系统证明:若保守系统不稳定,不稳定度为奇数,且特征值存在零根,则陀螺力的加入也能使系统转为稳定.似可作为开尔文定理中关于陀螺力影响保守系统稳定性的补充.
匀速旋转的非惯性参考系中的离心惯性力若视为有势力,则成为包含离心力势能在内的形式上的保守力场.但由于受扰运动中有科氏惯性力出现,此类系统与惯性参考系的保守力场并不等同.由于未考虑科氏惯性力因素,不允许应用拉格朗日定理以势能极小值条件判断其平衡稳定性.根据开尔文定理的上述补充条件,科氏惯性力的加入可使此形式上的保守系统从不稳定转为稳定.以圆轨道二体系统和限制性三体问题的拉格朗日点的一次近似稳定性为例.
1 开尔文定理的补充条件
定理:若保守系统不稳定,不稳定度为奇数,且特征值存在零根,则陀螺力的加入能使系统转为稳定.
证明:带陀螺力的二自由度保守系统线性化扰动方程的一般形式为

特征方程为

其中

如系统存在零根,则a4=0,即k1与k2的乘积为零.不失一般性,设k2=0,k1<0.无陀螺力时(g= 0)有正实根,保守系统不稳定,不稳定度为1.增加陀螺力后非零特征值为

2 匀速转动的非惯性参考系
在以角速度ωc匀速旋转的保守力场中运动的质点存在雅可比积分[3-4].

其中H为哈密顿函数,V为势能,T2为相对运动的动能,的负值为离心惯性力的势能.其中m为质点的质量,r为质点相对转动轴的距离. 将-T0与V之和作为修正势能(modified potential energy),记作V*[7].将保守力与离心惯性力合成的力场视为形式上的特殊保守力场,则匀速旋转的非惯性参考系与惯性参考系的保守力场即在形式上一致.雅可比积分可改写为

如质点处于相对平衡状态,则T2为零,V*必取驻值.质点受扰产生相对运动时,非零的动能T2为扰动速度的正定二次型.如V*为扰动的正定函数,则哈密顿函数H亦为正定.取H为李雅普诺夫函数,根据李雅普诺夫定理,非惯性系中的相对平衡稳定.V*的正定性条件即函数极小值条件.从而证明,修正势能V*在平衡位置处取孤立极小值为平衡稳定性的充分条件.拉格朗日定理似可扩展至匀速转动的非惯性参考系[1-3].
以上证明过程的数学推导虽无问题但理论根据有误.受扰运动由于坐标系旋转产生的科氏惯性力因不做功而与修正势能V*无关.以不含科氏惯性力因素的修正势能V*为依据不可能对稳定性做出正确判断.有关教材列举的用拉格朗日定理判断此类系统的典型例题为受旋转圆环约束的质点平衡稳定性.由于科氏惯性力与质点受约束的相对运动正交不影响稳定性判断仅为特例[1-3].一般情况下不允许利用拉格朗日定理判断匀速旋转非惯性系中的平衡稳定性.
3 二体系统的稳定性
作为最基本的天体力学问题,二体系统的稳定性已经受漫长历史的严格检验成为不争的事实,但很难给出简明的物理解释.圆轨道中的卫星作稳态运动时,万有引力与离心惯性力互相平衡.如卫星因扰动朝地球方向有微小位移,必导致万有引力增大,离心惯性力减小.如忽略受扰运动的科氏惯性力,其合力作用方向与扰动方向一致而趋向不稳定,与实际存在的稳定现象相悖.
以月球和地球组成的二体系统为例.设地球和月球的质量为m1,m2,质心O1与O2的距离为d,与系统的质心O点的距离a1,a2分别为

月球和地球分别绕O点作半径a1和a2的圆轨道运动.以O为原点,过O点的O1与O2连线为x轴,建立轨道平面坐标系(O-xy).设Gm2为地球和月球的引力参数,G为万有引力常数,(O-xy)的转动角速度ωc可利用地球对卫星的引力与离心力,或卫星对地球引力与离心力的平衡条件解出
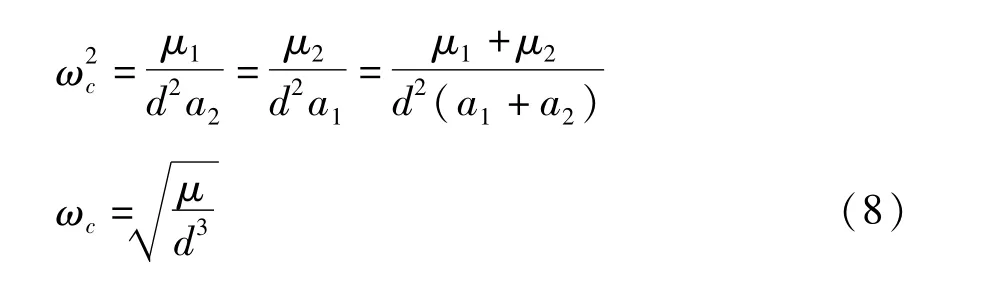
其中μ=μ1+μ2.因m1≫m2,可近似认为总质心O与地球质心O1重合.设月球质心O2受扰后的位置坐标为x,y,与O点的距离为(图1).此系统的修正势能V*为

将平衡状态的坐标以下标s表示,即xs=d,ys=0.采用一次近似稳定性判断方法,考虑科氏惯性力,列出卫星在(O-xy)中相对运动的动力学方程

令

代入方程组(10),仅保留 ξ,η的一次项,化作线性化扰动方程

其中

如略去方程组(11)中的科氏惯性力项,将式(12)代入后导出特征方程


除零根λ=0表示卫星沿轨道切线方向的随遇性平衡以外,纯虚根λ=±iωc表示指向地球方向的稳定平衡,受扰运动为频率ωc的周期运动.科氏惯性力的引入使不稳定保守系统转为稳定.

图1 二体系统Fig.1 Two-body system
4 拉格朗日点的稳定性
小质量物体在二体引力场中运动,忽略其对引力场影响的动力学问题在天体力学中称为限制性三体问题,例如飞船在地球-月球引力场中的轨道运动.仍利用二体系统的参考坐标系(O-xy),质量为m的飞船P在地月引力场中的修正势能为

其中ρ1,ρ2为飞船P与O1和O2的距离(图2).

图2 地月系统中的飞船位置Fig.2 Position of the spacecraft in Earth-Moon system

令修正势能V*对x,y的偏导数为零,解出小物体在地月引力场中的5个相对平衡位置Li(i=1,2,…,5),称为拉格朗日点(Lagrangian points)[3,6-7].其中 L1,L2,L3分布在x轴的(-a1,a2),(a2,∞),(-∞,-a1)区间内,L4,L5与地球O1和月球O2构成边长为d的等边三角形(图3).

图3 拉格朗日点Fig.3 Lagrangian points
为判断L4,L5的平衡稳定性,计算V*对x,y的二阶偏导数,令

得到

其中 δ=m2/(m1+m2).飞船P在平衡位置附近的线性化扰动方程与式(11)相同,仅其中m2以飞船质量m代替.将式(17)代入,如略去科氏惯性力项,导出的特征方程与式(13)相同,特征值含一个零根和一个正实根保留科氏惯性力,特征方程变为

解出特征根

导出λ的纯虚根条件,即一次近似稳定性条件

即要求Δ≤0.0385,或 m2≤0.0385(m1+m2).将地球和月球的质量数据代入,算出δ=0.012,此条件得到满足.证实科氏惯性力的加入使拉格朗日点L4,L5从不稳定转为稳定[7-10].
在上述二体系统和拉格朗日点的稳定性分析中,式(12)和(17)中修正势能 V*的二阶偏导数均小于或等于零,不满足V*的极小值条件.不可能也不允许用拉格朗日定理判断其平衡稳定性,但不满足拉格朗日定理的平衡状态未必不稳定.对线性化扰动方程所做的稳定性分析由于存在零根而属于临界情形,也不能确定原非线性系统的稳定性,但可作为对二体问题或拉格朗日点等实际稳定性现象的近似解释.
5 结论
1)作为开尔文定理的补充,有零特征根和奇数个正实根的不稳定保守系统也能借助陀螺力转为稳定.
2)匀速旋转的非惯性参考系如将离心惯性力作为保守力,形式上可视为含离心力势能的特殊保守系统.由于忽略坐标系旋转导致的科氏惯性力,一般情况下不允许应用拉格朗日定理判断此特殊保守系统的平衡稳定性.
3)作为陀螺力的科氏惯性力对匀速旋转非惯性系稳定性的影响遵循开尔文定理的补充规律.对圆轨道二体问题和拉格朗日点的一次近似稳定性的分析证实上述论断.
1 王照林.运动稳定性及其应用.北京:高等教育出版社,1992(Wang Z L.Stability ofmotion and its applications,Beijing:High Eucation Press,1992,in Chinese)
2 舒仲周,张继业,曹登庆.运动稳定性.北京:中国铁道出版社,2001(Shu Z Z,Zhang JY,Cao D Q.Stability of motion,Beijing:China Railway Publishing House,2001 (in Chinese))
3 刘延柱.高等动力学.北京:高等教育出版社,2001 (Liu Y Z.Advanced dynamics.Beijing:High Education Press,1992(in Chinese))
4 ЧетаевНГ.УстоȞчивостьдвижения.М.Гостехиздат,1950(王光亮译.运动稳定性.北京:国防工业出版社,1959)(Chetayev N G.Stability ofmotion,Moscow:National Technical Press,1950,(in Russian))
5 МеркинДР.Гироскопическиесистемы.М.Гостехиздат,1956(MerkinDR.Gyroscopicsystem,Moscow:National TechnicalPress,1950(inRussian)
6 Kreisel M K.Theorie und anwendungen.Berlin:Springer-Verlag,1971(中译本:贾书惠等译.陀螺,理论与应用.北京:国防工业出版社,1983(in Chinese))
7 Meirovitch L.Method of analytical dynamics.New York:McGraw-Hill,1970
8 Rimrott F P J.Introductory orbit dynamics.Braunschweig:Vieweg&Sohn,1989
9 Breakwell J,Pringle Jr R.Resonances affecting motion near the Earth-Moon equilateral libration points.Progress in Astronautics&Aeronautics,1966,17:55~74
10 Leiphltz H.Stability theory.New York:John-Wiley,1987
A NOTE OF THE THEOREM OF LORD KELVIN AND ITS APPLICATION
Liu Yanzhu
(Department of Engineering Mechanics,Shanghai Jiao Tong University,Shanghai 200240,China)
According to the theorem of Lord Kelvin,an unstable conservative system can be stabilized by the gyroscopic force when the number of positive real characteristic roots is even without zero characteristic roots.In this paper,it is proved that an unstable conservative system with zero characteristic roots and an odd number of positive real characteristic roots can also be stabilized by the gyroscopic force.As an application of the theorem of Lord Kelvin,the stability problem in a non-inertial reference frame rotating with constant angular velocity is also discussed.The rotating coordinates system is regarded as a formal conservative system with potential energy including the field of centrifugal inertial force.But the rotating system is notequivalent to the conservative inertial system,because there exists the Coriolis inertial force in perturbed motion.Therefore,the Lagrange theorem of minimal potential energy is not allowed to determine the stability in the formal conservative system.However,when the complimentary condition of Kelvin′s theorem is employed,the unstable formal conservative system can be stabilized by the Coriolis inertial force.The stability problems of two-body system with circle orbit and the Lagrange points of restrict three-body problem are analyzed as examples.Both systems under the action of gravitational and centrifugal force are unstable with one zero and one positive real characteristic root.When the Coriolis inertial force is considered,both unstable systems can be changed to be stable.
theorem of Lord Kelvin,stability theory,rotating coordinates system,coriolis inertial force Received 26 March 2015,revised 22 April 2015.
E-mail:liuyzhc@163.com
10.6052/1672-6553-2015-027
2014-03-26收到第1稿,2014-04-22收到修改稿.
E-mail:liuyzhc@163.com
——以开尔文公式为例

