保护性看跌期权策略在50ETF指数的应用

李响

（郑州大学数学与统计学院，河南郑州450000）

保护性看跌期权策略在50ETF指数的应用

李响

（郑州大学数学与统计学院，河南郑州450000）

本文基于布莱克-肖期权定价模型，对保护性看跌期权策略、再平衡理论进行了研究。将保护性看跌期权策略应用于50ETF指数，并在实证分析中创新性地融入了再平衡操作，资金曲线与相关指标分析表明该策略在降低投资风险、提高收益方面具有显著效果。

布莱克-肖模型；期权；再平衡；保护性看跌期权策略；50ETF指数

投资是以获得收益为目的，但在实现长期目标过程中资金会有波动和各种风险，为了控制投资组合的资金风险、提高投资组合收益，人们把各种投资策略用于交易过程，保护性看跌期权策略以其低风险、稳健收益的特点被投资人广泛使用。

1　布莱克-肖期权定价模型

1973年，Fisher Black和Myron Scholes建立了布莱克-肖模型，奠定了期权定价的理论基础［1，2］，该模型可以为已知期限的任何金融工具进行理论报价。

模型的基本假设为：①标的资产为股票，股价服从几何布朗运动；②市场无套利机会；③无风险利率为已知常数；④交易可连续进行；⑤市场无摩擦，整个交易过程中无交易税费；⑥对卖空没有如保证金等的任何限制；⑦标的股票无股息，不分红。

根据假设，股票价格S遵循数学家伊藤提出的伊藤过程，即ds=μsdt+σsdz

其中μ是连续复利的年预期收益率，可设为常数；σ为股票价格的年波动率，也可设为常数；dz=ε dt为维纳过程，ε为标准正态分布中取得的一个随机值，t为时间。

假设变量f是S和t的某种函数，则

构造一个证券组合，定义其价值

选取Δ使得Π是无风险的，再根据无套利原理，可以得到：

上式即是Black-Scholes微分方程，此方程有多个解，其中对于欧式看跌期权的边界条件是：

t=T，f=max（X-S，o）

求解此边界条件下的该微分方程，可得到欧式看跌期权价格p的计算公式为：

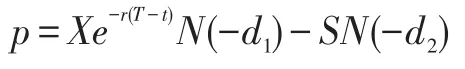
其中

其中S表示股票价格，X表示期权价格，T表示期权的期限，t表示当前时间，r表示连续复利的无风险利率，σ表示股票价格的波动率，函数Nd（X）表示标准正态分布的累积概率分布函数。

2　交易及操作策略

在布莱克-肖模型的基础之上，John C.Hull研究讨论［3］了多种涉及各方面的期权交易策略。其中，期权与其他资产相结合的交易策略有：保本债券、单一期权与股票的策略、差价、组合策略等等。

2.1保护性看跌期权交易策略

保护性看跌期权交易策略属于持有单一期权与股票的策略，它是在持有标的资产多头的同时，买入相应的看跌期权［3］。当期权到期时有两种情况：股票价格高于期权执行价格，期权不行权，股票收益减去权利金即为该策略的收益；反之，期权行权，以执行价格卖出手中的股票，损失为权利金。可以看出，该策略可能的最大盈利无上限，可能的最大亏损为期权的权利金，其盈亏平衡点出现在股票价格与执行价格之差和权利金相等时。

另外，股票持有者选择什么样的看跌期权也至关重要。一般来说，交易者应该选择买入略微虚值的看跌期权作为标的资产的保护。一手虚值看跌期权的成本很小，但却可以起到对保护股票的正面作用与限制盈利的负面作用之间达到一种平衡［4］。

2.2再平衡操作

再平衡就是对资产组合进行动态管理、维持资产各类别的目标配置比例，以便控制组合的风险水平，产生额外收益，使组合的实际配置符合长期目标［5］。

若投资组合中股票、债券和现金的最优配比分别为m、n、q（m+n+q=1），随着各资产价格的变动，其在总资产的比例也会发生变化。以股票为例，假设第二天股票在总资产中的比例从m上升到m1，那么就应该卖出相应的股票，使股票在总资金中的占比重新降为m。另外，为了控制成本，再平衡操作使用的频率也需加以考虑，可以规定其上下限，即“阈值”。

3　保护性看跌期权策略在50ETF指数上的实证分析

实证分析中，50ETF指数选用2015年3月至2015年12月的数据（本文所有的数据均从彭博客户端下载），策略操作过程如下:

①设定的初始资金为W，由标的资产和现金来构成资产组合，其中用于购买标的资产即50ETF指数的资金占初始资金的百分比为a，剩余的现金占初始资金的百分比为b（a+b=1）。

②买卖期权需支付的权利金从现金中出资，不考虑50ETF指数与期权的交易费用和保证金，无风险利率为3%。

③再平衡操作阈值设置为y1；与之相类似，设置期权平仓操作的阈值设定为y2。

④当50ETF指数在总资产中的比例发生变化并达到阈值y1时进行再平衡操作。

⑤在买入指数的同时买入相应的虚值看跌期权，取50ETF指数每日的收盘价作为当日指数的价格，假设初始时刻指数的价格为S0，t时刻指数的价格为St，初始时刻买入指数的同时选取期限为一个月，执行价格为K=（1-y2）S0的期权买入。

⑥在持有的过程中，若指数价格的涨幅或者跌幅超过y2，则平仓手中的期权，重新买入执行价格为K=（1-y2）St的期权。

⑦若从买入期权至交割日前5天的这段时间内，指数的价格没达到平仓期权的阈值y2，则在交割日前5天时，平仓手里的期权，再买入下个月相应的看跌期权。

将上述过程用MATLAB实现，当w=1000万、a=40%、b=60%、y1=0.004、y2=0.1时，得到不使用任何操作和策略的50ETF指数、加入再平衡操作的50ETF指数以及加入再平衡后再使用保护性看跌期权策略的50ETF指数的相关指标如表1，资金曲线如图1：

表150ETF指数的相关指标

从表1可看出，与不使用任何操作和策略及仅使用再平衡操作相比，再平衡中加入保护性看跌期权保险策略时，年化收益率和夏普比率都有了显著提高，而作为描述风险的指标年化标准差，以及最大亏损比率、总亏损天数、连续亏损天数和最大回撤比例都明显下降。这种变化趋势从图1也可看出：再平衡中加入保护性看跌期权保险策略的长期收益最高、资金曲线波动最小，即风险明显降低。

图150ETF资金曲线

调整参数（w、a、b不变）使y1=0.001、y2=0.2，结果如表2、图2。

表2　50ETF指数的相关指标

对比表1和表2及图1和图2可看出：第二组参数设置下，使用再平衡和保护性看跌期权策略后的各项指标、资金曲线波动均优于第一组，说明该策略的应用效果与参数设置密切相关。

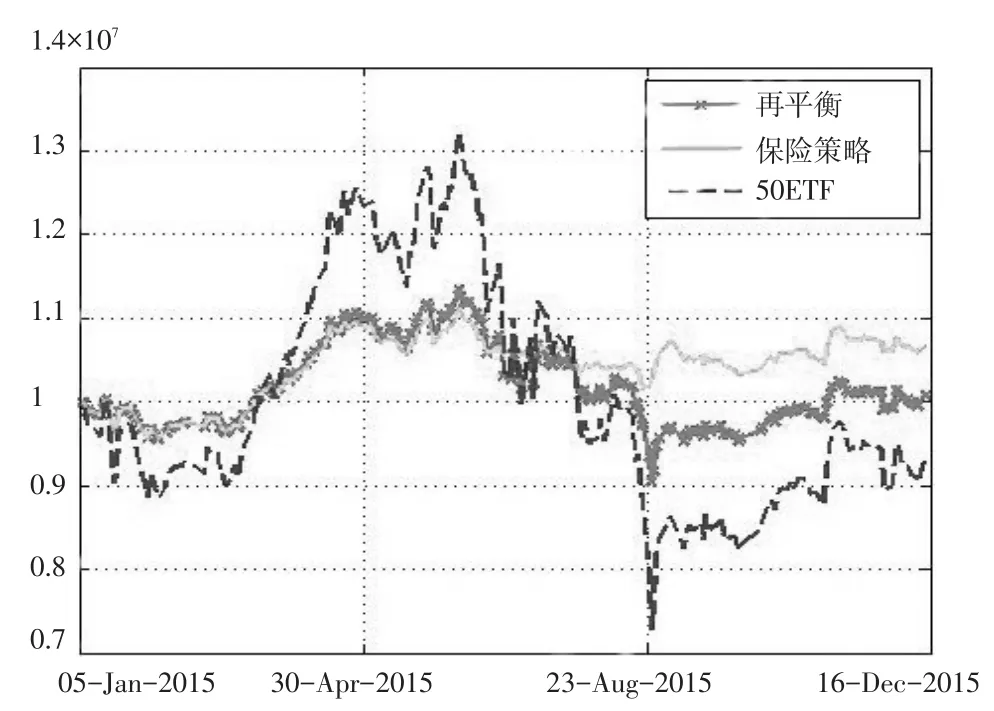
图250ETF资金曲线

4　结论

保护性看跌期权策略对控制投资组合的风险水平、实现长期投资目标、提高投资组合收益率有很好的效果。该策略应用于50ETF指数表现良好，年化收益率和夏普比率都有了显著的提高，年化标准差、最大亏损比率、总亏损天数、连续亏损天数和最大回撤比例都明显下降，资金曲线波动变小；此外，保护性看跌期权策略的应用效果还与参数设置有关。

［1］Fischer Black，Myron Scholes.The Pricing of Options and Corporate Liabilities［J］.The Journal of Political Economy，1973（3）:637-653.

［2］Fischer Black，How We Came Up with the Option Pricing Formula［J］.Journal of Portfolio Management，1989（2）：154-158.

［3］约翰·赫尔（John C.Hull），王勇，索吾林.期权、期货及其他衍生产品［M］.北京：机械工业出版社，2014.

［4］劳伦斯·麦克米伦（Lawrence G.McMillan），郑学勤。期权投资策略［M］.北京：机械工业出版社，2010.

［5］大卫·斯文森（David F.Swensen）机构投资者的创新之路［M］.北京：中国人民大学出版社，2010.

The Application of Protective Put option Trading Strategy to 50ETF Index

Li Xiang
（School of Mathematics and Statistics，Zhengzhou University，Zhengzhou Henan 450000）

This paper based on the Black-Scholes option pricing model，studied the protective put option trading strategy and rebalance theory.It also applied the protective put option trading strategy to the 50ETF index and creatively added rebalance operation to this strategy in the process of empirical analysis.Through the analysis of capital curve and the related indicators，this trading strategy has been found out that it had significant effects in reducing the investment risk and ensuring the income.

Black-Scholes model；Option；Rebalance；Protective put option trading strategy；50ETF index

F830.9

A

1671-0037（2016）08-37-3

2016-7-2

李响（1993-），女，本科，研究方向：金融数学。