从“知识的形成过程”来命题
——以“圆面积公式的推导与应用”为例
江苏丹阳市华南实验学校 殷中华
从“知识的形成过程”来命题
——以“圆面积公式的推导与应用”为例
江苏丹阳市华南实验学校殷中华
小学数学命题应当体现知识的迁移、转化、应用,重视知识技能形成过程的考查,突出数学的实践和运用,引导探究、创新的学习风气,引导教师加强知识形成过程的教学。
在推导圆面积时,课本上是把一个圆形纸片剪拼成一个以半径为宽的近似的长方形,在这一转化过程中,周长发生了变化,面积没有变。也就是说,长方形的周长比圆的周长要多出2条半径的长度,长方形的面积等于圆的面积。围绕这个“推导转化和应用”的过程,可以从考查“学生知识形成过程的角度”来设计试题,下面举例来说。
例1.在推导圆面积时,把一个圆形纸片剪拼成一个近似的长方形,通过测量,这个长方形的周长比原来圆的周长多16厘米,原来这张圆形纸片的面积是()平方厘米。
【设计意图:学生首先要明确,把一个圆形纸片剪拼成一个近似的长方形,长方形的周长比圆的周长要多出2条半径的长度,即2条半径等于16厘米,那么半径就是8厘米,圆的面积就是:3.14×82=200.96(平方厘米)】
例2.下面是一个圆平均分成若干份后拼成的一个近似长方形,该圆的面积是()平方厘米。

【设计意图:学生首先要明确,把一个圆形纸片剪拼成一个以半径为宽的近似的长方形,长方形的长就是圆周长的一半,12.56÷3.14=4(厘米),半径就是4厘米,那么圆的面积就是:3.14×42=50.24(平方厘米)】
例3.将圆平均分成若干个小扇形,剪拼成一个近似的长方形。(如下图)
如果长方形的长是6.28厘米。
(1)圆的面积是多少?
(2)阴影部分面积是多少?
(3)阴影部分周长是多少?

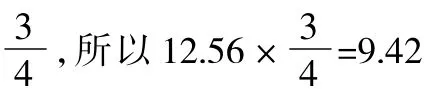
例4.(1)如图1所示,正方形的边长是2厘米,在它里面画了一个最大的圆,这个圆的面积是()平方厘米。圆的面积占正方形面积的()。

(2)如图1所示,正方形的边长是8厘米,在它里面画了一个最大的圆,这个圆的面积是()平方厘米。圆的面积占正方形面积的()。
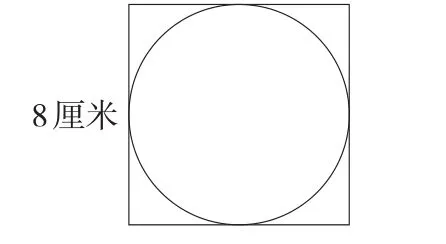
图2
(3)自己在另一张纸上再任意举一个这样的例子。计算出圆的面积为(),正方形的面积为(),圆的面积占正方形面积的()。
(4)将上面得到的三个分数都化成分母是100的分数,然后比较它们的大小,你发现了什么?由此你得到了什么结论?
(5)应用上面得到的结论,计算:在一个边长为120分米的正方形内画一个最大的圆,该圆的面积是()平方分米。(只要列出算式)
【设计意图:充分展现数学规律形成与发展的过程,以及规律的应用过程,引导学生去概括规律,积极探索、发现和运用规律,从中培养和考查学生的观察、比较、抽象、概括能力。这样习题的设计给学生提供猜想、尝试、探索、发现规律或模型的思考空间,使学生从小养成善于猜想、积极探索的学习精神,拓展思维,培养能力】♪

