钢框架截面受损时静力稳定性分析

张曙光，吴　涛

(1.长春工程学院土木工程院，长春 130012； 2.吉林省土木工程抗震减灾重点实验室，长春130012)



钢框架截面受损时静力稳定性分析

张曙光1，2，吴涛1

(1.长春工程学院土木工程院，长春 130012； 2.吉林省土木工程抗震减灾重点实验室，长春130012)

建立钢框架结构有限元分析模型，通过特征值屈曲分析与非线性屈曲分析，获得钢框架在静荷载作用下的理论屈曲荷载以及极限荷载。对比分析无损钢框架与底层梁柱腹板、翼缘受损时的钢框架的静力稳定性，得出底层柱翼缘处受损更容易引起结构发生静力失稳的结论。

钢框架结构；静力稳定性；截面受损；有限元分析

0　引言

钢结构失稳是指结构在微小的力的作用下就会使结构或其组成构件产生很大位移，从而丧失承载力。钢结构失稳就其性质而言，分为平衡分岔失稳、极值点失稳和跳跃失稳。跳跃失稳是指结构由一种平衡状态跳跃到另一种平衡状态。当达到第一次平衡状态时，结构已经失去承载能力，后面的平衡状态已经没有意义，故可以等同为极值点失稳的类型。由于实际的结构受到了双重非线性以及初始缺陷的影响，大多数失稳类型属于极值点失稳。而平衡分岔失稳是基于理想的结构，未考虑双重非线性及初始缺陷。因此，求解过程相对简单，同时，求解的临界荷载可为非线性屈曲分析提供参考，所以平衡分岔失稳在理论分析中显得尤为重要。

1　结构稳定分析的判定准则

对整体稳定以及整体稳定判定准则进行研究发现当前钢框架结构整体稳定判定准则主要有以下3个观点[1]：1)荷载—位移曲线顶点判定准则；2)承荷极限判定准则；3)曲线切线斜率判定准则。本文主要通过曲线切线斜率判定准则对结构稳定性进行判定，即当荷载—位移曲线斜率为0时判定框架达到稳定临界状态[2]。

2　结构稳定分析的有限单元法

2.1特征值屈曲分析

特征值屈曲分析用于预测结构发生第一类失稳时分岔点的临界荷载，通过荷载与位移的关系式，对线弹性荷载状态{P0}进行求解

{P0}=[Ke]{u0}。

(1)

假设线弹性状态时变形很小，在任意状态下{P0}、{u}、{σ}增量平衡方程由式(2)给出

{Δp}={[Ke]+[Kσ(σ)]}{Δu}，

(2)

式中：{u0}为施加载荷{P0}的位移结果；{σ}为与{u0}对应的应力；[Ke]为线弹性刚度矩阵；[Kσ(σ)]为某应力状态{σ}下计算的初始应力刚度矩阵，即几何刚度矩阵[KG]。

假设加载行为是外加荷载{P0}的线性函数

{p}=λ{p0}，

(3)

{u}=λ{u0} ，

(4)

{σ}=λ{σ0}。

(5)

则可得

[Kσ(σ)]=λ[Kσ(σ0)]，

(6)

则前屈曲范围内增量平衡方程为

{Δp}={[Ke]+λ[Kσ(σ0)]}{Δu}。

(7)

在结构变得不稳定即{Δp}=0时，结构产生位移{Δu}，前屈曲范围内的增量平衡方程通过式(8)给出

{[Ke]+λ[Kσ(σ0)]}{Δu}=0。

(8)

为了使式(8)成立 ，必须有

det{[Ke]+λ[Kσ(σ0)]}=0。

(9)

在有限元模型中，系统发生屈曲时相应变形的叠加由特征向量{Δu}n进行表示，通过式(9)计算得出λ的最小值，即为弹性临界载荷{Pcr}。

2.2非线性屈曲分析

非线性屈曲分析用一种逐渐增加荷载的分析技术来求得使结构开始变得不稳定时的临界荷载[1]。非线性有限元方程的求解一般都是通过迭代法来完成的，迭代法分为Newton-Raphson法、修正的Newton-Raphson法和弧长法[3]。

Newton-Raphson法具体步骤如下[1]：

1)以增量形式逐级施加荷载；

2)在每一荷载增量中通过平衡方程的迭代来使荷载增量达到平衡；

3)求解平衡方程

[KT]{Δu}={F}-{Fnr}，

(10)

式中:[KT]为切线刚度矩阵；{Δu}为位移增量；{F}为外部荷载增量；{Fnr}为内部力向量。

切线刚度矩阵是进行非线性屈曲分析时，判定结构稳定性能的依据。切线刚度矩阵[KT]由式(11)给出

[KT]=[Ke]+[Kd]+[KG]，

(11)

式中：[Ke]为线弹性刚度矩阵；[Kd]为大位移刚度矩阵；[KG]为几何刚度矩阵。

4)进行迭代，直到{F}-{Fnr}在允许的范围内。

Newton-Raphson法通过线性求解，检查收敛性,反复这种迭代过程直到满足收敛准则。Newton-Raphson法计算过程烦琐，为了简化计算的复杂度，修正的Newton-Raphson法在迭代过程中每次所使用的切线刚度矩阵总是采用它的初始值。对某些不稳定的非线性静力分析，如果只使用Newton-Raphson方法，结构始终不能够收敛，通常使用弧长法来获得稳定求解。其求解方法是通过引入了一个附加的未知项——屈曲因子λ(-1<λ<1)，由式(12)给出力的平衡方程

[KT]{Δu}=λ{F}-{Fnr}，

(12)

为了容纳附加的未知项，引入约束方程式(13)

(13)

荷载因子λ和位移增量{Δu}通过弧长半径l关联起来。

3　结构截面损伤后的静力稳定性有限元分析

3.1模型建立

建立一个6层钢框架有限元分析模型，如图1所示，长宽为6 000 mm×6 000 mm，层高3 900 mm，建筑总高度23.4 m。梁柱采用Q235 H型钢,楼板采用混凝土楼板，强度等级为 C30，板厚150 mm，板内钢筋HPB300。基本风压 0.65 kN/m2，地面粗糙程度为B类。考虑结构自重、梁上线荷载9 kN/m、楼面活荷载2 kN/m2、水平风荷载。

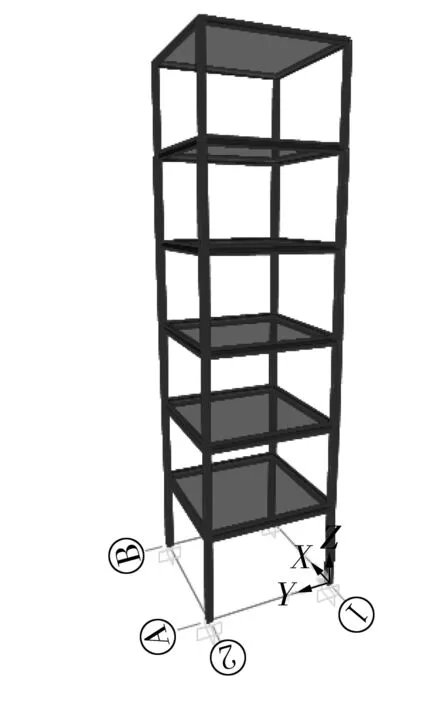
图1　钢框架模型

据不同的截面损伤建立4种工况下的有限元分析模型：工况1：结构无损伤；工况2：结构底层柱腹板受损，通过减小底层柱腹板厚度来模拟结构损伤；工况3：结构底层柱翼缘受损，通过减小底层柱翼缘厚度来模拟结构损伤；工况4：结构底层梁柱翼缘均受损，通过减小底层梁柱翼缘厚度来模拟结构损伤。

3.2梁柱构件截面参数

工况1：无截面损伤情况，截面参数见表1。

表1　工况1截面参数

工况2：结构底层柱腹板受损，截面参数见表2。

表2　工况2截面参数

工况3：结构底层柱翼缘受损，截面参数见表3。

表3　工况3截面参数

工况4：结构底层梁柱翼缘均受损，截面参数见表4。

表4　工况4截面参数

3.3无损钢框架结构有限元分析

3.3.1无损钢框架特征值屈曲分析

对钢框架进行特征值屈曲分析，定义活荷载2 kN/m2和风荷载0.65 kN/m2为施加给结构的基本荷载，同时放大风荷载和楼板活荷载，获得结构失稳时的临界荷载。提取前四阶屈曲模态，如图2～5所示。

图2　第一阶屈曲模态

图3　第二阶屈曲模态

图4　第三阶屈曲模态

图5　第四阶屈曲模态

由4阶屈曲模态变形图可以看出，结构顶层的水平位移最大，取柱顶部结点joint13的荷载—位移曲线作为结构是否达到极限承载力的判断依据。

由于在进行特征值屈曲分析过程中对结构施加1倍的基本荷载，获得第一模态的特征值屈曲因子为21.8，即结构失稳时临界荷载为21.8倍的基本荷载。构件在制作、运输、焊接以及施工安装等方面的不当操作会导致结构存在初始缺陷，因此，应将基本荷载放大23倍进行非线性屈曲分析。

3.3.2无损钢框架结构非线性屈曲分析

通过非线性屈曲分析获得的子步—位移关系曲线如图6所示。

图6　无损钢框架结构子步—位移曲线

图6中，横坐标表示结构柱顶点沿X轴水平位移；纵坐标表示有限元软件分析的荷载子步，进行非线性屈曲分析时设置的23倍基本荷载分为500荷载子步逐级增加，每子步对应0.046倍的基本荷载，荷载—位移曲线每点的切线斜率对应结构处于该状态时的刚度。由图可知，由于受到结构双重非线性的影响，风荷载和楼板活荷载逐渐增大，结构的刚度不断降低，当达到94子步，即风荷载和楼板活荷载增大到基本荷载的4.32倍时，结构荷载—位移曲线趋于水平，由结构稳定性判定准则可知，结构失稳的极限荷载为4.32倍基本荷载。

3.4结构截面受损条件下有限元分析

工况2结构底层柱腹板受损子步—位移关系曲线如图7所示。

由图7可知，随着风荷载和楼板活荷载逐渐增大，结构的顶点位移也随之增大，当达到83子步，即风荷载和楼板活荷载增大到基本荷载的3.82倍时，结构荷载—位移曲线斜率趋近于0，由结构稳定性判定准则可知，结构失稳时的极限荷载为3.82倍基本荷载。与无损的钢框架结构分析结果对比，结构底层柱腹板受损后在静荷载作用下的极限承载能力降低了11.7%。

工况3结构底层柱翼缘受损子步—位移关系曲线如图8所示。

由图8可以看出，随着风荷载和楼板活荷载逐渐增大，框架顶点位移也随之增大，当达到74子步，即风荷载和楼板活荷载增大到基本荷载的3.4倍时，结构荷载—位移曲线斜率趋近于0，由结构稳定性判定准则可知，结构丧失整体稳定性的极限荷载为3.4倍基本荷载。

与无损钢框架分析结果对比，结构底层柱翼缘受损后在静荷载作用下的极限承载能力降低了21.3%。由此可以看出，结构底层柱翼缘损伤的程度对结构的极限承载能力影响较大，在设计和施工过程中应该加以重视。

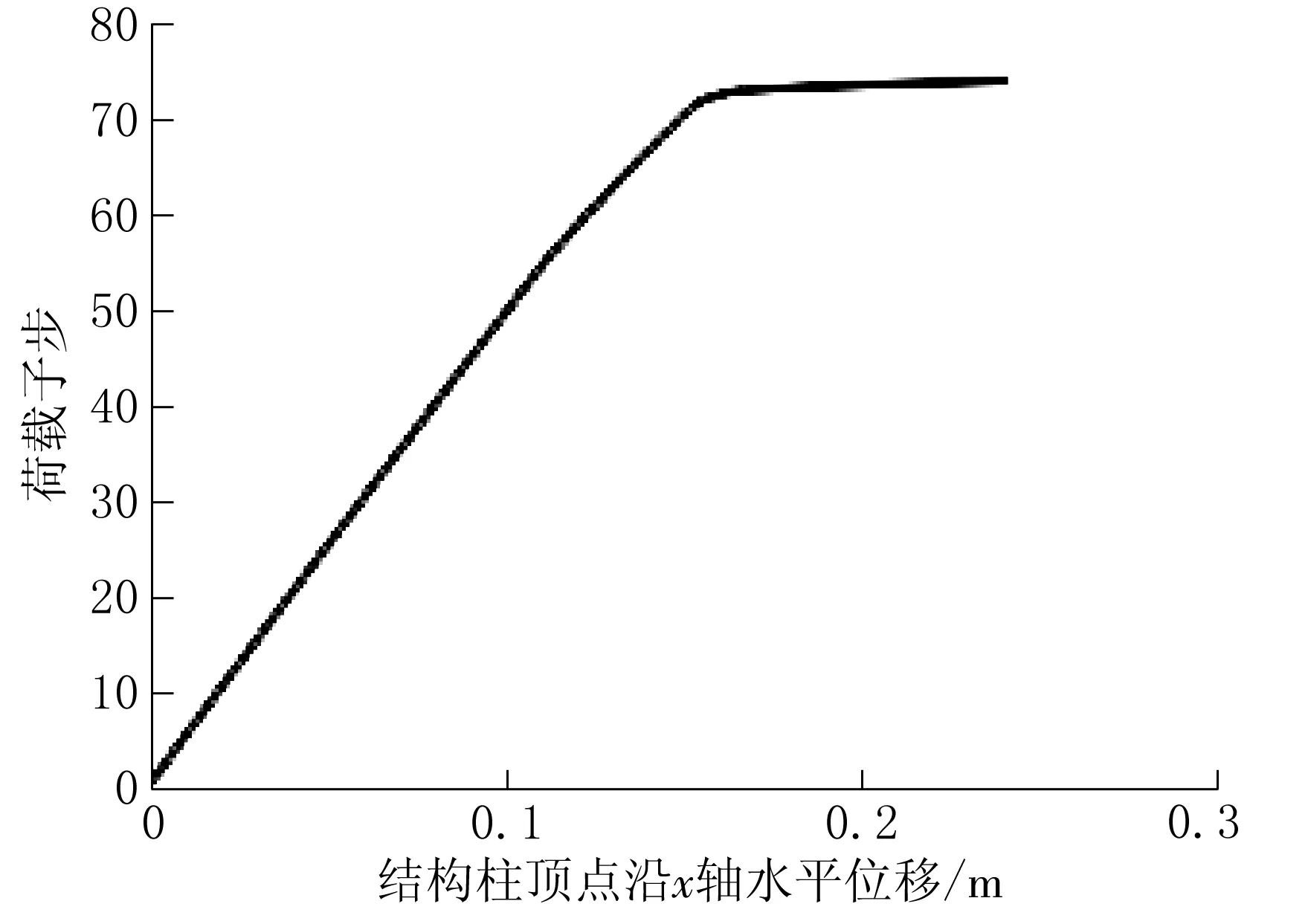
图8　底层柱翼缘受损钢框架结构子步—位移曲线

工况4框架底层梁柱翼缘均受损子步—位移关系曲线如图9所示。由图9可以看出，随着风荷载和楼板活荷载逐渐增大，结构的顶点位移也随之增大，当达到71子步，即风荷载和楼板活荷载增大到基本荷载的3.27倍时，结构荷载—位移曲线斜率趋近于0，由结构稳定性判定准则可知，结构失稳时的极限荷载为3.27倍基本荷载。

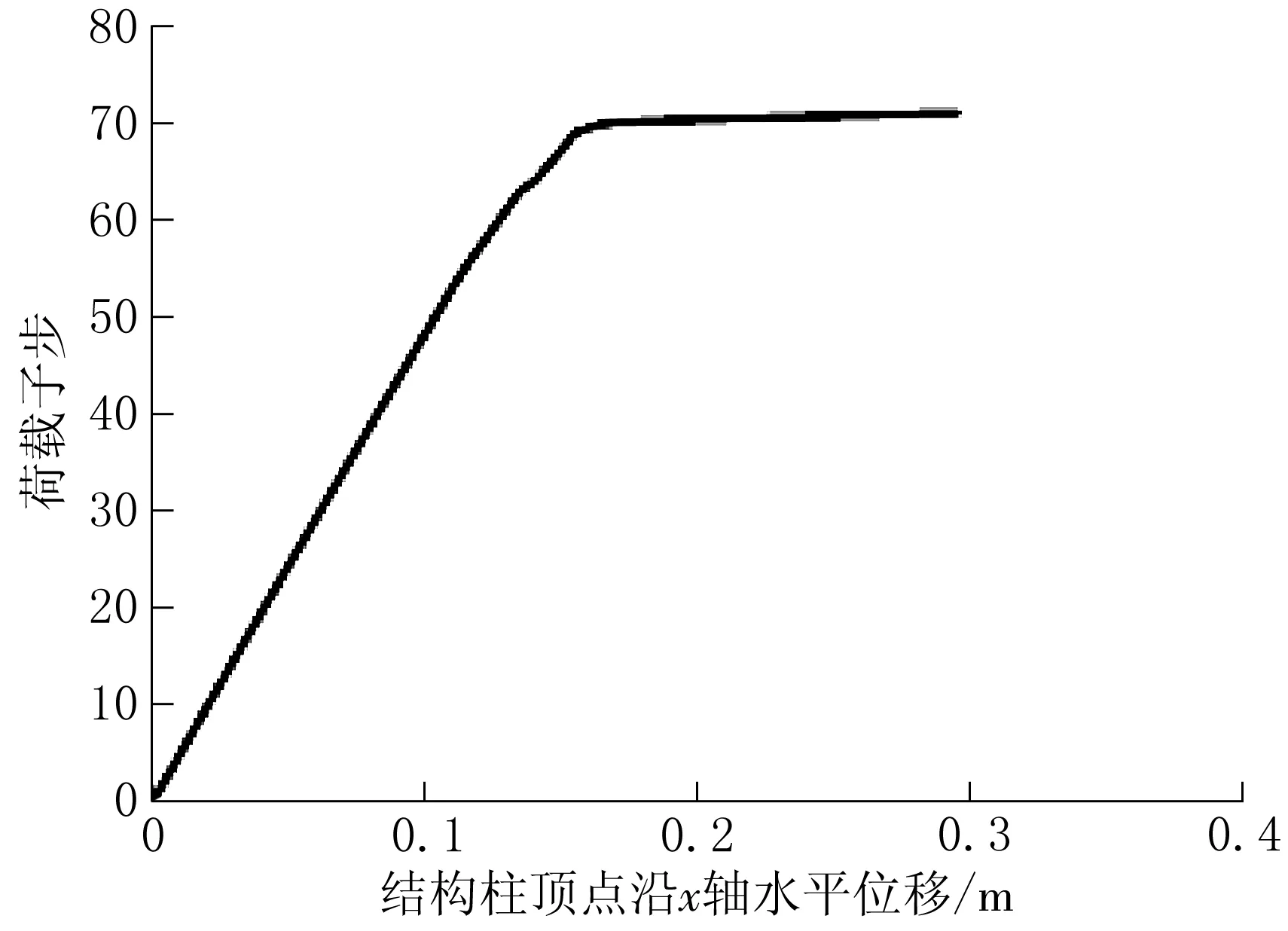
图9　底层梁柱翼缘受损钢框架结构子步—位移曲线

与无损的钢框架分析结果对比，结构底层柱翼缘受损后在静荷载作用下的极限承载能力降低了24.5%。与底层柱翼缘受损的钢框架结构分析结果对比可知，结构底层柱翼缘受损后在静荷载作用下的极限承载能力降低3.8%。由此可见，底层梁翼缘的损伤程度对钢框架结构整体稳定性影响不大。

4　结论

通过对比分析4种不同工况下钢框架结构在静荷载作用下对结构稳定性的影响，得出如下结论：

1)对比工况二与工况一可以得出，钢框架柱的腹板截面尺寸的改变对结构在静荷载作用下的极限承载能力影响明显，底层柱腹板厚度减小35.7%，结构极限承载能力降低了11.7%。

2)对比工况三与工况一可以得出，钢框架柱的翼缘截面尺寸的改变对结构在静荷载作用下的极限承载能力影响最为显著，底层柱翼缘厚度减小21.4%，极限承载力降低了21.3%。因此，在设计和施工过程中应该加以重视。

3)对比工况四与工况一可以得出，在静荷载作用下底层梁柱翼缘均受损后，即底层梁柱翼缘厚度分别减小27.3%和21.4%，结构极限承载力降低了24.5%；

4)对比工况四与工况三可以得出，底层梁柱翼缘均受损后的结构极限承载能力降低了3.8%。因此，底层梁翼缘的损伤程度对钢框架结构整体稳定性影响不大。

[1] 董庆.高层钢框架结构整体稳定性研究[D].南京：南京林业大学,2012.

[2] 孙哲.复杂钢框架结构非线性整体稳定分析[D].武汉：华中科技大学,2007.

[3] 万金国.钢结构非线性分析方法研究及其在软件中的实现[D].武汉：武汉大学,2010.

[4] 边旭辉.高墩大跨连续刚构桥施工与控制技术[D].西安：长安大学,2009.

[5] 王建强.大吨位桥式起重机结构参数化三维设计与性能分析[D].太原：太原科技大学,2014.

[6] 李谦.于家堡站双螺旋线单层网壳结构分析[D].天津：天津大学,2010.

[7] 曾涛,王俊平,汪胜辉.浅谈钢拱结构的稳定[J].山西建筑,2008(2):92-94.

[8] 李艳敏.冷弯薄壁型住宅墙柱体系轴向性能研究[D].西安：长安大学,2007.

The Analysis to Static Stability with Damage of Steel Frame Cross Section

ZHANG Shu-guang，etc.

(SchoolofCivilEngineering，ChangchunInstituteofTechnology，Changchun130012，China)

Based on the finite element analysis model of steel frame structure，the theoretical buckling load and ultimate load of steel frame under the effect of static load are obtained by eigenvalue buckling analysis and nonlinear buckling analysis.Compared with the static stability of the nondestructive steel frame structure，the bottom of beam-column web，and the steel frame with flange damaged，the conclusion that the bottom of the column flange damage is easier to make the structure more prone to static instability has been drawn.

steel frame structure；static stability；damage of cross section；finite element analysis

10.3969/j.issn.1009-8984.2016.03.001

2016-06-23

吉林省自然科学基金项目(20130101050JC)

张曙光(1968-)，女(汉)，吉林白山，教授，博士

主要研究结构优化设计。

TU392

A

1009-8984(2016)03-0001-05