行业工资差异的分位数回归分析*——以重庆市为例

徐　洁, 杨宜平

(重庆工商大学 数学与统计学院， 重庆 400067)



行业工资差异的分位数回归分析*
——以重庆市为例

徐洁, 杨宜平

(重庆工商大学 数学与统计学院， 重庆 400067)

首先考察了重庆市2000年至2013年农林牧渔业、建筑业等10个行业的工资数据分布特征,然后分别应用均值回归和分位数回归建模方法对重庆市行业工资差异状况进行了分析,以期发现在不同分位数下影响行业工资差异的关键因素以及它们对行业工资差异的贡献大小,并提出了解决重庆市行业工资差异的相关政策和建议。

分位数回归；均值回归；行业工资差异；显著性

从现有文献看,有关行业间的工资差异研究取得了一定的进展。吕康银等[1]用Brown分解方法讨论了行业间的性别工资差异；王文静[2]用Granger因果检验分析了行业工资差距的原因；金玉国[3]基于各行业多年份的面板数据,运用协整回归方程分析了我国在计划经济向市场经济过渡的体制转型时期的行业工资差异成因。协整回归分析虽然可以初步研究行业工资与影响因素的关系,且回归参数具有优良的统计性质,但对于厚尾分布数据而言，结论可能失效。而Koenker和Bassett[4]提出分位数回归则能很好地处理样本分布非对称的情况。该方法已被广泛地应用，如陈建宝和段景辉[5]采用分位数回归探讨我国的性别工资差异；陈建宝和丁军军[6]讨论了分位数回归模型的算法及检验；李育安[7]基于分位数回归做了实际应用;蒋翠侠和许启发[8]建立了食品消费支出及其影响因素的分位数回归模型。

在我国劳动力市场上,行业工资差异的严重程度会随着行业垄断程度等影响因素分布位置的不同而不同。此处利用重庆市统计年鉴近14年的数据对农林牧渔业、建筑业、金融业等10个行业做分位数回归分析,研究各行业工资分布的影响因素,以及在不同分位数下各影响因素对行业工资影响的显著性大小和机制。使用的主要研究方法是分位数回归建模方法。

1　行业工资的分布特征

为了样本的同质性,此处研究的样本只包括国民经济中以营利为目的的行业,包括农林牧渔业、工业(采矿业、制造业和电力、热力、燃气及水生产和供应业)、建筑业,交通运输、仓储及邮政业、批发零售业、住宿和餐饮业、金融业、房地产业。选取重庆市2000年至2013年城镇经济单位职工工资,为了对工资进行可行性比较,消除价格因素的影响,以2000年的居民消费价格指数为基期,用各年份的工资除以相应的价格指数。

表1　行业工资描述统计表

注:金指金融业；电指电力、热力、燃气及水的生产供应业；交指交通运输、仓储和邮政业；制指制造业；批指批发零售业；住指住宿和餐饮业；农指农林牧渔业；建指建筑业；采指采矿业；房指房地产业。

数据来源:《重庆市统计年鉴》2000年至2013年相关数据。

表1显示,金融业、电力热力燃气水的生产及供应业的职工工资一直位于前列,而农林牧渔业、住宿和餐饮业的职工工资则普遍较低。从纵向数据看,无论哪个行业工资都呈上升的趋势,说明居民收入水平不断提高。同时,研究的10个行业极值比整体上呈现逐年增大的趋势,在2008年至2010年较为稳定,说明这段时间重庆市各个行业的工资差距没有出现异常值,比较合理。在2011年骤然下降,接着极值比继续变大,行业工资差距拉大。

2　行业工资的影响因素

目前,国外相关文献中对行业工资收入差异的影响因素主要归纳为两种:劳动力市场竞争性因素和非竞争因素。具体包括人力资本因素、劳动负效应因素、工会因素、体制因素等。此处选取垄断程度、劳动生产率和人力资本水平作为影响因素进行分析。其中,垄断化程度以国有企业职工数占行业就业人数的比例表示；劳动生产率等于行业增加值与行业就业数之比；人力资本水平以行业就业数占该年就业总数的比值来衡量。

3　行业工资的影响因素建模分析

分位数回归的思想最早由Koenker和Bassett(1978)提出,是最小二乘估计法的拓展。它依据因变量的条件分位数对自变量X进行回归,得到在不同分位数下的回归方程,可以观察被解释变量在解释变量上的整个分布和它的依赖关系。相比于普通最小二乘法对扰动项零均值同方差不相关的严格要求,分位数回归可以应用于存在严重异方差，或后尾、尖峰的数据,应用的范围更加广泛,挖掘的信息更加丰富。

将年平均工资的对数作为被解释变量y,将垄断化程度、劳动生产率和人力资本水平作为解释变量x,建立如下线性分位数回归模型:

(1)

线性分位数回归模型(1)通过线性规划方法估计回归参数,可以表示为

(2)

式(2)中，ρτ(u)=u(τ-I(u<0))为分段示性函数,满足：

(3)

式(2)显示,分位数回归的模型参数随着τ的变化而变化,并不是一个固定值。此处通过对这3个变量进行分位数回归分析,观察变量的回归参数显著性来判断每个行业关键影响因素的区别。

3.1行业的统计分布特征

与均值回归不同,分位数回归不要求随机扰动项具有方差较小、服从对称分布等特征。当被解释变量散布存在明显的异方差和左偏效应,y的方差随x的增加而上升,均值回归线不仅与0.1，0.9分位数回归线在截距与斜率上都不同,而且与中位数回归线也不重合,此时均值回归已经失效,而分位数回归则具有很好的代表性。此处研究的8个行业的统计分布特征如表2所示。

表2　行业的位置散布特征

数据来源：根据《重庆统计年鉴》2000—2013年的相关数据整理。

表2显示,金融业的分散程度最大,住宿和餐饮业的分散程度最低,自2000年以来该行业的工资分布较为集中；就偏度统计而言,所有行业都服从右偏分布。考虑被解释变量呈现非对称分布并且较为分散,因此采用分位数回归是优于均值回归的。

3.2分位数回归结果

3.2.1工业与金融业

表3显示,两个行业工资收入的均值回归和中位数回归各项参数估计值接近,但仍有区别。特别地，人力资本水平的参数估计值相差偏大,这也说明了在分布不对称时,均值回归直线和中位数回归直线并不重合,分位数回归能更有效、全面地揭示样本信息。从工业和金融业在不同分位点截距项和解释变量的参数估计变化曲线，可以看出垄断程度、劳动生产率和人力资本水平在不同的行业影响机制和影响程度都是不同的。对工业而言,在0.1分位数到0.4分位数间,垄断程度随着分位数的增加,对行业工资收入的负作用在变大,而对金融业工资收入的负作用在减小。

工业分位数回归在不同分位点下各个变量的系数估计值的比较如图1所示。

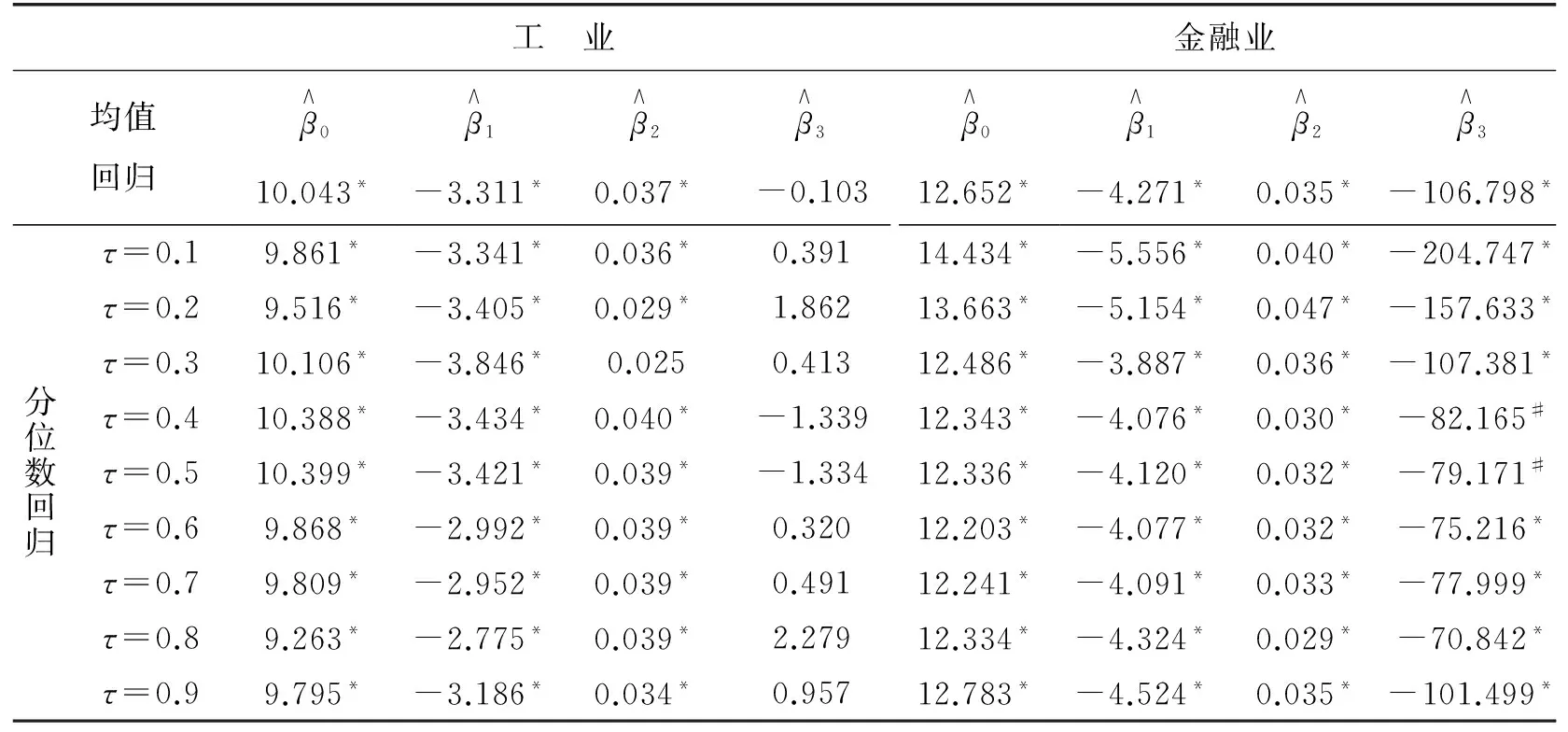
表3　分位数回归系数

注:带*的表示在5%显著水平下显著,带#的表示在10%显著水平下显著,无标记表示未通过显著性检验。

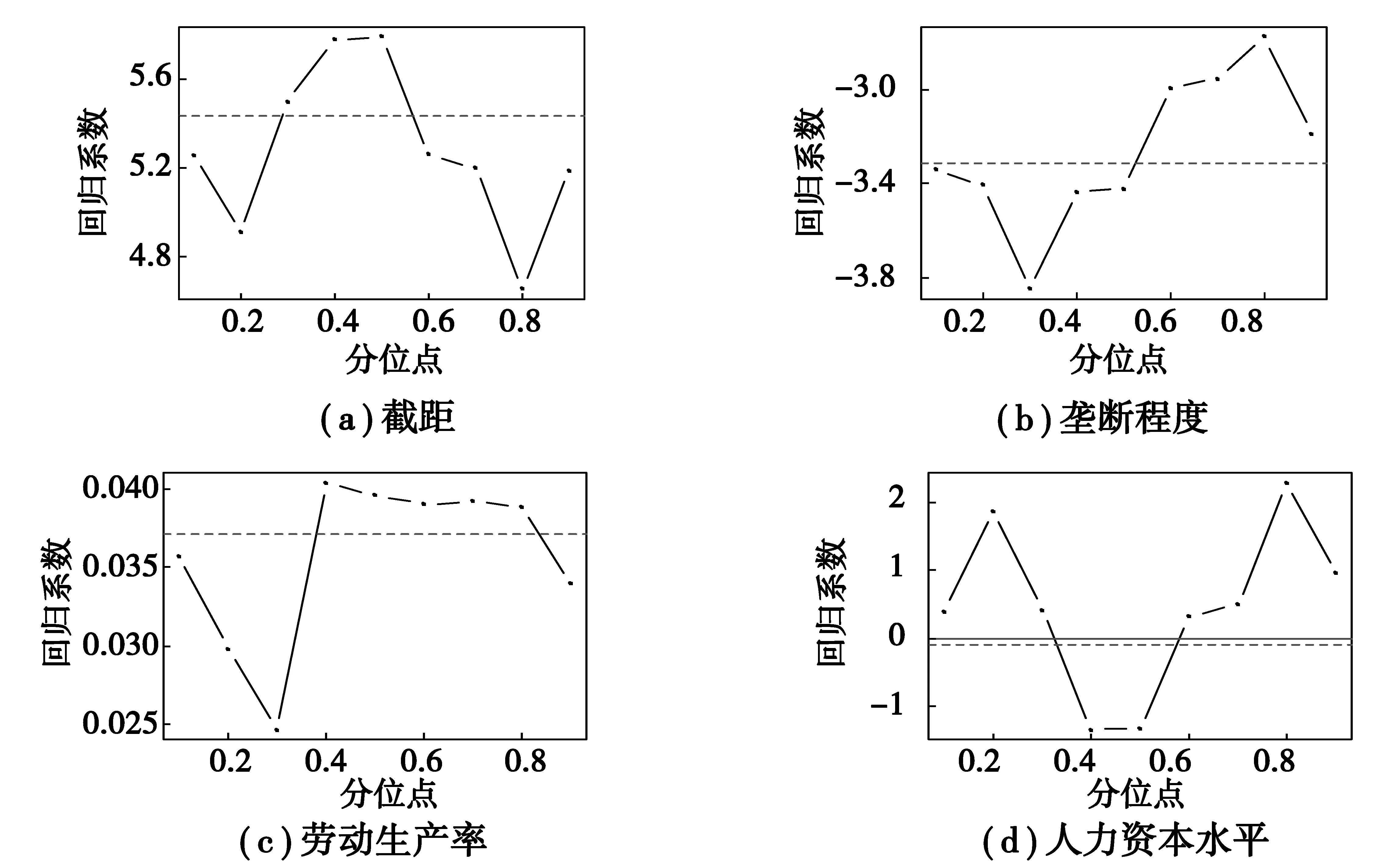
图1　工业各变量的分位数回归系数Fig.1　Quantile regression coefficients of the variables on industry

工业工资收入分位数回归的垄断化程度、劳动生产率在5%显著水平下都通过了显著性检验。人力资本水平的参数估计值在各个分位数下都不显著,说明该行业中人力资本水平的高低对工人的工资收入影响较小。垄断化程度的参数估计值都为负数,反映了行业中垄断化程度越强,对整个行业工作人员的劳动报酬呈负影响效应。同时垄断化程度参数估计值的绝对值随着分位数的增大呈现先增大后减小,最后在0.9分位数上又变大的趋势,表明工业中垄断程度对低分位数上工资收入的影响大于它在高分位数上的作用。劳动生产率是衡量劳动者创造价值的重要尺度,它与工资收入呈正相关,并且劳动生产率在所有分位数上的参数估计值都较为稳定,反映不管是劳动生产率较低或较高,它都与工人的工资密切相关,是影响工资差异的重要因素。

金融业分位数回归在不同分位点下各个变量的系数估计值的比较如图2所示。

金融业工资收入分位数回归的垄断化程度、劳动生产率、人力资本水平绝大部分参数估计值在5%显著水平下显著,只有人力资本水平的参数估计值在τ=0.4,0.5,0.6时在10%显著水平下显著,这表明了垄断化程度等3个因素是影响金融行业工资收入差异的重要因子。其中,垄断化程度的参数估计值的绝对值先变小,再变大,和垄断程度对工业工资的影响刚刚相反,说明垄断程度越强对高分位数的工资影响作用更大。另一方面,垄断程度参数估计值的绝对值远远大于工业,表明垄断程度对金融业的工资差异影响机制更明显。从劳动生产率看,两个行业的参数估计值大小相当,影响程度差不多；另外,人力资本水平的参数估计值均为负数,并且其绝对值在0.9分位数以前随着分位数的变大一直减小,在0.9分位数处较大,一是人力资本水平对金融业工资收入呈负相关,竞争性越大工资收入越低；二是人力资本水平对低分位数上工资收入的影响大于高分位数上的影响。

图2　金融业各变量的分位数回归系数Fig. 2　Quantile regression coefficients of the variables on financial industry

3.2.2农林牧渔业和房地产业

农林牧渔业分位数回归在不同分位点下各个变量的系数估计值的比较如图3所示。

图3　农林牧渔业各变量回归系数结果曲线Fig.3　Quantile regression coefficients of the variables on agriculture,forestry, animal husbandry and fishery industry

农林牧渔业的分位数回归中,垄断化程度、人力资本水平的参数估计值在5%显著水平下都是显著的,而劳动生产率在所有分位点上几乎都不显著,说明劳动生产率这一因素对农林牧渔业的工资收入影响甚微。具体地讲,垄断程度和人力资本水平对该行业的劳动报酬起负相关作用。其中,在0.1分位点处,垄断程度对农林牧渔业的边际效应达到了516.367,随着分位数的增加,参数绝对值在减小,在0.8,0.9分位点处参数由负变正,反映垄断程度对该行业工资的低分位数呈负影响,且边际作用越来越小,对该行业工资的高分位数(0.8以上的)呈正影响,且影响程度较小。人力资本水平的参数估计值随着分位数的变大,影响逐渐变弱,说明该因素对农林牧渔业的低分位数影响力度更大。综上分析,垄断程度和人力资本水平对农林牧渔业工资的高分位数影响较小。

房地产业分位数回归在不同分位点下各个变量的系数估计值的比较如图4所示。

房地产业的分位数回归中,垄断程度的参数估计值在高分位数处通过了显著性检验,低分位处只有当τ=0.1时显著。说明对于房地产而言,垄断程度主要在其工资的高分位数处起显著作用。当τ≥0.5时,分位数越大,显著性越强,边际效应越大。劳动生产率的参数估计值除了在τ等于0.1和0.9时是显著的以外,其余分位点处均不显著,表明劳动生产率对房地产领域内的劳动报酬几乎是不起作用的。此外,人力资本水平的参数估计值均是显著的,并且分位数越高,参数的显著性减弱,边际效应在τ为0.5以前先升后降,在τ为0.5以后(除了τ=0.8)一直下降,整体地说人力资本水平对房地产业的低分位数的影响作用大于其高分位数。

图4　房地产业各变量回归系数结果曲线Fig.4　Quantile regression coefficients of the variables on real estate industry

3.2.3建筑业和交通运输、仓储及邮政业

建筑业分位数回归在不同分位点下各个变量的系数估计值的比较如图5所示。

从建筑业分位数回归中各个变量的回归参数显著性看,劳动生产率和人力资本水平这两个变量在所有分位点处都通过了5%显著水平下的检验,说明这两个因素对建筑业领域的工资收入是显著影响的。而垄断程度只在低分位点τ=0.1，0.2处对建筑业的劳动报酬是显著的,对高分位数的建筑工资报酬而言,垄断程度并不是影响其变化的主要因素。同时,劳动生产率在0.5分位数以前的低分位数处对工资的影响程度小于高分位数处的影响。同样地,人力资本水平在不同的分位数中对因变量的影响也在变化,在0.4分位数以前系数估计值几乎没有较大变化,表明它对低分位数的建筑业工资收入影响显著同时边际作用均衡；在0.4分位数以后,随着分位数的变大,系数估计值先缓慢增加接着迅速变大最后又变小,这也反映了人力资本水平在较高分位数处对该行业的工资差异影响较大,但到了一定的峰值后有所降低。

交通运输、仓储及邮政业分位数回归在不同分位点下各个变量的系数估计值的比较如图6所示。

图6　交通运输、仓储及邮政业各变量回归系数结果曲线Fig.6　Quantile regression coefficients of the variables on transportation, storage and postal services

交通运输、仓储及邮政业分位数回归中,与均值回归类似,垄断程度和人力资本水平的参数估计值都不显著,在条件分位数回归方程中可以剔除这两个变量,它们对该行业的工资收入差异影响并不大。而劳动生产率的参数估计值在5%显著性水平下都是显著的,并且随着分位数的变大,值越来越大,从曲线由陡变缓的走势可以判断劳动生产率对该行业的工资差异影响越来越显著。

3.2.4住宿餐饮业和批发零售业

住宿餐饮业分位数回归在不同分位点下各个变量的系数估计值的比较如图7所示。

图7　住宿餐饮业各变量回归系数结果曲线Fig.7　Quantile regression coefficients of the variables on accommodation and catering industry

在住宿餐饮业的均值回归中3个变量都是5%水平下的显著变量,拟合优度达到了99.3%。在不同分位数的回归中,除了人力资本水平在τ=0.6,0.7处不显著以外,垄断程度、劳动生产率都通过了显著性检验,说明这3个因素与住宿餐饮业的工资收入变化密切相关。具体地,垄断程度和人力资本水平对分位数的变化较为敏感,垄断程度对低分位数工资的作用大于高分位数,劳动生产率随着分位数的变大其边际效应一直增强,但系数大小波动不大,对高低分位数的影响差别不明显。人力资本水平这一因素在0.2至0.5分位数之间，其曲线呈现一个尖峰,τ=0.3时其边际影响是最大的,接着分位数变大,影响作用减弱并趋于稳定。

批发零售业分位数回归在不同分位点下各个变量的系数估计值的比较如图8所示。

从批发零售业分位数回归结果中,知道垄断程度、劳动生产率和人力资本水平都是因变量的显著变量,该行业工资收入变化与它们高度相关。同时,均值回归中各项系数与中位数回归的对应值非常接近。从变化曲线看,虽然劳动生产率的系数估计值总体上在减小,但其变化的数值很小,在不同分位数处对行业工资的影响基本没有太大的变化。对比住宿餐饮业中垄断程度的参数估计值都是正数,垄断程度对批发零售业的影响是负的,并且在高分位数处其影响作用大于低分位数,垄断化越强,整个行业工资平均工资水平越低。人力资本水平则是对低分位数的行业工资影响更大。

图8　批发零售业各变量回归系数结果曲线Fig.8　Quantile regression coefficients of the variables on wholesale and retail trade

4　结　论

对重庆市2000—2013年8个行业工资数据进行分位数回归分析。从整体上看,垄断程度、劳动生产率和人力资本水平是金融业、建筑业、住宿餐饮业和批发零售业的显著影响因素。其中,人力资本水平在金融业等高工资行业至关重要,是金融业工资的决定性影响因素,它对金融业工资的极低、极高分位数处影响较大。因此，政府除引进人才外,还要大力发展各类高等职业教育,鼓励多渠道办学。对于农林牧渔业、房地产业和住宿餐饮业,垄断程度和人力资本水平都是在行业工资的低分位数中影响更大。劳动生产率对工业、建筑业、交通运输、仓储及邮政业、住宿餐饮业和批发零售业等劳动密集性行业影响较大,对交通运输、仓储及邮政业和住宿餐饮业的工资高分位数上影响较大,这也说明工资的高低会反过来刺激影响因素。

除去房地产业和交通运输、仓储及邮政业,其余无论是高收入或低收入行业,垄断程度均是行业工资的显著影响因素。其中,除住宿餐饮业外,垄断程度都对行业工资的提升起着限制作用,垄断程度越低越有利于工资收入的提高。因此,政府可以通过控制不同行业国有企业与非国有企业的比例,缩小行业间工资差异。对农业除了提升劳动生产率以外,应逐步加大对集体经济等非公经济的支持,而金融、房地产业应逐步放松管制力度,在政府调节的同时,增加市场的调节作用。

[1] 吕康银,王文静,张丽.行业工资的性别差异研究[J].山东社会科学，2010(6):157-160

LU K Y,WANG W J,ZHANG L.Gender Differences in Industry Wage[J].Shandong Social Sciences,2010(6):157-160

[2] 王文静.我国城市内部行业工资差异研究[D].长春：东北师范大学,2008

WANG W J.Our Inner-city Industry Wage Differentials[D].Changchun:Northeast Normal University,2008

[3] 金玉国.行业工资差异的制度诠释[J].统计研究,2005(4):10-15

JIN Y G.Industry Wage Differentials Interpretation System[J].Statistical Research,2005(4):10-15

[4] KOENKER R,BASSETT G W.Regression Quantiles[J].Econometrica,1978,46:33-50

[5] 陈建宝,段景辉.中国性别工资差异的分位数回归分析[J].数量经济技术经济研究,2009(10):87-97

CHEN J B,DUAN J H.China Quantile Regression Analysis of the Gender Wage Gap[J].Number of Technical Econo-mics,2009(10):87-97

[6] 陈建宝,丁军军.分位数回归技术综述[J].统计与信息论坛,2008(3):89-96

CHEN J B,DING J J.Quantile Regression Techniques Summary[J].Statistics & Information Forum,2008(3):89-96

[7] 李育安.分位数回归及应用简介[J].统计与信息论坛,2006(3):35-38

LI Y A.Quantile Regression and Application Profile[J].Statistics & Information Forum,2006(3):35-38

[8] 蒋翠侠,许启发.中国城乡居民食品消费行为的分位数回归分析[J].统计与决策,2013(7):118-122

JIANG C X,XU Q F.Chinese Urban and Rural Residents Quantile Regression Analysis of Food Consumption Beha-vior[J].Statistics and Decision,2013(7):118-122

责任编辑：李翠薇

Quantile Regression Analysis of Industrial Wage Differential—Taking Chongqing as an Example

XU Jie, YANG Yi-ping

(School of Mathematics and Statistics, Chongqing Technology and Business University, Chongqing 400067, China)

This paper firstly investigates the distribution feature of wage data of ten industries such as agriculture, forestry, animal husbandry and architectural industry and so on of Chongqing during 2000-2013, then analyzes industrial wage differential status of Chongqing by using the modeling methods such as mean regression and quantile regression respectively in order to find the key factors affecting industrial wage differential and their contributing size to industrial wage differential under the impact of different quantiles and advances the related policies and suggestions for solving industrial wage differential of Chongqing.

quantile regression; mean regression; industrial wage differential; significance

10.16055/j.issn.1672-058X.2016.0005.008

2016-03-16；

2016-05-12.

国家自然科学基金资助项目(11301569)；重庆市基础与前沿研究计划项目(CSTC2015JCYJA00023)；重庆市教委科学技术研究项目(KJ1500614).

徐洁(1990-)，女，四川达州人，硕士，从事经济统计应用研究.

F224.0

A

1672-058X(2016)05-0036-10