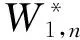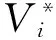带有反馈、启动期、休假中断的多级适应性休假M/M/1排队*
朱少成,刘力维
(南京理工大学 理学院, 南京 210094)
带有反馈、启动期、休假中断的多级适应性休假M/M/1排队*
朱少成,刘力维
(南京理工大学 理学院, 南京 210094)
研究带有Bernoulli反馈、启动期、休假中断的多级适应性休假M/M/1排队系统,结合模型的平衡方程,采用生成函数的方法求出系统中顾客数的概率母函数(PGF)、平均顾客数、系统服务员处在忙期的概率、服务员处在假期的概率、服务员处在启动期的概率以及服务员处在空闲的概率;同时利用强马尔可夫的性质,求出系统中顾客逗留时间的拉普拉斯变换(LST)。
反馈;启动期;多级适应性休假;强马尔可夫性;逗留时间
带有反馈的排队系统在生产和实际生活中有很重要的意义。反馈服务使得经典排队系统的服务机制有所变化,顾客到达系统后并不一定经过一次服务就离开系统,可能会经历多次服务,这个服务次数是由反馈机制所决定的。带有反馈服务排队系统的研究为实际工作中遇到的具体模型提供了一种有利的数学工具。这样的实际模型[1-2]有很多,其中Bernoulli反馈已经被广泛应用于计算机分时操作系统和无线电通讯网络系统中,通过对它的一些指标的研究,研究人员可安排最合理的方案。
在排队系统中,第一个到达的顾客无法立即得到服务,需要经历随机长度的启动时间。徐秀丽[3]给出了稳态队长和等待时间的随机分解;马占友[4]给出了稳态队长的母函数、等待时间分布的LST及其随机分解结果,并推导出忙期、假期和启动期的LST。
过去的几十年里,经典的休假排队系统得到了广泛的研究。1975年, Levy与Yechial[5]引入“休假”和“休假策略”的概念并研究了M/G/1休假排队系统。休假排队反映了在服务结束后,服务员会经历某种机制进行休假,休假模型为各种系统的优化和运行提供了极大的便利。
带有Bernoulli反馈、启动期的M/M/1排队模型有很好的性质,此处结合实际情况,考虑了带有多级适应性休假的此类模型。多级适应性休假与休假中断相结使得这类M/M/1排队系统模型具有更广泛的理论价值和实际意义。
1 模型描述
考虑一个带有Bernoulli反馈、启动期、休假中断的多级适应性休假M/M/1排队系统,顾客按泊松流到达,参数为λ。服务员按照先到先服务的原则为顾客进行服务,服务时间服从参数为μ的指数分布。每个顾客完成服务以后,以概率p(0 g0=F1 令N(t)表示t时刻系统中的顾客数,I(t)表示t时刻服务员所处的状态,则上述排队系统可由马尔可夫过程{(I(t),N(t)),t>0}描述。 在稳态条件λ<μp成立的条件下,给出如下平衡方程: (3) (4) (5) (6) (7) 正则化条件为 为了获得稳态概率,定义如下部分母函数: 则正则化条件可表示为 式(2)两边同乘以zn,并把n从2到∞求和,可得: (8) 式(1)两边同时乘以z并与式(8)相加可得: (9) 式(4)两边同乘以zn,并把n从2到∞求和,可得: (10) 式(3)两边同时乘以z并与式(10)相加可得: (11) 由式(7)得: (12) (13) 由式(5)(6)(7)和式(12)可得: (14) 将式(11)代入式(9),可得: (15) 当式(15)中z=1时,左边为0,右边为 (16) 式(16)引用了式(3)。 对G1(z)在z=1处取极限,通过洛必达法则可得: (17) 将式(12)和式(14)代入式(16)得: (18) 由式(16)(18)和式(11)得: (19) 把式(18)(19)代入式(9)可得: (20) 令式(19)(20)中的z→1,可得: (21) (22) 将式(13)(14)(21)和式(22)代入到正则化条件可得: 通过计算求得: (23) 定理1系统中顾客数的PGF为 (24) 将式(13)(14)(19)(20)和式(23)代入式(24),即可得答案。 令L表示系统中的顾客数,则 令Pw表示服务员处于忙期的概率,则 令Ps表示服务员处于启动期的概率,则 令Pv表示服务员处于假期的概率,则 最后,令Pidle表示服务员空闲状态的概率,则 考虑一个标记顾客,为系统中第n+1个顾客,在标记顾客到达系统之时,系统中已经有n个顾客。标记顾客从进入系统到离开系统的这段时间称作他/她的逗留时间。令W为任意一个顾客的逗留时间,W*(s)为相应的LST。 定理2系统中任意顾客的逗留时间的LST为 证明标记顾客到达系统时,服务员的状态可分为4种情况,即服务状态、启动期、空闲状态和休假状态。 n≥1 (25) n≥2 (26) (27) (28) 针对第一种情况中的(1,1)状态,当前一位顾客服务结束并离开系统时,除标记顾客外,系统中没有人。此时会出现(1,0)状态,与启动期到达的情况不同,这里服务员将立即开始为标记顾客服务,因此有: (29) 针对第三种情况(i,0),i≥1状态,当标记顾客到达系统时,此前系统中没有人。标记顾客到达导致休假中断,服务员立即进入启动期,此时会出现(2,0)状态,因此有: (30) 求解式(25)—(30),可得: (31) (32) (33) (34) (35) 因此,系统中任意顾客逗留时间的LST为 (36) 将式(31)—(35)代入式(36),定理2得证。 系统中任意顾客的平均逗留时间即为 [1] REGE K.On the M/G/1 Queue with Bernoulli Feedback[J].Operations Research Letters,1993,14(3):163-170[2] KUMAR B K,ARIVUDAINAMBI D,WKRISHNAMOORTHY A.Some Results on a Generalized M/G/1 Feedback Queue with Negative Customers[J].Annals of Operations Research,2006,143(1):277-296 [3] 徐秀丽,田乃硕.带关闭和启动期的GI/M/1排队应用[J].运筹管理,2002,11(5):10-13 XU X L,TIAN N SH.With Shutdown and Startup Phase of GI/M/1 Queue Applications[J].Operation Management,2002,11(5):10-13 [4] 马占友,陈利,田乃硕.多重休假的带启动期的M/G/1排队[J].燕山大学学报,2003,27(2):175-177 MA ZH Y,CHEN L,TIAN N SH.On the M/G/1 Queue with Multivacation and Startup[J].Journal of Yanshan University,2003,27(2):175-177 [5] LEVY Y,YECHIALI U.Utilization of Idle Time in an M/G/1 Queueing System[J].Management Science,1975,22:202-211 责任编辑:李翠薇 M/M/1 Queue with Feedback, Start-up, Vacation Interruption of Multi-stage Adaptive Vacation ZHU Shao-cheng, LIU Li-wei (School of Science, Nanjing University of Science and Technology, Nanjing 210094, China) This paper studies M/M/1 queuing system with Bernoulli feedback, start-up, vacation interruption of multi-stage adaptive vacation, by combining with the equilibrium equation of the model, uses generating function to solve the probability generating function (PGF) of the expected number of customers in the system, average number of customers, the probability of system waiter in a busy period, the probability of a waiter in a holiday, the probability of an attendant at start-up stage, and the probability of an attendant in the free period. In addition, by using the properties of strong Markov, the Laplace transform of the customers sojourn in the system is solved. feedback; start-up; multi-stage adaptive vacation; property of strong Markov; sojourn 10.16055/j.issn.1672-058X.2016.0005.001 2016-04-08; 2016-05-10. 国家自然科学基金(11471160). 朱少成(1991-),男,江苏南通人,硕士研究生,从事排队论研究. O226 A 1672-058X(2016)05-0001-05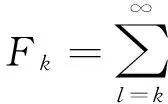
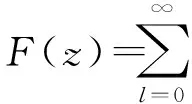
2 稳态分布和系统队长


3 性能指标分析
4 稳态逗留时间的拉普拉斯变换