无线传感网络中不确定数据空值的有效处理

金宗安，杨路明，谢　东

(1.六安职业技术学院 信息与电子工程学院，安徽 六安 237158;2.中南大学 信息科学与工程学院, 湖南 长沙 410083)



无线传感网络中不确定数据空值的有效处理

金宗安1,2，杨路明2，谢东2

(1.六安职业技术学院 信息与电子工程学院，安徽 六安 237158;2.中南大学 信息科学与工程学院, 湖南 长沙 410083)

为了有效的解决无线传感网络中的空值问题，把数据库中的元组分为不相容元组和相互独立元组，给出了两种元组在并操作时的概率计算方法；提出了基于最近邻的加权表决算法PKNN，把存在空值的节点周围k个值经加权计算得到空值的填充值.实验表明，PKNN算法具有较好的准确性和平均绝对误差率，且随着k值的增大，平均绝对误差率不断减小，从而降低了数据的不确定性.

不确定数据；空值；最近邻居

在无线传感网络中，空值的出现有许多种情况：①由于无线数据的传输受到周围温度、湿度等各方面的影响，会出现大量数据的丢失现象(未知值).②由于无线传感网络的数据传输能力限制，网络中的通信线路会因为某种原因而出现断接时，传感器中的数据不能及时传输而丢失，从而使用用户得到一些空缺的值[1].③无线传输节点的能量是有限的，当节点的能量比较低时，此时节点处理不稳定的条件下，有可能不能把有效的数据传输出去(空值或错误的值).

基于信息粒度空值处理也得到了较好的研究，在MC(Mean Completer)算法[2]中，把所有的元组的平均值作为空值的补充值，这种方法没有考虑其它属性的权值，没有较好的理论依据，因此不能作为无线传感网络中空值的处理方法.

CMC(conditional Mean Completer)算法[3]考虑了其它取了出现频率最高的值作为空值的补充值，但没有考虑不同属性之间的相互影响，这对于无线传感网络中数据之间相互关联不相符，因此也不能作为无线传感网络中空值的处理方法.

CC算法(Combinatorial Completer)算法[4]从属性约简属性中选择一个最佳的值作为空值的补充，这种方法能得到较好的约简效果，但当数据中存在较多的空值或数据量很大时，计算的时间代价就会很大.

为了有效的解决无线传感网络中存在相互关联的数据计算并操作的概率，本文把不确定数据分为不相容元组和相互独立元组，并给出了不同的计算方法.针对存在的空值问题，本文提出了基于最近邻居的加权表决计算方法PKNN，把存在空值的节点周围k个值经加权计算得到空值的填充值，算法具有较好的准确性和平均绝对误差率，随着k值的增大，平均绝对误差率不断减小，从且降低了数据的不确定性.

1　问题定义

当在不确定关系中出现空值时，这些空值的处理是比较复杂的，而如果不对这些空值进行处理，则对不确定数据进行查询等操作时，会产生更多不可确定性的结果.如表1所示，对于表1中不确定关系R，假设属性A为确定性属性，属性B和属性C为不确定性属性，取值有不可确定性，ps为确定属性A在不确定属性(B，C)某一取值时的概率，当B，C取值中出现*时代表空值.

由表1中可以看出，当A属性取值为a1时，(B，C)属性取值为(b1,*)的概率为0.65，也就是说B属性取值为b1，而C属性此时取值不确定.

在传统的不确定关系空值处理方法中，目前主要有两种主要的方法，一种是直接把这包含不确定信息进行清除，但随着不确定数据中空值出现的日益广泛，对于这些数据的清除会直接影响整个不确定数据库中数据的完整性.对于表1中，若把含不确定数据时行清除，则表中的确定性属性取值为a2的元组将不再出现，表中的数据如表2所示.当不确定数据中空值出现规模较大时，这种方法是无效的.

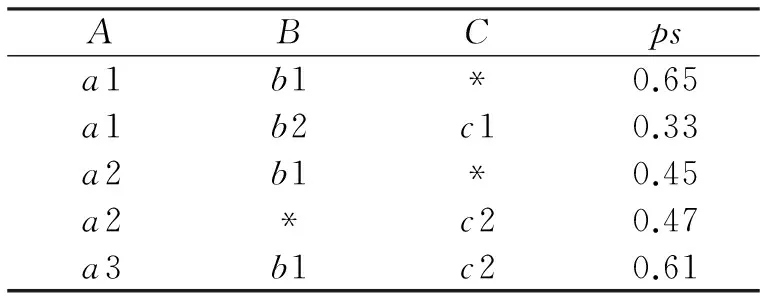
表1　不确定关系R

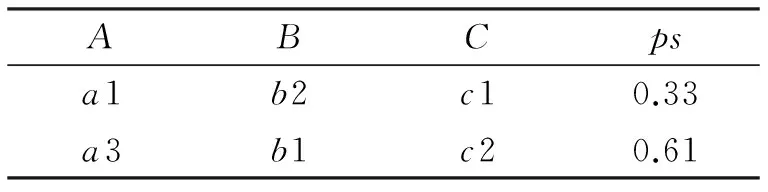
表2　清除空值后的不确定关系

另外一种方法就是当几个互不相依赖的不确定属性出现在同一个不确定关系中，可以通过把这几个互不依赖的不确定关系进行分解[5].例如，表1中的关系，B,C两个互不依赖属性，即一个属性的取值会不会依赖于另一个属性的取值，可以把这种含有空值的不确定关系分解成多个没有空值的不确定关系，但每一种关系中都包含概率属性.把表1中的不确定关系模式分解为表3、表4、表5中的3个关系{A,ps, {A,B,ps}, {A,C,ps}, {A,B,C,ps}.在分解后的不确定关系中，不再含有空值，而原不确定关系中的值都保留在了分解后的不确定关系中.

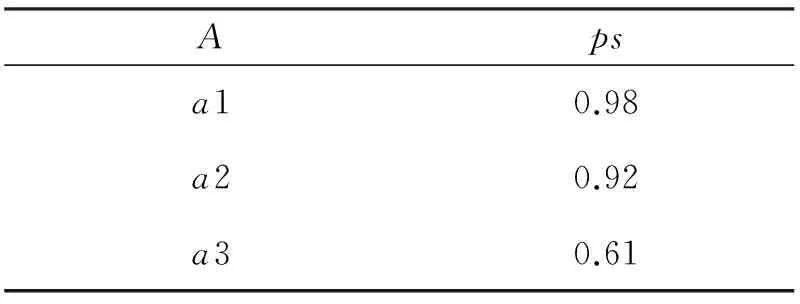
表3　分解后的不确定关系(1)

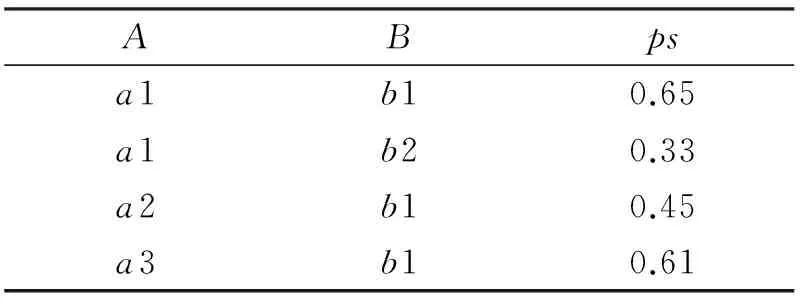
表4　分解后的不确定关系(2)

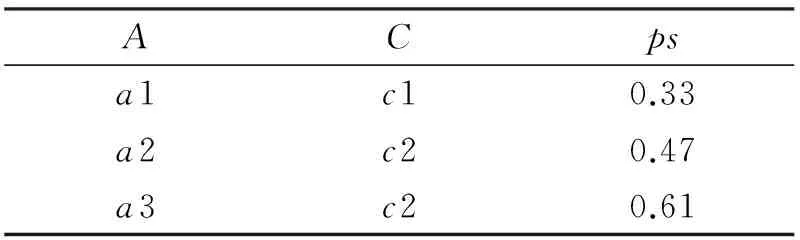
表5　分解后的不确定关系(3)

从表面上看，这样处理方式是可行的，但仔细分析可以看出，分解后的三个不确定关系并不等价于原不确定关系，例如，元组在原不确定关系中的概率是0.33，而在分解后的关系中，却无从得知.因此，在不确定关系中，不能使用分解的方法来消除空值.

而在原不确定关系中，进行代数运算时，采用传统的计算方法，计算的结果不符合实际的要求.例如，对于表1中不确定关系R分别在B属性和C属性上进行投影运算，按照传统的计算方法，计算的公式为

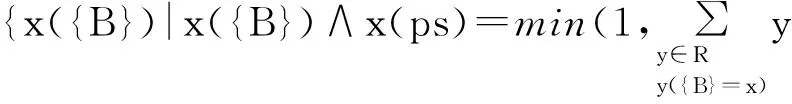
从表中可以看出，B属性取值为b1的元组有三个,,，则b1出现的概率ps为

min{1,0.65+0.64+0.61}=1 .

经计算，整个表的投影运算计算结果如表6、表7所示：

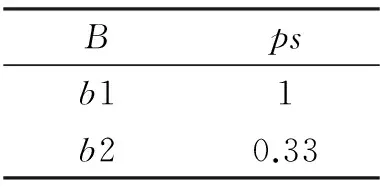
表6　Π{B}(R)计算结果

表7　Π{Ⅰ}(R)计算结果

从上两个表中可以看出，属性B取值为b1是一定出现的，从表7可以看出，属性C取值为c2是一定出现的，它们的概率都为1.而从原不确定关系中可以看出，不确定关系为空的概率为

(1-0.65-0.33)*(1-0.45-0.47)*(1-0.61)=0.000 624.

虽然这个概率很小，但代表属性B取值为b1并不一定出现，所以原概率计算出现了错误.

2　空缺概率的分配

定义1不相容元组(Disjoint Tuple)：在不确定关系R中，若两个元组x,y的确定性属性取值相同，并且它们的取值的概率之和小于等于1，即ps(x)+ps(y)≤1，则把这两个具有相同确定属性取值的元组称为不相容的元组.对于这两个不确定元组x,y，根据不相容事件的概率计算方法，它们的并操作可表示为

p(x∨y)=p(x)+p(y)，

其中，p(x)代表元组x的概率.

例如，在表1中不确定关系R中，元组〈a1,b1,*,0.65〉和〈a1,b2,c1,0.33〉在确定性属性A取值是相同的，都为a1，则这两个元组是不相容的元组.它们并操作的概率为0.65+0.33=0.98.

定义2相互独立元组(Independent Tuple)：在不确定关系R中，若两个元组x,y的确定性属性取值不相同，则把这两个元组x,y称之为相互独立元组.根据相互独立事件的概率计算方法，它们的并操作可表示为

p(x∨y)=1-(1-p(x))(1-p(y)).

例如，在表1中不确定关系R中，元组〈a1,b1,*,0.65〉和〈a3,b1,c2,0.61〉在确定性属性A取值是不相同的，则这两个元组是相互独立元组.它们并操作的概率为1-(1-0.65)*(1-0.61)=0.136 5.

定义3最近邻居(Nearest Neighbor)[6]：在n维空间里，对于查询q，在一个设定的查询对象集合S中，找到与查询样例q的属性相对接近的子集NNS(q)，这个子集满足如下公式成立：

NNS(q)={r∈S|∀p∈S,dist(q,r)≤dist(p,p)}.

也就是说，在S的子集r中的数据点距离查询点q的之间距离要小于或等于同样S子集的p中的点和q的距离，此时r中的点即是q的最近邻居.

如果r中元素的个数为l时，就是单个的最近邻居查询，如果r中元素的个数大于1时，比方说为k，此时q的k个最近邻居，dist表示两对象间的最小距离，dist(q,r)表示q，r两点的距离.

定义4相异度(Dissimilarity)，由欧几里德距离定义，其中两个点X(x1,x2,...,xn)和Y(y1,y2,...,yn)的欧几里德距离如公式(1)所示：

(1)

其中n是维数，xi和yi分别是x和y的第i个属性.对于两个标称属性描述的对象，如果它们的属性值不匹配，则说明它们的相异度为1，如果匹配则说明它们的相异为0.

在多数表决方法中，每个近邻对分类的影响都一样，这使得算法对k的选择很敏感.降低k的影响的一种途径就是根据每个最近邻xi的距离不同对其作用加权：wi=1/D(x′,xi).结果使得远离x的训练样例对分类的影响要比那些靠近x的训练样例弱一些.使用距离加权表决方案，类标号可以由公式(2)确定,距离加权表决：

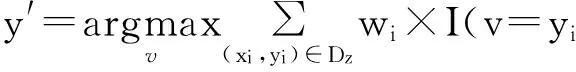
(2)

上述公式中，v是类标号，yi是一个最近邻的类标号，I(.)是指示函数，如果其参数为真，则返回1，否则，则返回0.

3　算法设计

使用基于最近领居分类方法存储无线传感网络中不确定数据，当有新的不确定数据出现时，要构建新的构造模型，对数据进行分类.k最近邻居分类的每一个数据对象一般有N个数据属性，可以把N个数据属性构成N维空间模式进行存储，每一个N维空间代表一个数据对象.使用k最近邻居分类算法搜索存储的数据，计算最近的k个数据对象作为k最近邻居.

算法1 搜索传感节点k个近邻的算法：PKNN(A[n],k) .

输入：A[n]为N个传感节点样本在空间中的坐标，k为节点x最近邻数，含有空值的不确定数据

输出：填补空值后的不确定数据

取A[1]～A[k]作为x的初始近邻，计算与测试样本x间的欧式距离d(x,A[i]),i=1,2,.....,k；按d(x，A[i])升序排序，计算最远传感节点与x间的距离D=max{d(x,a[j]) | j=1,2,.....,k};

for(i=k+1;i<=n;i++)

{

计算a[i]与x间的距离d(x,A[i]);

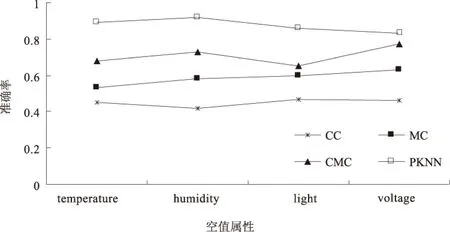
if(d(x,A[i]))

then 用A[i]代替最远节点

按照d(x,A[i])升序排序，计算最远节点与x间的距离D=max{d(x,A[j]) |j=1,...,i};

End

}

计算样本集合A[i],(i=1,2,...,k)的概率并记录它们所属的类标号，依此计算并填充样本x的空值.

本算法通过采集出现空值x的N个周围空间坐标值，先计算与已知样本x前k个测试样本距离，这k个点的最远欧式距离设为D；然后依次计算剩余测试样本数据集合中所有数据与样本x间的欧式距离dist，当dist小于D时，则把此测试样本存储到k-最近邻中，直到所有的测试样本都计算完，并按类标号的频率依次排序，把频率最大的类标号作为空值计算的依据.

如果选择合适的k值要结合实际运用的情况，当k值较大时，距离某一个点的较远点中的数据也会出现在最近邻居列表中，这样有可能出现错误的分类测试样例.如果选用的k值较小时，距离某一个点的较近的一些数据会排出在最近邻居列表中.因此，选持合适的k值是也是实际应用要考虑的一个重要问题.

4　实验分析

无线传感网络不确定数据空值处理的实验环境为Windows 7系统，Intel(R) Core(TM) i5-4200M CPU,主频2.50 Ghz，内存3 GB，SQL Server2008数据库.不确定数据空值处理采用C++编程实现，实验采用了Intel Berkeley Research Lab实验室提供尺寸s=143 MB的数据，这些数据由54个传感器每31秒收集一次，每个数据有4个属性(temperature、humidity、light、voltage).

采用rand()函数对实验数据集进行处理，产生随机的空值.对于数据样本数为n的m维数据集R，随机产生x个空值，其过程如下：

Fori=1 tox

H=int(n*rand())+1

L=int(m*rand())+1

R(H,L)=NULL

Next

针对Intel Berkeley Research Lab数据集的四个属性分别使用CC、MC、CMC和PKNN算法进行验证，如图1所示.从图1中可以看出，CC算法虽然使用约简属性中最好的一个作为补充，但效果确最差，因为这种算法并不适用于无线传感网络中的数据；MC算法使用平均值填充，没有考虑决策属性，而CMC虽然考虑了决策属性，但并没有考虑无线传感网络中数据的不确定性，因此它们的确准率并不是最好；PKNN算法综合考虑无线传感网络中数据和节点之间关联的特点，采用基于距离的加权表决，根据数据的不确定性的大小和距离的远近计算空值的填充值，因此其准确率明显高于其它算法.

图1　填充准确率对比

由于空值的计算采用的是基于近邻居的加权距离表决，因此，近邻数对各算法的平均绝对误差有不同影响，如图2所示.从图2中可以看出， 当k值较小时，算法的总体平均绝对误差率较大，随着k值的增大，算法的平均绝对误差在减小，

图2　k值对平均绝对误差率的影响

5　结语

本文针对无线传感网络中不确定数据空值进行了有效的处理，针对不相容元组和相互独立元组给出了不同的并操作计算方法，提出了基于最邻居的加权表决计算方法PKNN，算法具有较好的准确性和平均绝对误差率.但无线传感网络中不确定数据很问题都还没有效解决[7]，以后主要研究方向为①不确定关系数据库中自连接查询的处理：当一个关系的名称在一个查询中出现两次的时候，如何判断它是一个线性的还是NP难的查询；②查询优化：不确定关系数据库的查询优化和确定性的数据库的查询优化有些类似，但也不同的地方，如何更好的对不确定关系数据库进行优化仍然是一个问题.

[1]Ye M, Lee W C, Lee D L, et al. Distributed processing of probabilistic top-k queries in wireless sensor networks[J]. IEEE Transactions on Knowledge and Data Engineering, 2013,25(1):76-91.

[2]姜延吉，黄凤岗．存在型空值插补的特征约简方法研究[J]．哈尔滨工程大学学报，2010，31(6):743-748．

[3]李聪，梁昌勇，杨善林．基于粗糙集的不完备信息系统空值估算方法[J]．计算机集成制造系统，2009，15(3):604-608．

[4]张霞，储尚军，许鸣珠．基于粗糙集的不完备信息系统空值补齐算法[J]．小型微型计算机系统，2011，32(4):752-756．

[5]Olteanu D, Huang J, Koch C. Approximate confidence computation in probabilistic databases[C]Los Angeles:Proceeding of the 29th ICDE Comference,IEEE press, 2010.

[6]Cheema M A, Lin X M, Wang W, et al. Probabilistic reverse nearest neighbor queries on uncertain data[J]. IEEE Transactions on Knowledge and Data Engineering，2010, 22(4):550-564.

[7]Dalvi N, Suciu D. Efficient query evaluation on probabilistic databases[J]. International Journal on VLDB, 2006,16(4):523-544.

责任编辑：赵秋宇

Efficient Processing of Null Value on Probabilistic Data in Wireless Sensor Network

JIN Zong-an1,2，YANG Lu-ming2，XIE Dong2

(1.SchoolofInformationandElectronicEngineering,Liu’AnVocationTechnologyCollege,Liu’an, 237158China;2SchoolofInformationScienceandEngineering,CentralSouthUniversity,Changsha410083,China)

In order to effectively solve the problem of empty value in wireless sensor networks, the paper presents a method for calculating operation probability of different tuples in the database. In which the tuples are divided into dependent tuples and independent tuples. In this paper, we propose a weighted algorithm PKNN, which is based on the nearest neighbor, to calculate the filling value of the null values by the weighted values of the k nodes around null values. Experimental results show that the proposed PKNN algorithm has a better accuracy and lower average absolute error rate. With increase of k, the average absolute error rate decreases. Thus, it can effectively reduce the uncertainty of the data.

probabilistic database; null value; nearest neighbor

2016-01-22

安徽省优秀青年人才基金重点项目(2013SQRL143ZD)

金宗安(1983—)，男，河南信阳人，讲师，硕士，研究方向：不确定数据处理．

1671-9824(2016)05-0055-06

TP311

A