永磁同步直线电机端部效应的分析及结构优化

李耀辉

(许昌学院 电气工程学院，河南 许昌 461000)



永磁同步直线电机端部效应的分析及结构优化

李耀辉

(许昌学院 电气工程学院，河南 许昌 461000)

根据麦克斯韦理论，对永磁同步直线电机磁场的端部效应进行有限元建模、仿真和分析，并在此基础上对单电机和基于相叠加原理的多电机移结构进行优化，从而设计了圆筒型直线电机，并与排推动型直线电机的端部效应进行比较，说明优化后的结构模型对更好地改善了端部效应.

永磁同步直线电机；端部效应；有限元分析；结构优化

Maxwll所建立的电磁理论体系是研究电磁场理论的前提与基础，主要包括高斯定律、安培环路定律和法拉第定律.包含初级电枢绕组、次级永磁体和二者之间气隙的永磁同步直线电机内的一切电磁现象也都可以用经典的麦克斯韦电磁学理论来描述.为此，进行该直线电机端部效应的建模及有限元分析，并对电机结构进行优化来改善端部效应.

1　端部效应的有限元分析及仿真

1.1端部效应的建模

永磁同步直线电机磁场分析步骤包括：①依据电机结构、特点及属性建立合理有效的磁场模型；②通过Ansys对所建立的模型进行有限元划分；③依据该电磁模型，设置满足一定要求的电磁载荷和边界条件并对其进行设置，使其满足建模要求；④利用Ansys对所建立的电磁模型进行网格划分，然后对划分好的网格模型进行求解和分析.

本文根据麦克斯韦电磁理论，根据设定好的相关材料及电流源,利用有限单元法求解出磁共能W1，且W1=∫∫∫0.5 BHdv或W1=∫∫∫0.5B2/μdv.然后，计算力的单元移动微距Δs，相同电流下，重新利用有限元法求解新位置磁共能W2，得到所受电磁力为F=(W1-W2)/Δs.利用储能概念计算力和力矩是最为精确和可靠的方法.据此，永磁同步直线电机参数设计如下：(1)初级电枢：电流相数m为3，极数p为6，每相匝数N为240，齿槽数Q为18，齿槽距t为12 mm，齿槽宽t为6 mm，齿槽深ds为30 mm，初级铁芯高a为50 mm，铁芯长度L为222 mm；(2)次级永磁体：极距τ为36 mm，永磁体高度h为3 mm，永磁体宽度w为30 mm；(3)气隙高度g为1 mm，绕组中的电流I和电阻R分别为2 A和5 Ω.

进行有限元建模时，需针对分析要求进行对象的简化(比如对称性).为全面反映直线电机的磁场状态，可建立三维模型.然而，其边界条件复杂且计算量大，如果暂且消除电机端部效应的影响因素，直线电机可变为一个简单的二维模型，如图1所示.

对图1中的分析模型进行手动网格划分，这主要针对绕组区域和永磁体进行的，而图中其他不规则的模型结构可直接利用智能划分方法实现.划分后的网格模型如图2所示.

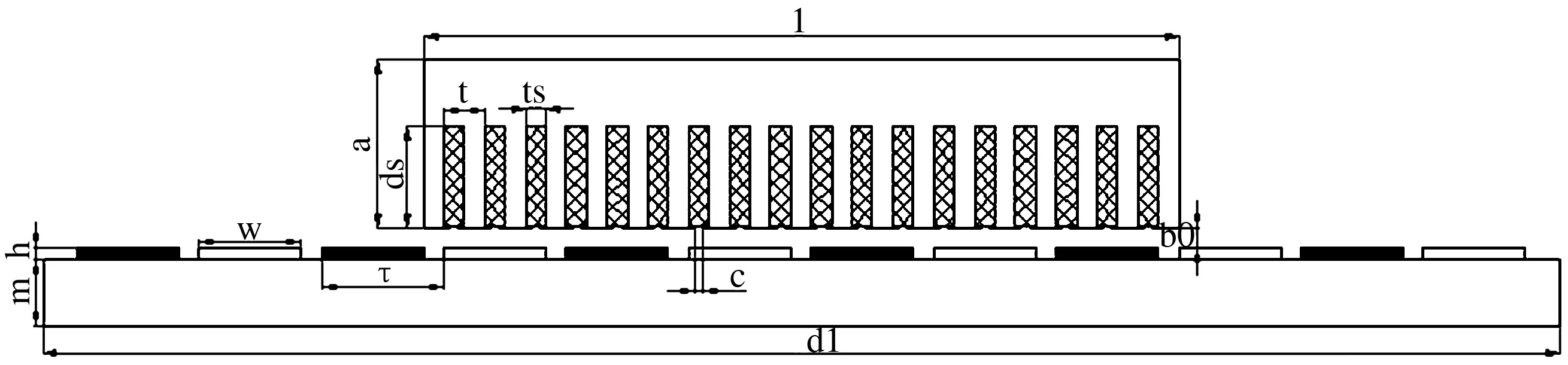
图1　消除电机端部效应影响下直线电机的ANSYS分析模型

1.2端部效应有限元分析

直线电机两侧的开端可造成磁场突变而引起端部波动力[1]，此外，初级动子长度的优化可明显改善其端部力大小.实际模型中，电机初级动子的端面正交于永磁体面，这种正交特性将使磁场分布发生较大的变化.为排除其他效应影响，端部效应建模如下：用光滑电枢实体代替齿槽和绕组，在线圈不通电和单独永磁体磁场作用下，在ANSYS中建立模型得到的磁力线分布如图3所示.明显可以看出，磁力线在端部突变过大.用Maxwell法得到端部力Force-X和法向吸引力Force-Y分别为578 N及50 161 N.

图2　永磁同步直线电机模型的网格划分图

图3　磁场在光滑电枢下的分布情况

根据磁链分析，在动子铁芯长度恒定时，端部力的大小与动子和定子的相对位置有关[2].以2 mm为循环步长，选定动子铁芯长度222 mm，采用APDL命令流循环，得到的端部波动力和法向的吸引力如图4所示.明显地，初级的移动距离在0～2τ(即0～72 mm)这个范围内变化，而其法向力和边端力的变化的趋势是一致的，都是以极距τ(即36 mm)为周期.

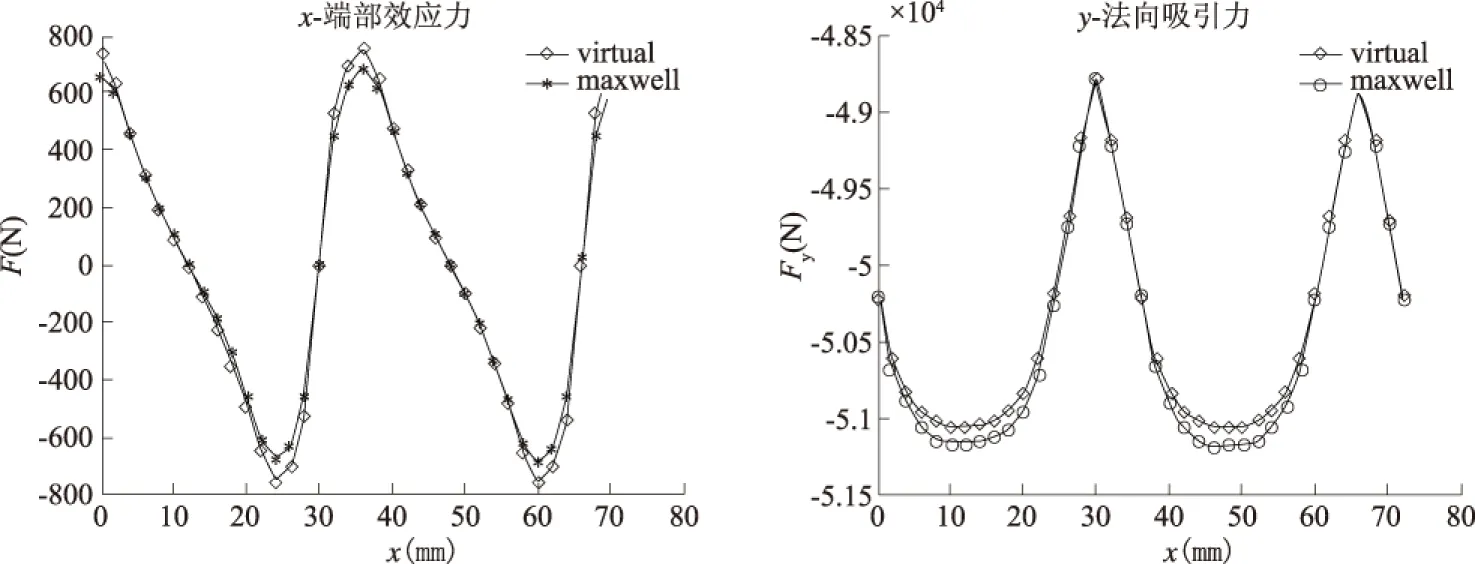
图4　铁心长度为222 mm时，初级在0～2τ范围内端部力和法向力的波动情况

波动力的变化主要受铁芯长度与极距的影响. 首先，可利用铁芯长度的变化来分析端部力的变化情况.选取铁芯长度分别为222 mm、258 mm和294 mm，初始动子移动两个极距后，其与端部效应力都是以极距τ为周期进行波动的.此外，由于初级动子的长度与端部效应力之间存在一定联系，因此，在极距范围内选取的初级动子的长度，并将其不断变化，从而引起边端力的波动，结果如图5所示.

当初始条件相同的情况下，选取铁芯长度在222～258 mm之间，以极距的四分之一为增量，分析得到0～2τ范围内端部力的变化情况，如图6所示.从图中可看出，其波动周期是不一致的，与前面的分析结果基本吻合.此外，不同铁芯长度会导致端部波动力的幅变化比较明显.初步观测，当L取240 mm，其波动幅值最小.

验证这一结果是否正确，选取L为222～294 mm，为了能在较小的计算量下尽可能多的取点，选取增量Δ=3 mm，通过分析得到铁芯长度与端部力幅值之间的函数关系，具体如图7所示.可看出，端部力波动幅值与动子长度以周期τ变化.而且，在L=kτ时，端部力波动的幅值达到最大，在L=(k+1/2)τ时，端部力波动的幅值达到最小.这样的分析结果和波动趋势与理论基本吻合.

当利用不同的电机初级长度时，永磁直线电机将受到法向力的作用[3]，如图8所示.此刻的法向力将以极距τ为周期进行上下波动.其法向吸引力的大小与电机长度成正比.这与边端力的受力情况类似，当L=(k+1/2)τ时，其波动的幅值最小.因此，直线电机的端部效应和法向吸引力波动在L=(k+1/2)τ时最小，这为直线电机的设计优化提供有力依据.

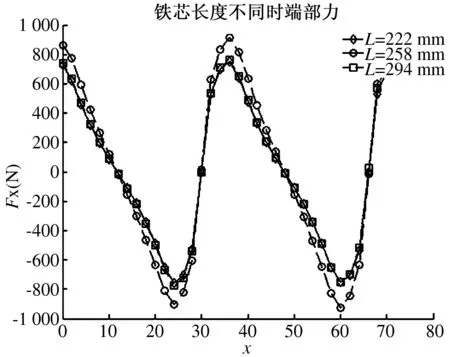
图5　不同铁芯长度下的端部力

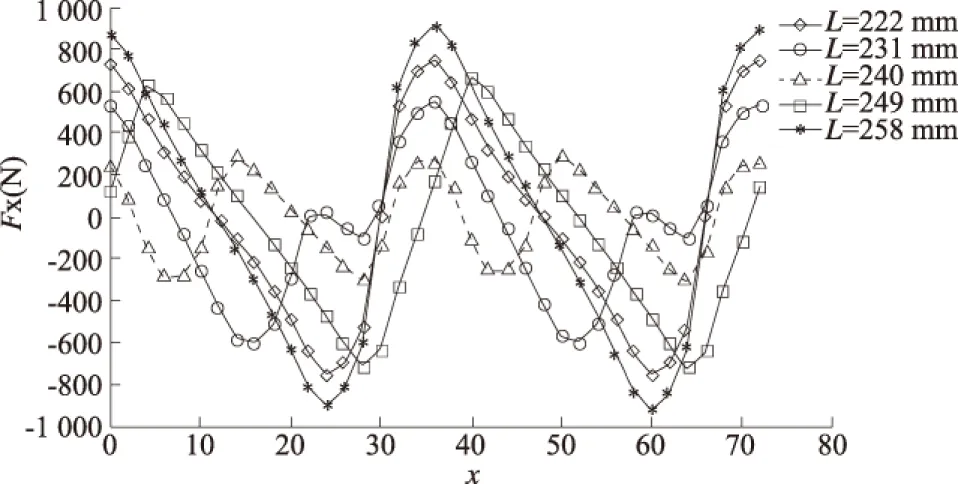
图6　不同初级长度下边端力的大小

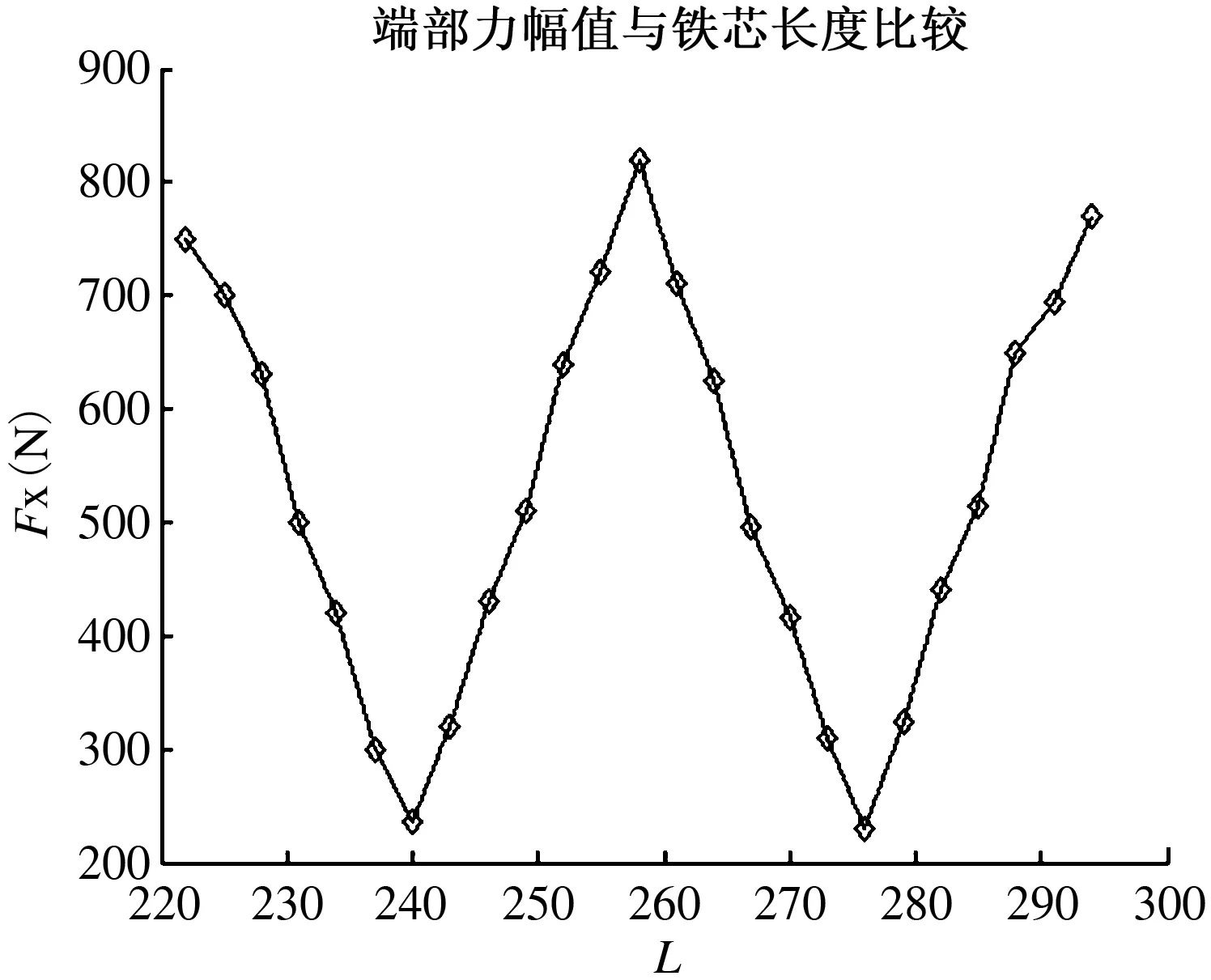
图7　端部力幅值与铁芯长度的函数关系

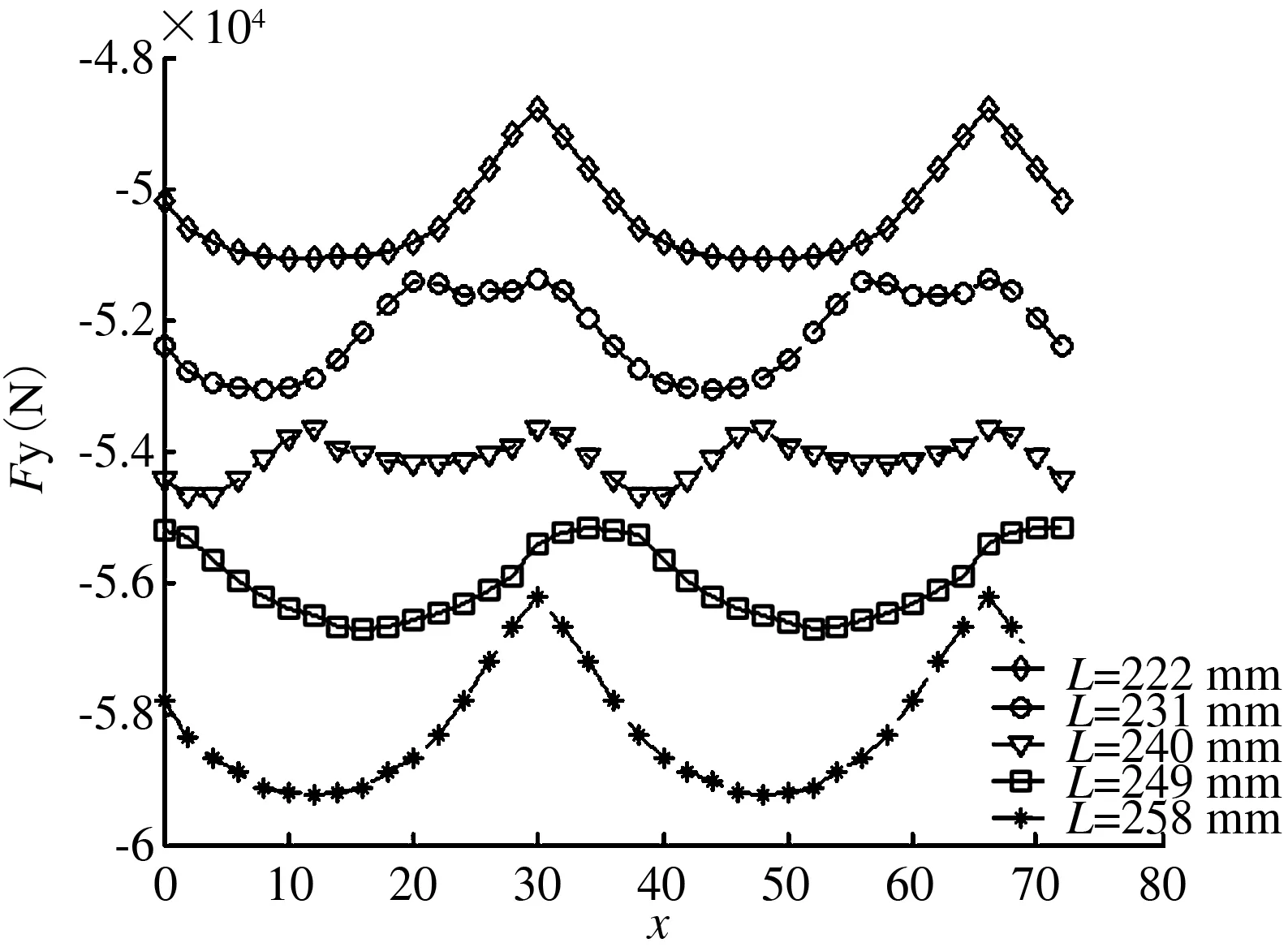
图8　不同初级动子长度下的法向力

2　直线电机结构优化

2.1单电机优化

直线电机端部效应的结构优化是针对两个关键参数进行的.一个是直线电机的长度，另一个是直线电机的边端结构.在电枢进行开断的过程，电机内部的磁场的分布情况将会产生奇异变化，而且这种变化很难完全消除掉.唯一的解决方案就是通过各种各样补偿方法加以减小甚至消除[4].而材料力学中有如何消除机械集中应力的相关方法，这里主要是将初级动子的端部进行相应的平滑处理来减少集中应力.依据此思想所建模型如图9所示，磁力线在端部的突变明显改善.用Maxwell法得到纵向边端力和法向吸引力分别为63.8 N和37 164 N.随着纵向边端力的不断减小，相应的法向吸引力会不断地减小.因此，减小纵向边端力的方法能够在一定程度上减小端部效应.但从机械加工角度讲，圆角将加大加工难度.故采用此种方法时，需要做进一步改进. 可选择电机的长度L=(k+1/2)τ左右.为减小横向边端效应的影响，k的取值不能太小.另外，端部力的分布是以τ为周期的类正弦形式，考虑可采用多初级移相叠加. 值得注意的是，与叠加相比，单台直线电机的优化效果将不会有太大改善.

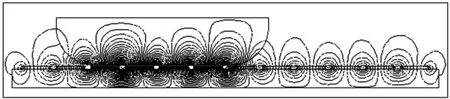
图9　平滑处理后的磁场分布情况

2.2基于多电机移相叠加原理的结构优化

为满足直线电机的平稳传动以及推力性能的要求，可以将多台直线电机并联后进行再驱动[5].而数控机床中的重心并行驱动技术达到良好的驱动效果.有效控制直线电机的精度是相当复杂的，控制成本也会随着精度的提高而快速上升.为满足一定的精度要求，可对直线电机的机构进行改进、改变或优化，从而降低对电机控制系统对其精度要求.由于开断的初级铁芯将产生互不相等的三相绕组互感，从而在三相互感线圈中产生互不对称的感生电流，最终导致直线电机不能正常运行，从而引发磁场出现零序和负序现象.因此，单台电机不能合理有效的工作，这就需要使用多台电机.由于所使用的是三相点，可以同时利用三台功能相同的直线电机的绕组换位来消除电流不对称的现象.其换位方法如图10所示.将第1台永磁直线电机的相A、第2台的相B以及第3台的相C串联为第1相；将第1台永磁直线电机的B相、第2台电机的C相以及第3台电机的A相串联为第2相；剩余的串联为第3相. 这样的接法同时保证了三相负载的对称性，有效消除了三项绕组中电流不对称的现象.

根据前面分析，空载情况下，直线电机端部效应力是以极距τ为周期进行类正弦波动的.因此，对于三台电机，可采用移向三分之一极距(彼此间相差120度)的角度实现叠加，从而有效消除波动.其连接方式如图11所示.且三相对称电流经电机1的A、B和C相通入，对该叠加电机模型进行有限元仿真分析和求解，等到纵向力的分布，如图12所示.图中的m1、m2和m3分别表示光滑电枢下三台直线电机的纵向端部力.每台电机波动的峰值为Fx=507 N，三台叠加后的峰值是Fx=317.5 N，其波动减小了189.5 N(大约减少百分之三十七点四).

图10三台直线电机的Y型连接(a)和△连接(b)图11电机三相绕组的接线图

直线电机不对等的横向结构将产生不封闭的磁场，从而造成横向的边端效应，其理想模型难以产生[6].不过，如果整个磁场处于封闭状态，我们可以忽略这种横向结构所产生的效应影响.解决方法是将排推方式的永磁同步直线电机结构变为圆筒型永磁同步直线电机[7].具体实现步骤如下：(1)首先，将叠片动子均匀地分布到圆周上；(2)将这些叠片按一定顺序关联起来，以便让边缘磁场处于封闭状态.通过这两个步骤，既可以减小直线电机结构的体积，又可以消除横向端部效应的影响.更为重要的是，可避免单一电机下导轨的压力过大所引起的变形以及摩擦阻力增加的问题[8].设计优化的电机本体结构如图13所示，其纵向力分析结果如图14所示.图中‘m1’、‘m2’和‘m3’分别表示光滑电枢下三台直线电机纵向端部力的波动情况，‘sum’表示三台直线电机端部力叠加后的结果.从图14中可明显可以看出波动力并没有得到明显的改善.但是，图14的波动结果并不能说明图13的圆筒型结构没有实际作用.而是该结构与实际建立对象是相吻合的.毕竟，该结构优化了直线电机的齿槽效应，在没有任何负载的条件下，主要的作用力就是齿槽力，图14的结果很好地证实了这一点，即叠加后的齿槽力并没有明显增强，这样的仿真结果与所预期的相吻合.当直线电机处于高速运行状态情况下，齿槽力对直线电机影响相对较小，而电机的端部效应力具有较大影响.

图12　光滑电枢下的纵向力

图13　新结构圆筒直线电机本体结构图

当直线电机处于负载运行状态下，向初级绕组通入电流后，通过仿真分析后所获得的纵向波动力分布如图15所示.图中的‘m1’、‘m2’和‘m3’和‘sum’分别表示纵向端部力的波动情况以及三台直线电机端部力叠加后的结果.利用图13的圆筒型直线电机结构，可以将其推力获得极大的改善.单机叠片情况下的纵向力波动幅值为1 920 N/m，平均值为9.46 N/m，而叠加后的幅值为510 N/m,平均值为0.72 N/m.分析结果说明：在电机结构成本不增加的条件下，圆筒型永磁同步直线电机比平板型永磁同步直线电机具有更加有效且稳定的推力特性，更重要的是，圆筒型电机只需要很小的体积就可实现同样功能.如果加以配备合适的控制系统，就能够得到更精确的伺服效果.

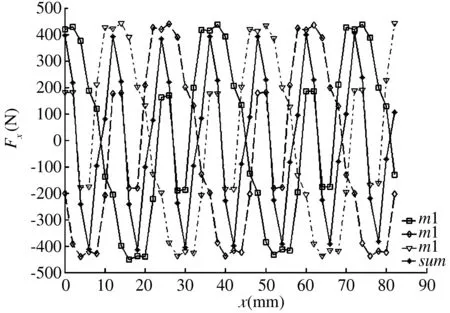
图14　空载下叠片获得的纵向力

图15　负载时在不同初始位置电机的纵向波动力

3　结语

采用有限元分析软件分析了端部效应力对直线电机的推力影响.此外，与经典的旋转电机理论以及永磁同步直线电机的优越性能相结合，对永磁直线电机的结构特征进行了深入分析和改进，并提出针对直线电机的结构优化方案，最后说明了三台电机的叠加是如何抵消纵向动力波动的.

[1]曹江.永磁直线同步伺服电机的端部效应分析[J].科技广场,2011(3):154-156.

[2]王昊,张之敬,刘成颖.永磁直线同步电机纵向端部效应补偿方法[J].中国电机工程学院，2010,30(36):46-52.

[3]沈丽.高精度永磁直线伺服电机法向力波动分析与抑制方法研究[D].沈阳：沈阳工业大学，2014.

[4]杨云涛，石志勇，关贞珍，等.一种基于磁偶极子磁场分布理论的磁场干扰补偿方法[J].兵工学报，2008,29(12):1 485-1 491.

[5]马秀娟，孙洋，张华强，等.基于DTC-SVM的多电机并联驱动系统[J].电机与控制应用，2014,41(6):5-10.

[6]王利.现代直线电机关键控制技术及其应用研究[D].杭州：浙江大学，2012.

[7]寇宝泉，杨国龙，李鹏，等.双向交链横向磁通圆筒型直线永磁同步电机的基础研究[J].中国电机工程学报,2012,32(23):61-67，13.

[8]沈建新,王灿飞,费伟中,等.永磁开关磁链直线电机若干优化设计方法[J].电工技术学报，2013,28(11):1-8.

责任编辑：赵秋宇

Analysis and Structure Optimization on End Effect of Permanent Magnet Synchronous Linear Motor

LI Yao-hui

(CollegeofMechatronicEngineering,XuchangUniversity,Xuchang461000,China)

Based on Maxwell theory, the end effect on the magnetic field of permanent magnet synchronous motor is constructed by finite element method, simulation and analysis. In view of the above results, the structure of the motor is optimized by the single and superposition-principle based motor. A cylindrical linear motor is designed, and the end effect of the cylindrical linear motor is compared with that of the array promoting linear motor,which proves that the structural model of the optimized structure has better improved the end effect.

permanent magnet synchronous linear motor; end effect;finite element analysis; structural optimization

2016-02-12

河南省科技厅基础与前沿资助项目(162300410263);河南省教育厅重点科研项目(14A46023)

李耀辉(1981—)，男，河南许昌人，讲师，博士，研究方向：CAD/CAM，系统建模、仿真与优化等.

1671-9824(2016)05-0044-05

TM341

A