广义正交表相遇平衡性的等价条件

吴亚桢，杨　林，张应山，廖靖宇，田　萍

(1.许昌学院 数学与统计学院，河南 许昌 461000；2.华东师范大学 统计学院，上海 200241)



广义正交表相遇平衡性的等价条件

吴亚桢1，杨林1，张应山2，廖靖宇1，田萍1

(1.许昌学院 数学与统计学院，河南 许昌 461000；2.华东师范大学 统计学院，上海 200241)

广义正交表是一种类似于正交表的新设计,其数据分析保持了正交表的优良性,即,各个因子的估计是无偏估计,并且方差达到最小,但试验次数大幅减少.相遇平衡性是广义正交表的两个平衡条件之一, 也是正交相遇平衡区组设计必须满足的一个基本要求.利用矩阵象技术, 给出了相遇平衡性的一个等价条件, 借助于SAS 软件可以方便快速的进行验证.

正交相遇平衡区组设计；广义正交表；相遇平衡；矩阵象

试验设计的基本问题是要求试验的分析结论具有再现性，即：对于同样的试验问题，不同的试验工作者，无论采取什么样的合理设计来收集数据，根据数据进行数据分析的分析结论应该是唯一的，这种分析结论不但和试验工作者的假设无关，而且和试验工作者的操作行为无关.可以证明：正交表试验和相应的数据分析结论具有这种再现性要求[1,2].广义正交表是在保证试验具有类似于正交表数据分析的基本要求下提出的一种新的设计，这种设计可以和正交表一样用于试验设计和相应的数据分析，也可以证明其数据分析结论是具有再现性的[3-6].

广义正交表要求设计表具有两个最基本的平衡性质：正交平衡和相遇平衡.

正交平衡是指多个试验因子中的各个试验因子的组合配搭之间的一种平衡.这种平衡性是保证对多个试验因子中的各个试验因子之间的处理是公平的，试验工作者无论对于试验因子赋予任何内容，虽然试验的数据分析结论将会随着试验工作者的赋值予以变动，但不会影响各个试验因子的分析结论.如果试验没有正交平衡性的要求，那么对多个试验因子中的各个因子的试验效果比较将会失去公平，也将不能保证试验的再现性要求.因此，正交平衡是进行多个试验因子的试验设计必须考虑的一种平衡要求.

相遇平衡是指每个试验因子的各个试验水平的组合配搭之间的一种平衡.这种平衡性保证试验因子对各个试验水平的处理是公平的，试验工作者无论对于试验水平赋予任何试验内容，虽然试验的数据分析结论将会随着试验工作者的赋值予以变动，但不会影响各个试验水平的分析结论.如果试验没有相遇平衡性的要求，那么对试验因子的各个水平的试验比较将会失去公平，也将不能保证试验的再现性要求.因此，相遇平衡是试验设计的最基本的一种平衡要求.但是，这种平衡性的组合判定方法较为复杂，本文利用矩阵象技术,给出了相遇平衡性的一个等价条件, 借助于SAS软件可以方便快速的进行验证.

1　正交相遇平衡区组设计的定义

在试验设计理论当中，具有两种形式的设计，其一为行列设计，如正交表、均匀设计等，其二为区组设计，如平衡不完全区组设计、正交拉丁方等.

先从任意形式的区组设计考虑起

定义1[3，4]任意具有v个水平b个区组

B1=(b11,…,b1k1)T,…,Bb=(bb1,…,bbkb)T

的设计都称为区组设计，这里bij为整数满足：1≤bij≤v,j=1,…,ki，而ki为区组Bi的大小，即向量Bi的维数.记这样的区组设计为

这里k=(k1,…,kb)T为向量.为了以后叙述方便,我们也把区组设计

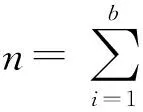
这种形式的区组设计仅仅考虑设计的形状，并不具有设计的优良性.一个设计的优良性，主要体现在各种各样的平衡性.

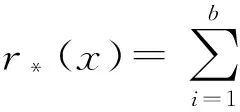
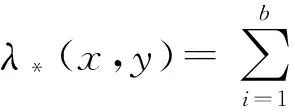
定义3[3，4]将v个水平安排到b个区组B1,B2,…,Bb的一个区组设计Db×k(v)称为相遇平衡的, 假若它满足如下条件:

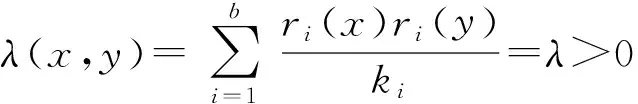
其中λ称为相遇度，相遇度必须大于0才理解为平衡，这个条件称为相遇平衡条件.

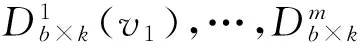
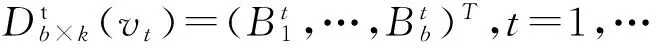
那么n×(m+1)矩阵

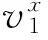
2　区组设计相遇平衡性的等价条件

相遇平衡条件的更一般的形式是

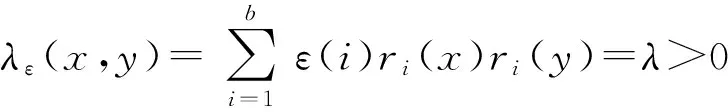
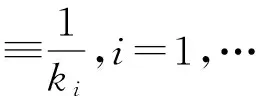
记k=(k1,…,kb)T,r=(r1,…,rb)T,那么一个相遇平衡的区组设计Db×k(v)都可以用参数(v,b,r,k,λ)刻画.常常考虑k=k11b的情况, 其中1b为元素全是1的b维列向量.例如：设B1=(1)、B2=(1,2)T,那么B1、B2就组成了一个区组设计, 记为

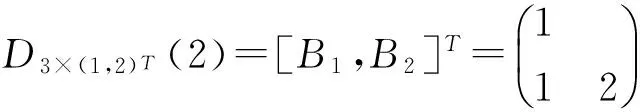
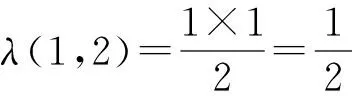
一般地，对于任意的水平数是2的区组设计，只要不是各个区组内仅仅只有一个水平出现，那么相应的区组设计都是相遇平衡的.这说明相遇平衡的条件是比较弱的一个条件.

引理1对于任意区组设计Db×k(v)，我们有

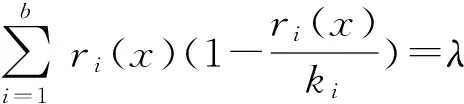
②由于区组设计Db×k(v)是相遇平衡的，即

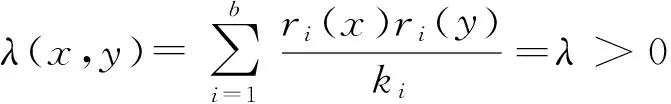
所以

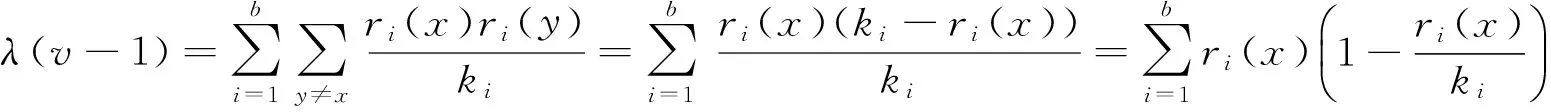
③在ki=k1的条件下，相遇次数为

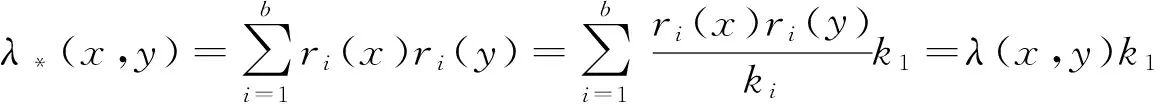
相遇度λ(x,y)是常数当且仅当相遇次数λ*(x,y)是常数.

WTW=CTτkC=λvτv，

此时区组设计D=Db×k(v)的矩阵象为

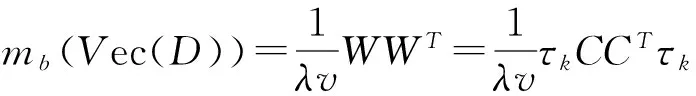
证明首先证明：区组设计D=Db×k(v)是相遇平衡的当且仅当CTτkC=λvτv.

我们利用关联矩阵的定义,并结合相遇平衡性的定义及引理1之②中相遇平衡的等价条件分两步来证明.

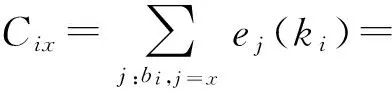
CTτkC的(x,y)号元素为

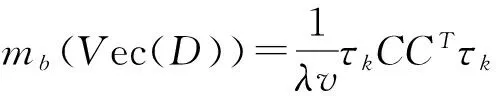
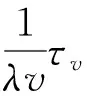
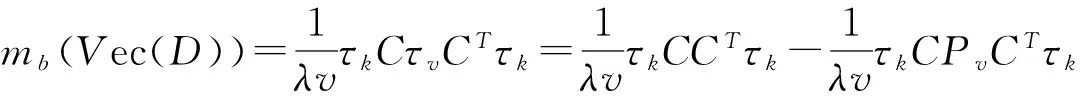
注意到关联矩阵C=Design(Vec(D))的行和是1,所以C1v=1n,而τk1n=0,这样得到τkCPvCTτk=0,从而定理1得证.

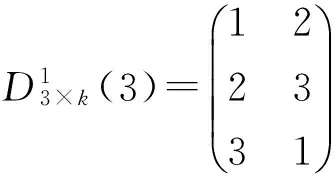
计算可知

其中Vec是矩阵CTτkC的上三角拉长，RC是Vec的极差，RC=0是区组设计为相遇平衡的判定条件.

用定理1可知这个区组设计是相遇平衡的.将这个相遇平衡的区组设计写成广义正交表的形式为

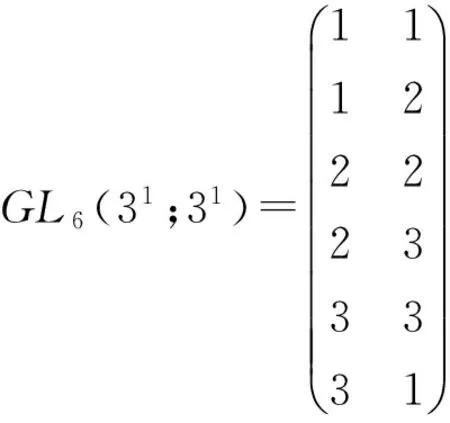
这是一个不饱和的广义正交表，在此广义正交表的基础上，还可以增加一个2水平列，形成饱和的广义正交表GL6(3121;31).

3　 结论

一般的广义正交表GLn(b1v1…vl;vl+1…vm)，其数据分析的优良性质和正交表基本类似，但组合定义性质和正交表的定义有较大差别.而用广义正交表的矩阵象来分析，其矩阵象性质和正交表的矩阵象性质[7,8]又基本类似.实际上，定理1说明：广义正交表的组合相遇平衡性质是它的矩阵象为投影矩阵的一个充分条件.同时广义正交表的组合正交平衡性质是它的各个列矩阵象为相互正交的矩阵的一个充分条件.因此，广义正交表是保证它的各个列的矩阵象是相互正交的投影矩阵的一个充分条件.利用矩阵象作为工具是判定一个设计是否为一个广义正交表的方便和有效的方法.根据多元分析的二次型的克赫伦定理可知，这也是保证广义正交表设计的数据分析结论具有再现性，相应的估计具有无偏和方差最小性质的基本保证.因此，我们建议用广义正交表代替正交表来进行试验设计.

[1]张应山.多边矩阵理论[M].北京:中国统计出版社,1993.

[2]张应山.正交表的数据分析及其构造[D].上海:华东师范大学,2006.

[3]吴亚桢,廖靖宇,张应山,等.正交平衡区组设计统计分析模型的参数估计[J].数学的实践与认识,2012,42(2):200-208.

[4]吴亚桢,廖靖宇,张应山,等.正交平衡区组设计统计分析模型参数估计的分布特征研究[J].数学的实践与认识,2012,42(3):212-221.

[5]廖靖宇,张建军,田萍,等.正交平衡区组设计矩阵象的基本概念及其基本定理[J].数学的实践与认识,2012,42(17):170-177.

[6]罗纯,潘长缘.穷举法寻找正交平衡区组设计[J].应用概率统计,2011,27(1):1-13.

[7]Zhang Yingshan, Lu Yiqiang and Pang Shanqi. Orthogonal arrays obtained by orthogonal decomposition of projection matrices[J].Statistica Sinica, 1999, 9: 595-604.

[8]Pang Shanqi, Zhang Yingshan and Liu Sanyang. Normal mixed difference matrix and the construction of orthogonal arrays[J].Stat. & Prob.Lett, 2004, 69: 431-437.

责任编辑：周伦

The Equivalent Condition of Meeting Balance of Generalized Orthogonal Arrays

WU Ya-zhen1, YANG Lin1, ZHANG Ying-shan2, LIAO Jing-yu1, TIAN Ping1

(1.SchoolofMathsandStatistics，XuchangUniversity，Xuchang461000，China;2.SchoolofStatistics,EastChinaNormalUniversity,Shanghai200241,China)

Generalized orthogonal arrays are similar to the orthogonal arrays,whose data analysis maintains the superiority as orthogonal arrays do, i.e., thatis to say estimation of each factor is unbiased estimation in the sense of variance minimizing, but test tim are remarkably decreased. Meeting balance is one of the two balanced conditions of generalized orthogonal arrays,it is also a basic requirement which orthogonal meeting balanced block design must meet. In this paper,using the matrix images technology, it is to prove an equivalent condition of meeting balance. With the help of SAS software verified quickly and easily.

orthogonal meeting balanced block designs；generalized orthogonal arrays；meeting balance; matrix image

2016-02-12

教育部高校博士点专项基金(44K55050);许昌学院科研基金(2015083)

吴亚桢(1980—)，男，河南许昌人，讲师，硕士，研究方向:应用统计，试验设计.

1671-9824(2016)05-0021-05

O212.6

A