无码载波频率初值估计与导航星识别

卢　欢, 郁　丰, 刘　莹, 朱海微

(1.南京航空航天大学自动化学院, 江苏 南京 210016; 2. 南京航空航天大学航天学院,江苏 南京 210016; 3. 上海卫星工程研究所, 上海 200240)



无码载波频率初值估计与导航星识别

卢欢1, 郁丰2, 刘莹3, 朱海微2

(1.南京航空航天大学自动化学院, 江苏 南京 210016; 2. 南京航空航天大学航天学院,江苏 南京 210016; 3. 上海卫星工程研究所, 上海 200240)

当导航卫星的民码信号不可用时,利用无码载波恢复技术测量各个导航卫星的多普勒频移能够实现多普勒定轨。针对伪码未知的情况,提出了基于相位补偿及数据块累加来增强信号,并结合快速傅里叶变换估计载波频率的方法;为解决无码条件下的导航卫星识别问题,提出了一种基于多普勒频移特征的导航星识别方法,研究了基于三分法快速搜索优化平移量的匹配算法,并采用全局匹配、局部剔除的策略来提高卫星识别的全局可信度。仿真结果表明,对于80ms的卫星中频数据,无码载波频率估计误差保持在7Hz之内,并且正确估计的卫星数在9颗以上;在考虑先验参数不精准及测量误差的情况下,正确识别的卫星数大多为6颗及以上,满足定轨要求的最少卫星数目。

定轨; 无码; 频率估计; 卫星识别; 匹配

0　引　言

卫星轨道参数的精密测定是卫星应用的基础。多普勒定轨是一种测定卫星轨道参数的重要方式。目前主要有两种多普勒定轨方式,一种是利用跟踪与数据中继卫星系统(trackinganddatarelaysatellitesystem,TDRSS)单向多普勒信息测定卫星的轨道[1-2],其测轨原理是中继卫星发射带有自身位置信息的信标信号,卫星接收后,利用超稳晶振提取单向多普勒信息,并根据这些多普勒信息计算出自己的轨道[2-4];另一种是地基多普勒定轨系统,当卫星过境时,利用多普勒频移计算出卫星相对地面站的速度进而确定卫星轨道参数[5-8]。

当卫星导航系统的导航信息的伪随机码不可知,即卫星导航系统在特定区域彻底关闭了明码信号,就不能使用传统的定轨方式测定轨道参数。本文提出了一种基于卫星导航系统的新的多普勒定轨方法,其基本实现原理是在无需伪码的条件下实现载波频率初值估计,作为载波跟踪环的本地频率初值,恢复出目标载波,并测量出各个导航星信号的多普勒频移,然后采用一定的匹配算法寻找出某频移对应的导航星,将导航卫星当作频率已知的无线电信标,从而建立高精度测量模型,结合轨道动力学模型,采用适当的数据融合算法估计出高精度轨道参数。其中,载波跟踪环跟踪恢复载波的条件是得到载波频率的初始估计值。传统的捕获环节利用伪随机码良好的相关特性,完成载波频率和码相位的粗略估计,实现跟踪通道初始化[9-10]。但是,由于平方削弱了信号强度,对平方消码信号直接进行快速傅里叶变换(fastFouriertransform,FFT),几乎检测不到超过阈值的尖峰;而且高动态条件下的多普勒频移搜索范围为几十kHz[11-16],若采用逐步搜索法,会耗费大量时间。所以,载波频率估计值的获取以及各个多普勒频移对应哪颗导航卫星是需要解决的关键问题。

载波频率初值估计是获取载波的初始频率,能否正确估计初值将直接影响到平方环能否正常工作。文献[17]提到了基于相位补偿、同步数据块累加及FFT变换的捕获技术:考虑Lms(L≤20)的卫星中频数据,以1ms(伪码周期)为单位分割为L个长度相同的数据块。经过相位补偿和数据块累加后,分析信号频谱得到载波频率的估计值[17-19]。但是,该算法受数据码周期的限制,最多只能考虑20ms的数据长度;对累加后的信号做频谱分析,并不是所有卫星的信号都会呈现明显的尖峰,往往是信号强度最强的3颗卫星的信号会有超过阈值的尖峰,正确估计频率的卫星数量较少。本文对该算法做了适应性的调整,平方消除了中频信号的调制码,使分块累加的数据长度摆脱了数据码周期的限制,使其在伪码未知情况下可以正确估计较多的卫星数量。

在通常的卫星导航中,是通过伪码匹配的方式来识别导航卫星的,但是无码载波恢复技术[20-22]仅能得到不同频移的单载波信号。限于调研的文献,目前国内外尚没有应用于无码条件下的匹配方法,所以本文提出了基于多普勒频移的导航卫星识别方法。用户卫星初始轨道可以认为是已知的,而导航卫星的星历可以通过地面上注,所以可以计算得到一系列多普勒频移的先验值。由于接收机时钟频差的存在,多普勒频移的先验值与实测值有固定的频率差,通过整体平移使得残差最小,从而识别导航卫星并获取接收机时钟频差。

无码载波频率初值估计及导航卫星识别技术是无码多普勒定轨的关键技术,其原理框图如图1所示。本文提出了基于相位补偿及数据块累加来增强信号并通过FFT估计载波频率的方法和基于多普勒频移特征的导航星识别技术,用于实现接收机的初始化,为实现无码多普勒定轨提供了技术基础。

图1　无码载波频率初值估计及导航星识别技术Fig.1　Codeless carrier frequency initial value estimation and navigation satellite recognition

1　无码载波频率初值估计方法

为了获得无码载波跟踪环的初始频率,本文提出相位补偿及数据块累加来增强信号并结合FFT算法估计载波频率的方法,原理分析如下。

卫星信号经射频前端下变频得到中频复信号,中频数据可表示为

(1)

式中,A为信号的幅度;C(t)为伪随机噪声码,取值为±1;D(t)为导航数据码,取值为±1;f为实际的载波频率;n(t)为噪声信号。

对中频信号r(t)平方消码:

(2)

处于+1状态的调制码,经平方后均为+1,而+1不改变信号相位和载波频率。平方后的载波信号变为连续的二倍频载波,其他两项频谱依然是噪声,用n′(t)表示。

由于信号叠加可增强信号强度,所以考虑将平方信号以T为单位分成L个数据块,对L个数据块叠加:

(3)

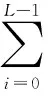
所以,本地产生一个频率为Δf的载波调整信号p(t),对r2(t)进行相位补偿:

(4)

载波调整信号的引入只改变了载波频率,与噪声相乘依然是噪声。类似地,将相位补偿后的信号以T为单位分为L个数据块,并对L个数据块累加:

(5)

式中,f′=2f+Δf。

当f′T=M是一个整数时,才有

(6)

若数据块的长度T=1ms,f′T是整数的条件就是f′是1kHz的整数倍,Δf的搜索范围是[0kHz,1kHz]。

当式(6)成立时,累加后的数据可表示为

(7)

平方信号经相位补偿和数据块累加得到了一个被放大L倍的信号。对增强后的信号做FFT运算,寻找超过门限值的频谱峰值,将尖峰对应的频率值减去Δf再除以2,结果就对应某个卫星信号的实际载波频率。

无码载波频率初值估计算法如图2所示。

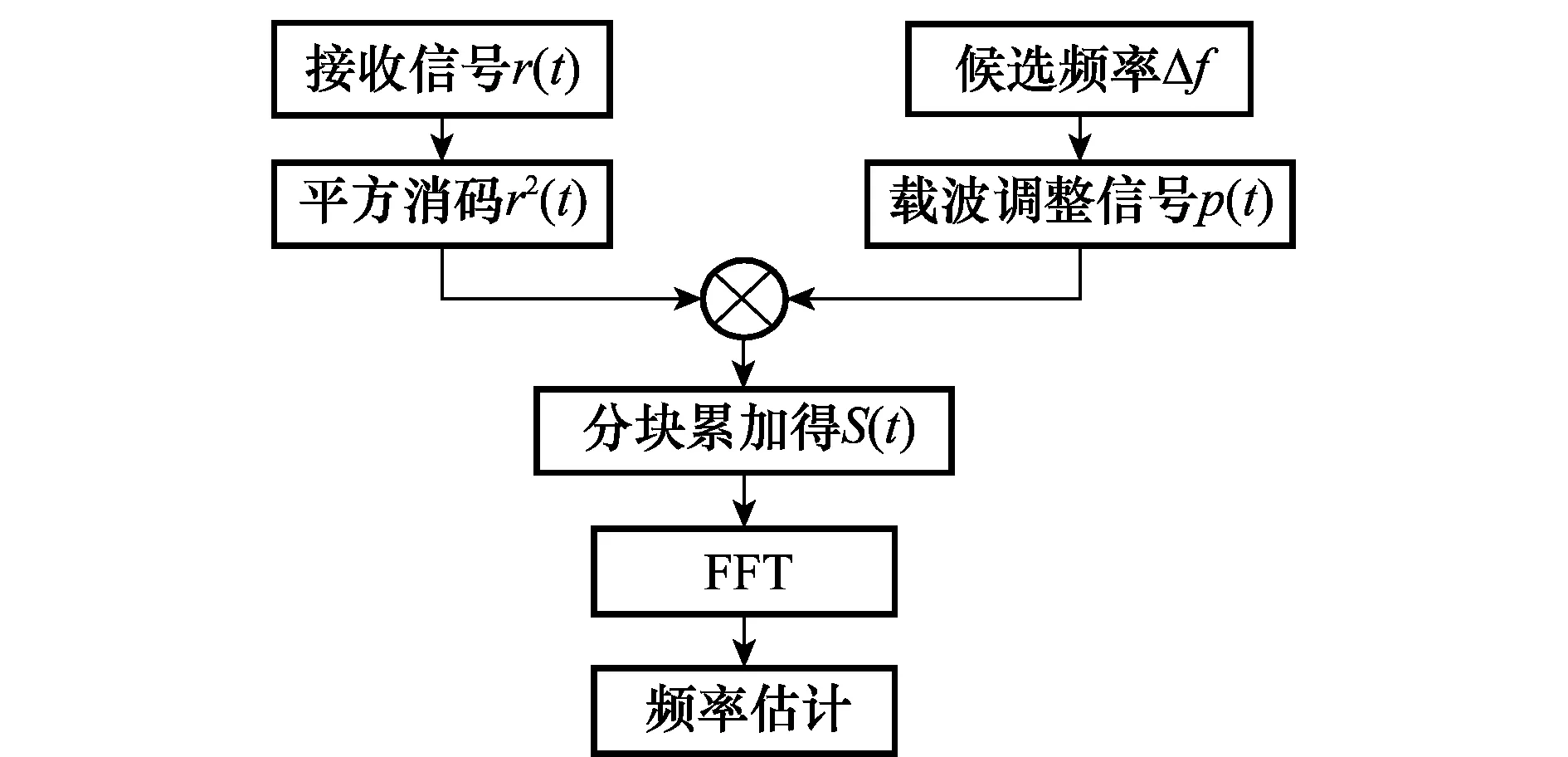
图2　无码载波初值估计算法流程图Fig.2　Chart of codeless carrier frequency initial value estimation

2　导航卫星识别匹配算法

利用得到的频率估计值作为平方环的频率初值,实现对目标载波的连续跟踪,获得了一系列的多普勒频移,但是每个多普勒频移对应哪颗导航卫星仍然是未知的。传统的伪码匹配识别导航卫星的方法已经失效。本文提出了一种基于多普勒频移特征识别导航卫星和估计频差的算法,具体分析如下。

2.1基于频移特征的导航星识别与频差估计指标

假设用户卫星接收到第k颗导航卫星的信号,则接收机测量的多普勒频移可以表示为

(8)

已知初始轨道及上注的导航卫星的星历,可计算得到一系列先验多普勒频移:

(9)

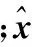
(10)

但是,先验根数的不精准、噪声以及测量误差等因素使得两种频率并不能完全匹配。在大多数频率对齐的基础上,采用全局匹配、局部剔除的策略。即在e最小的情况下,若某颗卫星的匹配残差与总体误差的比值超过门限值M,则剔除对应的实测多普勒频移。剔除多普勒频移的条件可表示为

(11)

2.2匹配算法优化

(12)

在两种频率几乎对齐时,e有一个最小值,所以采用三分法寻找优化平移量,算法步骤如下。

图3　三分法的3种情况Fig.3　Three kinds of situation of trichotomy

步骤 3重复执行步骤1、步骤2,直到m1、m2的距离小于设定阈值,取(m1+m2)/2为优化平移量。

3　仿真及分析

为了对无码载波频率初值估计方法和导航星识别匹配算法进行验证,本文搭建了卫星捕获的仿真平台,其中导航卫星星座由24颗全球定位系统(global positioning system,GPS)卫星组成,用户卫星的初始位置(单位：m)为p=[6 878 137,0,0],初始速度(单位：m/s)为v=[0,-981,7 549];信号载噪比为45 dB-Hz,下变频后信号的中频为0.204 6 MHz,中频数据采样频率为1.023 MHz;锁相环阻尼因子为0.637,环路带宽为20 Hz,积分时间为5 ms,压控振荡器灵敏度为0.008 5 Hz/V;接收机时钟频率误差δf=45 Hz。由无码载波频率估计技术的理论分析可知,累加可以增加信号强度,所以考虑80 ms的数据;数据块越长,搜索范围越小,所得的搜索频率越精确,所以选择数据块的长度为4 ms,对应的搜索频率范围是[0 Hz,250 Hz],搜索步长选为6.25 Hz,可产生41个候选频率。无码载波频率估计方法的估计频率误差如图4所示。从图4中可知,估计误差范围为±5 Hz,与上述分析的理论值6.25 Hz相符。

图4　载波频率估计初值与频率真实值的差值Fig.4　Difference value of carrier frequency 　　　estimated initial value and real value

常规的捕获算法为基于FFT的并行捕获算法,设置频率搜索步长为50 Hz,则由该算法所得的载波频率和码相位的捕获估计值如图5所示。从图5中可得频率和相位估值分别为67 350 Hz和351码片。这种算法的频率估计误差如图6所示,估计误差范围为±35 Hz。

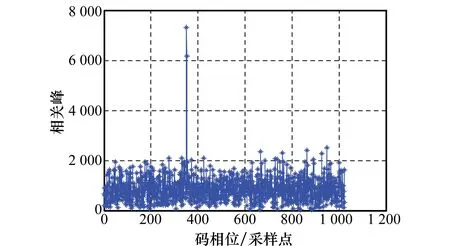
图5　基于FFT的并行捕获实验结果Fig.5　Result of the experiment of FFT parallel capture

图6　并行捕获算法频率估计误差Fig.6　Error of FFT parallel capture

常规算法若要取得与本文算法一致的精度,需要将搜索补偿减小为5 Hz,需要搜索的频率点数目为(75 000/5=15 000)次,在不考虑伪码搜索的前提下,运算次数已经很庞大了。在本文的估计算法中,需要41次FFT运算可以获得载波频率估计值。所以从运算量上看,本文的频率估计算法运算量较小。

表1　多普勒频移优化平移先验值、测量值及频差绝对值

正确识别的卫星数目是评价识别算法最重要的参数,对定轨的实现有直接的影响;导航星正确识别的概率也是评价识别算法的一个指标,将正确识别的卫星数目与可见卫星数目的比值作为评价的依据。图7为100s(以1s为步长,每秒跟踪400ms的卫星中频信号)内,正确识别卫星的数目,从图7中可以看出,正确识别的卫星只在2s、76s、78s的时刻为5颗,大部分时间为6颗及以上,超出了定轨要求的最少卫星数目;图8为100s内卫星正确识别的概率。从图8中可看出,识别正确率极少数为0.6,大部分在0.8附近。

图7　正确识别的卫星数目Fig.7　Number of properly identify satellites

图8　导航卫星正确识别的概率Fig.8　Probability of properly identify of satellites

(1) 先验根数的不准确对匹配的影响

使用卫星轨道真值获得多普勒频移的真实值,轨道参数插值获得多普勒频移先验值。两组频率的差值即为先验根数不精准对匹配的影响。以第8颗可见卫星为例,频差如图9所示,从图中可以看出,先验根数的不精准产生多普勒频移误差为±0.15Hz,对匹配的影响较小。

(2) 测量误差对匹配的影响

由轨道真值获得多普勒频移的真实值,由平方环获得多普勒频移的测量值,两种频率的差值即为环路的测量误差。以第5颗可见星为例,所得频差如图10所示。从图中可以看出,环路稳定时,频差在均值为0,波动为±15Hz的范围内振动。这说明测量误差对匹配的影响比较大。所以,测量误差是多普勒频移误匹配的主要原因。

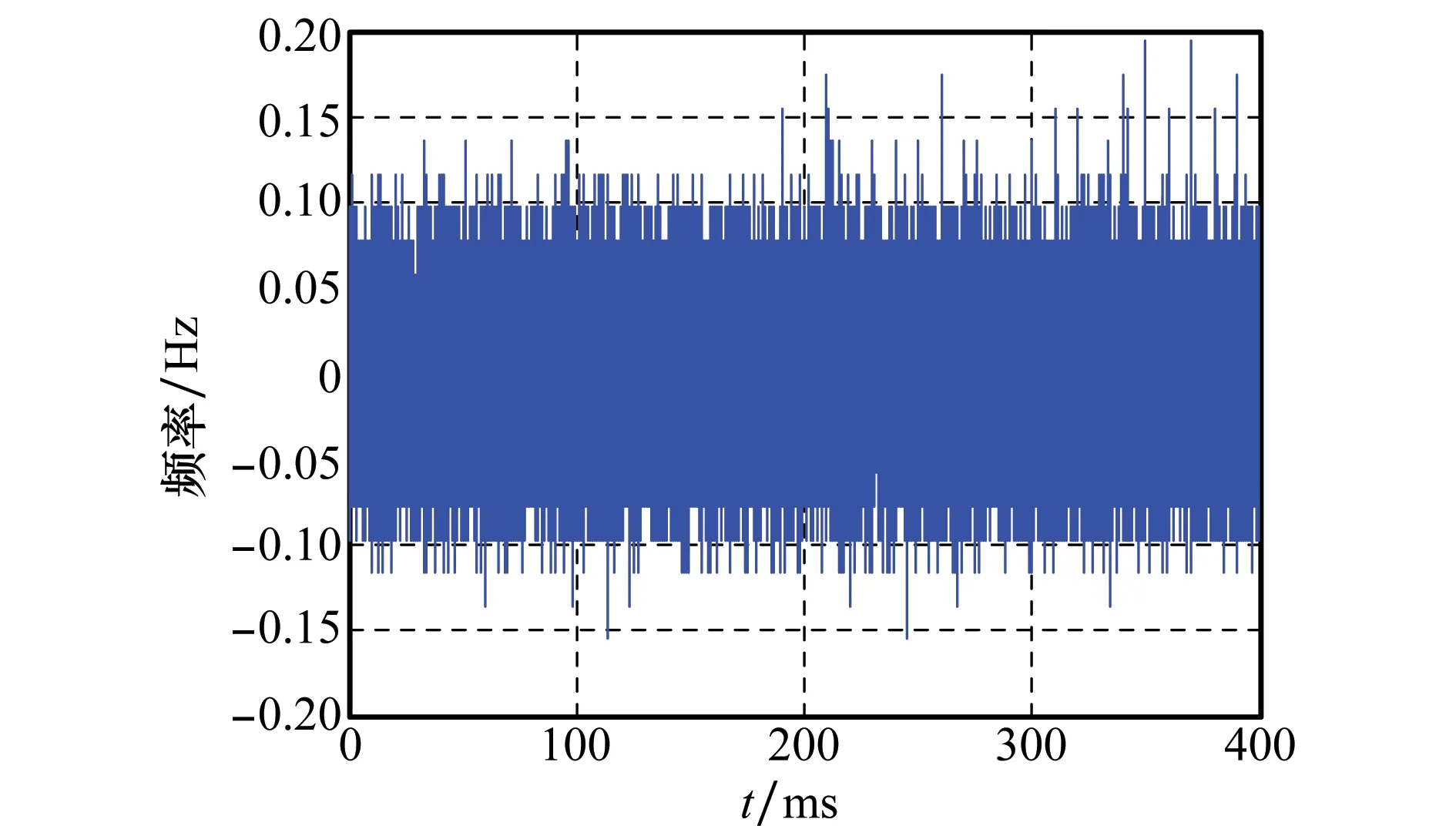
图9　多普勒频移的真实值与先验值之差Fig.9　Difference frequency of empirical value and real frequency

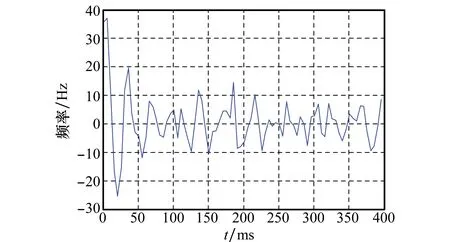
图10　多普勒频移的真实值与测量值之差Fig.10　Difference frequency of empirical value and measurement

4　结　论

本文提出了一种基于卫星导航系统的新的多普勒定轨方法,并研究了其关键技术:无码载波频率初值估计和导航卫星的识别匹配。本文首先提出了基于相位补偿和数据块累加提高信号强度,并通过FFT估计载波频率的方法;接着对提出的基于多普勒频移特征的导航卫星识别技术进行了阐述,使用三分法寻找优化平移量,提高了卫星识别的效率;最后利用仿真的中频数据对两种算法进行仿真验证。仿真结果表明,在伪码未知条件下,无码载波初值估计算法大多数时间里可以正确估计9颗卫星;在各种误差存在的情况下,导航卫星识别算法基本可以正确识别6颗及以上的卫星,满足定轨要求。

[1]NingXL,FangJC.Spacecraftautonomousnavigationusingunscentedparticlefilter-basedcelestialDopplerinformationfusion[J].Measurement Science & Technology,2008, 19(9):44-46.

[2]GramlingCJ,LongAC.AutonomousnavigationusingtheTDRSSonboardnavigationsystem(TONS)[J].Advances in Space Research, 1995, 16(12):77-80.

[3]WangFX,LuBY,ZhouZM.ResearchonautonomousnavigationmethodusingTDRSS[J].Space Electronic Technology,2005,2(3):8-13. (王飞行,陆必应,周智敏.利用TDRSS自主导航定位的方法研究[J].空间电子技术2005,2(3):8-13.)

[4]WuTY,WuSQ.ComparisonbetweenseveralsatelliteconstellationschemesforME-OTDRSSofChina[J].Journal of Systems Engineering and Electronics, 2008,19(5):907-913.

[5]ZhaoL,DingJC,MaXF. Satellite navigation principles and applications[M].Xi’an:NorthwesternPolytechnicalUniversityPress, 2011:78-110.(赵琳,丁继成,马雪飞. 卫星导航原理与应用[M].西安:西北工业大学出版社,2011:78-110.)

[6]TsuiJ. Fundamentals of global positioning system receivers-a software approach[M].Hoboken,NJ:Wiley, 2005: 224-270.

[7]KaplanED,HegartyC. Understanding GPS: principles and applications[M].2nded.Boston:ArtechHouse,2006: 153-240.

[8]MisraP,EngeP. Global positioning system: signals, measurements and performance[M].Lincoln:GangaJamunaPress, 2006: 431-498.

[9]ZengQX,TangLL,WangQ,etal.AcquisitionoffinecarrierfrequencyunderwidecarriertonoiseratioinGPSsoft-warereceivers[J].Journal of Chinese Inertial Technology,2013,21(4):500-505.(曾庆喜,唐琳琳,王庆,等.GPS软件接收机宽载噪比载波频率精确捕获策略[J].中国惯性技术学报,2013,21(4):500-505.)

[10]ZhangWM,ZhouYY,JiangL.AnalysisofthesignalacquisitionperformanceoftheGPS[J].Systems Engineering and Electronics, 2012, 34(10):73-75.(张文明,周一宇,姜利.GPS信号捕获性能的分析[J].系统工程与电子技术，2012,34(10):73-75.)

[11]DongZH,WuSL.NewacquisitionmethodforDSSSwithlargeDoppler[J].Systems Engineering and Electronics,2008, 30(8):1424-1426.(董智红,吴嗣亮. 大多普勒偏移下直接序列扩频信号捕获新方法[J].系统工程与电子技术，2008,30(8):1424-1426.)

[12]PsiakiML.BlockacquisitionofweakGPSsignalsinasoftwarereceiver[C]∥Proc.of the Institute of Navigation GPS, 2001:2838-2850.

[13]SpangenbergSM,ScottI,McLaughlinS,etal.AnFFT-basedapproachforfastacquisitioninspreadspectrumcommunicationsystems[J].Wireless Personal Communications,2000,13(1/2):27-55.

[14]BetzJ,CapozzaP,FiteJ.Systemfordirectacquisitionofreceivedsignals[P].US:20040071200,2004.

[15]PatelV,ShuklaP.FastermethodsforGPSsignalacquisitioninfrequencydomain[C]∥Proc.of the IEEE International Conference on Emerging Trends in Networks and Computer Communications, 2011: 84-88.

[16]ZhuXF,ChenXY,TuGY,etal.Newhigh-sensitivityacquisitionmethodandimplementationforGNSSsoftwarereceiver[J].Systems Engineering and Electronics, 2009,31(9): 2055-2058. (祝雪芬,陈熙源,涂刚毅,等.GNSS软件接收机新型高灵敏度捕获算法及实现[J].系统工程与电子术，2009,31(9):2055-2058.)

[17]LuY. GPS global positioning receiver-principle and software implementation[M].Beijing:ElectronicIndustryPress, 2009:58-67.(鲁郁.GPS全球定位接收机——原理与软件实现[M].北京:电子工业出版社,2009:58-67.)

[18]ChenK,WangSC,ZhaoX,etal.Delayingwithmultiplyingandsynchronousdatablockaccumulation-basedalgorithmforGPSsignalacquisition[J].Science Technology and Engineering, 2012, 36(12):9845-9850. (陈科,王仕成,赵欣,等. 基于延时相乘和同步数据块累加的GPS捕获算法[J].科学技术与工程,2012,36(12):9845-9850.)

[19]BorioD.Squaringandcross-correlationcodelesstracking:analysisandgeneralisation[J].IET Radar,Sonar and Navigation,2011,5(9): 958-969.

[20]BorioD,RaoM,DriscollCO.Codelessprocessingofbinaryoffsetcarriermodulatedsignals[J].IET Radar, Sonar and Navigation, 2013, 7(2): 143-152.

[21]JewellD.GPSL2P(Y)phaseshift[J].GPS World, 2010, 21(1):22-23.

[22]MaJW.Codelessandsemi-codelesstrackingtechnologyresearchandimplementationintheGPSreceiver[J].Science and Technology Information, 2014,12(4): 165-166.(麻军伟.GPS接收机无码半无码跟踪技术的研究与实现[J].科技信息,2014,12(4):165-166.)

Codeless carrier frequency initial value estimation andnavigationsatelliterecognition

LU Huan1, YU Feng2, LIU Ying3, ZHU Hai-wei2

(1.College of Automation Engineering, Nanjing University of Aeronautics & Astronautics,Nanjing 210016, China; 2. College of Astronautics, Nanjing University of Aeronautics & Astronautics,Nanjing 210016, China;3.Shanghai Institute of Satellite Engineering, Shanghai 200240, China)

ThereisawayofDopplerorbitdeterminationthatrecoverscarriersignaleffectively,andmeasurestheDopplerfrequencyshiftpreciselywhencivilcodesofsatellitenavigationsignalsarenotavailable.Forunknownpseudo-code,amethodbasedonphasecompensationanddatablockaccumulationispresentedtoestimatethecarrierfrequencyofthesquaresignalaccurately.Forcodelessnavigationsatelliteidentification,amethodbasedonthecharacteristicsofDopplerfrequencyshiftisproposed,andtheclockfrequencyoffsetofthereceiverisreceived,andthematchalgorithmbasedonthethreepointsmethodisresearched.Theglobalmatch,localeliminationstrategyisadopttoimprovethereliabilityofsatelliterecognition.Thesimulationrevealsthatcodelesscarrierfrequencyestimationerroriswithin7Hz,andthenumberofsatellitesestimatedcorrectlyis9ormore.Consideringtheinaccuracypriorparametersandmeasurementerrors,atleast6satellitesareidentifiedcorrectly,whichsatisfiestherequirementoforbitdeterminationofsatellites.

orbitdetermination;codeless;frequencyestimation;satelliterecognition;match

2015-06-24；

2015-12-18；网络优先出版日期：2016-07-05。

国家自然科学基金(61203197)；上海航天科技创新基金(SAST201424)资助课题

V448.2

ADOI:10.3969/j.issn.1001-506X.2016.10.20

卢欢(1992-),女,硕士研究生,主要研究方向为卫星软件接收机卫星应用。

E-mail:luhuan5566@126.com

郁丰(1980-),男,副研究员,博士,主要研究方向为微小卫星姿态轨道控制技术、航天器自主导航。

E-mail:yufeng@nuaa.edu.cn

刘莹(1988-),女,助理工程师,硕士,主要研究方向为小卫星、纳米卫星技术。

E-mail:xy1617@qq.com

朱海微(1993-),女,硕士研究生,主要研究方向为卫星导航、惯性导航及组合导航系统。

E-mail:zhhwwei@163.com

网络优先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160705.1730.010.html