海洋环境下混凝土方桩使用寿命预测模型

李镜培, 李　鹤

(1.同济大学 岩土及地下工程教育部重点实验室,上海 200092;2.同济大学 土木工程学院,上海 200092)



海洋环境下混凝土方桩使用寿命预测模型

李镜培1,2, 李鹤1,2

(1.同济大学 岩土及地下工程教育部重点实验室,上海 200092;2.同济大学 土木工程学院,上海 200092)

基于Fick第二定律，建立了考虑扩散系数时变性、荷载对扩散系数影响和氯离子结合能力的氯离子扩散方程；通过求解扩散方程得到考虑多因素影响的混凝土方桩使用寿命预测模型；并分析了桩的保护层厚度、裂缝控制宽度、表面氯离子浓度和临界氯离子浓度等因素对桩的使用寿命的影响.分析结果表明：得到的氯离子扩散方程与实测数据吻合较好；对于设计使用寿命为50年的混凝土方桩，保护层厚度应大于45 mm，桩身裂缝宽度不宜大于0.1 mm.

混凝土耐久性； 钢筋混凝土方桩； 氯离子扩散； 使用寿命

伴随着港口码头的兴建，近海建筑物的建造，大量的预制钢筋混凝土方桩被用于建设中.而近海及海洋环境中存在大量的氯离子，使得桩基础内部钢筋很容易发生锈蚀，进而降低结构的承载能力，影响结构的耐久性.目前，关于海洋环境下混凝土结构耐久性问题的研究大多是针对普通混凝土结构，对于钢筋混凝土方桩的氯离子侵蚀问题的研究并不多见.

已有研究[1-3]表明，氯离子在混凝土中的扩散系数并不是定值，会受到时间、荷载和氯离子结合能力等因素的影响.Dhir等[4]建立了简单扩散情况下的混凝土耐久性寿命预测模型，但是并未考虑扩散系数的时变性和荷载等因素对扩散的影响；Khatri[2]建立了考虑扩散系数随时间变化的海洋环境混凝土结构使用寿命预测模型，但并未考虑荷载对扩散系数的影响；余红发等[3]建立了考虑时间、荷载和氯离子结合性能等多种因素的混凝土结构使用寿命预测模型，但该模型并不适用于对桩基础的寿命预测.李镜培等[5]、邵伟等[6]对海工环境下的预应力高强度混凝土(PHC)管桩进行寿命预测，但同样假设氯离子扩散系数为定值，并且氯离子在管桩与方桩中的扩散方程也存在差异.

鉴于此，本文基于Fick第二定律，提出海洋环境下，考虑扩散系数时变性、氯离子结合能力和荷载影响的混凝土方桩中氯离子的扩散方程；通过求解扩散方程得到氯离子侵蚀环境下混凝土方桩耐久性寿命预测模型；分析了桩身裂缝宽度、表面氯离子浓度和临界氯离子浓度对桩的耐久性寿命的影响，针对设计使用寿命为50年的方桩提出了最小保护层厚度和最大裂缝宽度，并提出了提高桩基础使用寿命的措施.

1　氯离子扩散方程

1.1混凝土中氯离子的扩散方程

氯离子在混凝土结构中的扩散，可以利用Fick第二定律来描述，扩散方程为[7]

(1)

式中：t为混凝土结构暴露于氯离子环境中的时间,年；x为氯离子侵蚀的深度,mm；D为氯离子扩散系数,m2·s-1；C为氯离子浓度(混凝土质量百分比).

式(1)是在假定氯离子在混凝土中的扩散系数为常数的前提下得到的，但实测数据[1,8]表明，扩散系数随混凝土结构龄期的增长会逐渐减小.考虑到氯离子扩散系数的时间依赖性，可以采用式(2)计算扩散系数[4,8]：

(2)

式中，D和D0分别为扩散时间为t和t0时混凝土的氯离子扩散系数；m为时间依赖性系数.

当混凝土结构在使用过程中受一定程度的荷载作用时，其内部结构会发生变化，从而影响氯离子在混凝土中的渗透性[9].

一般将混凝土的应力水平作为评价依据[10-11]，得到考虑荷载影响的氯离子扩散系数Dσ计算公式：

(3)

式中,f(σ)为与混凝土应力σ有关的函数表达式，可由试验拟合得到.

通过混凝土的应力水平来考虑荷载对扩散的影响时，仅考虑了混凝土保护层产生应力但未开裂的情形，这并不适用于那些在实际使用过程当中存在裂缝的钢筋混凝土结构.

对于混凝土桩基础，在其运输和沉桩过程中不可避免地存在微裂缝；当受到外荷载作用时其受拉侧也会产生荷载裂缝，由于保护层已经开裂，式(3)已经不再适用.此时，可以通过考虑外荷载产生的钢筋拉应力来考虑荷载产生的应力和裂缝对扩散的影响[12]：

(4)

式中:σs为钢筋拉应力；A为荷载影响系数，一般通过试验得到.

如此，便得到了考虑荷载影响和扩散系数随时间变化的桩基础混凝土氯离子扩散系数计算公式：

(5)

式中，m为时间依赖性系数.

当氯离子进入混凝土结构内部后，一部分被水泥水化产物固化，这部分氯离子被称为结合氯离子(Cb)，并不会引起钢筋的锈蚀；另一部分溶解于混凝土孔隙液中，在混凝土中迁移，被称为自由氯离子(Cf)，当自由氯离子在钢筋表面积聚到一定程度后会引起钢筋的锈蚀[13].

为方便求解扩散方程，假定氯离子结合能力为线性的，则有：

(6)

式中:Cb为结合氯离子浓度；Cf为自由氯离子浓度.式(6)可以转换为

(7)

式中,k为氯离子结合系数.

将式(5)和式(7)代入式(1)便可得到氯离子的扩散方程：

(8)

对于预制混凝土方桩，可以认为混凝土内部的初始氯离子浓度C0=0，则有：初始条件为t=0，x>0时，C=C0=0；边界条件x=0，t>0时，C=Cs.则可以求解得到氯离子扩散理论模型：

(9)

1.2使用寿命预测模型

海洋环境下钢筋混凝土结构的耐久性寿命一般包括腐蚀诱导期、发展期和失效期3个阶段[14]：诱导期是指氯离子经过保护层扩散到钢筋表面并积累达到钢筋锈蚀临界浓度(Ccr)的时间；发展期是指从钢筋开始锈蚀到保护层开裂的时间；失效期是指保护层开裂到结构完全破坏的时间.由于发展期和失效期时间较短，一般将诱导期的寿命作为混凝土的耐久性寿命，此种计算方式偏于保守，可以满足工程的实际需求.

将C=Ccr代入式(9)可得到钢筋表面氯离子浓度达到临界值的时间，也就是桩基础的耐久性使用寿命预测模型为

(10)

式中，erf-1(·)为erf(·)的逆函数.

2　参数的选取

2.1时间依赖性系数

美国Life-365软件[15]中规定时间依赖性系数m=0.2+0.4(F/50+S/70)，其中F为粉煤灰掺量百分比，S为矿渣掺量百分比；我国《混凝土结构耐久性评定标准》[16]提出对于普通硅酸盐混凝土可以近似取m=0.2；本文研究无掺料的普通硅酸盐混凝土桩，因此取m=0.2进行计算.

2.2初始氯离子扩散系数

一般选取龄期28 d的混凝土扩散系数D0作为初始氯离子扩散系数，可以采用实测数据进行计算；当无实测数据时可以采用式(11)计算[15]：

(11)

式中，w/c为混凝土的水灰比.

2.3钢筋拉应力

外荷载作用下桩身钢筋拉应力σs可以通过桩身的裂缝控制宽度来计算.《混凝土结构设计规范》[17]提供了钢筋混凝土构件最大裂缝宽度wmax的计算模型，其计算公式为

(12)

式中：αcr为构件受力特征系数；ψ为裂缝间纵向受拉钢筋应变不均匀系数，ψ=1.12-0.65ftk/ρteσs；σs为按荷载准永久组合计算的钢筋混凝土构件纵向受拉钢筋应力,MPa；ρte为按有效受拉混凝土截面面积计算的纵向受拉钢筋配筋率，ρte=As/(0.5bh)，b为构件宽度,mm，h为构件高度,mm；Es为钢筋弹性模量,MPa；d为最外层纵向受拉钢筋外边缘至受拉区底边的距离,mm；deq为受拉区纵向钢筋的等效直径,mm；ftk为混凝土轴心抗拉强度,MPa.

2.4荷载影响系数

Konin等[12]通过试验得到轴拉荷载作用下荷载影响系数A=5.98×10-8；Francois等[18]通过试验得到弯拉荷载作用下荷载影响系数A=1.64×10-8.Francois的试验方法更符合荷载作用下桩的受力特点，因此，取A=1.64×10-8更符合实际情况.

2.5氯离子结合系数

日本海港研究所[19]通过对暴露于海洋环境中10～30年的混凝土试块中总氯离子和自由氯离子含量的测试，得到混凝土中总氯离子含量Ct和自由氯离子含量Cf的关系，见表1.

表1混凝土中总氯离子含量与自由氯离子含量的关系

Tab.1Relationship between total chloride ion content and free chloride ion content in concrete

混凝土种类关系OPC(普通混凝土)Ct=1.160CfSCA(掺量5%～30%的矿渣混凝土)Ct=1.153CfSCB(掺量30%～60%的矿渣混凝土)Ct=1.113CfFACB(掺量5%～10%的粉煤灰混凝土)Ct=1.221Cf

本文仅考虑无掺料的普通混凝土桩，按照表1数据可取Ct=1.160Cf，即氯离子结合系数k=0.160.

3　预测模型的验证

实际中关于混凝土结构使用寿命的相关试验和现场监测资料是很少见的.为了验证本文理论模型的可靠性，并说明在氯离子扩散方程中考虑扩散系数随时间变化的必要性，可以对氯离子浓度理论预测值与相关试验的实测值进行对比.若与不考虑扩散系数时变得到的理论值相比，按本文扩散方程得到的理论值与实测值吻合得更好，则可以说明考虑扩散系数时变性是必要的，同时也可以证明本文所建立的扩散方程的正确性.由于使用寿命t是由氯离子扩散理论模型经过严密的数学推导求解得到的，那么基于该方程建立的寿命预测模型也是可行的.

将本文扩散方程式(10)的理论值和不考虑扩散系数时变的理论值与文献[12]实测值进行对比，该文献中分别采用普通混凝土试块和高强度混凝土试块进行氯离子侵蚀试验.

原文实测普通混凝土试块28 d龄期的扩散系数为D0=2.48×10-12m2·s-1，表面氯离子浓度Cs=0.25%，试验所施加的钢筋应力σs=171 MPa.高强度混凝土试块28 d龄期的扩散系数为D0=2.08×10-12m2·s-1，表面氯离子浓度Cs=0.15%，试验所施加的钢筋应力σs=179 MPa.按本文扩散方程和不考虑扩散系数时变性计算得到的自由氯离子浓度理论值与原文侵蚀1年的实测值关系分别见图1和图2.

由图1和图2可以看出，若不考虑扩散系数的时变性，得到的理论值要比实测值大很多，这是由于忽略了扩散系数随时间衰减规律造成的，而考虑扩散系数的时变性的理论值与实测数据吻合较好，说明在实际过程中应该充分考虑扩散系数的时变性.由图中曲线验证了本文氯离子扩散理论方程的正确性，从而也反映了由扩散方程得到的寿命预测模型式(10)的可行性.

图1　普通混凝土中氯离子浓度理论值与实测值对比

Fig.1Comparison of theoretical and experimental chloride concentration in ordinary concrete

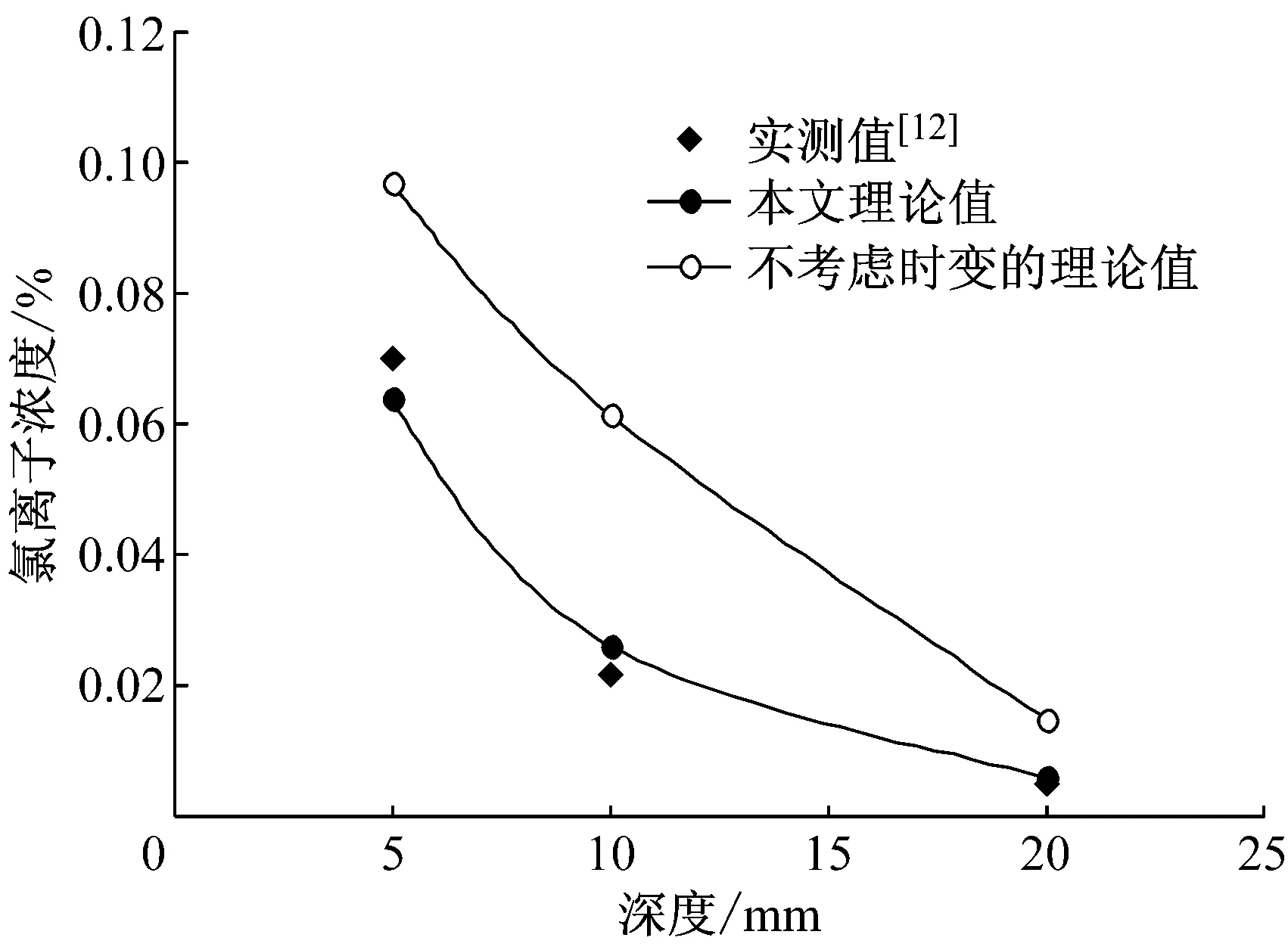
图2　高强度混凝土中氯离子浓度理论值与实测值对比

Fig.2Comparison of theoretical and experimental chloride concentration in high strength concrete

4　工程应用及影响因素分析

4.1工程应用

以某海洋环境下承受水平荷载作用的混凝土桩基础为例进行分析，相关参数如下：截面尺寸为500 mm×500 mm，混凝土强度等级为C40，水灰比为0.4，纵筋为8φ22，保护层厚度45 mm，裂缝宽度限值为0.2 mm.

现场调查结果[20]得到桩基础表面氯离子浓度Cs=0.56%～0.65%，取表面氯离子浓度Cs=0.60%；由w/c=0.35，由式(11)计算可得初始扩散系数为D0=6.91×10-12m2·s-1，临界氯离子浓度参考Duracrete文件[21]水下区临界氯离子浓度取值标准，取Ccr=0.35%；由裂缝宽度限值ωmax=0.2 mm，由式(12)计算可得钢筋拉应力σs=174 MPa.将上述参数代入式(10)可以得到本工程所用桩基础的耐久性使用寿命预测值为：t=47.76年.

4.2影响因素分析

钢筋混凝土桩的耐久性使用寿命主要受保护层厚度、裂缝控制宽度、表面氯离子浓度和临界氯离子浓度等因素的影响，以第4.1节工程实例为背景对各因素进行分析.

4.2.1保护层厚度

图3给出了桩的使用寿命与保护层厚度之间的关系曲线.从图中可以看出：随着保护层厚度的增加，桩的使用寿命显著增加.这是因为保护层厚度的增加，延长了钢筋表面氯离子浓度达到临界浓度的时间，因而，提高了桩的使用寿命.

由图3中数据可知，对于设计使用寿命为50年的混凝土方桩，保护层厚度应大于45 mm，同时可以适当增大保护层厚度来延长混凝土桩的使用寿命.

4.2.2裂缝宽度

采用式(12)可以计算得到裂缝宽度与钢筋应力关系，见表2.

表2裂缝宽度与钢筋应力关系

Tab.2Relationship between cracking width and reinforcement stress

裂缝宽度/mm0.10.20.3钢筋应力/MPa137174210

将钢筋应力代入式(10)可以计算得到桩基础的使用寿命，从而可以得到使用寿命与裂缝宽度的关系曲线，如图4所示.由图可见：随着裂缝宽度的增大，桩的使用寿命显著降低.这是因为裂缝的增大加快氯离子的侵蚀，从而缩减了钢筋表面氯离子达到临界浓度的时间，进而降低了桩的使用寿命.

由图中数据可知，对于设计使用寿命为50年的混凝土方桩，桩身裂缝宽度不宜大于0.1 mm.因此，实际工程中应严格控制桩身裂缝宽度，以保证混凝土桩能满足设计使用寿命的要求.

4.2.3表面氯离子浓度

图5给出了桩的使用寿命与表面氯离子浓度的关系曲线.由图可见：随着表面氯离子浓度的增加，桩的寿命急剧减小.这是因为表面氯离子浓度的增加，使得混凝土桩内外的氯离子浓度梯度增大，加快了氯离子在混凝土中的扩散，从而减小了钢筋锈蚀初始阶段的时间.因而，可以通过混凝土中添加防盐蚀剂和在桩身涂刷环氧树脂等方法来减小桩表面氯离子浓度，从而延长桩的使用寿命.

图3　使用寿命与保护层厚度曲线

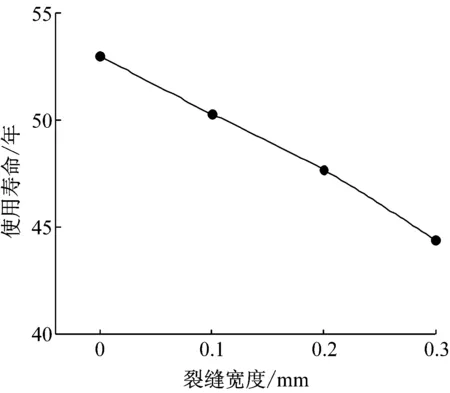
图4　使用寿命与裂缝宽度曲线

4.2.4临界氯离子浓度

图6给出了使用寿命与临界氯离子浓度曲线.由图可见：随着临界氯离子浓度的增大，桩的使用寿命显著增加.这是因为临界氯离子浓度增大，延长了钢筋发生锈蚀的时间，因而延长了桩的使用寿命.因此，可以通过在钢筋表面涂刷环氧树脂和添加阻锈剂等方式来提高临界氯离子浓度，从而延长桩的使用寿命.

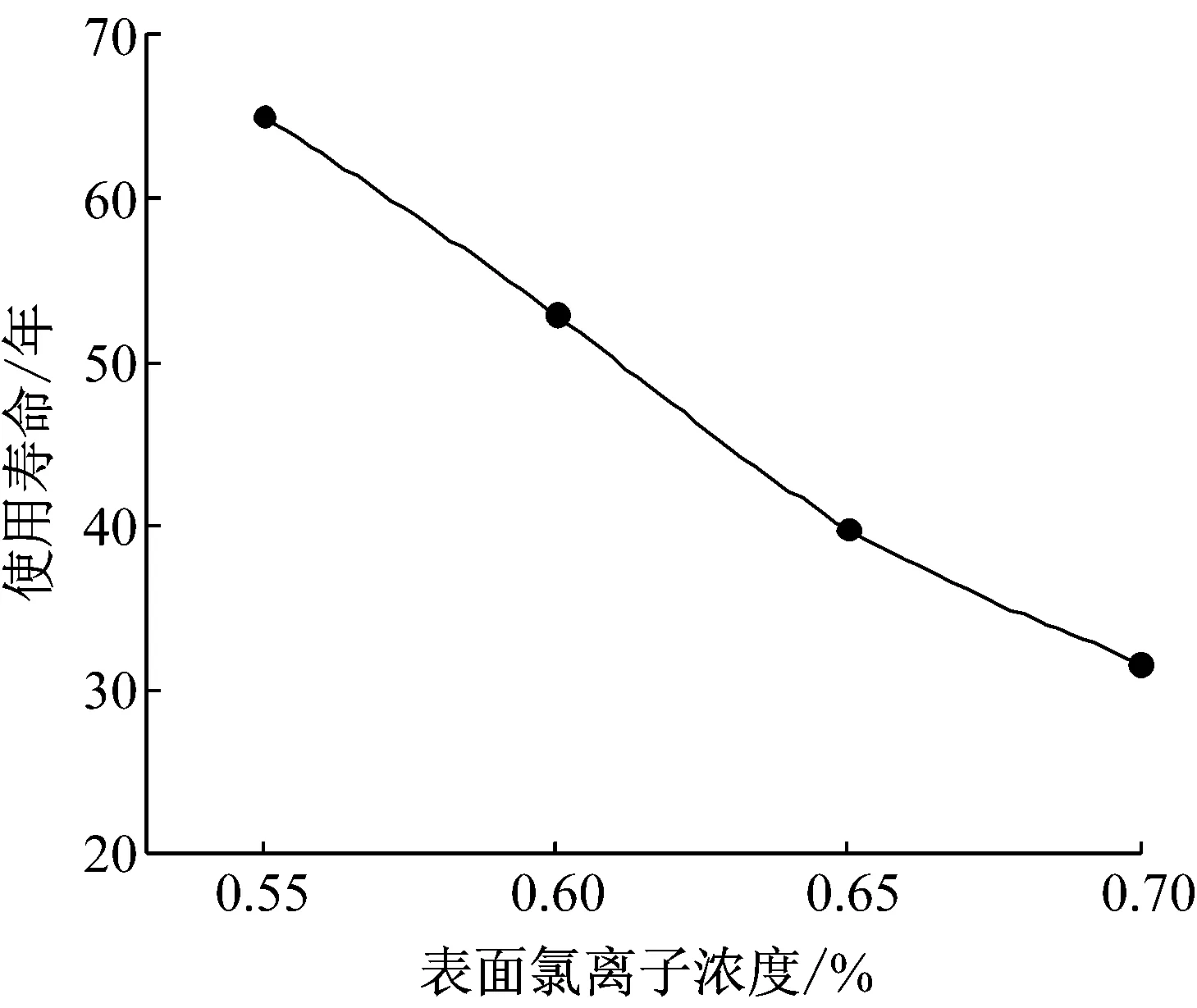
图5　使用寿命与表面氯离子浓度曲线

Fig.5Curve of service life and surface chloride ion concentration

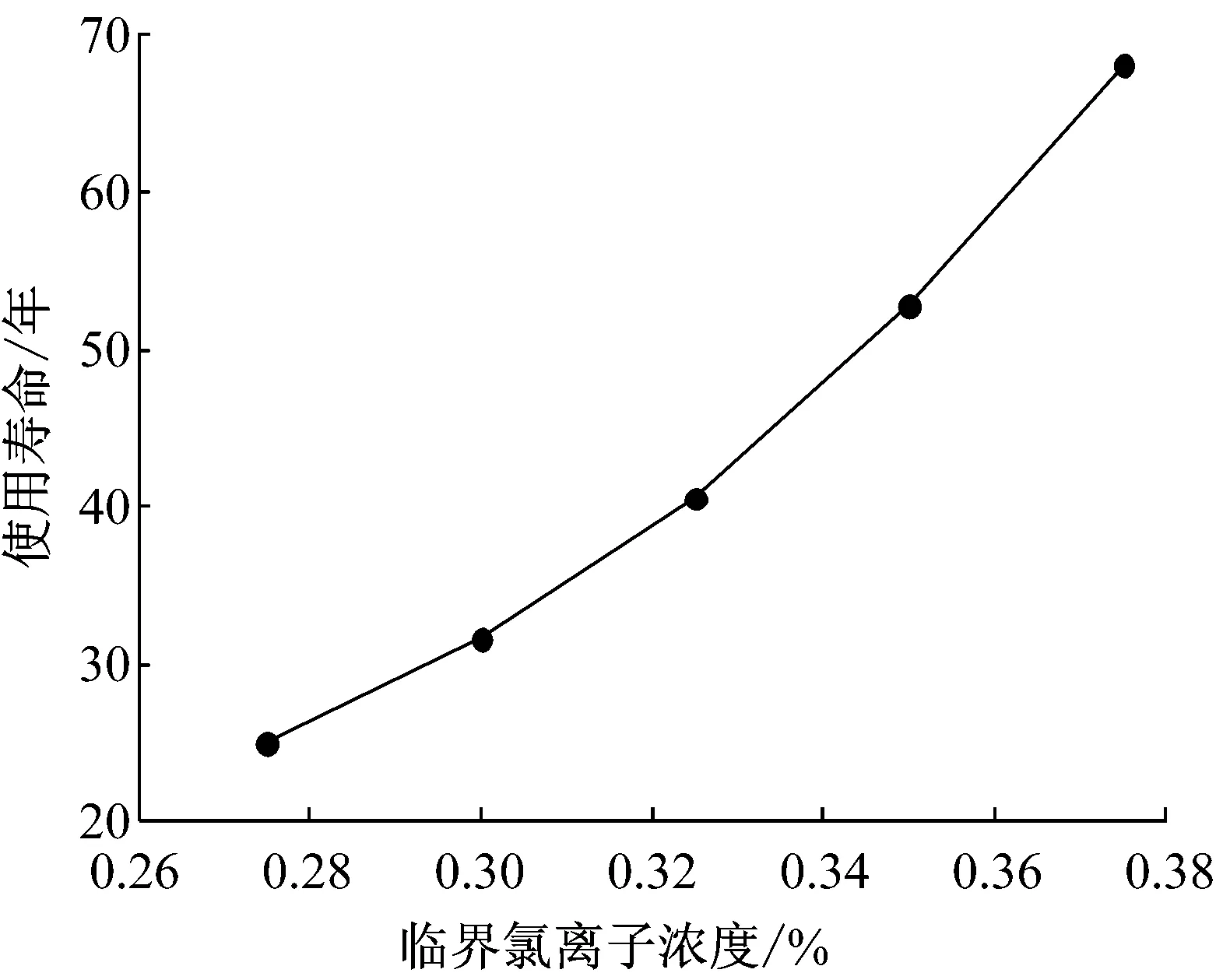
图6　使用寿命与临界氯离子浓度曲线

5　结论

(1)基于Fick第二定律，建立了考虑扩散系数时变性、荷载对扩散系数影响和氯离子结合能力的氯离子扩散方程，并得到混凝土方桩使用寿命预测模型，与相关文献的试验结果进行对比，验证了模型的正确性；

(2)桩身裂缝宽度和表面氯离子浓度的增大，加快了氯离子在混凝土桩中的扩散，降低了桩的使用寿命；保护层厚度和临界氯离子浓度的增大，延长了钢筋表面氯离子浓度达到临界值的时间，提高了混凝土桩的使用寿命.

(3)可以通过在钢筋表面或桩身涂刷环氧树脂和在混凝土内添加阻锈剂或防盐蚀剂等方式提高桩的使用寿命.

(4)对于设计使用寿命为50年的钢筋混凝土方桩，保护层厚度应大于45 mm，桩身裂缝宽度不宜大于0.1 mm.

[1]Mangat P S, Limbachiya M C. Effect of initial curing on chloride diffusion in concrete repair materials[J]. Cement and Concrete Research, 1999, 29(9): 1475.

[2]Khatri R P, Sirivivatnanon V. Characteristic service life for concrete exposed to marine environments [J]. Cement and Concrete Research , 2004, 34(5): 745.

[3]余红发, 孙伟, 麻海燕, 等. 混凝土在多重因素作用下的氯离子扩散方程[J]. 建筑材料学报, 2002, 5(3): 240.

YU Hongfa, SUN Wei, MA Haiyan,etal. Diffusion equations of chloride ion in concrete under the combined action of durability factors[J]. Journal of Building Materials, 2002, 5(3): 240.

[4]Dhir R K, Jones M R, Ahmed H. Concrete durability: estimation of concentration during design life[J]. Magazine of Concrete Research, 1991, 43(154): 37.

[5]李镜培, 岳著文, 邵伟, 等. 海工环境PHC管桩设计寿命计算[J]. 硅酸盐学报, 2014, 42(4): 476.

LI Jingpei, YUE Zhuwen, SHAO Wei,etal. Calculation of design lifetime of PHC pipe pile in marine environment[J]. Journal of the Chinese Ceramic Society, 2014, 42(4): 476.

[6]邵伟, 李镜培. 氯离子侵蚀钢筋混凝土管桩的使用寿命预测[J]. 同济大学学报：自然科学版, 2014, 42(12): 1820.

SHAO Wei, LI Jingpei. Service life prediction of reinforced concrete pipe pile due to chloride ion corrosion[J]. Journal of Tongji University：Natural Science, 2014, 42(12): 1820.

[7]Collepardi M, Marcialis A, Turrizzani R. The kinetics of penetration of chloride ions into the concrete[J]. II Cemento, 1970, 67(4): 157.

[8]Thomas M D A, Bamforth P B. Modelling chloride diffusion in concrete-effect of fly ash and slag [J]. Cement and Concrete Research, 1999, 29(4): 487.

[9]金伟良, 延永东, 王海龙. 氯离子在受荷混凝土内的传输研究进展[J]. 硅酸盐学报, 2010, 38(11): 2217.

JIN Weiliang, YAN Yongdong, WANG Hailong. Research progress On the chloride transportation in stressed concrete[J]. Journal of the Chinese Ceramic Society, 2010, 38(11): 2217.

[10]LU C H, WANG H L, JIN W L. Modeling the influence of stress level on chloride transport in pre-stressed concrete [C]∥ Proceedings of the international conference on durability of concrete structures. Hangzhou: [s.n.], 2008: 239-245.

[11]袁承斌, 张德峰, 刘荣桂, 等. 不同应力状态下混凝土抗氯离子侵蚀的研究[J]. 河海大学学报：自然科学版, 2003, 31(1): 50.

YUAN Chengbin, ZHANG Defeng, LIU Ronggui,etal. Diffusion of chloride in concrete in different stress states[J]. Journal of Hohai University: Natural Science, 2003, 31(1): 50.

[12]Konin A, Francois R, Arliguie G. Penetration of chlorides in relation to the micro cracking state into reinforced ordinary and high strength concrete [J]. Material Structure, 1998, 31(5): 310.

[13]Midgley H G, Illston J M. The penetration of chlorides into hardened cement pastes[J]. Cement and Concrete Research, 1984, 14(4): 546.

[14]Chen D, Mahadevan S, Chloride-included reinforcement corrosion and concrete cracking simulation[J]. Cement and Concrete Composite, 2008, 30(3): 227.

[15]Violetta B. Life-365 service life prediction model[J]. Concrete International, 2002, 24(12): 53.

[18]Francois R, Arligure G, Castel A. Influence of service cracking on service life of reinforced concrete [C]∥Concrete under severe conditions 2: environment and loading. London: Taylor & Francis, 1998, 143-152.

[19]Mohammed T U, Hamada H. Relationship between free chloride and total chloride contents in concrete[J]. Cement and Concrete Research, 2003, 33(9):1487.

[20]汪冬冬, 王成启, 石蓓玲, 等. 大管桩现场取样分析与耐久性研究[J]. 中国港湾建设, 2008(1): 39.

WANG Dongdong, WANG Chengqi, SHI Beiling,etal. Field sampling, analysis and search on durability of large diameter cylindrical pile[J]. China Harbour Engineering, 2008(1): 39.

[21]Enuelund S, Edvardsen C, Mohr L. General guidelines for durability design and redesign, curacreate: probabilistic performance based durability design of concrete structures [R]. [S.l.]: European Union, 2000.

Service Life Prediction Model of Concrete Square Piles in Marine Environment

LI Jingpei1,2, LI He1,2

(1. Key Laboratory of Geotechnical and Underground Engineering of the Ministry of Education, Tongji University, Shanghai 200092, China; 2. College of Civil Engineering, Tongji University, Shanghai 200092, China)

A diffusion equation of chloride ion in concrete was put forward based on Fick's second law. In the equation, the influences of time-dependence of chloride diffusivity, the effect of load on diffusion coefficient and chloride ion binding capacity of concrete were taken into consideration. A prediction model of service life of reinforced concrete (RC) square piles was established. The effects of cover thickness, cracking width, surface chloride ion concentration and the chloride threshold level on service life of RC square piles were analyzed. The analysis results indicate that the diffusion equation of chloride ion of this paper agrees well with the experimental data. It suggests that the cover thickness should be greater than 45 mm and the cracking width should not be greater than 0.1 mm if the design service life of RC square piles is 50 years.

durability of concrete; reinforced concrete square piles; chloride diffusion; service life

2015-05-18

国家自然科学基金(51178341)

李镜培(1963—)，男，工学博士，教授，博士生导师，主要研究方向为岩土力学及桩基础工程.E-mail: lijp2773@tongji.edu.cn

TU528

A