基于数值仿真与飞行试验的弹道修正火箭弹阻力系数简易辨识
郭庆伟,宋卫东,王 毅,卢志才
(军械工程学院火炮工程系,河北 石家庄 050003)
基于数值仿真与飞行试验的弹道修正火箭弹阻力系数简易辨识
郭庆伟,宋卫东,王毅,卢志才
(军械工程学院火炮工程系,河北 石家庄 050003)
作为单通道鸭舵控制弹道修正火箭弹研究的关键技术之一,气动系数的辨识是实现弹体飞行控制的前提与基础。该文以阻力系数简易辨识为主要研究内容,主要探讨数值仿真与飞行试验相结合对阻力系数进行辨识的方法。利用Grigen网格划分技术和Fluent流体力学仿真(CFD)相结合,获得弹道修正火箭弹的仿真气动数据;通过弹体的受力和力矩分析,建立六自由度弹道模型;根据飞行试验数据,对比分析弹道模型与仿真气动数据,对阻力系数进行修正优化。通过试验验证,经过修正的阻力系数精度得到很大提高,对于研究弹道修正弹的弹道特性规律和制导控制设计具有参考价值。
弹道修正火箭弹;数值仿真;飞行试验;系数辨识
0 引 言
随着世界形势的变化和武器装备的发展,战争形态发生了重大变化,准确打击成为重要的作战方向,制导弹药在现代战争中发挥着越来越重要的作用。我国制导弹药发展相对滞后,主战弹药大多数为传统无控弹药,如何在现实条件下提高精确打击能力成为当前重要的研究课题。弹道修正技术具有低成本、高准确度等优势,能够很好地与传统弹药改造相结合,是当前国内外研究的重要方向。瑞士厄利空·康特拉夫斯公司与德国莱茵金属公司联合研制了用于无控火箭弹改造的“增强型弹道修正”(CORECT)模块,CEP提高到50m以内[1]。美国科学家Pete Burke[2]在减旋理论的基础上对新型鸭舵控制方法和控制机构进行了大量的研究,提出XM1156 PGK灵巧引信,大大提高了炮弹的射击准确度。美国ATK公司研制生产新型迫击炮弹制导组件(MGK)也已进入装备应用阶段[3-4]。国内相关领域的研究尚处于起步阶段,以理论研究为主,如史金光等[5]开展了阻力环-阻尼片组合式二维弹道修正执行机构,余浩平、陈贺等[6-7]对双旋结构的弹道修正引信技术进行了理论研究。
火箭弹作为当前我国的主战弹药之一,亟需信息化改造,而基于单通道鸭舵控制的弹道修正技术成为其信息化改造的重要研究方向。作为单通道鸭舵控制弹道修正的关键技术,气动系数的辨识是实现弹体飞行控制的前提与基础,准确的气动系数可以为研究弹道特性、设计控制方案提供很好的技术支撑。
本文以气动系数辨识为主要研究方向,探讨以CFD数值仿真与飞行试验相结合的方法,运用Grigen网格划分、Fluent流体力学计算、C++程序仿真等工具,结合实际飞行试验数据,研究阻力特性的规律,对阻力系数进行辨识。
1 气动系数辨识
在飞行过程中,弹体的弹道特性、稳定性和控制规律等都受到空气动力的影响,而空气动力与力矩的研究可以通过气动系数表征。目前,对弹体气动力与力矩研究主要有理论计算、数值仿真、试验研究(主要包括风洞试验或飞行试验等)[8-12]3种方式。
随着空气动力学、飞行力学、数学理论等不断发展,可以通过理论计算对实际气动特性进行很好的描述,但是存在计算复杂、附加条件多、定量计算精度差等缺点[13-15],而且针对具体的环境特点存在不同程度的误差。随着计算机技术和仿真技术的迅速发展[16-18],数值仿真方法能够直观地对气动的特性进行描述,但是目前还是针对有限的模型和环境条件进行仿真。风洞试验能够很好地获得弹体静态流场特性,获取准确的气动力与力矩,但是存在费用昂贵、时间周期长、动态特性难以获取等缺点;飞行试验能够提供实际飞行状态,获取的数据能够反映实际受力与力矩的状态,综合反映不同影响因素,但是对试验数据的准确度要求高,对弹道模型和数据处理的方法也有很大的依赖[19]。
对比不同的气动系数研究方法的特点和优势,以阻力系数为研究对象,本文提出数值仿真和飞行试验相结合的阻力系数辨识新方法,首先利用数值仿真获取基础气动数据,并通过建立弹道修正火箭弹基本六自由度弹道模型对飞行试验弹道进行仿真,最后通过对比仿真弹道与试验飞行弹道,利用飞行试验数据对仿真阻力系数进行辨识与修正,优化阻力系数,提高阻力系数的准确性。
2 气动系数数值仿真
2.1仿真对象
单通道鸭舵控制的弹道修正火箭弹是低速旋转的尾翼火箭弹,一对同轴固联的舵片安装在弹体头部,舵片零度位置与弹体纵轴平行,如图1所示。通过电机控制舵片的偏转角度,改变其气动受力,从而产生控制力,对弹道进行修正实现制导控制。

图1 单通道鸭舵控制的弹道修正火箭弹示意图
2.2仿真内容
弹体在飞行过程中,受到空气动力的影响,其中阻力主要作用于飞行速度,进而对射程产生影响。对于单通道鸭舵控制的弹道修正火箭弹,其所受阻力主要由两部分组成,零升阻力和诱导阻力,相应的阻力系数也是由两部分组成,即:
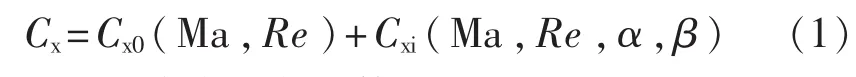
式中:Cx0——零升阻力系数;
Cxi——诱导阻力系数;
Ma——飞行马赫数;
Re——雷诺数;
α——弹体攻角;
β——弹体侧滑角。
对于单通道鸭舵控制弹道修正火箭弹,零升阻力系数与弹体的结构外形和布局、飞行速度、外界环境有关;诱导阻力主要是由于攻角产生的升力引起的,当侧滑角产生侧向力时也会引起相应的诱导阻力,因而诱导阻力系数主要与速度、攻角、侧滑角、外界环境有关。因此,为获取准确的仿真阻力系数需要对不同的马赫数(Ma)、攻角(α)、侧滑角(β)进行组合,对每一种情况进行仿真获取不同条件下的气动系数。同理,可获取弹体飞行过程中所受的其他力与力矩系数。
根据单通道鸭舵控制弹道修正火箭弹的气动特性和弹道特点,气动系数的变化具有一定的规律性,无需对速度进行大量采样,但是跨音速段气动系数变化相对较大,需要增大采样数据。本课题火箭弹飞行速度大部分时间处于超音速,因此选择弹体在马赫数为0.8,1.2,1.5,2.0,2.5,3.0,3.5下的气动系数进行仿真。由于火箭弹弹体处于飞行稳定状态时,攻角和侧滑角的变化很小,在10-1数量级,不过在起始段火箭弹飞行速度较低,受到干扰时可能产生较大的攻角变化,能够达到3°左右,角度变化范围很小,根据气动系数的特点,在攻角小角度范围内其变化呈线性,因此可以取少量的点进行线性插值即可,本文选取了攻角和侧滑角为0°、±2°、±4°对气动系数进行仿真。
2.3仿真建模
本文采用流体力学软件Fluent对单通道鸭舵控制弹道修正火箭弹进行数值仿真,首先通过Gridgen软件对弹体实体建模和网格划分,导入Fluent软件,选择求解器,本文选择耦合、隐式求解器;湍流模型采用Spalart-Allmaras方程湍流模型;设置远场压力边界条件;进行迭代计算求解。
为保证计算精度及计算速度,全部采用结构化网格(即六面体网格),贴近弹体壁面网格加密,第1层网格高度取0.01mm。图2、图3分别给出零舵偏时的全局及局部网格示意图。

图2 全局网格示意图

图3 局部网格示意图
2.4仿真结果
针对不同Ma、α、β下的气动系数进行仿真计算,其中阻力系数结果如图4所示。

图4 阻力系数仿真结果
可以看出,阻力系数曲线出现了两个极点,一个在1.2左右,另外一个在2.0左右,这与实际的弹体结构特点是一致的。如图5所示,由于弹体舵片具有一定的前缘后掠角,导致气体来流速度在舵片前缘线垂直方向的速度分量νw<实际速度ν,所以虽然来流速度ν的Ma在1.0左右,弹体主要部位已经产生了激波,阻力系数出现了极值点,但是作用在舵片上的速度分量νw还小于1.0,未满足激波产生条件,因此只有当速度分量νw>1.0时,舵片前缘才产生激波,故另一个极值点会向后移动,在Ma超过1.0后的某个位置产生第2个极值点。阻力曲线的特点与实际的弹体结构相符合,仿真结果可信、具有一定的准确度,但仍需要进一步的验证与修正。

图5 舵片来流速度
3 气动系数数值仿真
为了验证仿真计算气动参数的准确性,同时对弹道模型进行修正,需要对弹体进行靶场试验,由于经费、时间等方面的限制,试验弹的数量较少,无法获得大量数据。针对此种小样本情况,提出以试验数据修正仿真数据,以优化气动数据、提高准确度。
由于弹道模型的建立主要是对弹体的受力与力矩进行分析,本文基于单通道鸭舵控制弹道修正火箭弹的弹体特点给出了六自由度弹道模型,并以此模型建立仿真模型,根据实际的试验环境输入条件,对飞行弹道进行仿真。通过对比仿真弹道与实际飞行弹道数据,对气动数据进行修正,得到更加准确的气动数据,为后续控制方案的设计和改进提供帮助。
3.1六自由度弹道模型
根据单通道鸭舵控制弹道修正火箭弹的特点,为了描述弹体在飞行过程中的弹道特点,建立六自由度弹道模型。弹体在飞行过程中受到的力有发动机推力、气动力、重力等,受到的力矩主要有气动力矩、阻尼力矩等。由于鸭舵修正采用的气动力控制,控制力为气动力的增量变化,与弹体的气动受力耦合交叉,因此不再区分单独的控制力与力矩。本文对弹道模型的建立仅作了简单的描述,不做具体详细的研究分析。
坐标系的建立和符号的定义见文献[20],在准弹体系下弹体受到的力与力矩有:推力、阻力、升力、侧向力、俯仰力矩、偏航力矩、滚转力矩以及各向阻尼力矩,将准弹体系受力转化到发射惯性系,有发射系下弹体质心运动方程为

式中:Fx、Fy、Fz——发动机推力在发射系下的分量;
Rx、Ry、Rz——空气动力在在发射系下的分量,也就是阻力、升力、侧向力由准弹体系坐标转换到发射系下的分量;
gx、gy、gz——重力在发射系下的分量;由于射程较近,地表面近似平面,忽略科氏加速度和牵连加速度。
为了描述弹体的绕质心运动,在准弹体系下弹体受到的力矩主要有:俯仰力矩、偏航力矩、滚转力矩和对应的阻尼力矩,建立绕质心动力学方程为
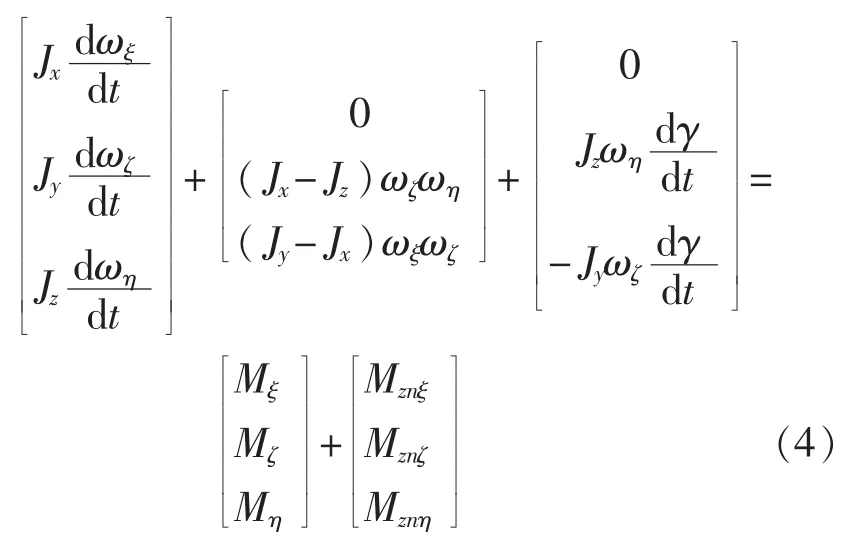
式中:Jx、Jy、Jz——转动惯量在准弹体坐标系下的分量;
ωξ、ωζ、ωη——弹体滚转角速度在准弹体系下的分量;
Mξ、Mζ、Mη、Mznξ、Mznζ、Mznη——俯仰力矩、偏航力矩、滚转力矩及其对应的阻尼力矩在准弹体系下的分量;
γ——弹体滚转角。
根据角度的转换关系,有姿态角速度与弹体转速的关系方程为

式中:φ——弹体俯仰角;
ψ——弹体偏航角。
依据上述弹道模型利用VC++软件编写仿真程序,采用4阶龙格-库塔法对上述弹道方程进行积分数值计算。在仿真弹道模型中,气动力与力矩利用仿真所得的气动系数通过线性插值获得。
3.2系数修正方法
通过弹道模型可知,除了气象条件外,影响射程的主要因素就是阻力系数的大小,因此可以通过仿真弹道与实际飞行弹道的拟合程度判断系数的准确程度,反之利用两者的拟合程度对系数进行修正,这是本文重点研究的内容。由于火箭弹特殊的弹道特性,主动段与被动段的阻力系数是不同的,由于主动段受到发动机燃气的影响,弹体受到的底阻减小,阻力系数也就减小,因此,对于火箭弹而言,必须以主动段和被动段分开进行。
首先,对主动段和被动段所受阻力的特点进行分析:
1)主动段的阻力系数对射程的影响。通过改变弹体受力产生加速度,对关机点最大速度产生影响,进而改变被动段弹道,因此主动段的阻力系数修正的主要目的在于拟合最大速度。
2)主动段相对于整体的飞行弹道来说,作用时间短、过程复杂、速度增加快、弹道平直,由于阻力对弹道的影响是时间累积的过程,需要时间达到作用的效果,对于主动段,马赫数变化较大,单一马赫数范围内,如2.5~3.0Ma范围的时间仅为0.4s,时间很短,此区间内阻力大小对整个主动段的影响较小,因此对于整个主动段而言,阻力系数的精度可以适当降低。
3)主动段与被动段的阻力产生的原理不同,但是两部分共同的主要影响因素是弹体的结构外形,考虑发动机稳定工作时对阻力系数带来的影响也是稳定的,因此阻力系数的变化可以认为主要由弹体结构外形变化所致。
通过上述分析,本文以被动段阻力系数为基础,近似认为主动段阻力系数是被动段阻力系数的倍数,以此假设为基础,简化阻力系数的优化过程。由于主动段阻力系数作用时间短,主要通过最大速度对被动段弹道产生影响,因此在保证最大速度拟合的基础上做出上述近似处理是可行的。
综上可知,阻力系数的修正与优化主要集中在被动段,主动段的阻力系数以被动段系数为基础乘以相应的系数,而被动段阻力系数以仿真阻力系数为初始值,不断通过拟合被动段弹道实现修正与优化,具体阻力系数修正过程如图6所示。

图6 阻力系数修正流程图
3.3阻力系数的修正
在我国西北某靶场对无控状态弹道修正火箭弹开展了自由飞行试验,设定射角为45°,可获得试验雷测数据。利用建立的弹道模型和仿真气动数据,结合实测气象数据,对弹体飞行弹道进行仿真获得仿真弹道,对比仿真弹道和雷测弹道特性如图7、图8所示。从图可知,仿真弹道与雷测弹道有较大的偏差,发动机关机点速度偏差为0.06Ma(约20m/s),弹道高偏差为1200m,落点射程偏差2400m。由于雷达测量的准确度较高,误差相对较小,分析偏差产生的主要原因为气动系数的影响。

图7 速度对比曲线

图8 弹道高曲线对比
按3.2所述,将弹道的主动段和被动段分开进行拟合:
1)主动段以拟合关机点速度为主,为了拟合关机点最大速度,利用修正系数Ki(i=1,2,3,…)对被动段阻力系数进行处理获得主动段阻力系数。
2)被动段主要进行弹道高拟合,由图7雷测速度曲线所示,从被动段到落点飞行速度是单调减小的,在最后落点处略有增加,但是整个飞行弹道速度的变化没有重复的区间。仿真阻力系数在不同马赫数下与上述弹道区间可以一一对应,因此,对于被动段而言,可以按照速度大小划分为不同的弹道区间(AB、BC、CD、DE、EF),每个弹道区间对应特定马赫数下的阻力系数,从而建立起弹道与阻力系数的对应关系——特定的阻力系数对应特定的弹道区间,具体对应关系如表1所示。

表1 弹道区间划分
对于被动段阻力系数的修正,按照弹道区间逐一进行弹道高的拟合,从AB段到EF段,每一段修正完成后,都会对主动段产生影响,需要对修正系数进行更新,最终实现被动段的完整拟合。实际拟合过程中的弹道变化曲线如图9所示。
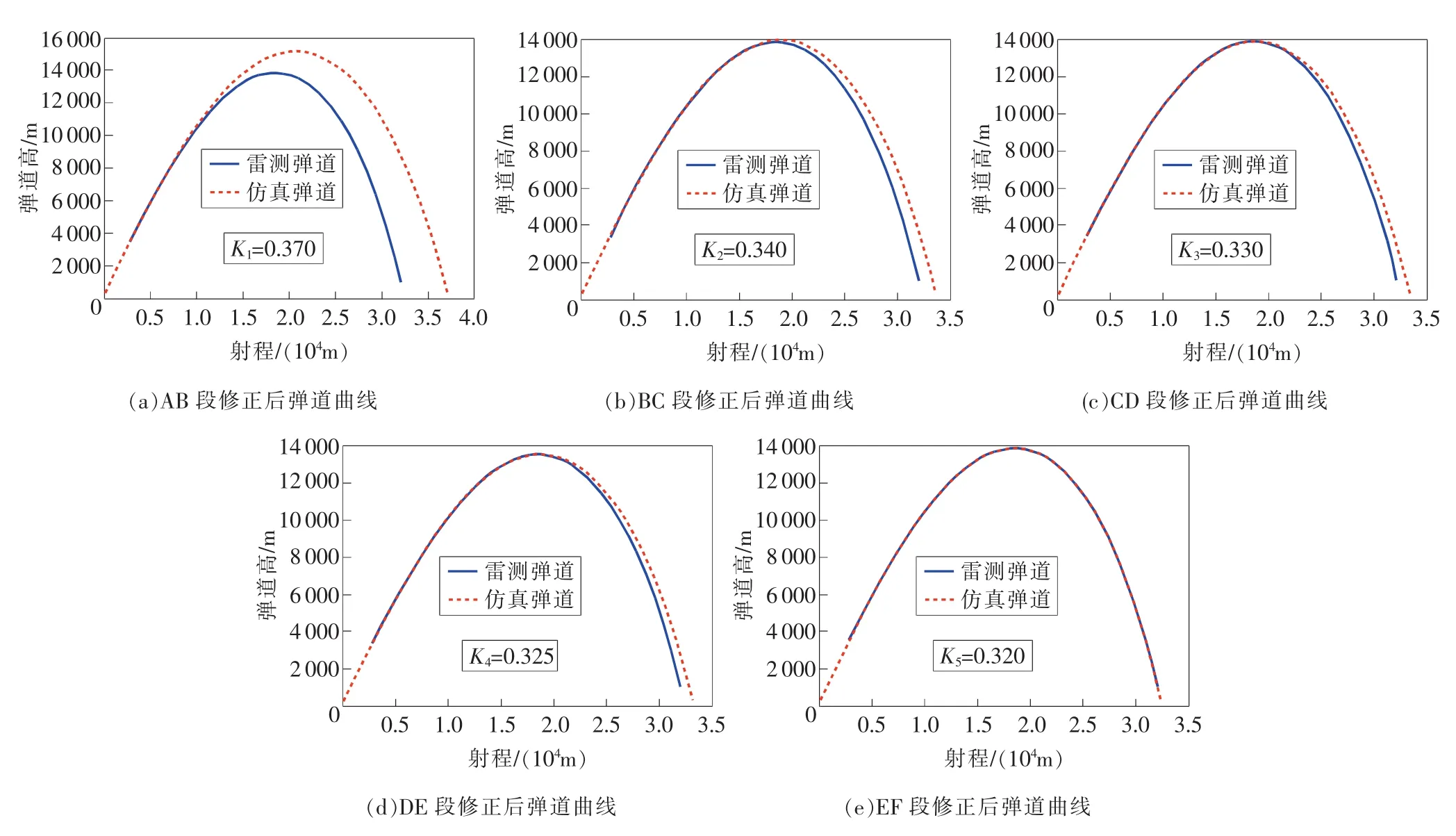
图9 系数修正过程弹道高曲线变化
通过对比图9中(a)~(e)所示弹道高曲线的变化可知,随着修正区间的不断增加,阻力系数的准确度不断提高,仿真弹道与实际雷测弹道的偏差明显减小。最终的修正结果显示,整个飞行过程中,弹道高的偏差在20m以内,落点射程偏差49 m,从而使仿真阻力系数的精度得到较大的提高。
为了进一步提高阻力系数修正的准确性和一致性,可以对多发试验弹采用上述的方法步骤分别进行阻力系数的修正,然后对系数取平均值,能够减小修正误差,提高优化的效果。
4 试验验证
为了对修正后的数据进行验证分析,选用新的试验弹道分别以20°和40°射角进行靶场自由飞行试验。利用修正后阻力系数,根据实际气象条件,对比雷测弹道曲线与仿真弹道曲线,如图10、图11所示。
如图所示,以20°和40°射角进行试验,对应了不同弹道状态下的阻力系数的适应性。根据对比结果可知,20°射角下雷测与仿真弹道高的偏差最大为40 m左右,射程偏差60 m;40°射角下雷测与仿真弹道高的偏差最大为60m左右,射程偏差80m。
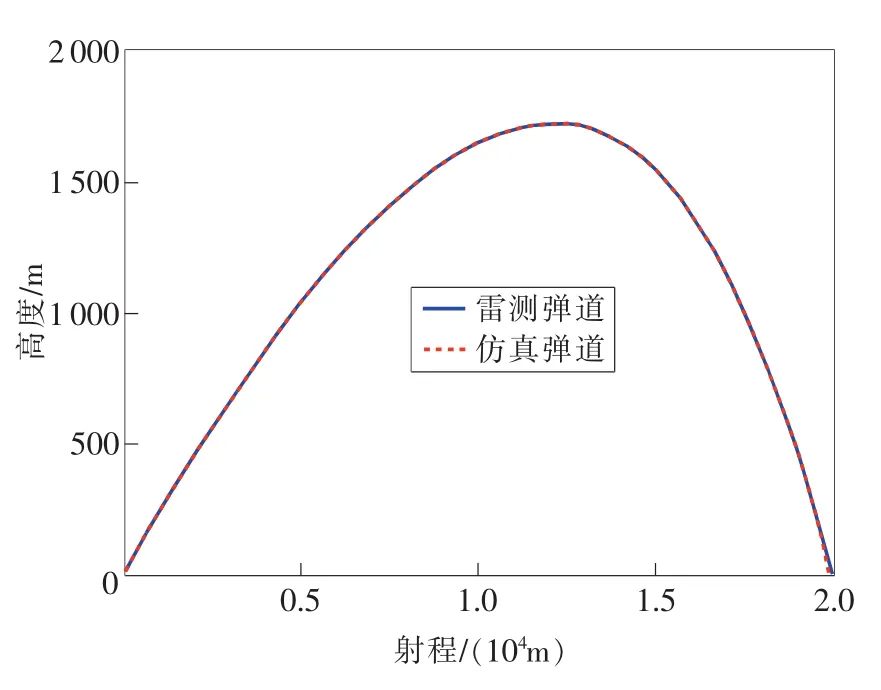
图10 20°射角弹道高曲线对比

图11 40°射角弹道高曲线对比
验证试验的结果可以得出,结合数值仿真和小样本飞行试验得出的阻力系数,能够达到较高的准确度,具有良好的适应性,可以作为前期的方案设计和弹道特性研究的重要手段。
5 结束语
本文利用CFD数值仿真与飞行试验相结合的方法对弹道修正火箭弹的阻力系数进行辨识,相比理论计算、试验等方法,原理简单易行、成本降低、时间周期短,具有很好的现实应用价值。本文阐述了具体的阻力系数的辨识方法和过程,利用Fluent、Grigen等流体力学软件获得仿真气动数据,并通过实际飞行试验的验证,具有良好的辨识精度。但是,本方法适用于阻力系数的简易辨识,精度需要进一步提高,可通过加大试验样本量,通过统计学与本方法相结合提升系数优化的精度,为下一步的制导控制设计和弹道分析提供有利支撑。
[1]GAMBLE A E,JENKINS P N.Low cost guidance for the multiple launch rocket system(MLRS)artillery rocket[R].IEEE PLANS on Position Location and Navigation Symposium,2000:193-199.
[2]PETE B.XM1156 Precision Guidance Kit(PGK)[C]∥NDIA 52nd Annual Fuze Conference,2008.
[3]TOMB.Precision Guidance Kit[C]∥45th Annual NDIA Gun and Missile Systems Conference,2010.
[4]KELLY H.Mortar Guidance Kit(MGK)[C]∥2010 Joint Armaments Conference,2010.
[5]史金光,王中原,常思江,等.二维弹道修正弹修正方法[J].海军工程大学学报,2010,22(4):87-92.
[6]余浩平,杨树兴.一种新型弹体结构导弹动力学方程的建立[J].弹箭与制导学报,2003,23(3):153-155.
[7]陈贺.修正控制技术与飞行稳定性研究[D].沈阳:沈阳理工大学,2013.
[8]王欣,郝永平,张凤阁,等.弹道修正引信阻力系数辨识方法研究[J].微计算机信息,2009,25(7):199-200.
[9]WEISSS.Identificationofnonlinearaerodynamic derivatives using classical and extended local model networks[J].Aerospace Science and Technology,2010,42(1):1-12.
[10]单长胜.从弹箭自由飞行数据提取气动力系数的方法研究[D].南京:南京理工大学,2001.
[11]纪楚群.导弹空气动力学[M].北京:宇航出版社,1996:79-83.
[12]吴日恒,郭泽荣,李世义.射程修正引信弹道辨识方法及精度分析[J].弹道学报,2008,20(1):43-47.
[13]王贵东,崔尔杰,刘子强.闭环气动参数辨识的两步方法[J].飞行力学,2010,28(2):16-19.
[14]孙勇,段广仁,张卯瑞,等.高超声速飞行器再入过程改进气动系数模型 [J].系统工程与电子技术,2011,33(1):134-137.
[15]李晓斌,董敬文,王永杰,等.火箭靶弹零升阻力系数辨识[J].固体火箭技术,2010,33(1):5-8.
[16]梁明.靶弹动力学模型参数辨识与弹道仿真[J].战术导弹技术,2012(3):48-53.
[17]张英,刘创,杨小会,等.基于有限体积法的弹丸阻力系数数值模拟方法[J].探测与控制学报,2013,35(4):27-31.
[18]曹松棣,田野,郭全,等.应用Fluent软件获取导弹气动系数[J].飞行仿真,2007(3):24-27.
[19]刘述.弹箭飞行数据气动力参数辨识分析[D].太原:中北大学,2013.
[20]韩子鹏.弹箭外弹道学[M].北京:北京理工大学出版社,2008:121-124.
(编辑:李妮)
Drag coefficient identification of trajectory corrected rockets based on numerical simulation and flight test
GUO Qingwei,SONG Weidong,WANG Yi,LU Zhicai
(Department of Artillery Engineering,Ordnance Engineering College,Shijiazhuang 050003,China)
As the critical technology of the canard-corrected rocket in single channel control,aerodynamic parameters identification is the foundation and precondition for projectile guidance. This paper focuses on drag coefficient identification and mainly involves the method of the incorporationbetweennumericalsimulationandflighttest.WiththecontributionofGrigen gridding division technology and Fluent fluid dynamic simulation,the emulation aerodynamic parameters has been conducted.From analysis of forces and moments acting on the projectile,the six degrees of freedom dynamic model was given.The flight test data has be used to make a comparison of fight data and the simulation data and provides the optimization proposal for the drag coefficient.In the end,the demonstration tests indicate that the optimized drag coefficient has a better precision that could be provide significant reference for the projectile trajectory characteristics and the guidance law design.
trajectory corrected rocket;numerical simulation;flight test;coefficient identification
A
1674-5124(2016)06-0127-07
10.11857/j.issn.1674-5124.2016.06.027
2015-12-23;
2016-02-13
中国博士后科学基金(2013M542454)十二五装备预先研究项目(9140A05040114JB34015)
郭庆伟(1988-),男,山东东平县人,博士,专业方向为弹箭外弹道理论与应用。

