软岩声发射序列分形特征研究

沈　忠，付小敏，黄兴建，张　昕，宾婷婷

（成都理工大学 地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059）

软岩声发射序列分形特征研究

沈忠，付小敏，黄兴建，张昕，宾婷婷

（成都理工大学 地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059）

为研究软岩声发射序列的分形特征，在MTS815程控伺服刚性试验机上，对膏质泥岩、粉砂岩、页岩进行单轴压缩下的声发射试验。结果表明：声发射序列分形是有限度的，超过一定限度不再分形；随相空间维数m的增加，双对数图整体下移且无标度区变窄，同时关联维数D呈现出增加-稳定-发散的发展过程；3类岩石均在应力水平40%～50%时，关联维数D值最大，随后声发射活动在主破裂附近产生丛集现象，关联维数降低至较低水平；声发射分形维数的演化表现为“波动-上升-有起伏的整体下降”链式模式，同时得出损伤破裂的分形识别模式为“峰值-第2波峰”模式或称“反对号（）”模式。据此为岩体稳定性监测提供一种新的识别方法。

声发射；振铃计数率；分形；相空间维数；关联维数

0　引　言

岩石是一个天然的复杂地质体，在荷载作用下产生缺陷的闭合、生长乃至贯穿破坏。伴随此过程的发展诱发能量以弹性波的形式释放，即声发射现象。岩石声发射现象蕴含着岩石整个破裂过程的大量信息，量化声发射参数的统计信息是度量岩石材料和力学结构稳定性的有效途径之一。

分形理论［1］于20世纪70年代中期正式诞生，其揭示了非线性系统中有序与无序的统一，确定性与随机性的统一，使人们探索极为复杂现象背后所存在的规律性成为可能［2］。定量描述分形的参数是分形维数，其测定方法包括：Hausdorff维数，容量维数，盒维数，信息维数，关联维数等。20世纪80年代分形理论得到快速发展，谢和平［3］院士创造性地将损伤力学和分形几何相联系，开辟了岩石损伤断裂的分形几何新领域。而今，运用分形理论来研究岩石声发射动力系统已成为新的课题。岩石在受力破裂过程中所产生的声发射序列在时间和空间分布上均具有分形特征［4］。一些学者运用不同分维测定方法验证岩石声发射在空间上是分形的［5-7］。吴贤振等［8］研究了不同岩石破裂全过程的声发射序列分形特征；梁忠雨等［9］研究了单轴压缩下岩石声发射的分形特征；高保彬等［10］研究了同组软煤岩的声发射分形特性；刘延保等［11］研究了含瓦斯煤体单轴和三轴压缩下AE序列关联维数演变过程。尹贤刚等［12-13］研究了岩石声发射强度分形以及平静期附近的分形特点；纪洪广等［14］研究了混凝土材料三点弯曲过程的声发射分形特征；张黎明等［15］研究了卸围压下大理岩声发射振铃计数率序列的分形特征。

上述分形研究大多基于坚硬岩石展开，对于柔软岩石却鲜有报道。在工程中，岩体稳定性监测的岩性各异，尤其是软弱区最易引发地质问题，因此寻找切实有效的岩体稳定性监测识别模式具有重要意义。分形理论是研究非线性系统的有效工具且与基本的声发射参数相比，分形维数具有更好的稳定性和直观性［14］，据此本文运用分形理论对3类软岩声发射序列进行研究，旨在为岩体的稳定性监测提供有效依据。

1　岩石声发射试验

1.1岩石试样的制备

本试验采用的3组试样分别为膏质泥岩、粉砂岩、页岩。试验样品严格按照现行规范加工为长方体，其平整度、平行度和垂直度皆满足试验要求。岩样信息如表1所示。

表1　岩石试样的基本信息

1.2试验设备与试验方法

本次声发射试验由两套设备配合完成，加载设备为MTS815刚性试验机，框架整体刚度5000kN/mm，最大轴压300t，应变率适用范围10-2～10-7s-1。考虑噪音对声发射参数的影响，采用单轴压缩试验。加载方式首先采用荷载控制，速率10kN/min，荷载达10 kN之后转换为位移控制，速率为0.1mm/min，直至试验结束。监测设备采用声华公司生产的SAEU2S声发射系统，对整个试验过程进行全程跟踪，设置采样频率2 500 kHz，采样长度（点数）2044，参数间隔500 μs，外参（荷载）采集间隔1s，前置放大器增益值为40dB。试样端部粘贴医用胶带消除端部及外部传递的噪音影响，声发射探头用凡士林耦合安放在试样的中央，并用橡胶圈固定。

1.3试验结果

MTS815试验机数据采集时间、荷载和位移，得到3组岩样的单轴抗压强度，如表1所示。声发射监测设备数据采集时间、幅度、振铃计数、能量和荷载5个参数。图1为岩样SY-1声发射振铃计数及其累计计数监测图。

图1　声发射监测图

2　岩石声发射分形特征分析

岩石声发射振铃计数率与岩石内部颗粒位错，夹杂物和矿物结晶体断裂及裂纹扩展所释放的应变能成比例［15］，能全面反映岩石内部物理力学性质的变化。关联维数可实现一维数据研究多维空间，为处理声发射数据序列提供了一种新方法。据此，本文采用声发射振铃计数率作为研究序列，运用关联维数对3类软岩在时域上的分形特征进行分析。

2.1G-P算法计算关联维数

Takens指出系统中任一分量的演化都是由与之相互作用的其他分量决定的，因此这些相关分量的信息就隐藏在任一分量的发展过程中。1983年Grassberger和Procaccia根据嵌入理论和重构相空间思想提出了从时间序列直接计算关联维数D的算法，即G-P算法。

将声发射过程基本参数振铃计数率序列作为研究对象，则振铃计数率序列可对应一个容量为n的序列集｛x1，x2，…，xn｝，并可用这些数据支起一个m维相空间。首先取前m个数据x1，x2，…，xm，由它们在m维空间中确定出第1个相点，记为X1。然后去掉x1，再依次取m个数据x2，x3，…，xm+1，由这组数据在m维空间中构成第2个相点，记为X2。如此依次可以构造N个（N=n-m+1）相点，则关联函数：

如果存在C（r）∝rD，则关联维数为

r0是相空间Rm中吸引子上相点距离的平均值。在不同的系数k下，每一个给定的尺度r对应一个C（r）值，C（r）实质是相点距离不大于尺度r的概率。在双对数坐标下对点（r，C（r））进行一次线性回归。若存在相关性，则回归线的斜率即为声发射序列的关联维数D。

2.2相空间维数m的取值分析

本文采用几何不变量法［16］来确定相空间维数。逐渐增加相空间维数m，取直到吸引子的几何不变量（分形维数、Lyapunov指数）不再变化为止的维数值，然后根据Takens定理（嵌入维至少是吸引子维数的2倍，即m≥2d+1）检验其有效性。在Matlab环境下编译计算程序，相空间维数m分别取2，4，…，20，在给定的600个尺度下，计算关联函数C（r）的值。图2为岩样SY-1尺度r和关联函数C（r）双对数散点图。

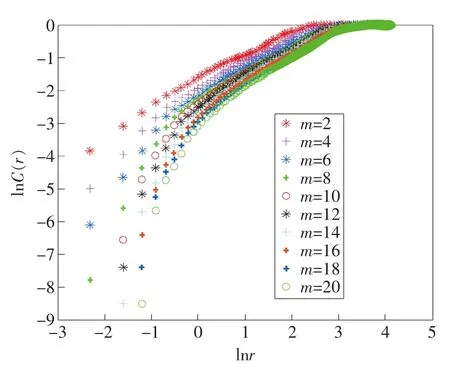
图2　不同相空间维数m下r-C（r）双对数散点图

当尺度r过小时，C（r）分布分散无分形现象；当尺度r取值适当，r和C（r）在双对数坐标下呈一次线性排列；当尺度r大于相空间Rm上任意两相点之间的距离时，关联函数C（r）=1，亦无分形现象，所以图形线型区是有范围的，也即岩石声发射序列分形是有限度的，超过一定的限度便不再分形，此范围也称为无标度区。当尺度r一定时，相空间维数m的增加导致相点距离增加，从而关联函数C（r）下降，图形呈现下移的趋势。在尺度r很小时，随相空间维数m的增加，图形向下弯曲导致无标度区变窄。因此随相空间维数m的增加，尺度r和关联函数C（r）双对数图整体下移且无标度区变窄。图2无标度区一次线性回归得到相空间维数m和关联维数D的关系曲线如图3所示。

图3　相空间维数m与关联维数D关系曲线

图4　关联维数拟合曲线

当相空间维数m较小时，关联维数随m的增大而增大，且逐渐趋于稳定；当m在6与14之间时，关联维数几乎没有变化，即吸引子的几何不变量不再发生变化；当m大于14之后，关联维数随m的增加而快速增加，关联维数D呈发散趋势。关联维数D随相空间维数m的增加经历增加-稳定-发散的过程。限于篇幅，本节仅对岩样SY-1进行详细分析，但绝大多数岩样也具有相同的结论。由此可见，相空间维数m的取值对关联维数D有一定影响，所以在计算不同岩样声发射振铃计数率序列关联维数时应采用相同的m值。因此，综合考虑吸引子的几何不变量不再发生变化，Takens定理以及无标度区尽量宽阔，分形特征明显等因素，本文三类岩石取相同的相空间维数m=6。

2.3不同应力水平下岩石的分形特征

岩石声发射振铃计数率序列的实质是岩石损伤过程在时域上的统计序列，它与岩石内部的损伤演化规律一致，因而根据声发射振铃计数率序列计算关联维数D可以很好地反映岩石损伤破裂的整个演化过程。图4为3类岩石的单个岩样NY-2、SY-1、YY-2在相对应力水平（当前应力与峰值应力的比值）为40%时的关联维数拟合曲线。

岩样NY-2、SY-1、YY-2的线性回归相关系数r都在0.97以上，可见岩石声发射振铃计数率序列是分形的，具有统计自相似性。相关系数越高，自相似性越高，分形越明显。以时间为桥梁，在Matlab环境下建立相对应力水平（以下称应力水平）与关联维数D的关系，并运用样条差值绘制关联维数D的变化趋势线。图5展示了3个岩样NY-2、SY-1、YY-2在加载过程中关联维数的演化过程。

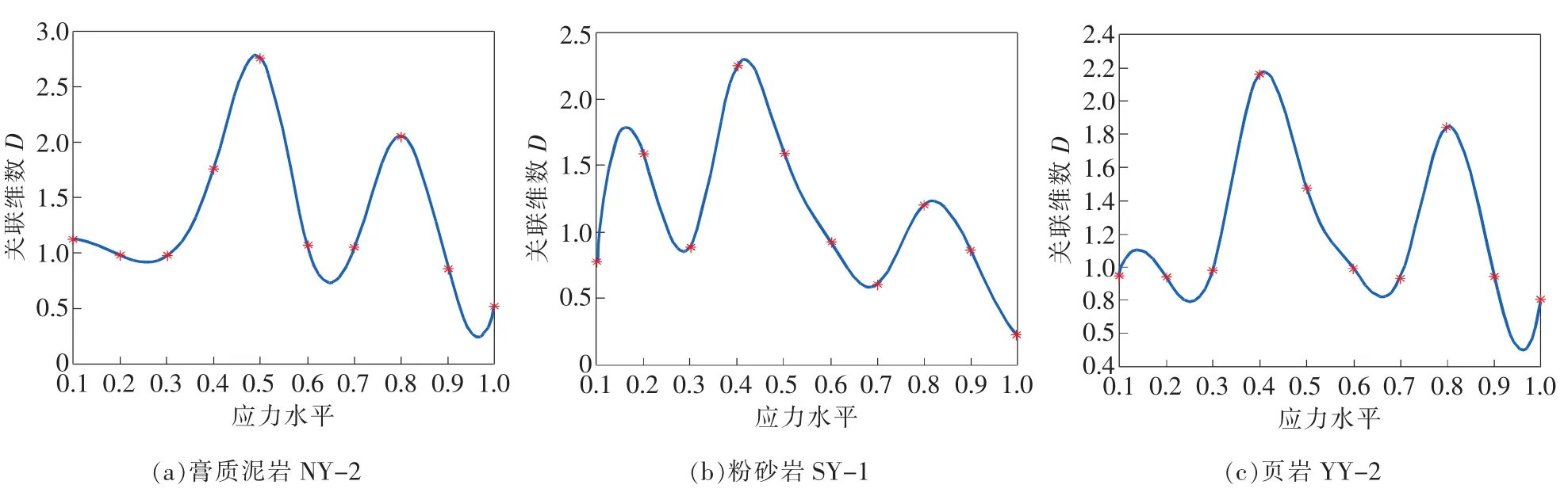
图5　不同应力水平下关联维数D的变化曲线

岩石损伤破裂过程中关联维数D不断变化，显示出不同的自相似程度。在不同应力水平下岩样关联维数D统计如表2所示。3类岩石在加载初期均显示出一定程度的波动现象，初步认为是加载初期岩石晶粒错动重新排列，微裂隙闭合以及加载初期声发射序列数据量偏小等综合作用的结果。随着荷载的增加，岩样的微裂隙均匀、稳定地扩展，此时关联维数D逐渐增大。当应力水平在40%～50%时，关联维数D值最大，此3类岩石表现出高度的一致性。随荷载的继续增加，裂隙开始相互连接、贯穿，岩石损伤破裂开始从无序向某一宏观有序发展，从整体向局部集聚发展，声发射活动在主破裂附近产生丛集现象，关联维数降低至较低水平。在此过程中，关联维数D相应呈现出有起伏的整体下降趋势。此3类岩石关联维数的最小值分布则较为分散，其原因有待进一步探讨。

表2　不同应力水平下关联维数D统计表

吴贤振等［8］总结出变粒岩、花岗岩等岩石破裂全过程声发射频率和能率序列分维值的演化模式为“波动-持续下降”模式，显然此演化模式在本文探讨的3类岩石上并不是非常适用。由图5及表2可以总结出此3类岩石的演化模式应为“波动-上升-有起伏的整体下降”模式。混凝土材料在临界断裂状态下，声发射参数的关联维数所表现出来的识别特征为“最大-最小”模式［14］。根据其他学者以及本文的研究，笔者认为“最大-最小”模式是真实存在的；然而，“最小”的分布过于分散且部分已接近破坏的临界点，作为事后验证是有效的，但在工程监测中运用存在风险。而将声发射参数分形维数的持续下降作为某一岩体失稳事件的前兆［8，12］难以准确判断识别点且运用上仍有很大安全储备。本文研究的3类岩石在分形维数D峰值之后，分形维数有起伏的整体下降会出现第2个波峰，甚至可能出现第3、第4个波峰，且第2波峰主要分布在应力水平为70%～80%之间，将此峰值作为岩体监测预报的特征识别点是有效可行的。此岩体稳定性监测的损伤破裂分形识别模式可定义为“峰值-第2波峰”模式或称“反对号（）”模式。

3　结束语

通过对3类岩石声发射振铃计数率序列的计算与分形分析，总结出以下结论：

1）岩石声发射序列分形有一定范围，超越这个范围不再分形。

2）相空间维数m的增加将导致尺度r和关联函数C（r）双对数图整体下移且无标度区变窄，同时关联维数D呈现出增加-稳定-发散的发展过程。综合考虑吸引子的几何不变量不再发生变化，Takens定理以及无标度区尽量宽阔，分形特征明显等因素，本文3类岩石取相同的相空间维数m=6。

3）膏质泥岩、粉砂岩、页岩均在应力水平40%～50%时，关联维数D值最大。随荷载的继续增加，裂隙开始相互连接、贯穿，岩石损伤破裂开始从无序向某一宏观有序发展，从整体向局部集聚发展，声发射活动在主破裂附近产生丛集现象，关联维数降低至较低水平。

4）膏质泥岩、粉砂岩、页岩的声发射分形维数演化模式为 “波动-上升-有起伏的整体下降”链式模式；损伤破裂的分形识别模式为“峰值-第二波峰”模式或称“反对号（）”模式。

［1］MANDELBROT B B.Fractals:forms Chance and dimension［M］.San Francisco：W.H.Freeman，1977：47-53.

［2］张济忠.分形-1995［M］.北京：清华大学出版社，1995：4-6.

［3］谢和平.分形-岩石力学导论［M］.北京：科学出版社，1996：101-106.

［4］MAYSTRE D，ROSSIJ P.Implementation of a rigorous vector theory of speckle for two-dimensionalmicroroughsurface［J］.J Opt Soc Am A，1986（3）：1276-1282.

［5］KUSUNOSE K，LEI X L，NISHIZAWA O，et al.Effect of grain size on fractal structure of acousticemissionhypocenterdistributioningranitic rock［J］.Physicsofthe Earthand Planetary Interiors，1991，67（1-2）：194-199.

［6］裴建良，刘建锋，张茹，等.单轴压缩条件下花岗岩声发射事件空间分布的分维特征研究［J］.四川大学学报（工程科学版），2010，42（6）：51-55.

［7］李元辉，刘建坡，赵兴东，等.岩石破裂过程中的声发射b值及分形特征研究［J］.岩土力学，2009，30（9）：2559-2563.

［8］吴贤振，刘祥鑫，梁正召，等.不同岩石破裂全过程的声发射序列分形特征试验研究［J］.岩土力学，2012，33（12）：3561-3569.

［9］梁忠雨，高峰，蔺金太，等.单轴下岩石声发射参数的分形特征［J］.力学与实践，2009，31（1）：43-46.

［10］高保彬，李回贵，李林，等.同组软硬煤煤样声发射及分形特征研究［J］.岩石力学与工程学报，2014，33（增2）：3348-3504.

［11］刘延保，曹树刚，李勇，等.含瓦斯煤体破坏过程中AE序列关联维数演化分析［J］.重庆大学学报，2012，35（3）：108-114.

［12］尹贤刚，李庶林，唐海燕.岩石破坏声发射强度分形特征研究［J］.岩石力学与工程学报，2005，24（19）：3512-3516.

［13］尹贤刚，李庶林，唐海燕，等.岩石破坏声发射平静期及其分形特征研究 ［J］.岩石力学与工程学报，2009，28（2）：3383-3390.

［14］纪洪广，王基才，单晓云，等.混凝土材料声发射过程分形特征及其在断裂分析中的应用［J］.岩石力学与工程学报，2001，20（6）：801-804.

［15］张黎明，任明远，马绍琼，等.大理岩卸围压破坏全过程的声发射及分形特征［J］.岩石力学与工程学报，2015，34（增1）：2862-2867.

［16］张雨，任成龙.确定重构相空间维数的方法［J］.国防科技大学学报，2005，27（6）：101-105.

（编辑：李妮）

Study on the fractal characteristics of acoustic emission sequence of soft rock

SHEN Zhong，FU Xiaomin，HUANG Xingjian，ZHANG Xin，BIN Tingting
（State Key Laboratory of Geohazard Prevention and Geoenvironment Protection，Chengdu University of Technology，Chengdu 610059，China）

In order to study on the fractal characteristics of acoustic emission（AE）sequence of soft rock，AE test of the gypsum mudstone，fine sandstone and shale was carried out in the MTS815 programmable servo rigidity testing machine under uniaxial compression.The results show that the fractal of AE sequence is limited，and exceeding a certain limit is no longer a fractal；with the increase of phase space dimension（m），double logarithmic diagram move down，scale-free zone is narrowed and the correlation dimension（D）shows the development process of increasestabilization-dispersion at the meantime；when three types of rocks are in the stress level of 40%-50%，the correlation dimension（D）is the biggest，and then the AE produce has the cluster phenomenon near the main rupture and the correlation dimension reduces to a low level；the evolution of AE fractal dimension is volatility-rose-decline with fluctuations and fractal recognition

acoustic emission；ringing counts rate；fractal；phase space dimension；correlation dimension

A

1674-5124（2016）06-0009-05

10.11857/j.issn.1674-5124.2016.06.003

2015-12-20；

2016-01-28

国家自然科学基金项目（41272321）

沈忠（1990-），男，湖北襄阳市人，硕士研究生，专业方向为岩土工程。

付小敏（1963-），女，四川绵阳市人，研究员，主要从事岩石室内试验相关工作。

pattern of damage and destruction is“peak to the second peak”mode or called“against ture（）”mode.This provides a new recognition method for monitoring the stability of rock mass.