基于图像处理的铁路货车交叉杆平面度检测算法研究

王燕燕，鲁五一，郑聪敏

（1.湖南机电职业技术学院电气工程学院，长沙 410151；2.中南大学 信息科学与工程学院，长沙 410075）

计算计算法

基于图像处理的铁路货车交叉杆平面度检测算法研究

王燕燕1，鲁五一2，郑聪敏2

（1.湖南机电职业技术学院电气工程学院，长沙 410151；2.中南大学 信息科学与工程学院，长沙 410075）

以OpenCV为软件开发平台，设计了一种基于数字图像处理的货车交叉杆平面度检测算法。首先利用局部对比度增强、背景差分对图像进行预处理突出被检测目标，然后对预处理后的图像采用自适应阈值改进了的Sobel算法提取目标边缘，利用局部图像截取感兴趣的图像部分，再利用最小二乘法来拟合圆形边缘得到圆心图像坐标，最后通过坐标变换和平面度计算公式实现相关参数的检测。分析实验结果表明该检测方法在实际应用中能取代人工目测，且满足实时性和高精度要求（精度±0.1mm，数据可靠性，即重复性测量标准差＜0.065mm），提升了工作效率和经济效益。

交叉杆；平面度；图像处理；坐标变换

0　引言

随着科学技术的不断进步，高速化、重载化的铁路货运对机车车辆的性能要求越来越高，这不仅需要提升货运车辆的相关技术，而且需要提升对货运车辆的检修质量和效率。而转向架作为车辆检修的一个重要部件，其检修的质量直接影响到了铁路货车的整体运行性能，交叉杆是转向架的主要构成部件之一，其对角线长度约有2200mm，属于大尺寸零件。目前对于交叉杆的相关几何参数的检测，主要采用特制标准尺人工去贴靠零件和人眼观察的方式，大体上判断交叉杆合格与否。显然这种人工检测方法需要多人共同协作才能完成，不仅费时费力，而且存在较大误差。低效的人工检测方式一旦导致存在故障隐患的交叉杆的错误检测，则会影响到铁路货车的运行安全，造成巨大的经济损失。因此，实现对交叉杆相关几何参数的自动化检测有着很大的学术价值和经济价值。本文主要研究货车交叉杆平面度的自动检测算法。

1　交叉杆平面度检测算法的设计与实现

本文采用OpenCV（Open Source Computer Vision Library）为软件开发平台，该软件能够在Windows、Linux等多种操作系统上运行，有一套C函数和C++类构成的函数库，开发人员可以免费调用该函数库中的函数，极大地减小编程工作量，实现了图像处理和计算机视觉方面的很多通用算法。

1.1图像处理算法总体结构

在获取交叉杆圆形端头的图像后，需要利用图像处理的方法对所获取的图片做滤波，局部对比增强，去背景化，进而提取待测目标边缘，检测出目标圆心图像坐标，最终通过坐标变换计算出平面度参数，实现平面度检测算法，其算法流程如图1所示。

1.2局部自适应对比度增强

在铁路货车交叉杆检修线上，环境十分恶劣，存在着机械振动、光线亮度变化、电磁波干扰等使得相机采集到的图像有些模糊，对比度差，导致边缘提取的难度大大增加且提取效果差 。在对比度增强方面可分为全局增强和局部增强两种。全局增强方法简单却没有考虑局部图像信息，且直方图均衡化存在噪声过度增强的缺点。结合实际使用环境，均衡各种算法优缺点，本文采用基于局部标准差的自适应对比度增强算法，该算法关键在于确定对比度权值K。

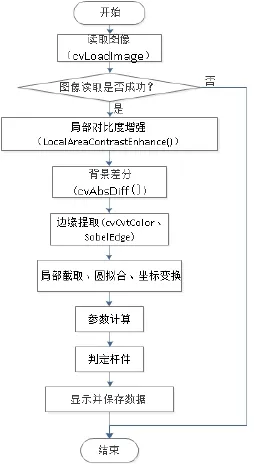
图1　图像处理算法流程图

x（i，j）设为图像中任意像素点的灰度值，其局部邻域为在以其为中心的（2n+1）×（2n+1）的区域，则图像的局部均值（即图像低频部分）和方差分别为：

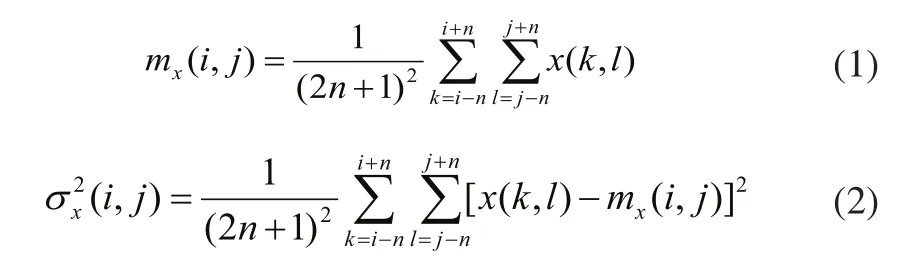
其中，σx（i，j）为局部标准差。设f（i，j）为对比度增强后的对应点的像素的值，则该算法的数学描述为：

其中，函数G（i，j）就是对比度权值K。由式（3）可看出，若G（i，j）＞1时，即可增强图像高频部分x（i，j）-mx（i，j）；若G（i，j）＜1，即可抑制图像高频部分，故算法中通常取K＞1，而当G（i，j）取常数k（k＞1）时，该部分同比例放大，此时高频部分可能出现过度增强现象。为解决这一问题，本文采用了自适应的对比度权值对图像高频部分进行差别化放大，算法的数学表达式为：

其中，D在本文算法为图像所有像素点像素值的均方差，为了约束高频部分过度增强，本文在算法的实际实现中加入了两个参数P和K，分别表示像素点的最大像素值和最大对比度放大增益值。如果f（i，j）＞Pmax则，f（i，j）＞Pmax；f（i，j）＜Pmax则f（i，j）的值为本身。参数K与P类似。

利用以上算法原理，通过实际编写函数LocalAreaContrastEnhance（）实现局部对比度增强的功能，如图2所示。

图2　局部对比度增强处理前后的交叉杆端头

1.3背景差分

摄像机在工业现场采集的图像除了包含有交叉杆的图像外，还夹杂有复杂的背景图像。在实际边缘提取中所获取的边缘其实是不同物体之间的边界，因此需要去除图像中的背景，剩下仅含有被检测目标的图像，则能够准确而快速的提取目标的边缘。

为了去除复杂背景，本文采用背景差分［1］的方法。其主要步骤为：

1）利用相机先获取支撑架升起前的图像，图3（a）作为检测目标背景；

2）再用实际获取的交叉杆圆形端头的图像，图3（b）和背景图像逐点做差分；

3）取合适的阈值T，若某点的灰度值差分大于阈值T，则取该点灰度值差分为该点新的灰度值，若灰度值差分小于阈值T，则取该点灰度值为0。

利用以上步骤就可实现目标与背景的分离，如图3（c）所示。从图中可以看出，检测目标突出，其他物体被削落。

图3　交叉杆端头进行背景差分前后的图

1.4目标边缘提取

边缘是指图片中像素真实值突然变化的区域，提取检测目标边缘的目的在于尽可能接近的获取其真实的边界。总结当前边缘检测算法方面的研究［2.3］，常用的算法可以分为基于一阶偏导数的边缘检测算法和二阶偏导数的检测算法。

在交叉杆检测系统中，每根交叉杆（由双杆构成）不超过4min，而在时间上Canny算法的运算时间最长，单幅图片的处理时间约为Sobel算法的10倍，因此本文给出了一种基于自适应阈值的改进Sobel算法来提取目标物体的边缘。改进的Sobel算法使用的模板分为X和Y两个方向且模板内的数值大小取决于中心点及其邻域内的点之间的距离，边缘点确定采用双阈值，分别为：TH1和TH2，其中，TH1的大小取决于整幅图像最大值（即最大值前乘上一定的权值，本文在实际边缘提取算法中取0.45），用于初步边缘提取；TH2的大小取决于8邻域内梯度的最大值（权值常取0.7～0.9），用于细致化的边缘提取。显然两个阈值都具有一定的自适应性。

利用以上原理编写自定义函数SobelEdge（），实际提取的边缘效果如图4所示。通过对比可知，原算法虽然提取到了更多的边缘，但是模糊不清晰，且多为离散的点，改进后算法提取到了圆形端头清晰的上半圆，而且图像连续，改进的模板适合于当前检测环境下的边缘提取。

图4　Sobel原算法（左）和改进算法（右）

1.5目标圆心检测

本文对于目标图像处理的最终目的是提取交叉杆圆形端头在图像坐标系中的圆形坐标。为了实现交叉杆圆心检测，本文采用两步获取圆心的位置坐标：

1）截取局部图像

本文中所使用的工业相机获取的图像大小为2592×1944（即500万像素点），为提升数字图像的处理速度，本文对所获得的边缘图像采用局部截取的方法来获取交叉杆圆形端头上半部分的边缘图像。

2）提取圆心坐标

通过局部图像截取处理后，获取的仅仅是交叉杆圆形端头的一部分，为了获取圆心的图像位置坐标，本文采用最小二乘法来拟合交叉杆的圆形端头，并最终间接提取圆心的图像位置坐标。

最小二乘法（least squares analysis）［4］是一种利用约束条件估算待定参数，使得该参数与其真值之间误差的平方和最小的参数估计算法。最小二乘法是曲线的拟合估计最为常用的方法［5］。

根据圆的数学描述，其标准方程可表示为：

其一般形式的方程可表示为：

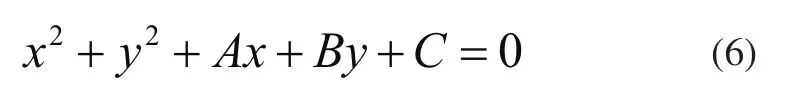
根据方程的一般式可知，则可以由A、B、C计算出圆心坐标以及半径大小，即：

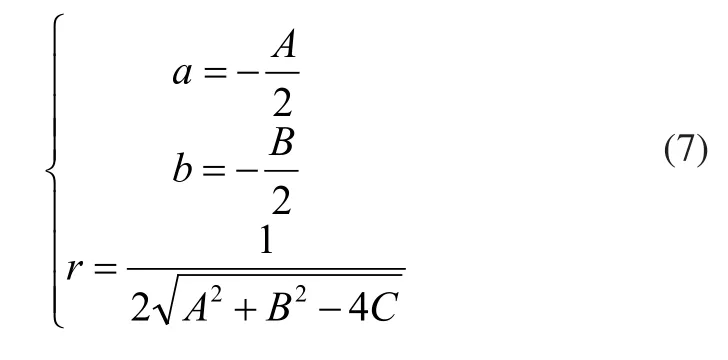
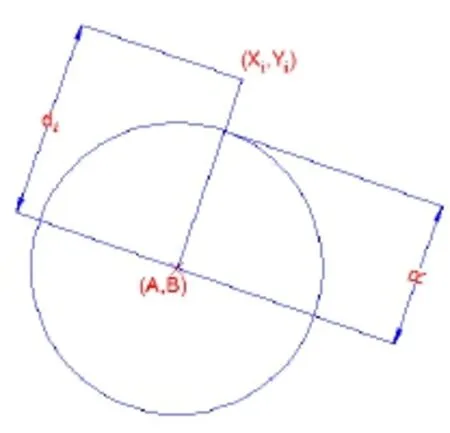
图5　圆拟合示意图

样本点（Xi，Yi）中点到圆心的距离为di：

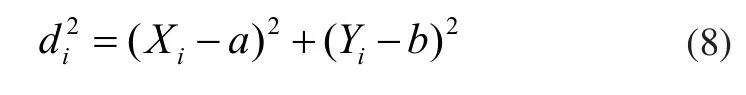
点（Xi，Yi）到圆边缘的距离的平方和与半径平方的差为：

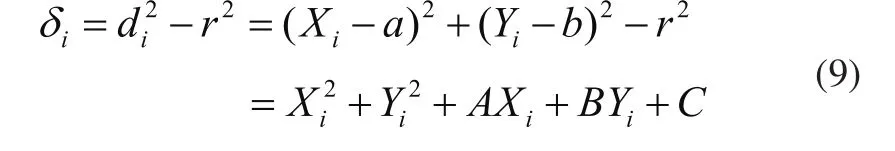
利用样本估算出参数A、B、C使得F（A，B，C）最小，并且求出圆心坐标和半径。

最终不仅获取了交叉杆圆形端头边缘图像（图6），且获得了图像中的圆心位置坐标。

图6　圆形端头拟合图

1.6坐标变换

本文中平面度的参数采用异面直线的距离来表示，故需要获得四个圆形端头ABCD的圆心的在物体坐标系中的坐标值。相机固定时借助十字标尺，光心位置尽可能正对标准杆的圆心位置，且光心与圆心距离固定在

250mm处，则Zc=（250+δ）mm，其中δ是交叉杆变形或者支撑架支撑时的位置偏差总和，3mm，大大小于250mm，对圆形端头在成像平面的投影坐标影响极小，故实际计算中取Zc=250mm。经过标定得到相机A的外参矩阵C0为：

将内外参数矩阵带入式（11）：

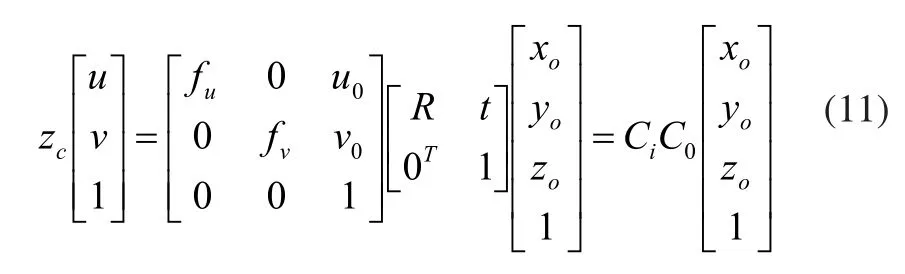
经过变形可得：

将圆拟合得到的A端头圆心像素坐标代入式（12），即可得到A的物体坐标系中的实际坐标值A（XA，YA，ZA），同理可得BCD点实际坐标值，分别为B（XB，YB，ZB）、C（XC，YC，ZC）、D（XD，YD，ZD）。

1.7平面度计算

根据空间几何相关数学基础可知，求异面直线的距离实际上就是求异面直线上任意两点的向量在其公垂线法相量上的投影。设1AC、1BD的公垂线法相量为n，则利用式（13）可求出平面度参数。

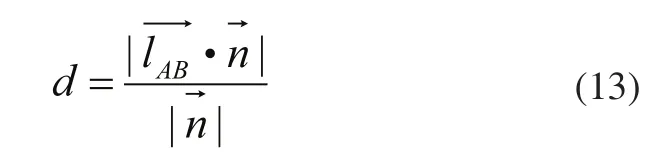
2　实验结果与分析

1）实验测量

根据实际项目要求测量指标如下：转8G（8B）型焊端头中心的平面度≤2mm，测量精度±0.1mm，重复性测量标准差＜0.065mm。分别对随机抽样的10根交叉杆（编号为1～10）进行自动测量和人工测量，测量的数据如表1所示，自动检测的1、2、4号交叉杆的平面度＞2mm，为废杆，不合格率为30%，而人工检测的1、2、4号同样也为废杆，不合格率为30%。自动测量与人工测量的数据基本吻合，且误差值均＜0.2mm。

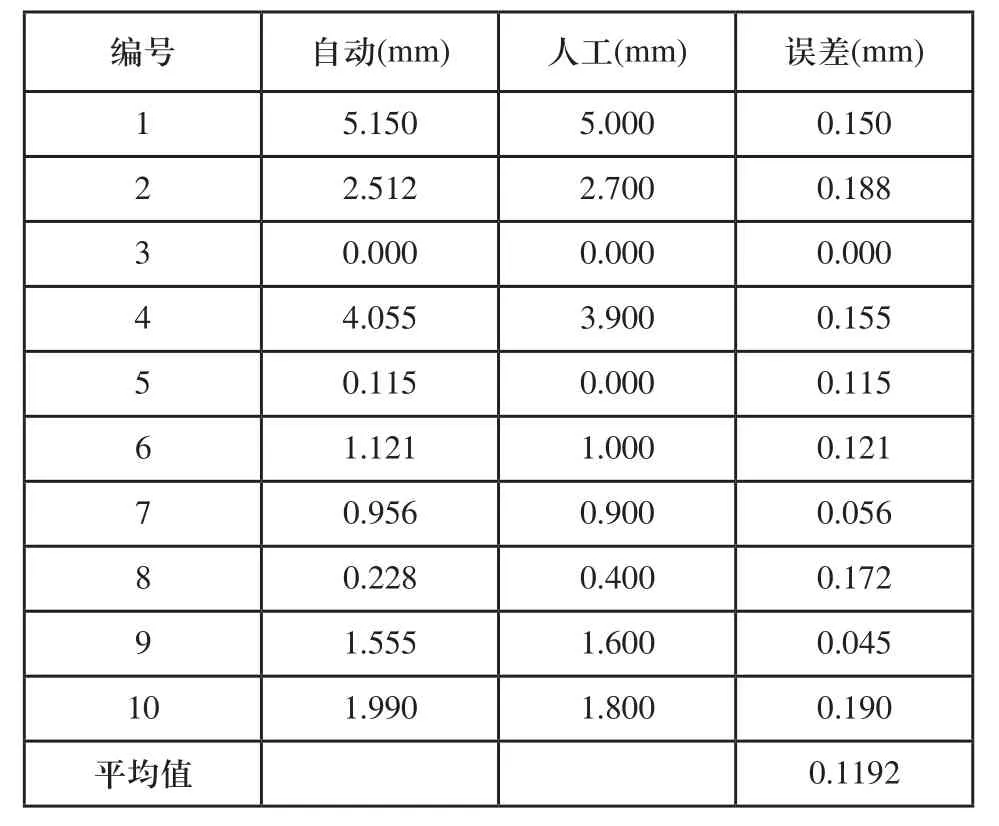
表1　随机抽样测量数据表

2）重复性测量

选取1、7、10号杆件，分别对三根交叉杆进行10次重复性自动测量，将测量的实验数据（表2）绘制成折线图。由图7可以看出，1号、7号、10号杆件在10次重复自动测量中平均值分别为5.033mm、1.048mm、1.989mm，单次测量与平均值之间的误差绝对值＜0.100mm，标准差分别为0.058mm、0.056mm、0.054mm。可见，自动测量的数据总体上的重复性较好。

表2　重复测量10次数据表

图7　1号、7号、10号交叉杆平面度重复测量结对比图

3　结论

本文以数字图像处理的相关原理及算法为基础，通过非接触式测量采集到货车交叉杆的图像。针对流水线现场光照不均且存在亮度变化的情况，给出了一种结合背景差分的局部自适应对比度增强算法，有效抑制背景对检测目标的影响并且能够较好的消除因光照变化对边缘提取的影响。利用改进了的Sobel算法提取检测目标的边缘。采用局部截取圆弧边缘图像，再结合基于最小二乘法的圆拟合方法来间接确定圆心的像素坐标，计算出交叉杆的平面度。结合实际情况以及对检测结果分析，采用自动测量交叉杆的平面度，提高了检测的精确度，满足对测量系统的误差要求。实现了测量的自动化，具有一定的应用和推广价值。

［1］ 屈晶晶，辛云宏.连续帧间差分与背景差分相融合的运动目标检测方法［J］.光子学报，2014，43（7）:（0710002-1）-（0710002-8）.

［2］ 余金栋，张宪民.用于线纹显微图像的边缘检测算法［J］.光学精密工程，2015，23（1）:271-281.

［3］ 师文，朱学芳，朱光.基于形态学的MRI图像自适应边缘检测算法［J］.仪器仪表学报，2013，34（2）:408-414.

［4］ 邹乐强.最小二乘法原理及其简单应用.科技信息［J］.2010（23）:282-283.

［5］ 李英硕，杨帆，袁兆奎.空间圆形拟合检测新方法［J］.测绘科学，2013，38（6）:147-148.

Research on the flatness detection algorithm of train’s cross rod based on image processing

WANG Yan-yan1，LU Wu-yi2，ZHENG Cong-min2

TP29

A

1009-0134（2016）09-0057-05

2016-06-06

王燕燕（1984 -），女，山西临汾人，讲师，工程硕士，研究方向为智能控制及其应用。