加一加 遮一遮 换一换
周虹

实际教学中,有些老师往往乐意追求在低等级水平技能(如简单的计算技能)上“高频”练习,却使得学生在高等级水平技能(如数感意识、数学思想)上“低频”发展,这样的弊端引发了我的思考。运算能力的高低,直接影响数学学习的能力。因此在教学实践中,我尝试着从改造教材习题入手,希望能在培养学生数感意识、数学思想等方面起到四两拨千斤的效果。
一、加一加
在教材习题的基础上加点料,帮助学生将零散的、单一的知识串联起来形成片。这样的习题改造,让学生“见山不只是山”,真正达到触类旁通的目的。
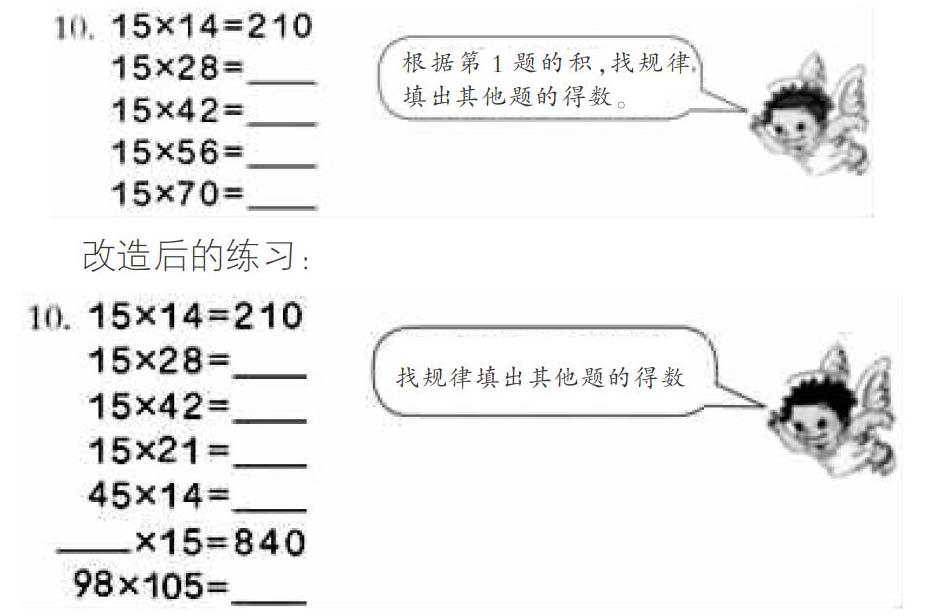
【案例1】《三位数乘两位数》教材练习:
改造后的练习:
改造后的习题,一方面对题目要求进行“扩容”:不局限于根据第1题15×14的积填写,不规定方法,如第3小题“15×42”可以与第1小题“15×14”进行比较解决,也可以利用乘法结合律将第1小题“15×14”和第2小题“15×28”的得数相加来解决,不同的学生会有不同的解题策略,培养了学生思维的灵活性。
另一方面,对知识点、解题方法进行“扩充”:如第6小题“ ×15=840”则是对积变化规律的逆向练习;而补充第7小题“98×105= ”,也是对积的变化规律的拓展延伸。
二、遮一遮
学生在平时作业中,见得最多的是“成品”式练习题:只要根据运算规则,计算得数即可。这样的计算题,目的是检测学生的计算技能。在长期的“成品”式练习下,师生们对于解决问题过程中的策略、数学思想方法等关注甚少。因此,在习题设计中可以将关键部分遮一遮,把“成品”变成“半成品”提供给学生,发展其思维能力。
【案例2】教材原题:列竖式计算:246×78。
改造后的练习为:
选择题:算式2□6×□8中有2个数字看不清楚,你觉得这个算式的得数可能是( )
A.30018 B.23566 C.19188 D.3568
改造后的练习,因两个乘数都是未知数,因此关闭了学生擅长的计算通道,迫使学生通过观察对比、算个位、乘数位数与积位数的关系、极限思想来解决:
通过两个乘数的个位6和8,确定积的个位一定是8,可以排除B;
利用极限思想,方框里分别填最小的数0和1,2□6×□8≈200×18=3600,可以排除D;
方框里填最大的数9,2□6×□8≈300×100=30000,可以排除A。
所以正确答案是C。
因此,在习题设计时可以像这样“露一半遮一半”,适当“留白”,让学生探究的兴趣更浓,获得的体验更深,也使得学生的数学学习更有思辨的味道。
三、换一换
怎样的题意要求更能启发学生的思维?我们可以用“换一换”的方法,换掉原来明确的要求,这样一换给学生思维发展提供更多空间。
【案例3】教材原题:
以“328×25”为例,把题目要求改为“用合适的方法计算”,学生呈现的方法罗列为:
(1)采用列竖式的方法;
(2)根据积不变性质将其转化为(328÷4)×(25×4)来解决;
(3)利用数的分解,再利用乘法结合律计算82×4×25=82×(4×25)。
因为在题目设计时换了要求,学生解决方法从单一的列竖式变得多样了,他们会根据数的特征选择合理的算法。如看见25想到4,再看看328里面有没有4这个因数。让学生选择“合适的方法”,培养了他们综合运用所学知识来灵活解决问题的能力。
(作者单位:浙江省杭州经济技术开发区学正小学)

