题组教学 魅力何在
杨迎冬


练习是学生巩固新知获得能力的必要手段。教学实践也表明,并不是练习做得越多就越好。在平时的教学中,很多有经验的老师会将几道有内在联系的题目,按照一定的逻辑顺序,汇编成有针对性、层次性、发展性的题组让学生集中练习。这样精心组合的题组,能充分发挥其整体功能,优于无组织的分散练习。这样的题组能纠正错误、查漏补缺,还能帮助学生提升思维品质、形成知识结构。
一、设计“对比型”题组,在辨析中凸显本质特征
有比较才有鉴别,人们对新事物的认识,几乎都是在旧事物的参照下实现的。
【案例1】教学“小数的大小比较”
在教学“小数的大小比较”时,老师在几张卡片上大做文章,用足用活了卡片,为课堂增色不少。
上课伊始,在黑板上贴出长方形的空白卡片□□□□和□□□□□,指着卡片,提问:如果这些卡片分别代表两个数,你觉得哪个数大一些?为什么?
随即在两个整数的方框中间都点上小数点,变成□□.□□ 和 □□.□□□,提问:现在你觉得哪个小数大一些?让学生猜测大小。
(预设学生的回答有两种情况:后面的大或不能确定。)
老师追问:为什么?
从知识层面来看,“小数大小的比较”是在“整数大小的比较”基础上进行的。而二者之间既有联系又有区别。受此影响,学生学习本节课的知识很容易误以为“位数多的那个小数就大”,如何解决这个问题?老师的做法是直面矛盾,抓住新旧知之间的联结点,将整数的大小比较和小数的大小比较进行有机的对接,以几张空白卡片作为切入点,在比较中体验二者的不同。
第一步实际上是在进行整数大小的比较,空白卡片显得更有研究价值:因为“空白”,所以更加聚焦:不再是就具体某两个数来比较,而是着重一般规律的提炼,把学生的注意力聚焦到了整数的位数上,五位数一定比四位数大,位数多的那个数就大。第二步,加上了小数点后形成的两个小数,情况就复杂了。学生甚至可以举出一些反例来证明:如95.23大于13.678,让学生初步感知到小数大小的比较与整数大小比较之间的不同之处:整数比较时,位数多的一定大;但是小数比较时,位数多的小数就不一定大。
二、设计“派生型”题组,在变化中培养灵活思维
学生在数学学习的过程中,由于受年龄、经验的局限或者惯性思维的影响,对概念的认知往往表现出孤立、肤浅的特征。这种思维的狭窄性具体表现在:根本想不到;只知其一,不知其二;或者是不会变通,条件稍有变化,就不知所措;或者知其然但不知其所以然。我在教学实践中发现,选择题中错误几个选项,恰恰是学生易犯的错误,往往极具迷惑性,貌似“错得极有道理”,很有辨析价值,值得深挖下去。
比如由一道选择题可以派生出来的几道题,组成题组,实战效果不错。
【案例2】考试中有这样一道选择题:
把2米长的绳子平均分成4份,每份长( )米?
A.4÷2 B.2÷4 C.200÷4
很多学生误选A,错因是学生对除法的意义并没有深刻领会,再加上平时里见到的除法算式一般都是被除数比除数大,受此负面影响。如果只是把正确答案B选出来,这道题的训练价值就大打折扣了。我的做法是逆向改正:即分析错误选项,假设错误的答案为正确,改前面的条件:在什么情况下,正确答案就应该是A和C?学生们经过思考,回答:
练习不在于多,而在于“精”,小题目里其实隐藏着大智慧。一题多用,一材多练,这样做一题,相当于做三题,学生们对除法意义的理解更加深刻了。
三、设计“阶梯型”题组,在拾级中揭示本质规律
前一个问题的解决, 为后一个问题的解决做铺垫, 最后水到渠成。一位老师教学“商中间有0的除法”,通过对例题的学习,学生大都能很快理解商中间有0的道理,并能掌握相应的计算方法。看似学会了,没有疑问了,但是,“无疑者,须教疑,有疑者,却要无疑,到这里方是长进”,小学生一般是不会去追根溯源地深入研究“为什么”。为此,老师设计了一组练习,让学生像爬楼梯一样拾级而上,自奋其力,感悟蕴含的本质规律。
【案例3】教学“商中间有0的除法”
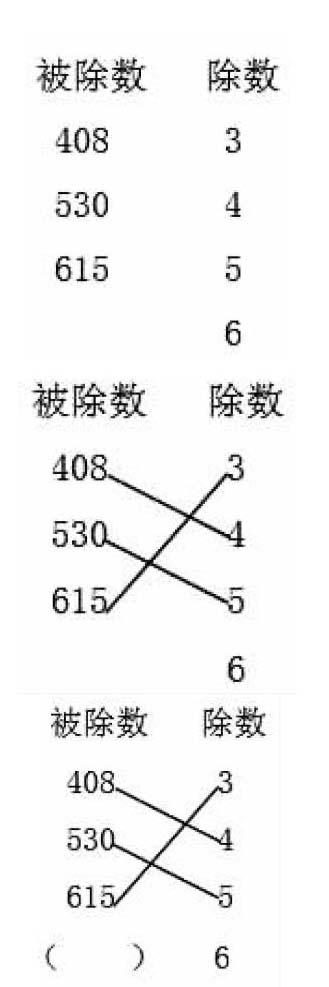
1.连线练习——基本训练
左边有3个数,表示被除数;右边有4个数,表示除数(如下图)。
要求学生观察并连线使被除数除以除数,商中间要有0。
2.填空练习——开放训练
学生经过观察、思考,相继连出三条线。
然后老师引导:这么多被除数和除数都交了好朋友,只有除数6还没有好朋友,谁能在括号里填写一个合适的被除数,使它除以6,商中间有0。
学生相继在括号里填写了: 606、6006、612、624、1224、630、3630……这些被除数,有的中间带0,有的中间不带0,有三位数也有四位数,例子越来越多,它们的共性也越来越明显。于是老师又趁机提出了新的要求:谁能试着说出在什么情况下不够商1需要写0占位?
3.总结提炼——感悟升华
对三年级的学生来说,这是挺难回答的问题。但是有前面的“阶梯”式练习铺垫,他们已经熟知其中的沟沟坎坎。经过一番激烈的讨论之后,终于有一个虽不严密但非常可贵的结论“出炉”,即:除到某一位时恰好没有余数,而下一位又比除数小,就出现了不够商1,需要写0占位的情况。
把一个看似艰难的任务拆分成多个循序渐进的小任务,通过解答前面的铺垫小题,水到渠成地生成属于自己的结论,“跳一跳够得着”地领悟算理以及规律。这样,练习就有了层次和梯度,学生能收获到步步登高的愉悦感和成就感。
四、 设计“体系型”题组,在系统中构建知识网络
【案例4】苏教版三年级(下册)教材总复习中的第1题:先算一算,再比一比。
从计算过程和结果的外延上来说,这四道题几乎囊括了三位数除以一位数的可能出现的所有情况。
首先,让学生们回忆一下:刚才你们是怎样计算三位数除以一位数的?回顾计算方法:从最高位除起,如果最高位不够除,就看前面两位,除到哪一位商就写在哪一位上面,每次除得的余数都要比除数小。如果仅仅只是这样,还完全没有发挥该题组的潜在价值。
我们还可以要求学生把它们分分类:
1.有没有余数来分:第②③题有余数,第①④题没有余数。
那,没有余数的除法怎么验算?有余数的除法呢?最大的不同是什么?现在请你从中各选一题验算一下。学生验算后,师生共同总结验算方法。
2.按商的位数来分:第③题的商是两位数,其他算式的商都是三位数。
总结:三位数除以一位数,商可能是两位数,也可能是三位数。
追问:为什么第③题的商是两位数?
因为283百位上的2不够4除,商的最高位在十位上,所以商只能是两位数。其余算式的百位上的数都大于4,至少够商1,所以商都是三位数。
3.按商是否有0来分:第①②题为一类,第③④题为一类。
追问:为什么第③④题商里都有0?因为283除以4除到十位后没有余数,而且个位上3除以4不够商1,所以要添0占位。
第④题,因为百位上4除以4等于1,正好除尽,没有余数;十位上0除以4得0,所以十位上写0。
总结:可见,虽然商里都有0,但是出现0的原因是不同的。
并且商里0所在的位置也是不同的,一个在商的末尾,一个在商的中间。
……
小学生的一般特点是喜欢埋头做题,去解决一个个具体的实际问题,因为这是他们熟悉的“埋头拉车”。但是作为老师,我们有责任有义务引领他们一练一得,从一道题看到一类题,总结出一般规律,提炼出解题策略和数学思想方法,也就是他们陌生的“抬头看路”。■
(作者单位: 浙江省杭州经济技术开发区教育发展研究室)

