基于改进型Duffing振子的微弱信号检测研究†

王晓东　杨绍普　赵志宏

(1.石家庄铁道大学 机械工程学院, 石家庄　050043) (2.河北省交通安全与控制重点实验室, 石家庄　050043)



基于改进型Duffing振子的微弱信号检测研究†

王晓东1,2†杨绍普1,2赵志宏2

(1.石家庄铁道大学 机械工程学院, 石家庄050043) (2.河北省交通安全与控制重点实验室, 石家庄050043)

传统的微弱信号检测在检测信噪比很低的信号时效果不理想,针对在强噪声背景下微弱信号的检测问题,提出了一种由单Duffing振子建立混沌系统的非线性恢复力项用-x5+x7来代替的改进方法,与传统Duffing振子检测系统相比具有更强的鲁棒性.阐述了基于相平面变化进行微弱信号检测的工作原理.对时间尺度进行变换,实现了对任意未知微弱周期信号的检测,通过对噪声背景中的微弱周期信号检测进行仿真实验,最后通过真实的故障轴承信号检测验证,都获得较好的效果,为工程实际应用提供了一种可鉴的方法.

混沌,Duffing振子,微弱信号检测,仿真

引言

在现代信息处理技术领域,微弱信号的检测是一项重要内容,同时也是工程技术中人们获取各种有用信息的一种重要手段[1].微弱信号检测是利用电子学、信息论和物理学的方法,研究被测信号的特征和相关性,检测出被噪声掩盖的微弱信号.在背景噪声较强的情况下,传统的线性滤波检测方法一般会失效.因此,寻求一种新的检测方法成为迫切的任务.根据混沌理论[2-3]可知,混沌系统在一定条件下对微弱信号具有敏感性的同时对噪声具有一定的免疫力[4-5],使得它在微弱信号检测中非常具有潜力,可以利用混沌系统这一特性来检测微弱信号.近年来,利用混沌系统检测微弱信号受到众多学者极大的关注[5].随着微弱信号检测方法在物理、化学、生物医学、机械、地质勘探、水声探测、雷达等各领域中的广泛应用[6],从而推动了整个科学技术的快速发展.

在复杂环境噪声干扰情况下,低信噪比信号的处理是当前信号处理研究的热点[7].微弱信号由于其幅值很小,测量时又受传感器和测量仪器的限制,表现出的总体效果都是有用的被测信号被多种强信号所湮没,从而很难测出,故而需要一种办法,既能将强噪声背景下的微弱信号提取出来,同时也能将噪声信号抑制下去.本文提出一种基于Duffing振子[8-10]改进的方法建模来检测微弱信号的方法,通过对此改进型Duffing混沌系统进行相图、庞加莱截面图、Lyapunov指数,研究分析了它的非线性动力学行为,阐述了基于相平面变化[11-12]进行微弱信号检测的工作原理,与传统Duffing振子检测系统相比具有更强的鲁棒性.通过对噪声背景中的微弱周期信号检测进行仿真实验和真实的故障轴承信号检测,获得较好的效果,为工程实际应用提供了一种可鉴的方法.

1　Duffing振子系统的检测原理

Duffing混沌振子系统在外加的激励信号的作用下会出现一系列的动力学特性,其中由混沌状态跃迁为大周期状态表现最为明显,并且跃迁的阈值很精确.使用Duffing混沌振子基于相平面变化检测微弱信号的原理如下：首先设置激励信号的幅值略小于跃迁阈值fd,此时系统处于混沌状态;其次,将待检测微弱信号与噪声作为激励信号项加入到Duffing振子系统中,假如此叠加的信号中含有一个与激励信号同频率同相的信号,并且此信号幅值与激励信号的幅值相加能大于跃迁阈值fd,此时混沌系统的输出相图将会转变为大周期状态.因此观察混沌系统前后相图的变化,就可以判断是否有微弱周期信号存在.

1.1建立混沌检测系统

建立对正弦信号敏感的混沌系统是信号检测的首要条件,采用Homes型Duffing振子作为模型,具体形式如下：

(1)

这是一个描述非线性弹性系统的运动方程,其中c表示阻尼比;-x+x3表示非线性恢复力;fcos(ωt)表示周期策动力;ω表示角频率,θ表示相位(一般θ=0).当c取某一固定值时,通常取c=0.5,较小时,相轨迹表现为Poincare映射意义下的吸引子,相点围绕焦点做周期振荡,逐渐增加f达到临界值fd时,系统经历同宿轨道,倍周期分岔直至混沌运动(如图1(a)所示),当超过临界阈值fd时,表现为大周期运动(如图1(b)所示).

图1　Duffing振子系统相图Fig. 1　Phase diagram for the Duffing oscillator system

2　Duffing振子的改进

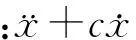
2.1系统的Lyapunov指数谱图

Lyapunov指数是目前描述混沌一个很重要的指标,通过求最大Lyapunov指数是否大于0来判断系统的状态,当最大Lyapunov大于0时,系统是混沌的,而当最大Lyapunov指数小于0时,系统则是周期的.图2为Lyapunov指数谱图,通过图2可以看出系统主要在周期状态和混沌状态之间交替出现,在周期策动力幅值f小于0.18时,最大Lyapunov指数小于0,系统运 动轨迹比较简单处于周期一状态,然后随着f的不断增大,最大Lyapunov指数开始出现大于0的情况,即运动轨迹出现杂乱无章的混沌状态,大概在f=0.43左右,系统又进入周期运动,继续增大f的值,系统又进入混沌状态,并在较大一段策动力幅值内保持混沌状态,当在f=0.75左右,系统又进入大周期运动,并一直保持下去.此时相轨迹将焦点和鞍点统统围住,表现为Poincare意义映射下的不动点.

图2　改进型Duffing系统的Lyapunov指数Fig. 2　Lyapunov exponent of the improved Duffing system

2.2建立Simulink仿真模型

对上述改进的Duffing振子,由数学模型可建立此系统的仿真模型(如图3所示),采用定步长四阶龙格—库塔法,取步长h=0.01s,阻尼系数c=0.5,进行仿真计算.该二阶微分方程存在固有的本征频率,由于周期策动力的作用,在合适的策动频率下使得此系统表现出丰富的动力学现象,包括吸引子、同宿轨道、周期倍化分岔状态、混沌状态和大周期状态.随着周期策动力f从0逐渐增大,当幅值超过某个阈值之后系统处于混沌状态,相轨迹局限在某一个范围内,系统相图如图4(a)所示;继续增大激励信号的幅值,当再次超过某个阈值之后,系统进入大周期状态,如图4(b)所示,相轨迹不再杂乱无章,而是沿着固定的轨道重复下去.

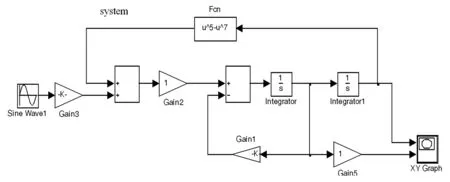
图3　Simulink仿真模型Fig. 3　Simulation Model of Simulink

图4　改进型Duffing系统的响应图Fig. 4　Response of the improved Duffing system

通过大量的实验,选择适当的参数,观察系统相图、时域图、庞加莱截面图、功率谱图变化的方法确定了此系统的阈值fd=0.75049,当策动力幅值等于fd时,系统处于混沌状态;当策动力幅值大于fd时,系统处于大周期状态.

2.3未知频率信号的检测模型

前面讨论了周期频率为ω=1.0rad/s的改进Duffing方程系统,而实际的工程应用中要检测的信号大多都是未知的,因而无法确定其确切的检测频率,为了减少计算的麻烦,可以对方程进行时间尺度的变换,以便能用于对任意未知信号的检测.

令t=ωτ,则：

X(t)=X(ωτ)

(2)

(3)

(4)

上述以时间尺度τ的变化过程,其状态方程可以写成以下形式;

(5)

这样只需调整方程(5)式中的ω值,来适应外界不同频率的周期信号,从而实现对外界不同频率的微弱信号的检测.由于状态方程(5)是由上述方程派生出来的,只是从另一时间尺度观察变形检测系统的动态,因此前面所讨论的结果,系统的性质,以及相态变化的阈值等,都是适用的.对于上述变形非线性系统的模型,设置其它参数不变,进行不同频率的周期信号检测,改进型检测系统相图(5)是取ω=2.0rad/s时进行的实验验证(混沌状态、周期状态).通过仿真实验分析,该变形是正确的、可靠的.在Duffing方程改进后,可根据实际情况调整参数以进行系统各个状态的仿真和计算.

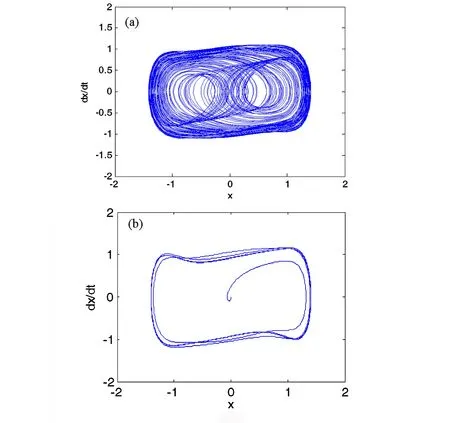
图5　改进型Duffing振子的相图Fig. 5　Phase Diagrams for the system of improved Duffing

3　微弱信号检测模型

将待测信号S=acos(ωt+φ)+n(t)(a为待测信号幅值.n(t)为噪声)作为周期策动力的摄动并入系统.调整Duffing方程使f=fd,当待测信号加入系统中经过暂态过程以后,系统稳定在某一运动形式上,计算机通过辨识系统容易得知系统是处于混沌还是大尺度周期运动状态.由此,可判断输入的信号是纯噪声还是混有微弱周期信号.

A(t)=fcos(ωτ+θ)+acos(ωτ+φ)=

f[cos(ωτ)cos(θ)-sin(ωτ)sin(φ)]+

a[cos(ωτ)cos(φ)-sin(ωτ)sin(φ)]

当相位θ=0时：

A(t)=[f+acos(φ)]cos(ωτ)-

asin(φ)sin(ωτ)=

γ(τ)cos(ωτ+φ(τ))

其中：

从上式可以看出系统相态和相位之间的关系.调整策动力可以使待测信号的相位满足下式：

π-arctan[(a/2f)]≤φ≤π+arccos[(a/2f)]

使系统处于混沌状态,不会产生到大周期的变化.

当系统没有同频率待测的周期的信号输入时,系统输出的呈现如图6(a)的混沌现象.当系统有相同频率的待测周期信号acos(ωt),其中a=0.00005,输入系统时,系统输出的呈现如图6(b)的大周期现象.

图6　改进型Duffing振子的相图Fig. 6　Phase Diagrams of the improved Duffing system

由上述非线性系统的相态变化的仿真结果显示,可求得此时的信噪比检测的最低门限为:

4　与Duffing振子性能比较

在两种检测模型中,包含内置周期策动力和作为外加周期策动力并入系统的待测信号.由于仿真的目的是比较两种系统的稳定性和抗噪性能,而不是检测微弱信号,所以未将微弱信号单独写出.对于微弱信号检测,系统经临界态将进入大尺度周期状态,此状态的稳定性对于系统的判断很重要,这里分别利用两种系统在不同强度噪声背景中的稳定性进行分析.

两种不同强度的噪声分别为噪声幅值为0.3和噪声幅值为0.5,两个系统在不同强度噪声背景中的周期运动相态如图7,在不同强度噪声背景中,改进的Duffing系统保持着良好的周期运行状态,而Duffing系统存在不稳定性,由于存在噪声,使两系统的运行轨迹都较粗糙.

图7　两种Duffing振子系统鲁棒性比较(a、c为Duffing系统;b、d为改进Duffing系统;且a、b噪声幅值为0.3;c、d噪声幅值为0.5)Fig. 7　Comparison of the robustness between two Duffing oscillator systems (where, a and c for the Duffing system, b and d for the improved Dufing system, a and b for the Noise amplitude of 0.3, c and d for the Noise amplitude of 0.5)

5　滚动轴承早期故障诊断应用

作为机械设备关键部件之一,轴承的早期故障诊断显得尤为重要.对于轴承的早期故障,由损伤引起的冲击信号大多被淹没在强噪声中,用传统的信号分析方法很难识别这种故障信息.

通过模拟信号对改进型Duffing振子进行仿真,证明可以检测出故障信号,为了验证改进型Duffing振子系统在现场能够应用,本文采用河北省交通安全与控制重点实验室的振动测试试验台,测量时采用四通道加速度传感器,采样频率为25600Hz,采样时间为10s,电机转速为1700r/min.下面采集的数据是某一轴承外圈数据(如图(8)所示),通过计算分析此轴承的故障频率在105Hz左右,将设计的改进型Duffing振子系统状态方程(5)内驱动力的频率设置在105Hz,然后将测得轴承信号代替原来的模拟信号输入到此系统中观察系统相图的变化,得到输入轴承故障数据前后改进型Duffing系统的相轨迹(如图9所示)

图8　轴承故障数据Fig. 8　Fault bearing data

图9　改进型Duffing振子的相图Fig. 9　Phase Diagrams of the improved Duffing system

6　结论

本文研究基于Duffing振子微弱信号检测中,通过对Duffing系统模型的改进,分析了在强背景噪声下对微弱周期信号检测的基本原理,给出了不同条件下的仿真实验结果,通过对比实验,此改进型系统具有更强的鲁棒性.并且通过真实的实验数据实验验证,该方法在旋转机械的状态监测和故障诊断中取得了很好的效果.对于其它非周期信号、色噪声检测等混沌振子检测方法的研究与探讨还在不断的进行中.

1夏均忠,刘远宏,冷永刚,葛纪桃. 微弱信号检测方法的现状分析. 噪声与振动控制,2011,5(3):156～161 (Xia Z J, Liu Y H, Lin Y G,Ge J T. Analysis of methods of weak signal detection.NoiseandVibrationControl, 2011,5(3):156～161 (in Chinese))

2Li Y, Yang B J. Chaotic Oscillator Systems(L-Y) and Detection. Beijing: Science Press, 2007:46～47

3聂春燕. 混沌系统与弱信号检测. 北京: 清华大学出版社,2009 (Nie C Y. Chaotic system and weak signal detection. Beijing: Tsinghua University Press, 2009 (in Chinese))

4Zhang X Y, Guo H X, Wang B H, et al. A new method for detecting line spectrum of ship-radiated noise using Duffing osci-llator.ChineseScienceBulletin, 2007,52(14):1906～1912

5李月,杨宝俊,石要武.色噪声背景下微弱正弦信号的混沌检测. 物理学报, 2003,52(3):526～530 (Li Y, Yang B J, Shi Y W. Chaos-based weak sinusoidal signal detection approach under colored noise background.Physic, 2003,52(3):526～530 (in Chinese))

6Hu W J, Liu Z Z. Study of metal detection based on chaotic theory. jinan: In:8th World Congress on Intelligent Control and Automation, 2010:2309～2314

7Zhang X Y, Guo H X,Wang B H, et al. A new method for detecting line spectrum of ship-radiated noise using Duffing oscillator.ChineseScienceBulletin, 2007,52(14):1906～1912

8吴参,李兴林,孙守迁等. 混沌理论在滚动轴承故障诊断中的应用. 轴承, 2013,12(1):60～64 (Wu C, Li X L, Sun S Q, et al. Application of chaos theory in fault diagnosiss of rolling bearings.Bearing, 2013,12(1):60～64 (in Chinese))

9李月,石要武,马海涛,杨宝俊.湮没在色噪声背景下微弱方波信号的混沌检测方法.电子学报, 2004,1(12):87～90 (Li Y, Shi Y W, Ma H T,Yang B J. Chaotic detection method for weak square wave signal submerged in colored noise.ActaElectronicaSinica, 2004,1(12):87～90 (in Chinese))

10王冠宇,陶国良,陈行等. 混沌振子在强噪声背景信号检测中的应用. 仪器仪表学报, 1997,18(2):209～214 (Wang G Y, Tao G L, Cheng H, et al. Application of signal detection chao Oscillator under strong noise.ChineseJournalofScientificInstrument, 1997,18(2):209～214 (in Chinese))

11齐雁,武晓春.基于Duffing振子的轨道移频信号检测方法研究. 铁道标准设计, 2015,59(3):106～109 (Qi Y,Wu X C. Duffing oscillator based track frequency-shift signal detection.RailwayStandardDesign, 2015,59(3):106～109 (in Chinese))

12任学平,刘桐桐.用改进型的Duffing理论判断轴承故障的微弱信号. 噪声与振动控制, 2014,34(1):173～177 (Ren X P, Liu T T. Detection of weak fault signals of bearings based on the improved duffing theory.NoiseandVibrationControl, 2014,34(1):173～177 (in Chinese))

*The project supported by the National Natural Science Foundation of China(11172182、11227201、11472179).

† Corresponding author E-mail: wx_dong@126.com

12 May 2015,revised 29 June 2015.

RESEARCH OF WEAK SIGNAL DETECTION BASED ON THE IMPROVED DUFFING OSCILLATOR†

Wang Xiaodong1,2†Yang Shaopu1,2Zhao Zhihong2

(1.SchoolofMechanicalEngineering,ShijiazhuangTiedaoUniversity,Shijiazhuang050043,China) (2.KeyLaboratoryofTrafficSafetyandControlinHebei,Shijiazhuang050043,China)

The effect of the traditional weak signal detection on low SNR is undesirable. this paper proposes an improved method for the detection of the weak signal under strong noise background. It replaces the nonlinear restoring force of a chaotic system by a equation of -x5+x7by means of a single Duffing oscillator. Compared with the traditional Duffing oscillator detection system, this method performs stronger robustness. It states the working principle of weak signal detection based on the phase plane changes, and any unknown weak periodic signal detection can be achieved through the conversion of the time scale. The simulation study on the weak periodic signal detection under the noise background is also carried out, and verified against the detecting results of the real bearing fault signal. It is found that the proposed method obtains good effect. It provides a reasonable method for the engineering application.

duffing oscillator,signal to noise ratio(SNR),weak signal detection,simulation

E-mail: wx_dong@126.com

10.6052/1672-6553-2015-055

2015-05-12收到第1稿,2015-06-29收到修改稿.

*国家自然科学基金资助项目(11172182、11227201、11472179)