Bayes线性无偏估计关于误差协方差及先验分布的稳健性

邱红兵

(广东工业大学 应用数学学院, 广东 广州 510520)



Bayes线性无偏估计关于误差协方差及先验分布的稳健性

邱红兵

(广东工业大学 应用数学学院, 广东 广州 510520)

对于线性模型中未知参数估计的稳健性的研究，一直是统计学中的一个热点.本文研究线性模型中回归系数的Bayes线性无偏估计关于误差协方差及先验分布的稳健性问题，分别得到当误差协方差改变、先验分布改变或误差协方差和先验分布同时改变时，Bayes线性无偏估计还保持其最优性的充分必要条件．

线性模型;Bayes线性无偏估计;稳健性;先验分布

1　问题的提出

考虑线性模型

y=Xβ+e，E(e)=0,Cov(e)=σ2T，

(1)

其中y为n×1的观测向量, X为n×p的设计矩阵，且rankX=k≤p,β为p×1的未知参数向量，e为n×1的随机误差向量,T为已知的n阶正定矩阵,σ2>0已知．

模型(1)常记为

MT=(y,Xβ,T)．

而T=I(I表示适当阶数的单位矩阵)时的模型记为

MI=(y,Xβ,I)．

设β有先验分布π(μ,V):

E(β)=μ,Cov(β)=τ2V，

其中τ2>0已知，V为p阶非负定矩阵．而当μ=η,V=I时β的先验分布为π(η,I):

E(β)=η,Cov(β)=τ2I．

取损失函数为二次损失函数

L(d,τ)=(d-τ)′(d-τ)．

当X为列满秩时，未知参数β在先验分布π(μ,V)下的Bayes线性无偏估计为

类似地，在线性模型MI下，可估函数Xβ在先验分布π(μ,V)下的Bayes线性无偏估计为

在线性模型MT下，可估函数Xβ在先验分布π(η,I)下的Bayes线性无偏估计为

在线性模型MI下，可估函数Xβ在先验分布π(η,I)下的Bayes线性无偏估计为

在线性模型的参数估计问题中，总是先给定误差协方差及先验分布，但在实际问题中，随机误差分布中的协方差矩阵可能略有偏差，同样先验均值与先验协方差矩阵也可能略有偏差，因此我们希望据此所做出的统计推断关于误差分布或先验分布具有稳健性．对估计的稳健性问题，已有不少文献，如文献[4-7]分别研究了未知参数β的最小二乘估计和广义最小二乘估计以及可估函数Xβ的Gauss-Markov估计关于误差分布的稳健性.对可估函数的Bayes估计的稳健性问题，也有不少文献，如文献[8-13]，其中文献[8]研究了模型错误指定下的Bayes估计的稳健性问题；文献[9]在错误先验假定下研究了回归系数β的Bayes估计的小样本性质，得到了错误先验假定下求出的Bayes估计，在MSEM准则及PPC准则下优于最小二乘估计的条件；文献[10]则研究了奇异线性模型中，在错误先验假设下获得的可估函数Xβ的Bayes线性无偏估计在MSEM准则和PPC准则下相对最小二乘估计的优良性问题.当设计矩阵X列满秩时，文献[11]和[12]分别在二次损失和矩阵损失下研究了β的Bayes线性无偏估计关于误差分布的稳健性，分别给出了误差分布的最大类，使得误差项的分布在此范围内变动时，β的Bayes线性无偏估计都是最优估计．文献[13]则研究了分块线性模型中Bayes线性无偏估计的可加性问题，得到了全模型下的Bayes线性无偏估计与小模型下的Bayes线性无偏估计相等的充分必要条件.

因此，本文主要解决上面提出的几个问题，研究可估函数Xβ的Bayes线性无偏估计关于误差协方差和先验分布的稳健性问题．第2节讨论可估函数Xβ的Bayes线性无偏估计关于误差协方差的稳健性；第3节考虑可估函数Xβ的Bayes线性无偏估计关于先验分布的稳健性；第4节研究可估函数Xβ的Bayes线性无偏估计关于误差协方差和先验分布的同时稳健性．

2　关于误差协方差的稳健性

XVX′(ρT+XVX′)-1(y-Xμ)+Xμ=XVX′(ρI+XVX′)-1(y-Xμ)+Xμ．

等价于

XVX′(ρT+XVX′)-1=XVX′(ρI+XVX′)-1．

上式两边同时右乘ρT+XVX′，并同时左乘ρI+XVX′，化简即得XVX′T=XVX′．

另一方面，若XVX′T=XVX′，则有

XVX′T(ρT+XVX′T)-1(y-Xμ)+Xμ=

XVX′[(ρT+XVX′T)T-1]-1(y-Xμ)+Xμ=

XVX′(ρI+XVX′)-1(y-Xμ)+Xμ=

定理得证.

例1设有混合模型

y=Xβ+Zγ+ε，E(ε)=0,Cov(ε)=σ2I，

(2)

这里Z为满足X′Z=0的n×q阶矩阵，β为p×1的固定效应向量，γ为q×1的随机效应向量，且满足E(ε)=0,Cov(ε)=σ2W.记e=Zγ+ε,则模型(2)可表示为

y=Xβ+e，E(e)=0,Cov(e)=σ2T，

其中T=I+ZWZ′．

3　关于先验分布的稳健性

XVX′(ρT+XVX′)-1(y-Xμ)+Xμ=XX′(ρT+XX′)-1(y-Xη)+Xη

对任意y∈Rn成立．取y=Xμ，得

Xμ=XX′(ρT+XX′)-1X(μ-η)+Xη=(ρT+XX′-ρT)(ρT+XX′)-1X(μ-η)+Xη=Xμ-ρT(ρT+XX′)-1X(μ-η)．

XVX′(ρT+XVX′)-1=XX′(ρT+XX′)-1．

上式两边同时右乘ρT+XVX′，并化简，得

T=T(ρT+XX′)-1(ρT+XVX′).

上式两边同时左乘(ρT+XX′)T-1，有XX′=XVX′．必要性得证．

充分性：若Xμ=Xη且XX′=XVX′，则

定理得证．

例2 在线性模型MT中，若未知参数β具有先验分布π(μ,V)：

μ=η+U′t，V=I+U′ΔU．

4　关于误差协方差及先验分布的同时稳健性

本节讨论可估函数Xβ的Bayes线性无偏估计关于误差协方差和先验分布的同时稳健性问题．有如下结果．

XVX′(ρT+XVX′)-1(y-Xμ)+Xμ=XX′(ρI+XX′)-1(y-Xη)+Xη

对任意y∈Rn成立．取y=Xμ, 得

Xμ=XX′(ρI+XX′)-1X(μ-η)+Xη=(ρI+XX′-ρI)(ρI+XX′)-1X(μ-η)+Xη=Xμ-ρI(ρI+XX′)-1X(μ-η)．

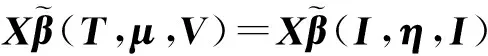
XVX′(ρT+XVX′)-1=XX′(ρI+XX′)-1.

上式两边同时右乘ρT+XVX′，并同时左乘ρI+XX′，化简即得XX′T=XVX′．

充分性：若Xμ=Xη且XX′T=XVX′，则有

定理得证．

[1] ZHANG W P, WEI L S. On Bayes linear unbiased estimation of estimable functions for the singular linear model[J]. Science in China Series A: Mathematics, 2005, 48(7): 898-903.

[2] 张伟平. 贝叶斯线性无偏估计[D]. 合肥: 中国科学技术大学统计与金融系, 2005.

[3] WEI L S, ZHANG W P. The Superiorities of Bayes linear minimum risk estimation in linear model[J]．Communications in statistics-theory and methods，2007, 36: 917-926.

[4] KARIYA T, KURATA H． A maximal extension of the Gauss-Markov theorem and its nonlinear version[J]．J Multivariate Anal，2002, 83: 37-55.

[5] 刘湘蓉. 最小二乘估计关于误差分布的稳健性[J]. 应用概率统计，2006, 22(4): 429-437．

LIU X R. On robustness of LSE in terms of error distributions[J]. Chinese Journal of Applied Probability and Statistics, 2006, 22(4): 429-437.

[6] 邱红兵, 罗季．线性模型中广义最小二乘估计关于误差分由的稳健性[J]. 吉林大学学报(理学版)，2009, 47(1): 13-16.

QIU H B, LUO J. On robustness of GLSE in terms of error distributions in linear model[J]. Journal of Jilin University (Science Edition), 2009, 47(1): 13-16.

[7] 邱红兵, 罗季．Gauss-Markov估计关于误差分由的稳健性[J]．应用概率统计，2010, 26(6): 615-622.

QIU H B, LUO J. Robustness of Gauss-Markov estimator in terms of error distributions[J]. Chinese Journal of Applied Probability and Statistics, 2010, 26(6): 615-622.

[8] Trenkler G, Wei L S. The Bayes estimator in a misspecified regression model[J]．Test，1996，5: 113-123.

[9] 韦来生. 错误先验假定下回归系数Bayes估计的小样本性质[J]．应用概率统计，2000, 6(1): 71-80．

WEI L S. The small-sample properties for the Bayes estimator of regression coefficients under misspecified prior assumption[J]. Chinese Journal of Applied Probability and Statistics, 2000, 6(1): 71-80．

[10] 张伟平, 韦来生. 错误先验假设下Bayes线性无偏估计的稳健性[J]. 应用概率统计，2007，23(1): 59-67.

ZHANG W P, WEI L S. The robustness of Bayes linear unbiased estimations under misspecified prior assumption[J]. Chinese Journal of Applied Probability and Statistics, 2007，23(1): 59-67.

[11] 邱红兵, 罗季，孙旭．Bayes线性无偏估计的稳健性[J]．湖北大学学报(自然科学版)，2012, 34(3)：324-326,339．

QIU H B, LUO J, SUN X. Robustness of Bayes linear unbiased estimation[J]. Journal of Hubei University (Natural Science), 2012, 34(3)：324-326,339．

[12] 邱红兵, 罗季．矩阵损失下贝叶斯线性无偏估计及其稳健性[J]．华东师范大学学报(自然科学版)，2013，1：24-29，53．

QIU H B, LUO J. Bayesian linear unbiased estimator and its robustness under the matrix loss function[J]. Journal of East China Normal University (Natural Science). 2013，1：24-29，53．

[13] 邱红兵, 罗季. 分块线性模型中Bayes线性无偏估计的可加性[J].广东工业大学学报，2013，29(1)：64-66.

QIU H B, LUO J.Additivity of the Bayes linear unbiased estimator in the partitionel linear mode[J]. Jourmal of Guangdong University of Technology, 2013, 29(4): 64-66.

Robustness of Bayes Linear Unbiased Estimator in Terms of Error Covariance and Prior Distributions

Qiu Hong-bing

(School of Applied Mathematics, Guangdong University of Technology, Guangzhou 510520，China)

The research that focuses on the robustness for the estimation of unknown parameters in the linear model has been a hot topic of statistics. In this paper, the robustness of Bayes linear unbiased estimator of the regression coefficients in the linear model in terms of error covariance and prior distributions are discussed, and the necessary and sufficient conditions for Bayes linear unbiased estimator holding its optimality when error covariance varies, or prior distributions vary, or error covariance and prior distributions vary, are respectively obtained.

linear model; Bayes linear unbiased estimator; robustness; prior distribution

2015- 12- 01

国家自然科学基金资助项目(11401114)；国家社会科学基金资助项目(11CTJ008)

邱红兵(1974-)，男，副教授，主要研究方向为线性模型．

10.3969/j.issn.1007- 7162.2016.05.002

O212.1

A

1007-7162(2016)05- 0005- 04