求解多目标背包问题的改进人工鱼群算法

黄美华， 温洁嫦， 何　勇

(广东工业大学 应用数学学院, 广东 广州 510520)



求解多目标背包问题的改进人工鱼群算法

黄美华， 温洁嫦， 何勇

(广东工业大学 应用数学学院, 广东 广州 510520)

作为一种新的群智能算法,在求解多目标背包问题时,人工鱼群算法存在盲目搜索、收敛速度慢和求解精度低等问题.针对这些问题,本文结合人工鱼位置全局最优信息,对人工鱼的移动策略进行自适应改进,提出一种改进的人工鱼群算法.对多目标背包优化问题实验仿真表明,本文改进的人工鱼群算法收敛速度和搜索到的非劣解的精度均优于粒子群算法和遗传算法.

多目标优化； 背包问题； 人工鱼群算法； 自适应

多目标背包问题是一个易于描述却难以解决的NP-hard问题,在现实世界中具有广泛的应用背景.投资组合、货物装载、工程设计等都可以建模为多目标背包问题.

随着背包内物品的数量增加,考虑物品的性质增多,多目标背包问题的求解空间和时间复杂度将呈指数级增加.大规模多目标背包问题的解空间很庞大,传统的计算方法面临着计算时间长、计算成本高和搜索高质量解难等问题,需要研究有效的搜索方法,使得在求解时间和求解精度上取得平衡.粒子群算法[1-2]、遗传算法[3- 4]和蝙蝠算法[5]等,代表一类模拟自然进化的随机优化方法，能在一次模拟运行中求出多个有效解[6],所以特别适合研究多目标背包问题.

作为一种新型仿生群智能优化算法,人工鱼群算法[7]具有鲁棒性强、全局收敛性好以及对初值要求低等优点.然而,由于人工鱼个体的行为都是局部寻优行为,所以难以避免个体趋同、早熟现象,从而陷入局部极值[8].因此,人工鱼群算法求解多目标背包问题存在收敛速度慢、求解精度不高、复杂度高等缺点.

针对上述缺点,文献[9-11]把全局最优人工鱼信息加入人工鱼的位置更新公式中，文献[12-15]根据鱼群整体状态的变化适时调整人工鱼的视野和步长对人工鱼群算法进行改进.

本文采用文献[12]中的自适应步长,加入全局信息[10],引入一个自适应因子,自适应调整全局信息在算法中的作用,以解决人工鱼群算法在求解多目标背包问题时收敛慢,求解精度不高的问题.通过计算机仿真,并与粒子群算法和遗传算法进行比较,采用文献[3]中的评价方法评价算法的收敛性和求解精度,证明本文改进的人工鱼群算法在多目标背包问题上的应用是有效的,且搜索到的解质量比较高.

1　多目标背包问题及其数学模型

假设存在m类物品,每类物品中又包含n种具体物品,现要求从这m种类别物品中分别选择一种物品放入背包中,使得背包内物品的总价值最大,总体积最小,并且背包的总质量不超过ckg.背包问题的数学模型为

其中,Px表示背包内物品价值,Rx表示背包内物品体积,C表示物品质量,X为选择物品.P为每个物品的价值,R为每个物品的体积,X为一个0-1矩阵,1表示该物品被选择,0表示该物品不被选择.P,R,C的取值如下：

2　人工鱼群算法

2.1人工鱼群算法基本原理

在一片水域里,鱼总是自行或尾随其他鱼朝该水域中营养物质最丰富的地方游动.人工鱼群算法就是根据鱼的这一自然特性,模仿鱼群觅食等行为,实现寻优.

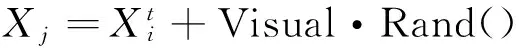
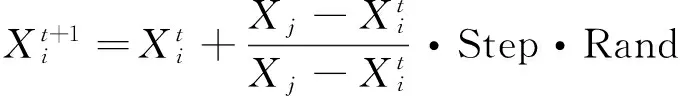
2.2人工鱼移动策略

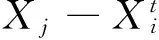
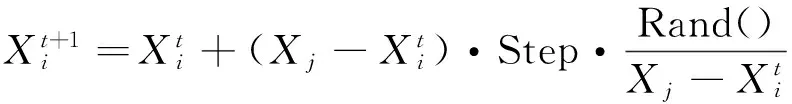
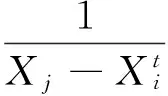
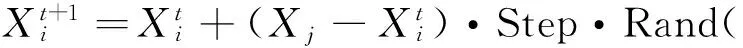
2.3自适应步长

在聚群行为和追尾行为中,步长是一个固定的参数,致使初期收敛速度较快,后期不易集中,最优解不精确.依据最优人工鱼与当前人工鱼的两种适应原则及食物浓度的比较,确定移动步长,表示如下：

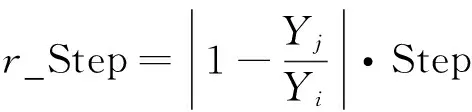
即算法中移动步长大小取决于当前所在状态和视野范围中视点感知的状态[12].

2.4全局人工鱼群算法

基本人工鱼群算法中,人工鱼的位置更新公式中只有局部信息没有全局信息.全局人工鱼群算法就是把人工鱼全局最优位置信息Xbest_af加入位置更新模式中,实现人工鱼全局寻优[9].位置更新表示如下：

3　改进的人工鱼群算法

本文引入一个自适应因子w，自适应调整全局信息在人工鱼寻找下一个位置时的判断和决策中的作用.其中，

w1>w2,Tmax为最大迭代次数,Tcur为当前迭代次数.

3.1改进算法人工鱼的行为描述

3.1.1觅食行为

若不符合则继续搜索,反复尝试Try_number次后，如果仍不符合前进条件,则随机移动一步

3.1.2聚群行为

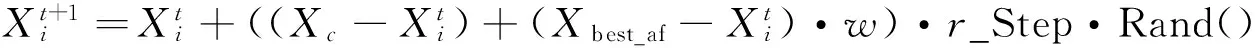
否则执行随机行为.

3.1.3追尾行为

否则执行随机行为.

3.1.4随机行为

随机行为是在其视野范围内随机选取一个位置,然后向该方向移动.其实,它是觅食行为的一个缺省行为.

3.2算法基本流程

根据多目标搜索算法原理，本文改进算法的基本流程如下.

Step1:初始化人工鱼初始位置以及人工鱼的相关参数,计算每条人工鱼的适应度值,初始筛选非劣解.

Step2:在非劣解集中随机选取人工鱼作为全局最优人工鱼,并记录全局最优的人工鱼的状态,计算w.

Step3:对每条人工鱼进行行为评价,对其要执行的行为进行选择,包括觅食、聚群、追尾和随机行为.

Step4:执行人工鱼选择的行为,基于全局信息和局部信息更新人工鱼的位置信息.

Step5:更新全局最优人工鱼的状态.

Step6:如果达到最大迭代次数,则更新人工鱼位置，否则跳转到Step3.

Step7:根据新人工鱼和当前最优人工鱼的支配关系,更新个体最优人工鱼位置,即当两条人工鱼存在支配人工鱼时,选择支配人工鱼,否则从中随机选取一条人工鱼作为新的个体最优人工鱼.

Step8：非劣解筛选.

Step8.1:合并新非劣解集和旧非劣解集,获取新的非劣解集；

Step8.2:根据非劣解集中的支配关系,筛选出新的非劣解集.

Step9:如果达到最大迭代次数,则输出最优解,否则转到Step2.

4　数值实验

4.1编码方式

4.2数值算例

算法用Matlab7.0编程,在PC机上运行,参数设定为Tmax=2000、N=50、Try_number=50、δ=25、Visual=10、Step=1.5、w1=10、w2=1.5.最大值与最小值问题可以互相转换,为了能直观地评价解质量,把求背包内物品的总体积最小问题转化为求总体积最大问题,即总体积公式变为

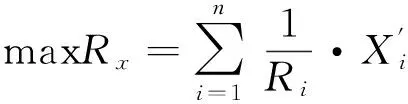
算例1取10类物品,每类物品包含5种物品,分别在[1,30],[0,1]和[1,30]中随机生成物品的价值、体积和质量,c取162.实验结果如图1和图2所示.

算例2取20类物品,每类物品包含5种物品,分别在[1,30]，[0,1]和[1,30]中随机生成物品的价值、体积和质量,c取325.实验结果如图3和图4所示.

5　实验结果

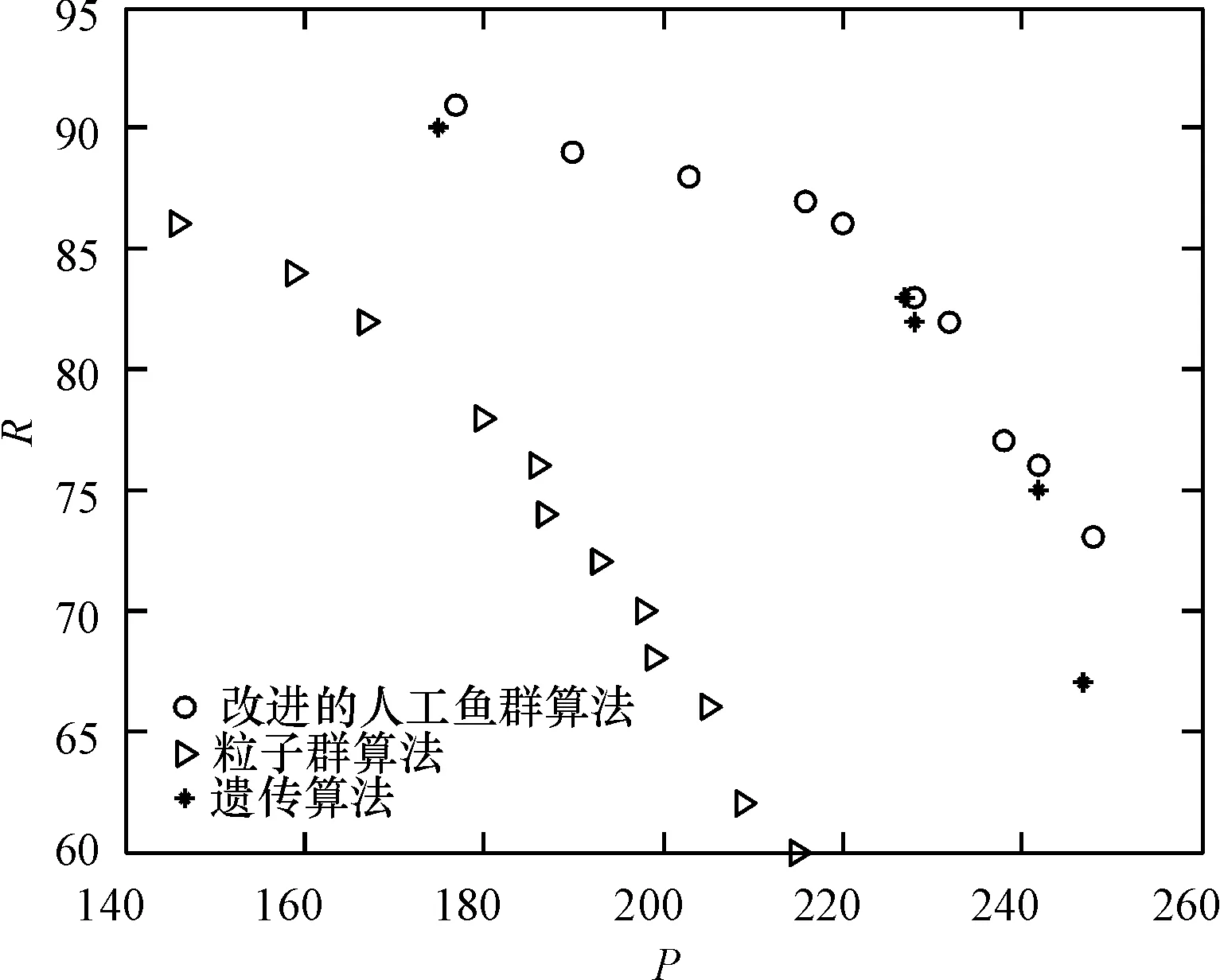
图1　算例1各算法获得的非劣解分布情况

Fig.1Non-dominated distribution of each algorithm of example 1

图2　算例1各算法非劣解平均距离曲线

Fig.2Average distance curve of the non-dominated solutions of each algorithm of example 1

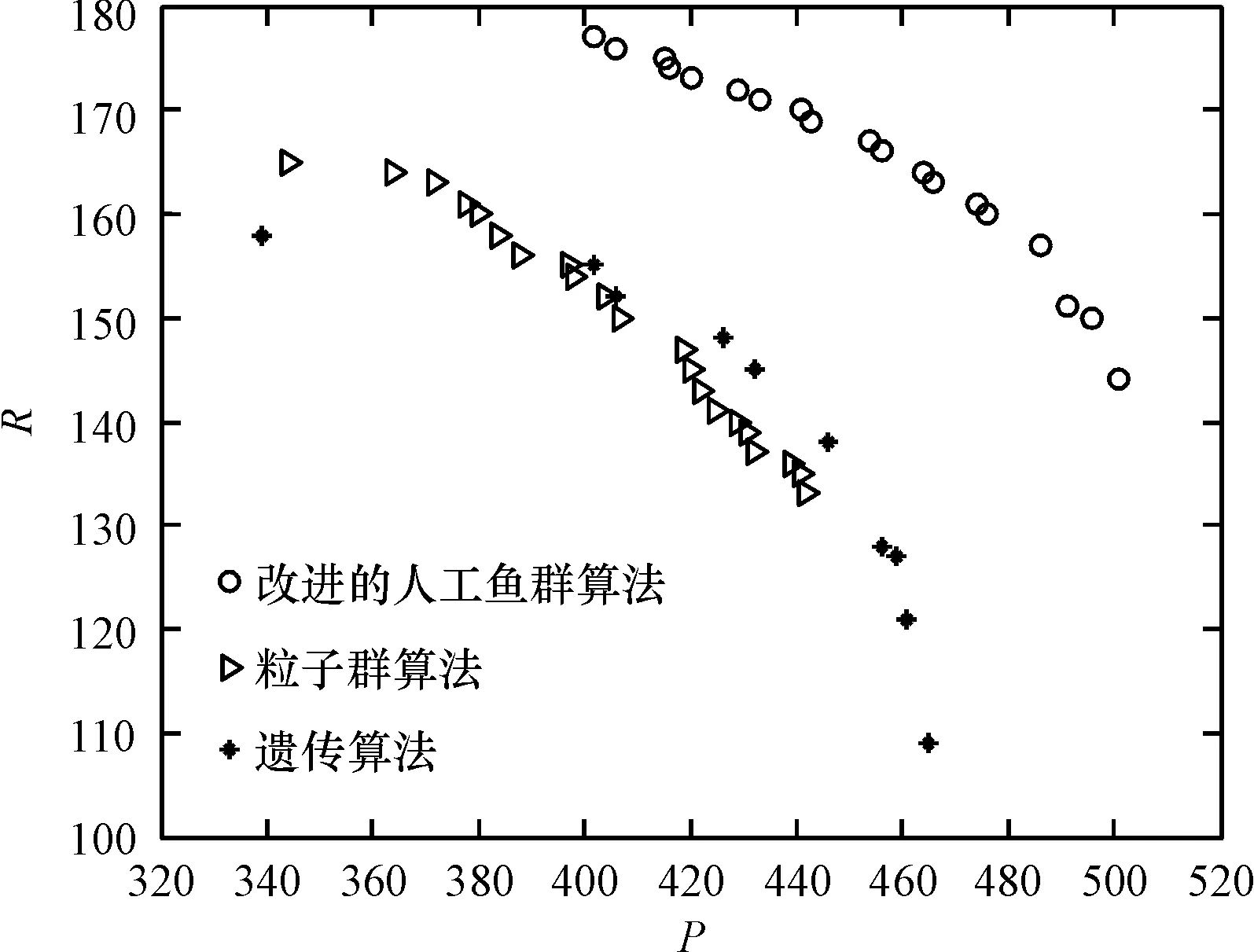
图3　算例2各算法获得的非劣解分布情况

Fig.3Non-dominated distribution of each algorithm of example 2

图4　算例2各算法非劣解平均距离曲线

Fig.4Average distance curve of the non-dominated solutions of each algorithm of example 2

对于本文中的多目标背包问题,每个算法独立运行10次,每次运行,3个算法的初始种群都是相同的,并迭代2 000次,实验结果随机取其中一次.

由图1，图3可以看出,实验结果获得的Pareto最优前端在以目标空间坐标原点为球心的超球面上,非劣解离原点越远,解的精度越高.因而,采用文献[3]中的评价方法,根据某一次迭代后获得的所有非劣解到原点的距离算术平均值来评价该次迭代的求解精度,再利用平均距离的变化趋势来评价算法的收敛性.

物品种类为10,如图1所示,本文算法与遗传算法搜索到的解基本在一个球面上,解离原点的距离比粒子群算法远,且本文搜索到的解比遗传算法的多.如图2所示,本文算法的收敛速度比另外两个算法快,解比较稳定.

当物品种类为20,如图3所示,本文算法搜索到的解与原点距离远远大于另外两个算法,且分布均匀.如图4所示,本文算法的收敛速度,解的精度、稳定性和均匀的优势更加明显.

6　结语

本文提出一种基于自适应移动策略,加入位置全局最优信息的人工鱼群算法,并用其求解多目标背包问题.仿真结果表明,本文改进的人工鱼群算法在求解多目标背包问题上是有效的,收敛速度和求解精度均优于遗传算法和粒子群算法.随着多目标背包问题中物品种类增加一倍,本文算法的优势更加明显.

[1] 史峰,王辉,胡斐，等.MATLAB智能算法30个案例分析[M].北京：北京航空航天大学出版社,2011.

[2] 张雁,肖伟.基于禁忌粒子群求解多目标0-1背包问题研究与实现[J].软件导刊,2012,11(3):36-37.

ZHANG Y, XIAO W. The Research and implementation of multiple knapsack problem on Tabu PSO[J].Software Guide, 2012, 11(3): 36-37.

[3] 郭观七,杨观赐,黄韬,等.用遗传算法求解多目标0/1背包问题[J].湖南理工学院学报,2004,17(4):18-21.

GUO G Q, YANG G C, HUANG T, et al. Solving multi-objective 0/1 knapsack problems by genetic algorithms[J].Journal of Hunan Institute of Science and Technology: Natural Sciences Edition, 2004, 17(4): 18-21.

[4] 温金宝,蔡延光.基于自适应小生境遗传算法的物流配送路径优化研究[J].广东工业大学学报,2011,28(1):20-23.

WEN J B, CAI Y G. On the optimization of logistics distribution route based on self-adaption nice genetic algorithm[J].Journal of Guangdong University of Technology, 2011, 28(1): 20-23.

[5] 李枝勇,马良,张慧珍.蝙蝠算法在多目标背包问题中的应用[J].计算机仿真,2013,30(10): 350-353.

LI Z Y, MA L, ZHANG H Z. Application of bat algorithm in multi-objective and multi-choice knapsack problem[J].Journal of Computer Simulation, 2013,30(10): 350-353.

[6] 刘海林,刘永清.多目标最优进化算法中适应性的选择[J].广东工业大学学报,2002,19(1): 7-10.

LIU H L, LIU Y Q. The fitness selection about evolutionary algorithms for multi-objective optimization[J]. Journal of Guangdong University of Technology, 2002, 19(1): 7-10.

[7] 李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式:鱼群算法[J].系统工程理论与实践,2002,22(11):32-38.

LI X L, SHAO Z J, QIAN J X. An optimizing method based on autonomous animats: fish-swarm algorithm[J]. Systems Engineering-Theory & Practice, 2002, 22(11): 32-38.

[8] 王翠茹,周春雷,马建伟.一种改进的人工鱼群算法及其在软件可靠性优化中的应用[J].计算机研究与发展,2005,4(增刊): 163-166.

WANG C R, ZHOU C L, MA J W. An Improved artificial fish-swarm algorithm and its application in software reliability optimization[J].Journal of Computer Research and Development, 2005, 4 (S):163-166.

[9] 程永明.群智能优化算法及其在通信中的应用研究[D].济南:山东大学信息科学与工程学院,2010.

[10] JIANG M Y, YUAN D F, CHENG Y M. Improved artificial fish swarm algorithm[C]∥Proceedings of the 5th International Conference on Natural Computation. Tianjin: IEEE: 2009: 281-285.

[11] 王联国,洪毅,施秋红.全局版人工鱼群算法[J].系统仿真学报,2009,21(23): 7483-7486.

WANG L G, HONG Y, SHI Q H. Global edition artificial fish swarm algorithm[J]. Journal of System Simulation, 2009, 21(23): 7483-7486.

[12] 李晓磊.一种新型的智能优化方法——人工鱼群算法[D].杭州:浙江大学系统工程研究所,2003.

[13] 廖煜雷,苏玉明,张磊。一种自适应人工鱼群算法及其在无人艇控制中的应用[J].中南大学学报：自然科学版,2013, 44(10): 4109- 4116.

LIAO Y L, SU Y M, ZHANG L. Adaptive artificial fish swarm algorithm and application in control of unmanned surface vessel[J].Journal of Central South University：Science and Technology, 2013,44(10): 4109- 4116.

[14] 朱旭辉,倪志伟,程美英.变步长自适应的改进人工鱼群算法[J].计算机科学,2015,42(2): 210-216.

ZHU X H, NI Z W, CHENG M Y. Self-adaptive improved artificial fish swarm algorithm with changing step[J].Computer Science, 2015, 42(2): 210-216.

[15] 马宪民,刘妮.自适应视野的人工鱼群算法求解最短路径问题[J].通信学报,2014,35(1): 1-6.

MA X M, LIU N. Improved artificial fish-swarm algorithm based on adaptive vision for solving the shortest path problem[J]. Journal on Communications, 2014, 35(1): 1-6.

[16] 江铭武,袁东风.人工鱼群算法及其应用[M].北京：科学出版社,2012.

An Improved Artificial Fish Swarm Algorithm for Multi-objective Knapsack Problem

Huang Mei-hua, Wen Jie-chang, He Yong

(School of Applied Mathematics, Guangdong University of Technology, Guangzhou 510520, China)

As a swarm intelligence, the Artificial Fish Swarm Algorithm(AFSA) has its weakness in solving the problem of Multi-objective Knapsack, such as blindness search, low speed of convergence and low accuracy in solution. Combining the global information of the artificial fish position with improving the moving strategy of artificial fish self-adapting, an improved AFSA is proposed. Simulation on multi-objective knapsack problem shows that the convergence rate as well as the accuracy in the non-dominated solutions which have been found out in the improved AFSA is superior to Genetic Algorithm and Particle Swarm Optimization.

multi-objective optimization; Knapsack problem; artificial fish swarm algorithm; self-adaptive

2015- 04- 29

广东省特色创新项目(2014KTSCX055)

黄美华(1987-)，女，硕士研究生，主要研究方向为最优化方法与应用.

10.3969/j.issn.1007- 7162.2016.05.008

F252; TP301

A

1007-7162(2016)05- 0044- 05