对不确定原理的一点新认识

孙为民

(南京大学 物理学院，江苏 南京　210093)



对不确定原理的一点新认识

孙为民

(南京大学 物理学院，江苏 南京210093)

讨论了在一维的有限区域内运动的、采用箱归一化处理的自由粒子的位置动量不确定关系的表达，发现在这样特定的物理情形下，粒子的位置坐标与动量不能同时测准的物理论断虽然一定成立，但通常的位置动量不确定关系的数学表达形式需要作一定形式的修改， 本文得出了这一情形中位置动量不确定关系的具体形式，由此加深了对于量子力学中的不确定原理的认识，并且从对箱归一化下的自由粒子的动量不确定度的认识的角度出发，讨论了对于无穷体积极限的物理认识.

不确定关系；周期性边界条件；无穷体积极限

在通常国内的量子力学教材中，对于不确定原理的讲授是通过直接分析算符的数学形式和对易关系给出的(例如见文献[1])，这样的分析与推导是足够普遍的，但就物理问题本身而言，并未包括全所有的物理上感兴趣的情形.这样的情形的一个简单例子，就是在有限区域内运动的，采用箱归一化处理的自由粒子的情形.本文就试图以此具体情形为例，讨论一下这种情形下不确定关系的具体表达，以及如何看待“无穷大体积”极限这一物理问题.

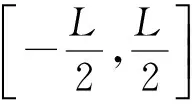
(1)

系统的任一波函数(指满足周期性边界条件的波函数)都可表示为这一组动量本征函数的线性叠加：

(2)

现在我们来计算一下在这样的一个波函数所描述的状态下粒子的动量不确定度 Δp和位置不确定度Δx.假定波函数已归一化，则有

(3)

(4)

于是得出

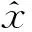
(6)

(7)

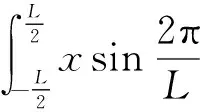
(8)

此处涉及到的积分通过直接计算可给出

(9)

由此算出

(10)

这样立即就有

(11)

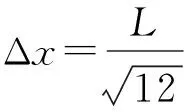
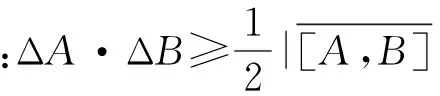
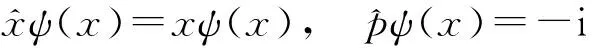
(12)

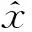
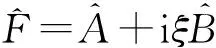
(13)

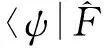
可得出

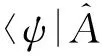
(14)

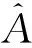
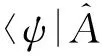
(15)

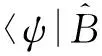
(16)

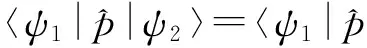
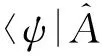
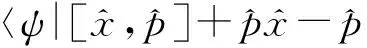
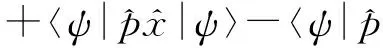
(17)

通过直接计算给出：

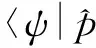
(18)

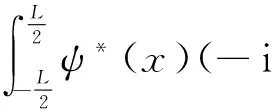
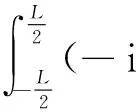
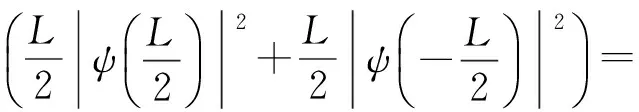
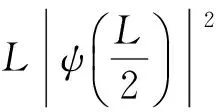
(19)

在得出上式最后一步时，用到了所讨论的ψ(x) 满足周期性边界条件这一点.从上面的结果出发，利用式(14)就能得出

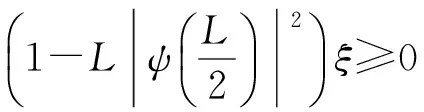
(20)

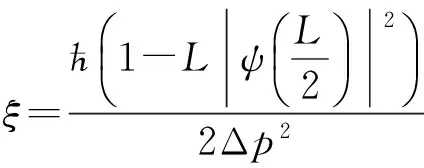
(21)

这样就有

(22)

或者写为

(23)

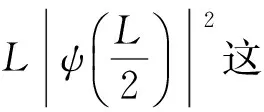
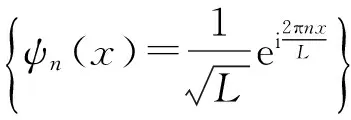
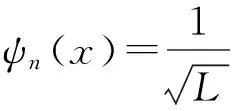
[1]钱伯初. 量子力学[M]. 北京：高等教育出版社, 2006: 94-98.

Some new cognitions for the uncertainty principle

SUN Wei-min

(School of Physics, Nanjing University, Nanjing, Jiangsu 210093, China)

This paper discusses the expression of the position-momentum uncertainty relation for the case of a free particle moving in a one-dimensional finite region, which is subjected to the box normalization treatment. It is found that for such a specific physical situation, although the physical thesis that the position coordinate and the momentum of a particle cannot be exactly measured simultaneously certainly holds, the mathematical form of the usual position-momentum uncertainty relation needs some modifications. In this paper the concrete form of the position-momentum uncertainty relation for such a situation has been obtained, which deepens our understanding of the uncertainty principle in quantum mechanics. From the viewpoint of the cognition of the momentum uncertainty of a free particle subjected to the box normalization, a discussion of the physical cognition of the infinite volume limit is also made.

uncertainty relation; periodic boundary condition; infinite volume limit

2015-05-07；

2015-07-20

孙为民，(1973—)，男，江苏苏州人，南京大学物理学院现代物理系副教授，博士，主要从事量子规范场论的形式理论的研究工作.

O 413.1

A

1000- 0712(2016)02- 0011- 03