夫琅禾费衍射的线性变换计算
张文玉,戴又善
(浙江大学 城市学院,浙江 杭州 310015)
夫琅禾费衍射的线性变换计算
张文玉,戴又善
(浙江大学 城市学院,浙江 杭州310015)
夫琅禾费衍射在二维小孔的线性变换下具有简单的变换特性,利用线性变换的方法简便求得了位于坐标系中任何位置的任意三角形小孔和任意平行四边形小孔夫琅禾费衍射复振幅的一般解析表达式,从而提供了一种普遍的方法,无需通过积分计算而仅由代数运算来求得任意多边形小孔夫琅禾费衍射光强分布的解析表达式.作为应用例子讨论了正六边形小孔夫琅禾费衍射的光强分布,并依据所得解析结果进行了计算机模拟.
夫琅禾费衍射;线性变换;三角形小孔;平行四边形小孔;正六边形小孔
二维小孔的衍射问题通常是基于基尔霍夫衍射公式来讨论[1],但基尔霍夫衍射公式的数学运算比较复杂,在讨论具体问题时也常需做各种计算近似,这导致对许多典型小孔的衍射通常并不能给出简明的解析结果而是求助于近似数值计算[2,3].由于夫琅禾费衍射是一种远场衍射,其入射光和衍射光都为平行光,这使得夫琅禾费衍射既能反映出衍射的一些基本特征,又具有特殊的简单性. 研究夫琅禾费衍射的复振幅(以下简称振幅)和光强分布通常需要进行二维复积分计算,特别是对于复杂几何图形的小孔衍射,计算将变得更为冗长.而利用小孔的几何对称性来讨论二维小孔夫琅禾费衍射问题将可以极大的简化计算,对此我们在先前文献中已讨论过小孔的某些对称变换特性[4,5].本文则将进一步通过一般线性变换的方法,利用统一的线性变换矩阵来讨论小孔的几何对称变换,从而可以在避开复杂的基尔霍夫衍射公式计算的情况下,提供一种无需积分计算而仅通过代数运算来解析求得各种二维小孔夫琅禾费衍射振幅和光强分布的普遍方法.
任何由直线构成的几何小孔都可以分解为若干个三角形小孔,或者分解为若干个三角形小孔和平行四边形小孔的组合(平行四边形小孔和三角形小孔都具有3个独立坐标顶点,由于平行四边形小孔相比于三角形小孔更具有对称性,因
而其衍射振幅的公式将更为简单).虽然计算给定的三角形小孔和平行四边形小孔的衍射振幅并不太难,但分解多边形小孔则需要确定任何位置和任意形状的三角形小孔和平行四边形小孔,因此研究任意三角形小孔和任意平行四边形小孔的衍射就构成了研究一般多边形小孔衍射的基础.利用二维小孔在线性变换下夫琅禾费衍射振幅的变换特性,则无需再进行具体积分运算就可求得变换后相应小孔夫琅禾费衍射的振幅和光强分布.为此本文首先计算了一个最简单基本的等腰直角三角形小孔的夫琅禾费衍射,然后通过对该小孔的适当线性变换,简便求得了位于坐标系中任何位置的任意三角形小孔的夫琅禾费衍射振幅公式;另外通过计算一个最简单基本的正方形小孔的夫琅禾费衍射,同样通过对该正方形小孔的适当线性变换,简便求得了位于坐标系中任何位置的任意平行四边形小孔的夫琅禾费衍射振幅公式.需要指出的是由于衍射振幅中三角函数的表达形式并不是唯一的,采用不同的积分过程得到的衍射振幅在表达形式上也将是不相同的,但通过选取适当线性变换的方法能够非常简便地寻求到衍射振幅最简单的解析表达形式,从而利用本文提供的小孔线性变换的方法和计算结果,原则上无需再进行积分计算而仅由代数运算就能够给出任意多边形小孔夫琅禾费衍射振幅和光强分布的一般解析表达式.
1 夫琅禾费衍射振幅与线性变换
对于二维小孔的夫琅禾费衍射,观察屏上的任一点P,其衍射角可以用两个参数来描写,不妨取为θx和θy,如图1所示(图中省略未画出起会聚平行光作用的凸透镜).由图2及文献[5],给出了二维小孔的夫琅禾费衍射复振幅(以下简称振幅)为
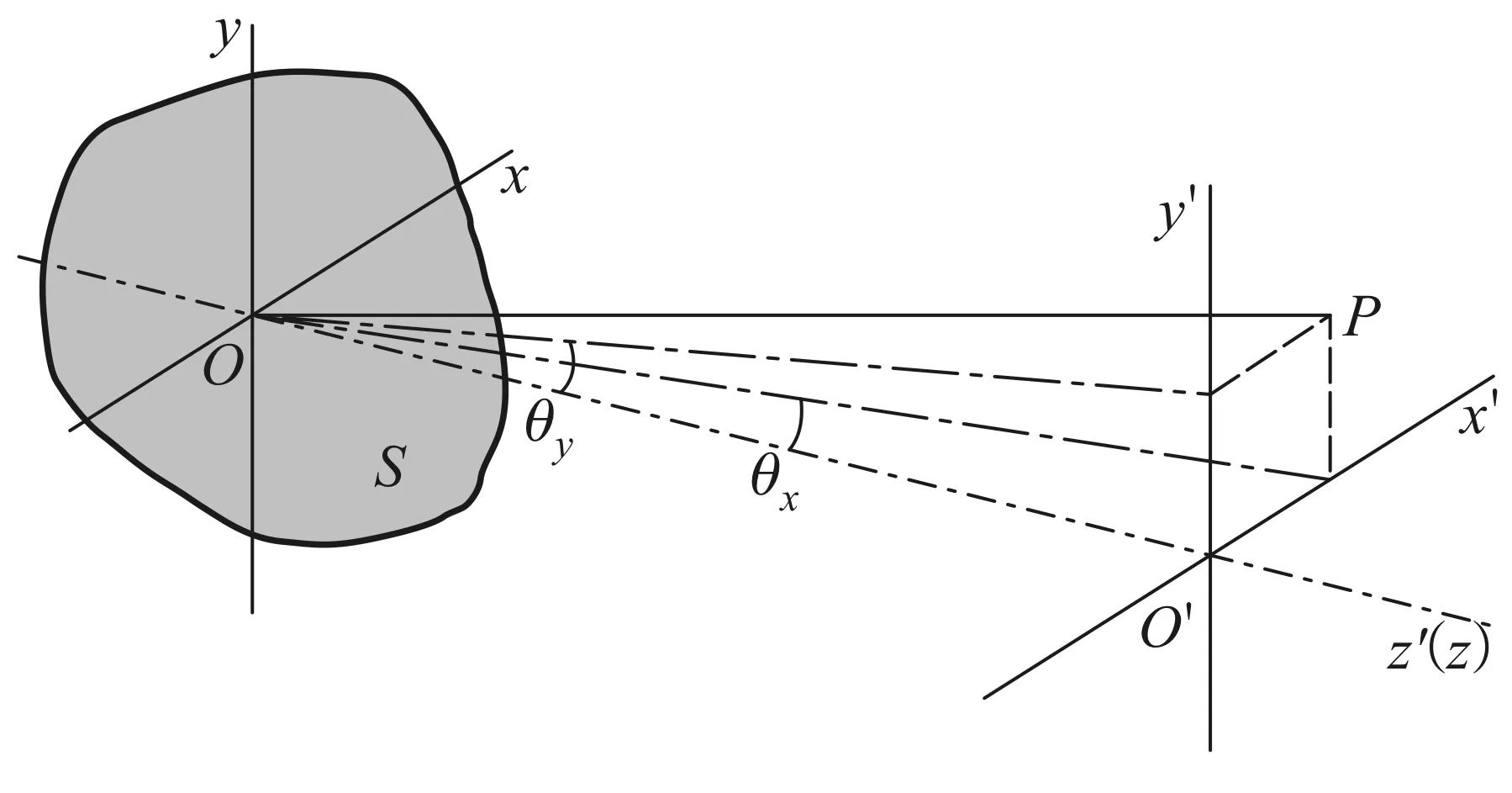
图1 夫琅禾费小孔衍射
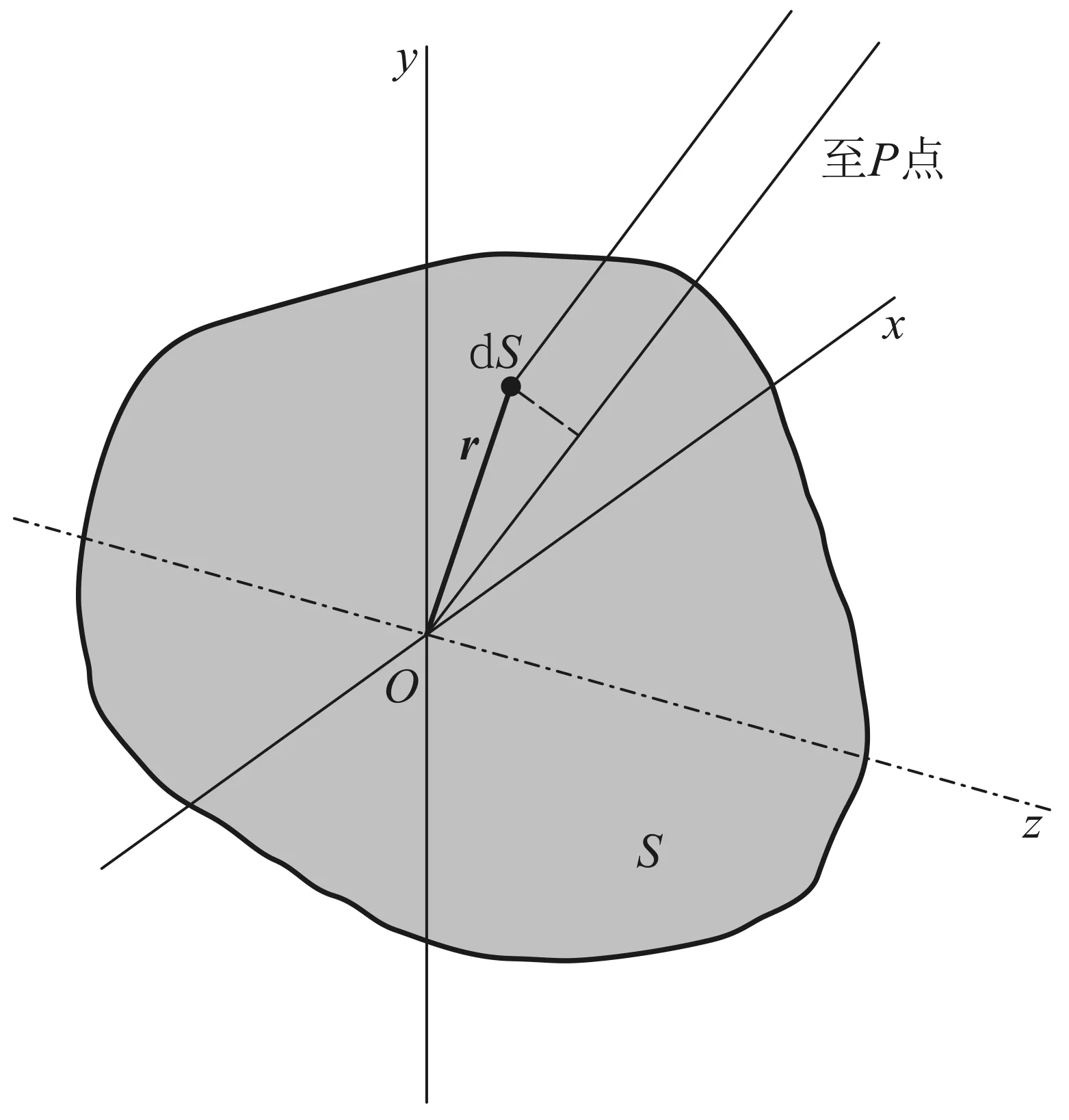
图2 夫琅禾费衍射光程差
(1)
上式中
(2)
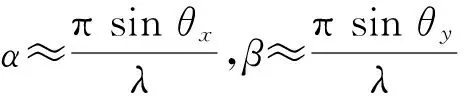
若对二维小孔S作一般的线性变换,变成新的小孔S′
(3)
令r′=x′i′+y′j′,r=xi+yj,r0=x0i+y0j,即有
(4)
小孔面积元的变换为
dS′=dx′dy′=|J|dxdy=|J|dS
(5)
其中J为相应线性变换的雅可比行列式,对于线性变换其值为常数
(6)
则小孔面积变换为
S′=∫dS′=∫|J|dS=|J|∫dS=|J|S
(7)
设原小孔S的衍射振幅为E(α,β),经线性变换后的小孔S′的衍射振幅为E′(α,β),则有
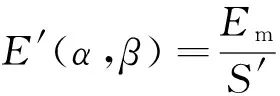
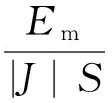
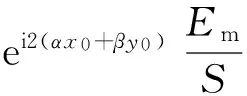
(8)
即有
(9)而对于r0=0的齐次线性变换,则有E′(α,β)=E(α′,β′)=E(aα+cβ,bα+dβ).以上我们给出了二维小孔在一般线性变换下夫琅禾费衍射振幅的变换特性公式,下面讨论几种常见的线性变换特例.1) 旋转变换
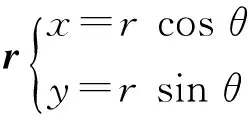
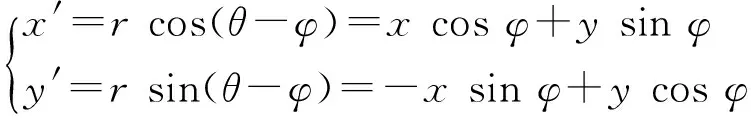
(10)
引进旋转变换矩阵
(11)
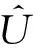
E(αcosφ-βsinφ,αsinφ+βcosφ)
(12)
2) 平移变换
对小孔S的位置整体进行平移r0=x0i+y0j,平移变换后的小孔矢径为r′=r+r0,则U=I;平移后小孔S′的衍射振幅为
E′(α,β)=ei2(x0α+y0β)E(α,β)
(13)
由于光强正比于振幅模的平方,因此对小孔的整体平移并不改变衍射的光强分布|E′(α,β)|2=|E(α,β)|2.
3) 拉伸变换
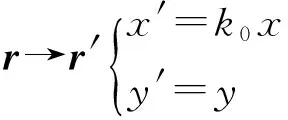
(14)
拉伸变换后小孔S′的衍射振幅为
(15)

若考虑拉伸方向与x轴的夹角为φ,拉伸幅度为k0(为常数),相应的拉伸变换矩阵为
Uφ(k0)=UR(-φ)Ux(k0)UR(φ)=
(16)
则拉伸变换后小孔S′的衍射振幅
(17)
其中
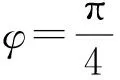
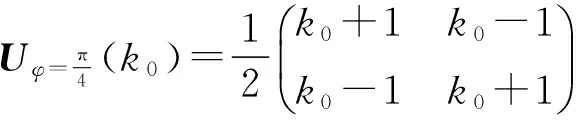
(19)
4) 放大(缩小)变换
(20)
放大(缩小)变换后小孔S′的衍射振幅为
(21)放大(缩小)变换相当于同时对x方向和y方向进行相同比例的拉伸变换,k0=-1则为空间反演变换.
2 任意三角形小孔的夫琅禾费衍射

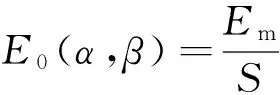
(22)

图3 等腰直角三角形小孔的衍射
对于处在坐标系中任何位置和任意形状的三角形小孔,设其3个顶点的坐标分别为A(x0,y0)、B(x1,y1)、C(x2,y2),其衍射振幅记为E△(α,β);先将顶点A(x0,y0)平移到坐标原点,则三角形3个顶点的坐标将分别变为A′(0,0)、B′(x1-x0,y1-y0)、C′(x2-x0,y2-y0),见图4.设其衍射振幅为E′(α,β),则有

图4 任意三角形小孔的衍射
(23)
选择线性变换矩阵U,满足
(24)
(25)
即可具体确定相应的线性变换矩阵为
(26)
则有
(27)
上式中
(28)
由式(23)、(27)和基本等腰直角三角形小孔的衍射振幅式(22)可得任意三角形小孔的夫琅禾费衍射振幅为
(29)

(30)
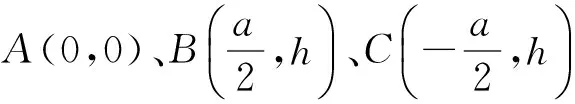
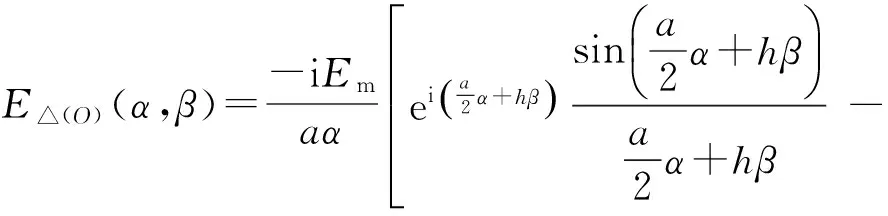
(31)
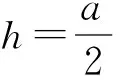
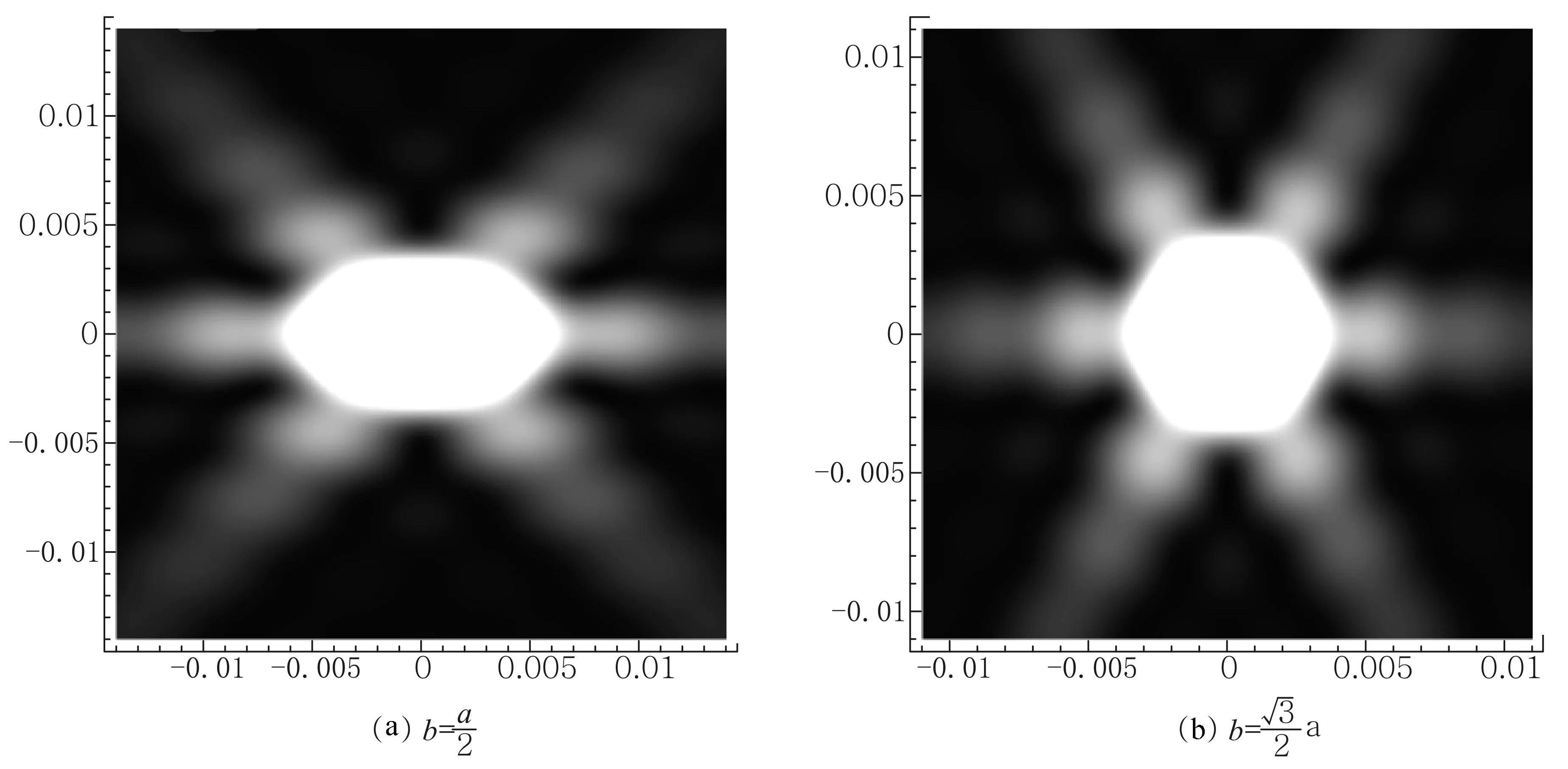
图6 等腰和等边三角形小孔的夫琅禾费衍射计算机模拟
3 任意平行四边形小孔的夫琅禾费衍射
首先计算一个最简单的基本平行四边形小孔即正方形小孔的衍射振幅E0(α,β),设正方形小孔的边长都为单位长度1,小孔的面积为S=1,如图7所示,则有
图7 正方形小孔的衍射
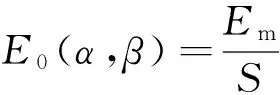
(32)
对于处在坐标系中任意位置和任意形状的平行四边形小孔,设其四个顶点的坐标分别为A(x0,y0)、B(x1,y1)、C(x2,y2)、D(x3,y3),其衍射振幅为E▯(α,β);先将顶点A(x0,y0)平移到坐标原点,则平行四边形四个顶点的坐标将分别变为A′(0,0)、B′(x1-x0,y1-y0)、C′(x2-x0,y2-y0)、D′(x3-x0,y3-y0),见图8.设其衍射振幅为E′(α,β),则有

图8 任意平行四边形小孔的衍射
(33)
选择线性变换矩阵U,满足
(34)
(35)
即可具体确定相应的线性变换矩阵为
(36)
因为对于平行四边形有关系式x3+x0=x1+x2, y3+y0=y1+y2, 即平行四边形4个顶点只有3个顶点的坐标是独立的,则有
(37)
由此可知,线性变换矩阵U可将方孔变换到所求的平行四边形小孔,则有
(38)
由式(33)、(38)和基本正方形小孔的衍射振幅式(32),可得任意平行四边形小孔的夫琅禾费衍射振幅为
E▯(α,β)=ei2(x0α+y0β)E0(α′,β′)=
(39)
代入α′、β′的表达式
(40)
可得
E▯(α,β)=Emei[(x1+x2)α+(y1+y2)β]·
(41)
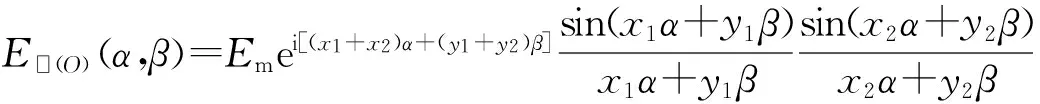
(42)
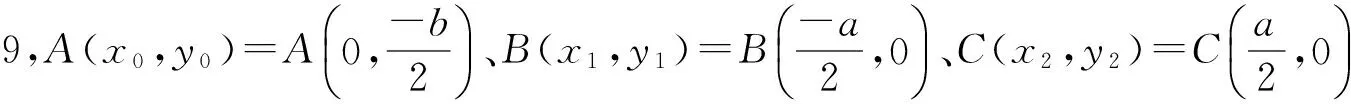
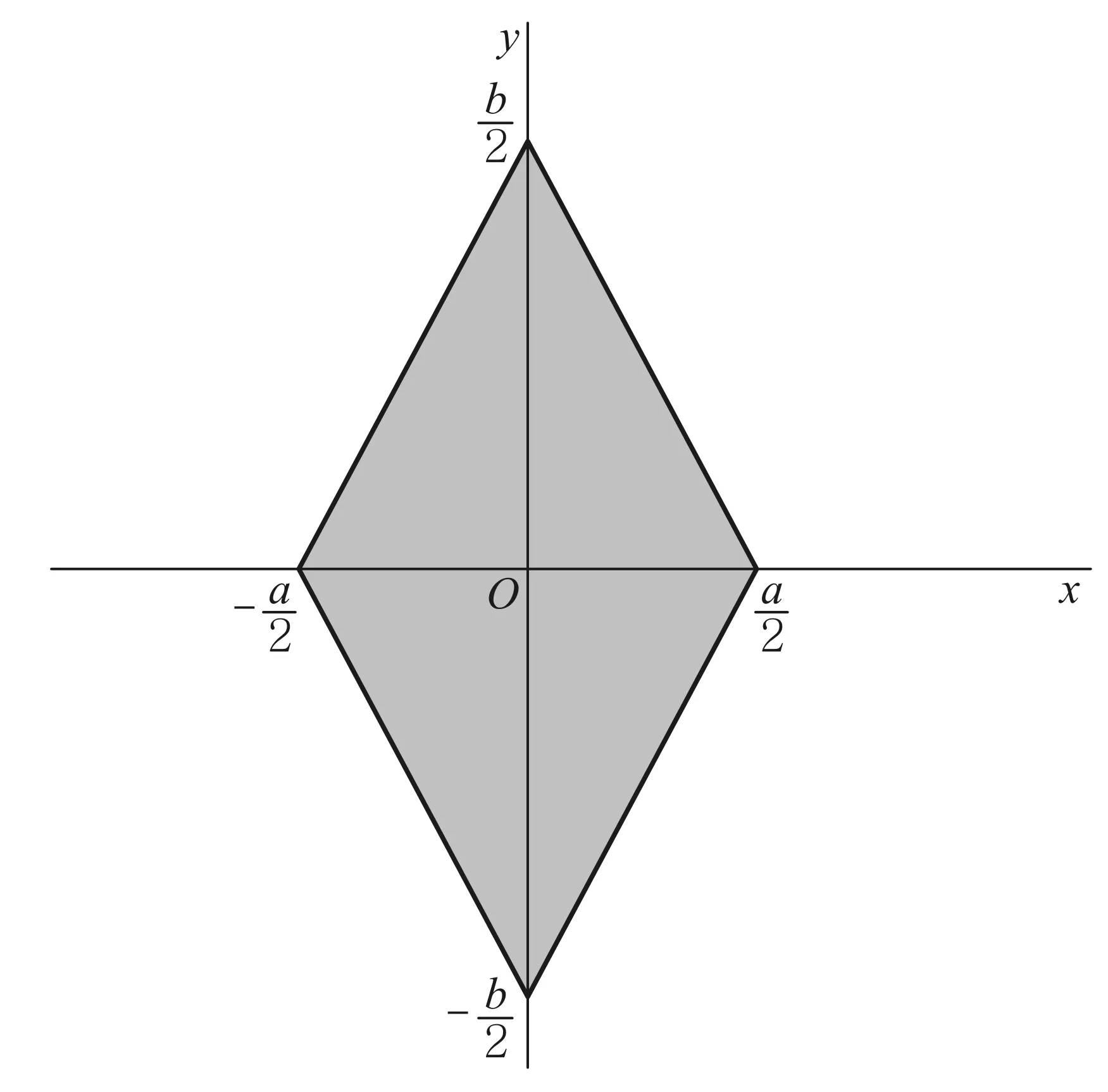
图9 菱形小孔的衍射
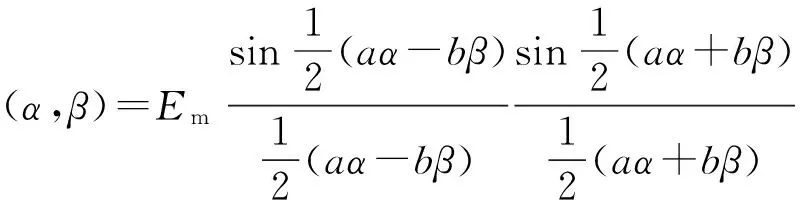
(43)
(44)
图10为旁轴近似条件下相应于式(44)的菱形小孔夫琅禾费衍射的计算机模拟图像.其中图10(a)为b=3a的菱形小孔衍射图像;图10(b)为b=a的正菱形小孔衍射图像,即为旋转了45°的方孔衍射图像.
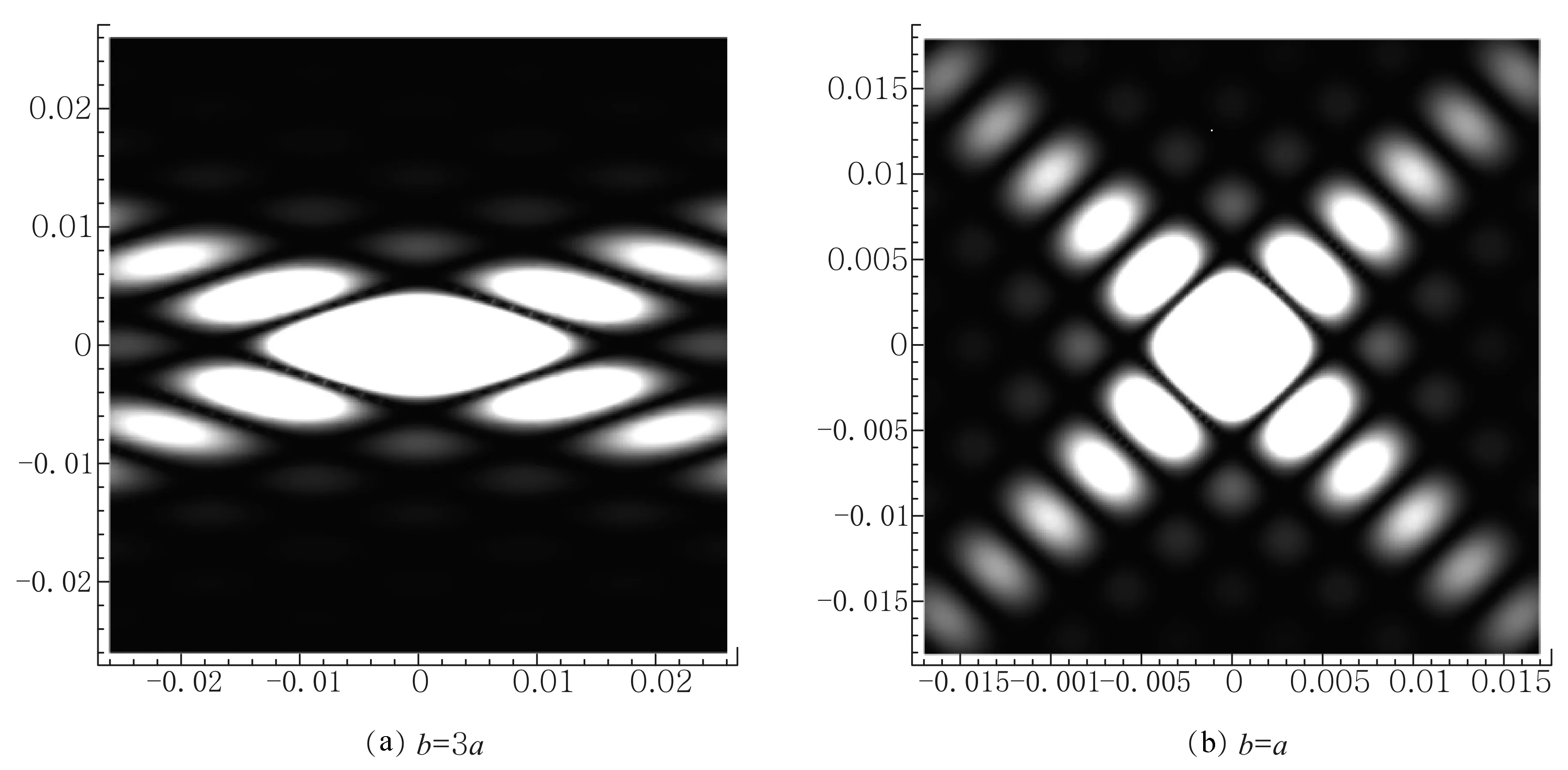
图10 菱形小孔的夫琅禾费衍射计算机模拟
4 正六边形小孔的夫琅禾费衍射
一个任意的多边形小孔总可以分解为若干个三角形小孔,而在某些情况下则可分解为若干个三角形小孔和平行四边形小孔的组合.因此求得了任意三角形小孔和任意平行四边形小孔的衍射振幅公式,原则上无需再进行积分计算仅通过代数运算就可以得到任意多边形小孔衍射振幅的解析表达式.作为一个简单的典型应用例子,本小节将讨论边长为a的正六边形小孔的夫琅禾费衍射振幅和光强分布.
利用前面已给出的衍射振幅公式,首先计算一个等腰三角形小孔(Ⅰ)和一个平行四边形小孔(Ⅱ)的夫琅禾费衍射振幅,见图11. 所选取的小孔(Ⅰ)和(Ⅱ)都是以坐标原点为顶点,且等腰三角形小孔(Ⅰ)具有相对y轴的对称性,而平行四边形小孔(Ⅱ)具有相对x轴的对称性,这样充分利用了小孔的对称性能够进一步简化衍射振幅的计算和表达式.
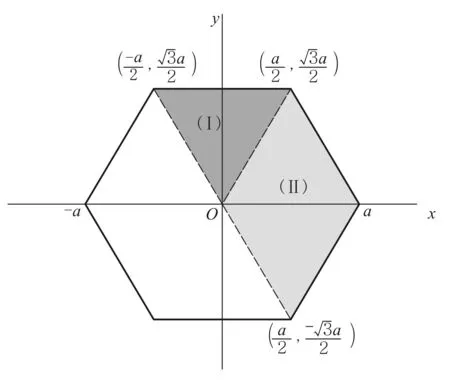
图11 正六边形小孔的衍射

(45)
上式的实部为

(46)
(47)

(49)
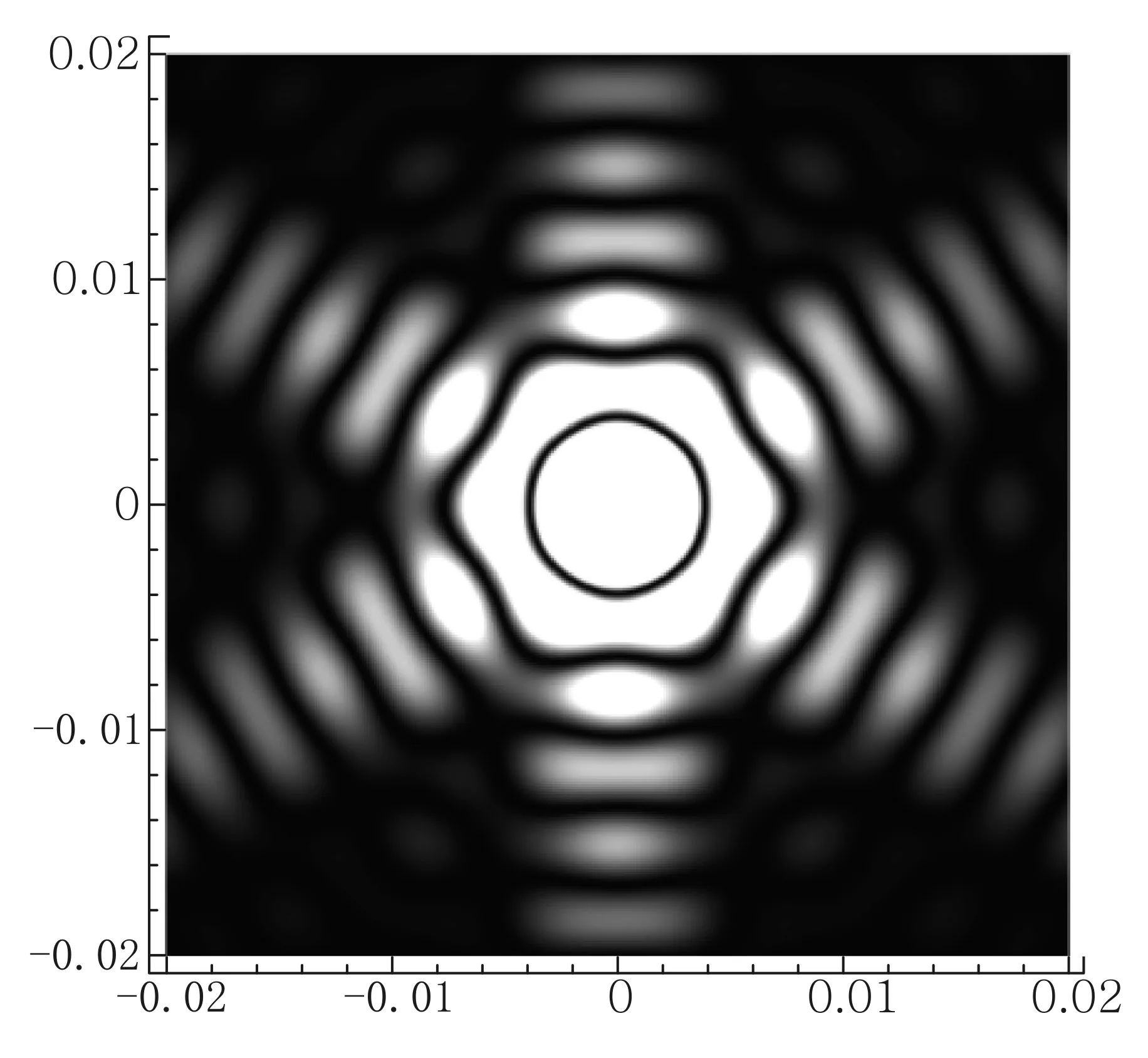
图12 正六边形小孔的夫琅禾费衍射计算机模拟
对于复杂小孔的衍射通常是通过计算机编程利用数值计算的方法来近似求解,本文则提供了一种无需积分计算的解析求解方法,而对于小孔衍射的计算机模拟由于是基于光强分布的解析表达式,因而无需特别编程就可利用Mathematica等通用数学软件对光强分布的解析公式直接进行亮度模拟,相比于完全数值求解的计算机模拟具有模拟速度快、计算精度高以及便于参数调节等显著优点,从而能够更好地直观了解各种小孔夫琅禾费衍射的光强分布特点.
本文利用二维小孔在一般线性变换下夫琅禾费衍射振幅的变换特性[见公式(9)],通过小孔线性变换的方法,给出了坐标系中处于任何位置的任意三角形小孔和任意平行四边形小孔的夫琅禾费衍射振幅公式.由于三角形和平行四边形是几何图形的构成基础,一个由直线构成的任意几何图形总可以分解为若干个三角形,或者分解为若干个三角形加平行四边形的组合(由于平行四边形小孔相比于三角形小孔具有更为简单的衍射振幅表达式),因而利用本文给出的小孔线性变换的方法和结果,提供了一种普遍的解析计算方法,原则上已无需再作积分计算而仅由代数运算就能够给出任意多边形小孔夫琅禾费衍射光强分布的一般解析表达式.而充分利用小孔的对称特性则能够进一步简化衍射振幅的计算,本文在最后小节中给出了一个正六边形小孔夫琅禾费衍射的计算应用举例,限于篇幅更多的应用将在另文中讨论.
[1]叶玉堂,绕建珍,肖峻,等. 光学教程[M].北京:清华大学出版社, 2005.
[2]戴兵,贺安之,等.一类与椭圆和矩形相关的孔径的夫琅禾费衍射研究[J].大学物理,2003,22(3) : 5-8.
[3]谢嘉宁,赵建林,陈伟成,等.夫琅禾费衍射的计算机仿真[J].大学物理,2004,23(3) : 51-54.
[4]戴又善,戴亮.推导圆孔夫琅禾费衍射光强分布的一种简便方法[J].大学物理,2009,28(4) : 29-32.
[5]戴又善.二维小孔的对称变换与夫琅禾费衍射光强分布[J].大学物理,2011,30(11) : 22-27.
Calculate of Fraunhofer diffraction by linear transformation
ZHANG Wen-yu, DAI You-shan
(Zhejiang University City College, Hangzhou, Zhejiang 310015, China)
Fraunhofer diffraction transforms in a simple way under a linear deformation of the shape of the two-dimensional aperture. Based on simple linear transformation, we derive general analytic expressions for the diffraction amplitude in the case of triangular and rhomboidal apertures of arbitrary shape at any given position in a coordinate system. Without performing integration, we solve the Fraunhofer diffraction by any polygon aperture of any shape, through purely algebraic operations. As an example, we apply the present method to find the diffraction intensity distribution for a regular hexagon aperture, and simulate it on a computer based on our analytical results.
Fraunhofer diffraction;linear transformation;triangle aperture;parallelogram aperture;regular hexagon aperture
2015-07-15;
2016-03-24
浙江大学城市学院大学生科研课题(X2016521006)资助
张文玉(1994—),女,四川成都人,浙江大学城市学院计算分院2013级本科生.
O 436.1
A
1000- 0712(2016)07- 0047- 09

