椭圆偏振光转换为圆偏振光的琼斯矩阵分析及实验研究
王 超,江 伦,董科研,安 岩,姜会林
(1. 长春理工大学 空间光电技术国家地方联合工程研究中心,吉林 长春 130022;2. 长春理工大学 空地激光通信技术重点学科实验室,吉林 长春 130022 )
椭圆偏振光转换为圆偏振光的琼斯矩阵分析及实验研究
王超1,2,江伦1,2,董科研1,2,安岩1,2,姜会林1,2
(1. 长春理工大学 空间光电技术国家地方联合工程研究中心,吉林 长春130022;2. 长春理工大学 空地激光通信技术重点学科实验室,吉林 长春130022 )
应用琼斯矩阵,推导出了利用单波片或一对级联的1/4波片将椭圆偏振光转化为圆偏振光时,波片应具有的参量.针对级联波片方案,定量地分析了第一块或第二块波片各自存在旋转角度误差时对出射光偏振态造成的影响,并设计了实验进行验证.
椭圆偏振光;圆偏振光;琼斯矩阵;波片
按照光矢量端点轨迹形成图形的不同,偏振光可分为线偏振光、圆偏振光和椭圆偏振光.许多物理光学教材上均给出了线偏振光转化为圆偏振光(或椭圆偏振光)的方法,即利用1/4波片,且波片的快轴与入射线偏振光的矢量成特定的角度,但通常直接给出结论,缺少相应的推导过程[1,2].大学物理实验中关于偏振的部分一般也只有检验光束的偏振态以及验证马吕斯定律等[3],对于多种偏振态之间的转化缺乏直观的实验演示.
在实际应用中,往往有着将椭圆偏振光转化为圆偏振光的需求.例如空地激光通信中,一般要求信号以圆偏振光为载体进行传输[4].激光通信的发射端由半导体激光器和光学系统组成,激光器出射的光束通常接近完全线偏振光,其通过光学系统时,由于光路中存在一些45°放置的反光镜、分光片等,其上镀制的膜系造成p光和s光产生的相位延迟不一致,使得光束偏振态转化为椭圆偏振光.此时必须在光路中进行偏振补偿,使得最终从发射天线出射的为圆偏振光.
基于以上教学和科研中遇到的实际问题,本文进行了椭圆偏振光转换为圆偏振光的理论分析及相关实验验证.采用琼斯矩阵推导了使用单波片或一对级联的1/4波片两种方案进行转换时,波片应具有的参量;针对级联波片方案,分别分析了第一块或第二块波片存在旋转角度误差时对出射光偏振态造成的影响,并设计了实验进行验证.这些理论分析与实验内容是目前物理光学课程偏振部分的有益补充,意在使学生更深入地理解各种偏振态之间转化的原理,掌握转化的实验方法,并有助于培养学生解决实际科研问题的能力.
1 椭圆偏振光通过单个波片变换为圆偏振光
对于任意完全偏振光,其琼斯矩阵可表示为
(1)
其中a为偏振光两分量的振幅比,Δφ为两分量的相位差.为了简化问题,我们设定坐标系的x轴与椭圆轨迹的主轴重合,则椭圆偏振光的矩阵表示为
(2)
其中,x轴与长轴重合时,a<1;x轴与短轴重合时,a>1.
我们的目的是使该椭圆偏振光通过快轴与偏振长轴呈一定角度摆放,且快、慢轴间具有一定相位延迟量的波片后,变为圆偏振光.一个快轴与x轴夹角为θ,快、慢轴间的相对相位延迟为δ的波片,其琼斯矩阵可写为[1]
(3)
则椭圆偏振光通过该波片后,新的偏振态可表示为
E1=GE0
(4)
将式(2)、(3)代入式(4)并整理,得到
(5)
(6)


(7)
(8)
δ设定为快、慢轴间相位差,其值恒为正值,可知
(9)
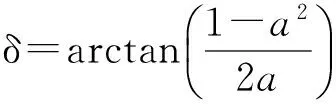

2 椭圆偏振光通过一对级联波片变换为圆偏振光
1/4波片是普物实验室常见的光学器件,其产生的延迟量为π/2.文献[1]已给出结论:单个1/4波片可将椭圆偏振光转化为线偏振光,或将线偏振光转化为圆偏振光,下面由此结论,利用琼斯矩阵反推得到这两种结果时波片需满足的条件.
2.1椭圆偏振光转换为线偏振光
由式(3),1/4波片的琼斯矩阵为
(10)
则椭圆偏振光通过1/4波片后,其偏振态的琼斯矩阵可写作(省略了整个矩阵前的常数系数):
(11)
若E21为线偏振光,则应满足
(12)
设E21x的辐角为a1,E21y的辐角为a2.则根据式(11)、(12)得到
(13)
(14)
tana1=tana2
(15)
将式(13)、(14)代入式(15)并整理,得到
(a2-1)sin 2θ=0
(16)
一般情况下,椭圆偏振光振幅比|a|≠1,要使式(16)成立,只有令sin 2θ=0,即θ=0或±π/2.可知第一个1/4波片的快轴必须平行于椭圆偏振光的长轴或短轴放置,出射即为线偏振光.
2.2线偏振光转换为圆偏振光
为讨论方便,重新设定坐标系,令y轴与第一波片出射线偏振光的光矢量方向重合.即线偏振光的偏振态可写为
(17)
令该光束再次通过快轴与目前的x轴成θ角的1/4波片,则最终得到的出射光偏振态为(同样省略了整个矩阵前的常数系数)
(18)
易知要使E2为圆偏振光,必须满足两分量振幅比为1,相位差为90°的条件,即
(19)
1+2cos 2θ+cos22θ-sin22θ=0
(20)
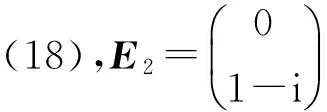
3 波片旋转角度误差对出射光偏振态的影响
实际使用中,波片一般装在旋转架上,靠手动旋转波片来调整其快轴方向.这种手调方式精度较低,使得波片快轴方向与理论值存在一定误差.从上一节分析可知,这将影响出射光的偏振态.假设能够直接观察从第一个或第二个波片出射光的偏振态,最直观的现象应是出射光光矢量末端的运动轨迹不再是完美的直线或圆,而是向椭圆的方向发展.下面将定量地分析这种旋转角度偏差与出射光偏振态改变量之间的关系,以光矢量轨迹的离心率为量度.
3.1第一个1/4波片的旋转角度误差对出射光偏振态的影响
设旋转造成快轴方向角度与理想值的误差为Δθ.则椭圆偏振光通过该波片后,其偏振态矩阵为

(21)
由2.1节可知理论值θ=0或±π/2,首先考虑θ=0的情况,则有
(22)
则
(23)
(24)
(25)
(26)
设角度β的正切值等于出射光两分量的振幅比,即
(27)
两分量间的相位差为
Δφ1=α2-α1
(28)
由于出射光光矢量轨迹应为一椭圆,设其长轴长度为B1,短轴长度为B2.设
(29)
根据文献[1],存在关系式
sin 2ε=sin 2βsin Δφ1
(30)
则可求得
(31)
由此可求得从第一波片出射的光矢量椭圆轨迹的离心率
(32)
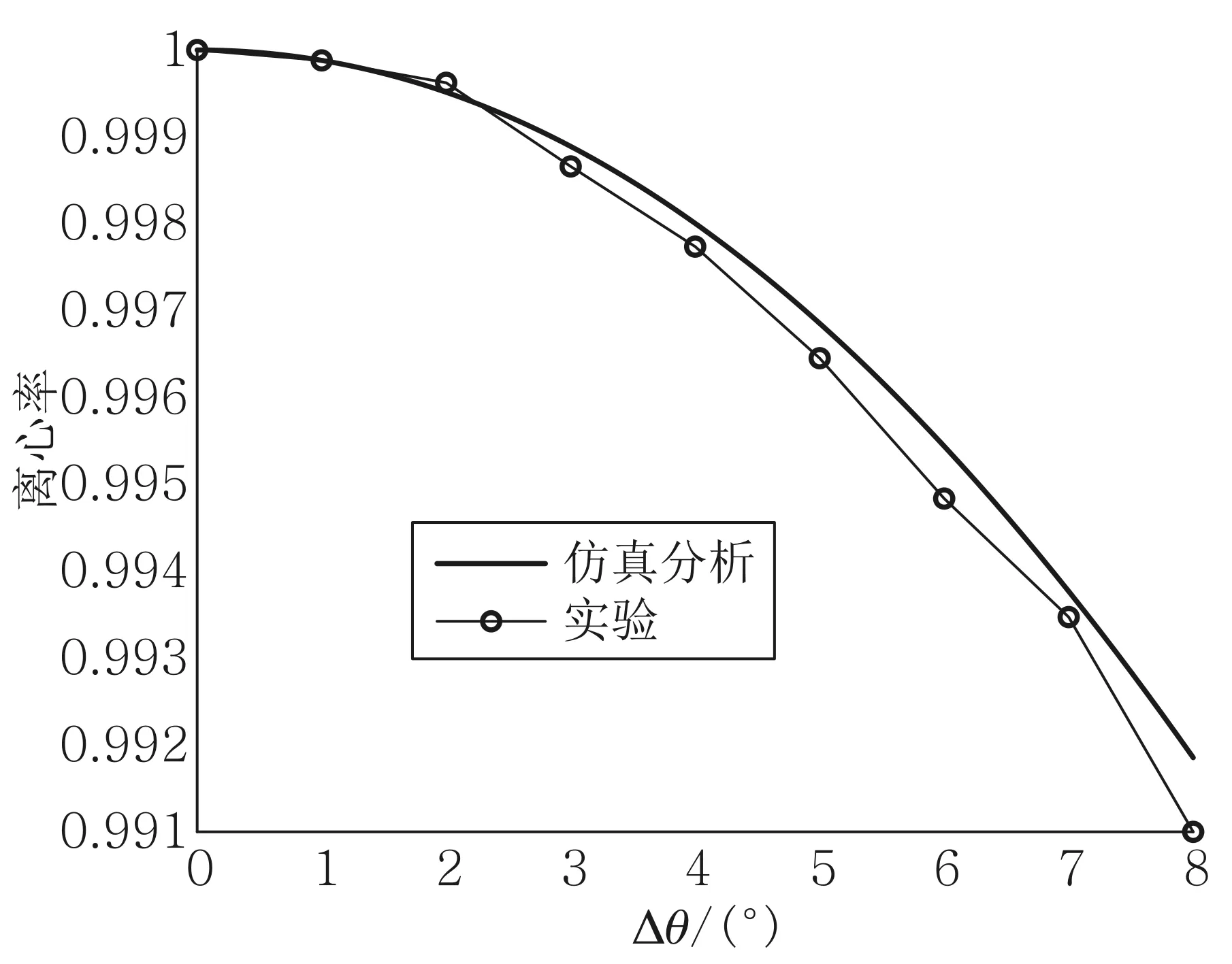
基于以上推导,利用MATLAB进行仿真得到了椭圆轨迹离心率与波片旋转角度误差间的关系曲线,见图1.在θ=±π/2时,获得曲线与θ=0时完全相同.由图1可见,在误差值为0时,离心率为1,意味着出射光为线偏振光.随着旋转角度误差逐渐增大,离心率有轻微下降.角度误差达到2°时,a=1/2、1/3、1/5的椭偏光入射,出射后其离心率仍在0.999以上;角度误差达到8°时,离心率均在0.991以上.可见,对于第一片1/4波片,出射光的偏振态对旋转角度误差敏感度很低,即使手动调整并不十分精确,出射光仍相当接近线偏振光.

图1 入射椭圆偏振光振幅比不同时,第一波片出射光矢量轨迹离心率与波片旋转角度偏差间的关系曲线
3.2第二片1/4波片的旋转角度误差对出射光偏振态的影响
由2.2节可知理论值θ=±π/4,首先考虑θ=π/4的情况,则第一波片出射的线偏振光通过该波片后,出射光偏振态为
(33)
同3.1节,有
(34)
两分量间的相位差为
(35)
(36)
由此可求得出射光椭圆轨迹的离心率
(37)
基于以上推导,利用MATLAB进行仿真得到了离心率与波片主轴方向角度误差间的关系曲线,见图2.在θ=-π/4时,曲线与θ=π/4时完全相同.由图2可见,当Δθ=0时,离心率为0,即轨迹是正圆形;随偏差角逐渐增大,离心率上升很快,偏差角到达2°时,离心率已接近0.4;偏差角到达8°时,离心率已接近0.7.可见对于第二片1/4波片,出射光的偏振态对旋转角度误差相当敏感,用手调整较难得到标准的圆偏振光.
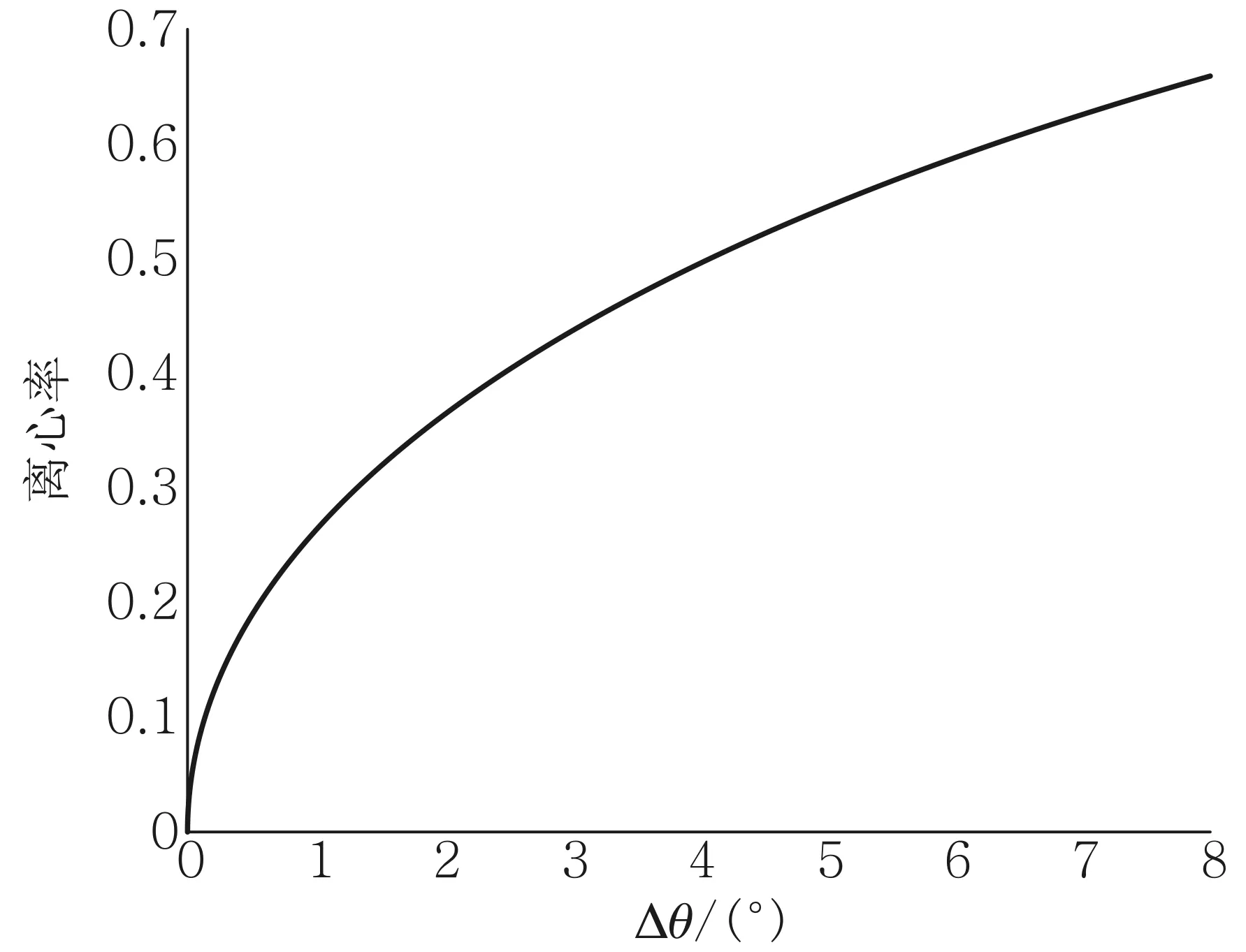
图2 光矢量轨迹离心率与第二波片旋转角度偏差间的关系曲线
4 椭圆偏振光转换为圆偏振光的实验设计
本实验主要验证利用一组级联波片将任意椭圆偏振光转换为圆偏振光的过程.实验装置的摆放如图3所示.图中从左到右依次为:光束准直器(与激光器相连)、约45°摆放的截止滤光片(用于产生椭圆偏振光),两个装有旋转架的1/4波片、带有二维调整架的光耦合器.光耦合器末端以光纤输出,连接偏振态分析仪.图4与图5分别为实验用1550 nm光源和PSGA-101-A偏振态分析仪.其中1550 nm光源输出的激光接近完全线偏振光,其偏振方向如图6,位于二、四象限,与纵轴夹角21.1°.

图3 实验主要装置

图4 1550 nm激光器

图5 偏振态分析仪

图6 光源输出激光偏振方向
实验步骤如下:
1) 在光学平台上隔一段距离安放光束准直器和光耦合器并调整其位置,使其基本对正.打开激光器,将光耦合器末端的光纤接到光功率计上.调整光耦合器的二维调整架,直至光功率计示数最大.此时将光纤与光功率计断开并连接至偏振态分析仪上.
2) 在准直器和耦合器中间放置一块截止滤光片,并使其与光路的光轴夹角约45°.截止滤光片为空间激光通信中常用器件,对某一波段光具有高反射率,而对另一波段光具有高透射率.从而可分开具有不同波长的发射光和接收光,使二者进入各自的发射和接收子光路系统中,因此其在实际系统中常采用与光轴成45°的摆放方式.此处利用截止滤光片来模拟空间光通信系统对偏振态的影响,从激光器出射的线偏振光在通过45°放置的截止滤光片时,由于光在薄膜表面倾斜入射,造成p光和s光之间具有一定相位差,使得线偏振光变为椭圆偏振光[5].观察偏振态分析仪,记录此时偏振轨迹,如图7(a).
3) 将一片1/4波片放置在截止滤光片与耦合器之间,转动波片同时观察偏振态分析仪,直至屏幕上的光矢量末端轨迹为一条直线,如图7(b).小心地转动波片,记录波片的旋转角度从0到8°(轨迹为直线时为0度)时的椭圆轨迹离心率,每次旋转的步进角为1°,共记录9个数据点.再次回到0度位置重复测量,共记录5组数据.记录多组数据取平均值可减小由于手动旋转波片导致的旋转角度误差.
4) 将第二片1/4波片放置在第一片波片与耦合器之间,转动第二块波片,直至分析仪屏幕上的光矢量末端轨迹为圆形,如图7(c).小心地转动波片,记录波片的旋转角度从0到8°(轨迹为圆时为0度)时的椭圆轨迹离心率,每次旋转的步进角为1°,共记录9个数据点.再次回到0度位置重复测量,共记录5组数据.
图7为实验过程中光束的偏振态变化.图7(a)为初始偏振态,椭圆短轴与长轴的比值1/5.在实验中值得注意的现象是,步骤3中,在旋转波片的环节很容易就能得到标准的线偏振光,而在步骤4中即使十分小心地转动波片,得到的最接近圆偏振光的结果仍与标准圆偏振光有着轻微的误差,如图7(c)所示.证明从椭圆偏振到线偏振,偏振态对旋转角度误差敏感度低,而从线偏振到圆偏振,偏振态对旋转角度误差敏感度很高,这与第3节的分析完全吻合.
图8给出了步骤3和步骤4中,偏振椭圆的离心率随波片偏转角度变化情况的理论值和实验值的对比.其中实线为根据第2节公式计算的仿真理论值,圆点线为实验得到的5组数据的平均值的连线.由于波片旋转角的精度较差(约为0.5°),理论值与实测值间存在少许误差,但整体趋势较为相符.此外从图8中还可看出,离心率越大(偏振态接近线偏振),理论值与实测值吻合越好;离心率越小(偏振态接近圆偏振),理论值与实测值差距越大.这也证明了,比起椭圆偏振到线偏振,波片放置的角度误差对线偏振到圆偏振的转换效果影响更大.

图7 实验中的光偏振态变化
第一波片

第二波片
5 结论
本文讨论了两种利用波片将椭圆偏振光转换为圆偏振光的方法,利用琼斯矩阵,由偏振态的转化结果(椭圆偏振—圆偏振、椭圆偏振—线偏振—圆偏振)反推出了波片应满足的条件,分析了使用双1/4波片情况下第一块或第二块波片分别存在旋转角度误差时对出射光偏振态的影响,并设计了实验进行验证,实验结果与理论分析吻合得很好.本文内容可以作为学生在学习光学中偏振部分时的拓展学习和实验内容,以加深学生对这部分知识的理解和掌握,并将所学内容与实际科研联系起来.
[1]郁道银,谈恒英. 工程光学[M]. 北京:机械工业出版社,2005:296,439-444.
[2]赵凯华,钟锡华. 光学[M]. 北京:北京大学出版社,2003:187-193.
[3]马磊,赵琨,李吉夏,等. 马吕斯定律用于退偏振片时的修正及实验验证[J]. 大学物理,2010,29(5):58-61.[4]杨鹏. 大气激光通信中圆偏振调制技术研究[D]. 北京:中国科学院大学,2012.
[5]陈卫斌. 投影显示系统偏振分析及偏振器件研究[D]. 杭州:浙江大学,2005.
Jones matrix analysis and experimental verification of conversion from elliptically polarized light to circularly polarized light
WANG Chao, JIANG Lun, DONG Ke-yan, AN Yan,JIANG Hui-lin
(NUERC of Space and Optoelectronics Technology; Fundamental Science on Space-Ground Laser Communication Technology Laboratory, Chang Chun University of Science and Technology, Changchun, Jilin 130022, China)
Using the Jones Matrix, we derive the parameters of the single wave plates or the double quarter-wave plates for converting the elliptically polarized light to circularly polarized light. To the double-wave-plate method, the influences of the rotating angle errors in the first or the second wave plates are quantitatively analyzed and validated through the experiment.
elliptically polarized light; circularly polarized light; Jones matrix; wave plate
2015-03-16;
2015-12-15
国家自然科学基金重大计划培育项目(91338116)、兵器预研支撑基金(62201070152)资助
王超(1986—),女,吉林长春人,长春理工大学讲师,博士,主要从事空间激光通信研究工作.
O 436.3
A
1000- 0712(2016)07- 0031- 06

