基于粒子滤波同化方法的实时洪水预报

杨瑞祥，梁　川，*，景　楠,杨来顺

( 1.四川大学 水利水电学院，成都 610065; 2. 水力学与山区河流开发保护国家重点实验室，成都 610065;3.三明水文水资源勘测分局，福建 三明 365000)



基于粒子滤波同化方法的实时洪水预报

杨瑞祥1，2，梁川1，2，*，景楠1，2,杨来顺3

( 1.四川大学 水利水电学院，成都 610065; 2. 水力学与山区河流开发保护国家重点实验室，成都 610065;3.三明水文水资源勘测分局，福建 三明 365000)

为了充分利用实时水文观测数据，提高预报的可靠性，将马斯京根分段连续流量演算法与粒子滤波同化方法进行耦合，构建了基于粒子滤波同化方法的实时洪水预报模型。采用沙溪干流的永安站至沙县站区间6场典型洪水过程对上述实时洪水预报模型进行了验证。结果表明，粒子滤波同化方法对马斯京根分段连续流量演算模型具有较好的适应性，由此得到的校正参数方案的确定性系数为0.85,与无实时校正结果方案和校正方案相比均有一定提高，且预报精度为甲级的洪水场次分别增加了2场和1场，使洪水预报精度得到了一定的提高。

马斯京根法；粒子滤波；实时洪水预报；数据同化

实时洪水预报能利用水情测报系统实时测量的水文数据，对原有洪水预报方案进行校正，以达到有效提高预报精度和防灾减灾决策水平的目的[1]。在实际工作中，常用的实时校正方法是最邻近误差校正法[2]和数据同化方法。后者能将观测数据融合到模型拟合结果中，对系统状态和参数不断进行更新，主要有变分方法和顺序同化方法。变分方法的代表是在气象领域常用的4D-Var算法[3]，顺序同化方法的代表是在水文领域得到应用的卡尔曼滤波及其优化算法[4]。但水文过程的非线性、非高斯特点使卡尔曼滤波的应用受到一定的限制。近年来得到进一步发展的粒子滤波算法适用于能用状态空间模型表示的非线性、非高斯系统，因此在水文领域的应用前景非常广阔。Moradkhani 等在评估水文模型参数和状态方面，应用粒子滤波算法并取得成功[5]。毕海芸等将粒子滤波算法应用于VIC模型中，对土壤水分进行估算[6]。徐兴亚等将粒子滤波算法与圣维南方程组结合，建立了河道洪水实时概率预报模型[7]。

本文在充分理解标准粒子滤波算法的基础上，将其与马斯京根分段连续流量演算模型进行耦合，建立实时洪水预报模型，并应用于福建省沙溪流域干流永安站至沙县站区间2002—2010年共6场典型洪水过程的检验及实时校正。

1　研究方法

粒子滤波同化方法是一种采用蒙特卡罗算法实现贝叶斯估计理论的算法，能够达到最优贝叶斯估计的效果[8]。其基本思想是利用从状态空间选取一组加权的随机样本粒子，来实现对状态的概率密度分布的逼近，然后用样本均值代替积分运算，以获得状态的最小方差估计。实际中一般采用序贯重要性采样方法来选取随机样本粒子。

1.1序贯重要性采样

序贯重要性采样是从采用的重要性密度函数中生成随机的粒子集合，利用最新的观测值递推更新得到当前的权值，将粒子归一化处理，再将每一个权值对应一个粒子，可得到相应的分布。

(1)

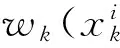
重要性密度函数q(xk|xk-1,z1：k)的选择会对粒子滤波的性能造成很大的影响，抑制退化问题的有效方法是选取好的重要性密度函数，从而减小需要的粒子数目，提高运行速度。常用的重要性函数有两种：①最优的重要性密度函数，性能更好但更难实现；②先验密度函数，虽然没有融入最新的观测值，但实现简单[9]。重要性密度函数:

(2)

式中p(xk|xk-1)为先验密度函数。

则粒子权值的表达式为:

(3)

式中p(xk|z1:k)为该时刻状态变量的后验概率分布。

(4)

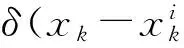
然而，上述方法的主要缺点是出现粒子匮乏现象。原因是在经过数次递推计算后，只有少数粒子的权值较大，其余粒子的权值太小以至于可忽略不计，选择任何重要性密度函数都会出现这种问题。因此，Gordan等[10]增加了重采样的步骤。

1.2重采样

重采样是在保持过程中粒子总数不变的情况下，从状态的后验概率密度中重新采样，将权重较小的粒子舍弃，保留或复制权重较大的粒子，将原来带权重的粒子集映射为新的等权重的粒子集。

通常采用粒子有效个数Neff来衡量粒子有效的数量[11]，近似为：

(5)

在序贯重要性采样时，如果Neff小于某个值，就应当进行重采样。

1.3算法实现

标准粒子滤波算法的基本公式是式(2)和式(3)[12]。实现步骤如下：

1)粒子权值更新。假设N个权值均等的预测粒子可近似表示t-1时刻状态变量的先验概率密度。在获得当前时刻的观测值zk-1后，重新计算每个粒子的权重。与观测值比较接近的粒子被赋予较大的权重，而与观测值相隔较远的粒子被赋予较小的权重，之后将粒子权重归一化。

2)粒子重采样。对粒子进行复制，权值越大则复制的次数越多，权值越小则复制的次数越少，权值过小的粒子直接被舍弃。经过重采样之后的粒子权重重新被均等地设置为1/N。

3)预测下一时刻状态变量。应用系统的状态转移方程对t时刻每个粒子的状态进行预测，得到t时刻的观测数据，据此更新粒子权重，具体做法同1)。

4)重复执行以上步骤，直到所有时刻运行完毕。

2　模型应用

2.1区域概况及洪水分析

永安(二)水文站与沙县(石桥)水文站两站间流域面积2 619 km2，河段全长78 km，洪水传播时间为6 h。本次共收集两站区间2002—2010年6场典型洪水过程，第4场洪水用作检验，其余5场洪水用作率定模型参数。原始资料观测时间间隔为1～5 h，为了达到预报要求，将其插值得到时间间隔为1 h的流量观测数据。经过分析可得，6场洪水中第5、6两场为双峰洪水，第5场洪水的第2个洪峰、第6场洪水的第1个洪峰峰现时间上游永安站不早于下游沙县站，且在同一场洪水中，2个洪峰相对大小相反。这些实际情况客观上造成预报较为困难。

2.2无实时校正方案

区间入流采用三水源新安江模型，模型参数率定结果见表1。

考虑河道平均传播时间作为预见期，取6 h，区间雨量站降雨过程及永安站入流过程由相关方案展延获得。

马斯京根分段连续演算法参数率定成果为：蓄量流量关系曲线的坡度K=6，流量比重系数x=0.4，时间间隔Δt=1h。则马斯京根分段连续流量演算法的参数Kl=Δt=1h，河段数n=6，x1=-0.1,计算得C0=0.375,C1=0.250,C2=0.375。

表1新安江模型(三水源)参数

Table 1Parameters of the Xinanjiang Model (3 components)

序号参数参数值序号参数参数值1WM1209IM0.452WUM1510SM50.453WLM8511EX1.154K0.3312KG0.115B0.5013KI0.796C0.2014F26197CI0.8815LAG58CG0.3316CS0.95

2.3实时校正方案

实时校正方案采用校正结果和校正参数两种方案进行比较，均实现了滚动预报。

2.3.1校正结果方案

校正结果方案是最直接的实时校正方案，通过最邻近误差校正方法实现。最邻近误差指的是与当前预报所依据的最邻近时刻的实测值与预报值之差，本文所依据的最邻近时刻与当前预报时刻之差就是预见期。校正后的预报值采用下式计算：

(6)

式中Qu,t+1为校正后的预报值；Qc,t+6为校正前的预报值；εt为最临近误差。

该法的优势是简便易行，便于预报人员根据实际情况具体操作，缺点是容易造成校正后的预报值发生剧烈振荡，且可能降低预报精度。

2.3.2校正参数方案

校正状态方案是通过粒子滤波方法，根据预报起始时刻到当前时刻的实测流量，优化模型的参数，据此向前预报。当有新的实测数据加入，则重新优化参数，继续滚动向前预报。该方案需要设定粒子数量、状态方差和观测方差3个参数。

粒子数量越多，计算效果理论上越好，但是计算时间增加。状态方差和观测方差越大，校正后的流量过程线偏离校正前的过程线的幅度越大，反之，则与校正前的过程线接近。经过多次率定，粒子数量取200，在保证一定精度的情况下不至于导致计算时间过长；该方案有两个变化的参数Kl和xl，因此状态方差取0.03和0.015，观测方差取100，使得能从流量过程线上看出有比较明显的校正，又不至于出现大的震荡现象。若采用校正参数C0、C1、C2的方法，反算回Kl、xl会发现取值很不合理，失去物理意义，因此不予采用。

2.4评价指标

根据《水文情报预报规范》(GB/T 22482-2008)[13]规定的洪水预报确定性系数和许可误差标准对上述3种方案进行评价。确定性系数DC按下式计算：

(7)

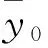
预报项目的精度按确定性系数的大小分为3个等级，精度等级按表2确定。

降雨径流预报以实测洪峰流量的15%作为洪峰预报许可误差；过程预报以90%的预报区间表示，精度指标选取观测值落入预报90%区间内的频率。

表2　预报项目精度等级

校正后模型效果DCt就是模型计算加上实时信息进行误差校正的总预报效果，校正效果DCu就是相对于原模型误差的效果[14]。效果定量评价系数分别为：

(8)

(9)

式中yci,u为实时信息进行误差校正的预报总流量。

3　效果评价

3.1预报结果

各场洪水预报流量过程线见图1，其中用作率定模型参数的是前5场洪水。

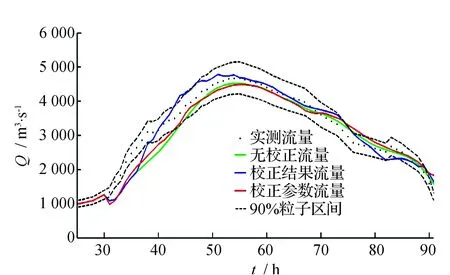
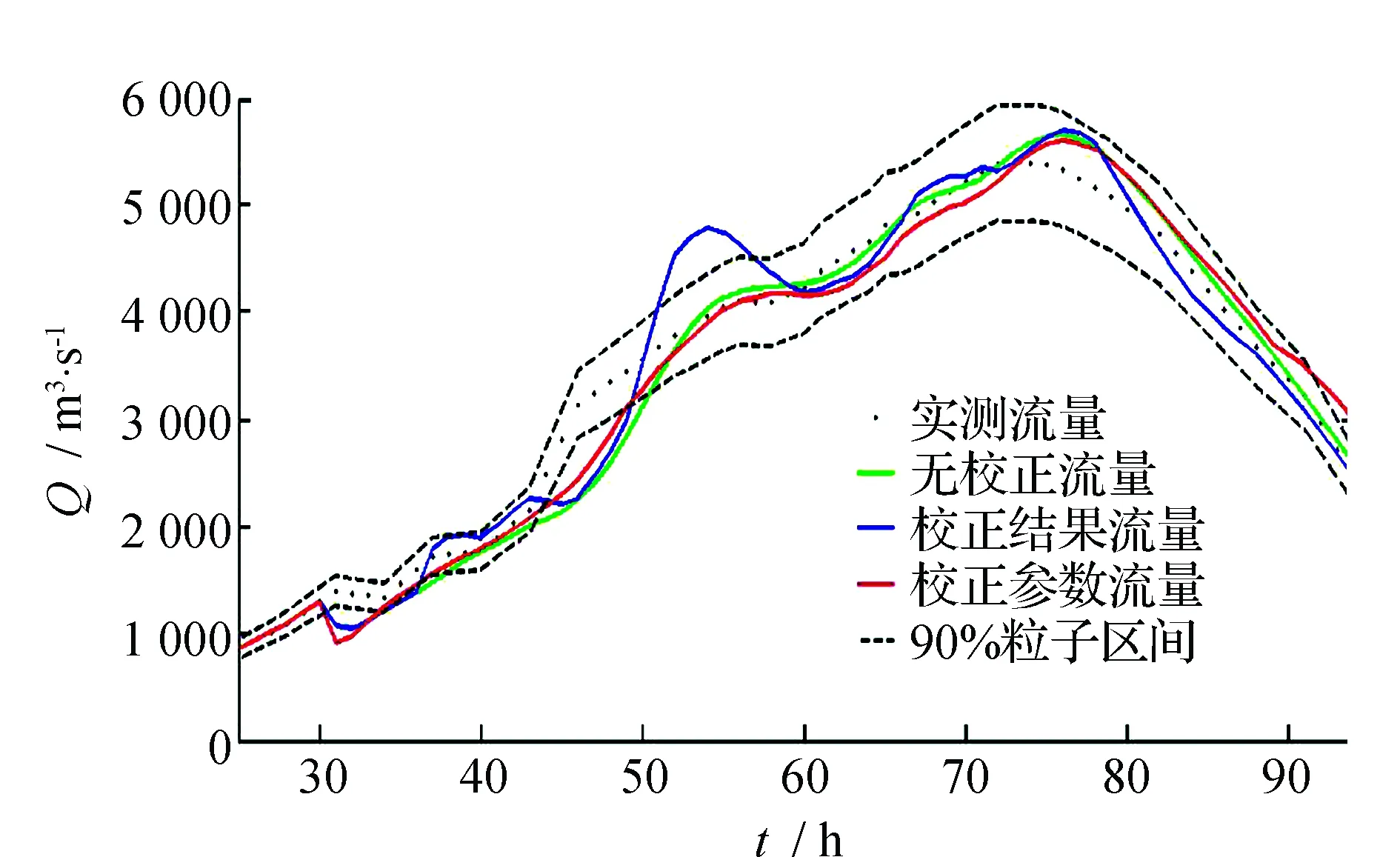
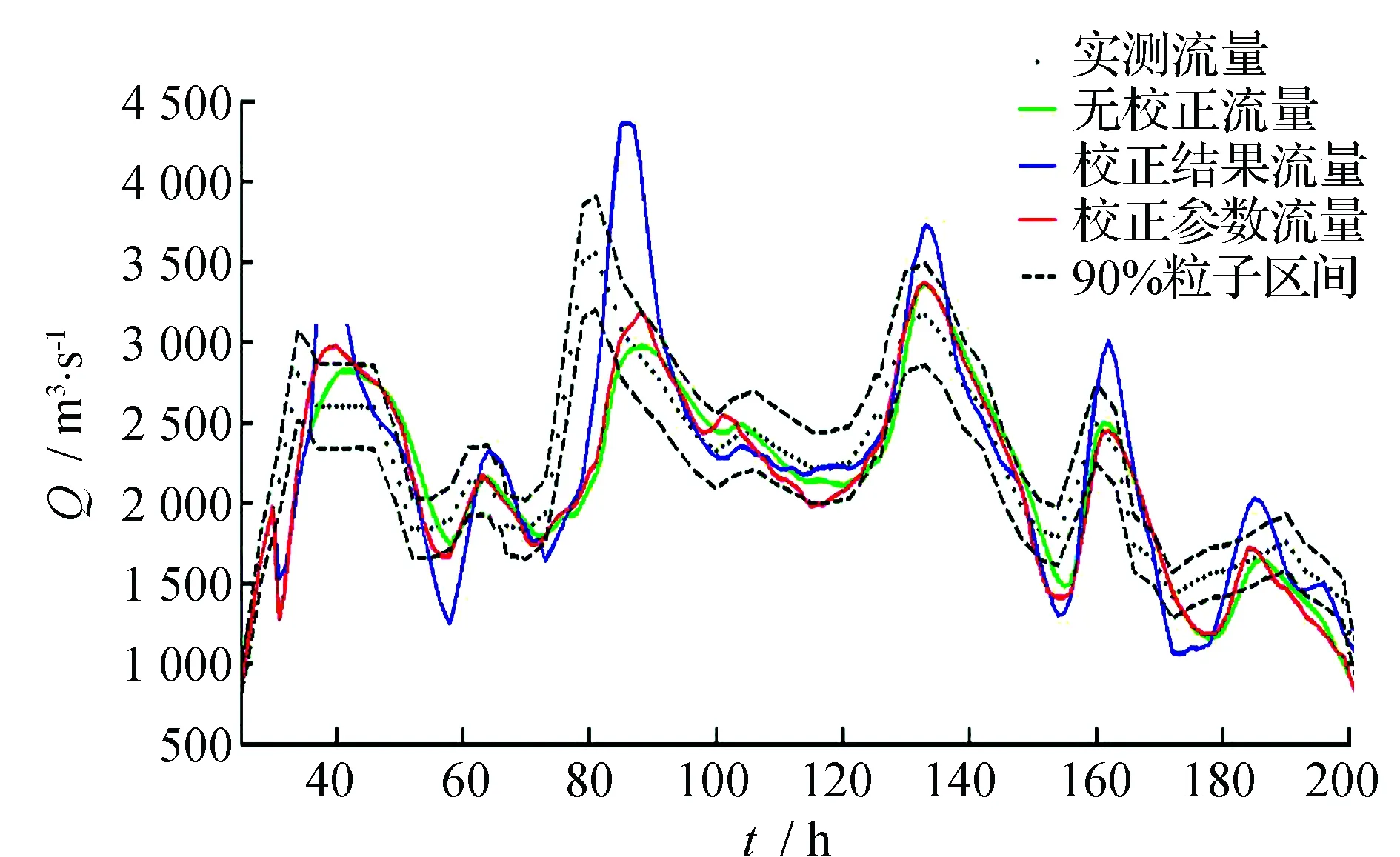
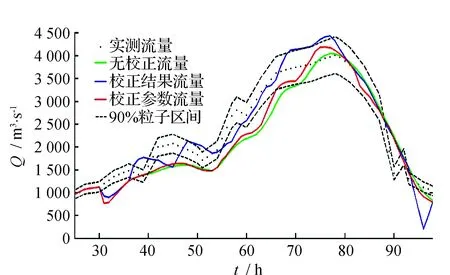
图1　沙县站洪水预报结果

由图1可见，从洪水过程线来看，校正结果方案得到的洪水过程线震荡较大，校正参数方案和无校正方案得到的洪水过程线较为接近，但前者与实测流量点据的配合较后者好。从洪峰流量和峰现时间上看，校正结果方案与实测值偏离最大，校正参数方案和无校正方案对于不同场次的洪水来说各有优劣。出现上述现象的原因是预报有6 h的预见期，如果在这6 h实测洪水过程线突然变陡或变缓，则会导致预报模型来不及响应，影响预报精度。

3.2结果评价

3种预报方案率定期、检验期和总的预报精度分别见表3、表4、表5。

表3　率定期洪水预报精度

表4　检验期洪水预报精度

表5　全部洪水的总预报精度

由表5可见，校正结果方案在确定性系数和洪峰合格率指标上均不如无校正方案，综合来看降低了无校正方案的精度。而相比于无校正方案，校正参数方案在各项评价指标上均有提高，说明粒子滤波同化方法的应用能够达到提高预报精度的目的。值得注意的是，预报值落在90%的区间内的频率仅有60%左右，说明过程预报精度有待进一步提高。

总之，本次预报效果从好到坏的排序是校正参数方案>无校正方案>校正结果方案。

4　结　论

1)首次提出粒子滤波同化方法与马斯京根分段连续流量演算法的耦合模型，该模型能够根据实时输入的实测流量值，校正预报误差，实现了对预报参数的时段动态更新，达到提高实时校正精度的目的。

2)以沙溪干流永安站至沙县站区间为例，根据流域典型洪水的资料，率定预报模型参数并采用校正结果和校正参数两种实时校正方案进行校正。计算结果表明，无校正方案的确定性系数为0.83，采用校正结果方案的确定性系数为0.81，采用校正参数方案的确定性系数为0.85，且预报精度为甲级的洪水场次较无校正方案增加了2场。说明所采用的粒子滤波同化方法的实时洪水预报模型能在一定程度上提高预报精度。

3)由于标准粒子滤波存在的粒子退化和重要性密度函数的选择问题，采用更有效的重采样算法和重要性密度函数是今后研究的重点。

[1]陆波. 流域水文模型与卡尔曼滤波耦合实时洪水预报研究[D].河海大学,2006.

[2]安全,范瑞琪,朱祯,等. 构建式流域实时水文预报系统关键技术研究[J]. 水文,2011(4):6-11.

[3]Dimet F X L, Talagr and O. Variational algorithms for analysis and assimilation o1 meteorological observations; theoretical aspects[J]. Tellus A,1986,38(2):97-110.

[4]王文,寇小华. 水文数据同化方法及遥感数据在水文数据同化中的应用进展[J]. 河海大学学报:自然科学版,2009(5):556-562.

[5]Moradkhani H, Hsu K-L, Gupta H, et al. Uncertainty assessment of hydrologic model states and parameters; sequential data assimilation using the particle filter[J]. Water Resources Research, 2004,41(5):W05012. doi: 10. 1029/2004WR003604.

[6]毕海芸,马建文,秦思娴,等. 基于残差重采样粒子滤波的土壤水分估算和水力参数同步优化[J]. 中国科学:地球科学,2014(5):1002-1016.

[7]徐兴亚,方红卫,张岳峰,等. 河道洪水实时概率预报模型与应用[J]. 水科学进展,2015(3):356-364.

[8]毕海芸,马建文. 粒子滤波算法在数据同化中的应用研究进展[J]. 遥感技术与应用,2014(5):701-710.

[9]魏国华. 粒子滤波算法研究与实现[D].北京：电子科技大学,2015.

[10] Gordon N J, Salmond D J, Smith A F M. Novel approach to nonlinear/non-gaussian bayesian state estimation[J]. IEEE Proceedings on Radar and Signal Processing, 1993,140(2):107-113.

[11] Bei Cao, Cai Wen Ma. A fine resampling algorithm for general particle filters[C]//4th International Congress on Image and Signal Processing,2011.

[12] 朱志宇.粒子滤波算法及其应用[M].北京:科学出版社,2010

[13] 中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.水文情报预报规范：GB/T 22482-2008[S].北京：中国标准出版社，2009.

[14] 包为民. 水文预报：第4版[M].北京:中国水利水电出版社,2009.

Real-time flood forecasting based on particle filter assimilation method

YANG Rui-Xiang1,2, LIANG Chuan1,2,*, JING Nan1,2, YANG Lai-Shun3

(1.CollegeofWaterResourceandHydropower,SichuanUniversity,Chengdu610065,China; 2.StateKeyLaboratoryofHydraulicsandMountainRiverEngineering,SichuanUniversity,Chengdu610065,China;3.HydrologicandWaterResourcesSurveyBureau,SanmingBranch，Sanming365000,Fujian，China)

To make full use of real-time hydrological data and improve reliability of forecasting, Muskingum piecewise continuous flow calculation model and particle filter assimilation method are coupled to build the real-time flood forecasting model based on particle filter data assimilation method. The above real-time flood forecasting model is verified by using interval six typical flood process from Yongan Station to Shaxian Station of Shaxi mainstream. The results show that the particle filter assimilation method has better adaptability to the Muskingum piecewise continuous flow calculation model. Based on this, the determined coefficient of the scheme of correcting parameter is 0.85. Compared with the scheme of non-real-time correction and correcting result, the determined coefficient is improved and the number of precision grade A of forecast are respectively increased by 2 and 1. The flood forecasting accuracy has been improved to some extent.

Muskingum method; particle filter; real-time flood forecasting; data assimilation

10.13524/j.2095-008x.2016.03.033

2016-07-29

国家自然科学基金资助项目(61006403)；水文学及水资源博士点基金资助项目(20130181110045)

杨瑞祥(1994-)，男，福建三明人，硕士研究生，研究方向: 水文水资源，E-mail: smsxfypy@qq.com; *通讯作者:梁川(1957-)，男，四川雅安人，教授，博士，博士研究生导师，研究方向: 水文水资源与水环境，E-mail: lshester@sohu.com。

P338

A

2095-008X(2016)03-0001-06