一种正交子空间投影高光谱图像端元提取算法

赵　岩,王东辉，张春晶，黄奕程，于明华

(1. 黑龙江科技大学 电气与控制工程学院，哈尔滨 150022；2. 哈尔滨工程大学 信息与通信工程学院，哈尔滨 150001；3. 齐齐哈尔车辆集团，黑龙江 齐齐哈尔 161000)



一种正交子空间投影高光谱图像端元提取算法

赵岩1,王东辉2，张春晶1，黄奕程3，于明华3

(1. 黑龙江科技大学 电气与控制工程学院，哈尔滨 150022；2. 哈尔滨工程大学 信息与通信工程学院，哈尔滨 150001；3. 齐齐哈尔车辆集团，黑龙江 齐齐哈尔 161000)

端元提取是高光谱图像混合像元分解的关键问题。针对正交子空间投影方法进行端元提取需要端元先验知识的问题，提出一种基于光谱最小信息熵的正交子空间投影高光谱图像端元提取方法。以光谱最小信息熵判定最优端元子集，同时将正交投影散度作为不同地物光谱向量之间相似性的测度指标用于判别端元。利用模拟数据和真实数据对算法进行验证，结果表明：算法不需先验知识，能够自动进行端元提取，且精度较高。

高光谱图像；正交子空间投影；端元提取；光谱最小信息熵；正交投影散度

高光谱图像以像元为单位获取地物信息，所记录的是像元内全部地物光谱的综合。由于空间分辨率的约束和地物的复杂多样性的影响，一个像元内经常包含有多种地物，称为混合像元(Mixed Pixel)[1-2]，作为分解基础的基本地物成分被称为端元(Endmember)[3]。为了更准确地描述真实地表的覆盖情况，需要对混合像元进行解混，计算出每一种地物成分在该像元中的所占比重。使用最广泛的的线性光谱解混(Linear spectral unmixing)是利用线性光谱混合模型(Linear Spectral Mixing Model, LSMM)把图像X中的每个混合像元分解成端元及其对应丰度，进而端元矩阵S和丰度矩阵A的过程[4]。端元提取的好坏是混合像元光谱分解效果的关键[6]。端元提取的主要算法有基于凸面几何学的Pixel Purity Index (PPI)、N-FINDR、Vertex Component Analysis (VCA)[7]，基于数学形态学的Automated Morphological Endmember Extraction (AMEE)，可以同时进行端元提取和丰度反演的Independent Component Correlation Algorithm (ICA)等。正交子空间投影算法(Orthogonal Subspace Projection, OSP)是在已知丰度分布的情况下根据信噪比最小推导出的，Harsanyi和Chang将OSP用于目标检测，通过信号光谱逐步提取出目标信号，但需要提供端元的先验知识[8-9]。在OSP的基础上，近年来研究者提出基于后验知识的信号空间正交投影(Signature Space orthogonal Projection, SSP)、目标空间正交投影(Target Signature space orthogonal Projection, TSP)及斜子空间投影(Oblique Subspace Projection, OBSP)[10]，这些方法都属于监督分解。通常情况下获取端元的先验知识是比较困难的。本文以光谱最小信息熵[11]判定最优端元子集，并利用正交投影散度作为相似性测度来判定端元，提出一种非监督的改进正交子空间投影方法(Improved Orthogonal Subspace Projection, IOSP)，用以自动提取端元。

1　正交子空间投影端元提取算法

设X为L×1维的像元光谱向量，S=[s1,s2,…,sp]为L×P维的端元光谱矩阵，A=[a1,a2,…,ap]T是P维向量，其中ai为对应端元的丰度，N为L×1维的随机噪声。像元的线性光谱混合模型表示为:

X=SA+N

(1)

(2)

(3)

OSP端元提取的步骤：

1) 根据凸面几何学理论，通常认为端元位于特征空间的角点上，即所谓最大光谱向量法。满足式(4)，得到一个待选端元，它是图像中亮度最大的像元。

(4)

2) 判断待选端元是否为噪声，如果是噪声，除去；如果不是噪声，则为端元。

3) 消除已经提取端元在图像中的影响，生成新的图像数据。

OSP认为像元是由目标信号d和背景端元U两部分组成。设d=si,1≤i≤P，则背景端元向量空间U=(s1…si-1si+1,…,sp)。因此，式(4)可以写为:

(5)

式中ai为si的丰度；b=(a1…ai-1ai+1…ap)T为对应背景端元的丰度向量。

通过正交子空间投影算子U⊥对背景及噪声进行抑制，由最小二乘估计得到U⊥=I-UU#，其中，式中⊥为正交补空间，#为Moore-Penrose广义伪逆矩阵，U#=(UTU)-1UT，-1为矩阵逆运算，I为P×P维的单位阵。在假设噪声与信号不相关的条件下，提取信号d的算子为：

(6)

其中，λ=(dTU⊥d)-1为一个表示分解精度的常数项[12]。

从式(6)可知，OSP算法在进行端元提取时，需要图像端元的先验知识。

4) 判断是否满足结束条件(已提取的端元数达到指定的数目)，若满足，则结束计算；若不满足，则循环步骤1)～3)。

2　改进的正交子空间投影端元提取算法

2.1光谱最小信息熵

光谱最小信息熵(SMSE)算法利用高斯分布概率函数得到高光谱图像像元光谱的概率，用来计算光谱的信息熵，之后通过设置阈值筛选出小于阈值的信息熵的光谱，并累加光谱曲线概率，经过运算获得端元。 SMSE算法如下式：

(7)

其中，

式中xi为(j,k)像元在第i个波段的灰度值;μi和σi为第i个波段灰度值的均值和方差;P(j,k)为光谱曲线概率;a为常数。

2.2基于正交投影散度的端元判定

正交投影散度(orthogonal projection divergence, OPD)来源于OSP的原理[13]，其目的是最大程度地分离目标信息和背景噪声信息，计算得到的正交投影后的残差，作为衡量不同地物光谱向量之间相似性大小的指标。

考虑两个M维光谱信号ri=[ri1,ri2,…,riM]T，rj=[rj1,rj2,…,rjM]T，则ri和rj之间的OPD为：

(8)

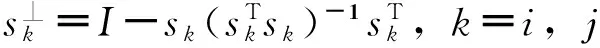
IOSP端元提取的步骤：

1) 按SMSE算法计算获得待选端元。

2) 按基于正交投影散度的端元判定法判断待选端元是否为噪声，如果是噪声，做出标记，排除；如果不是噪声，则为端元。

3) 基于正交投影散度的端元判定法获得1个端元信号d=s1，利用d的正交补空间d⊥消除端元的d=s1影响，其中d⊥=I-d(dTd)-1dT。将d⊥作用于OSP模型中，d⊥X=d⊥Ub+d⊥N，噪声有效地压制为d⊥N。

将d⊥X作为新的图像数据，提取端元e2，获得d=[e1,e2]，循环运算，直至提取P个端元。

3　仿真实验

3.1性能指标

采用光谱角度距离(Spectral Angle Distance, SAD)作为指标进行精度评价。

对于第i个端元，SAD定义为：

(9)

图1　Alunite, Buddingtonite, Chalcedony, Kaolinite的光谱Fig.1　Reflectances of Alunite, Buddingtonite, Chalcedony, Kaolinite

3.2模拟数据实验

从USGS矿物光谱库中选取4种相互之间线性独立的端元光谱(Alunite, Buddingtonite, Chalcedony, Kaolinite)，见图1。反射率的波长为0.38～2.5 μm，按照Dirichlet分布进行混合，先对端元丰度之和进行归一化，然后加上不同的高斯白噪声，波段数是224，图像大小是256×256像元，形成模拟实验数据。

抗噪性能实验：在混合光谱中加入随机噪声。

(10)

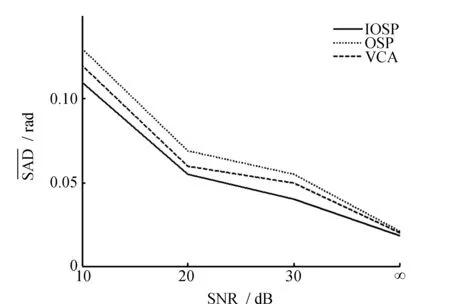
图2　噪声强度不同下算法性能的比较Fig.2　Comparison of Algorithm performance of different oise intensity

图3　Nevada州Cuprite地区的AVIRIS图像(193波段)Fig. 3　AVIRIS image data in cuprite region (193 band)

3.3真实数据实验

采用美国Cuprite Nevada地区的AVIRIS高光谱数据(图像大小400×350像元，波长为1.99～2.48 μm，于1995年成像)，172～221波段间的共50个波段数据，见图3。去掉大气吸收的221波段，实际采用49个波段进行实验，图像大小为13.3 MB。

IOSP、VCA、OSP算法所输出Cuprite地区5种常见矿物端元与相应实际地物参考光谱的相似度见表1。采用虚拟维度(VD)方法[14]获得的图像端元数目。可见，IOSP考虑端元光谱相关性影响，进一步提高了提取端元的纯度，表现较为稳定。

表1　3种算法的SAD比较

4　结　论

本文在研究OSP算法的基础上，以光谱最小信息熵判定最优端元子集，将正交投影散度用于不同地物光谱向量之间相似性的测度，利用正交投影散度均值判定候选端元是端元，还是噪声，逐个获得高光谱图像中的所有端元。笔者提出的IOSP算法克服了OSP需要先验知识的不足，通过模拟、真实数据实验分析，表明IOSP算法能够自动进行端元提取，且提取结果较好。

[1]Thouvenin P A, Dobigeon N, Tourneret J Y. Hyperspectral unmixing with spectral variability using a perturbed linear mixing model[J]. IEEE Transactions on Signal Processing, 2016, 64(2):525-538.

[2]Lin C H, Chi C Y, Wang Y H, et al. A fast hyperplane-based minimum-volume enclosing simplex algorithm for blind hyperspectral unmixing[J]. IEEE Transactions on Signal Processing, 2016, 64(8):1946-1961.

[3]杜培军, 谭琨, 夏俊士. 高光谱遥感影像分类与支持向量机应用研究[M]. 北京: 科学出版社, 2012: 130.

[4]张兵, 高连如. 高光谱图像分类与目标识别[M]. 北京: 科学出版社, 2011: 112.

[5]刘国华.基于图像处理的钻头测量系统[J].黑龙江大学工程学报，2016，7(1)：92-96.

[6]王立国, 赵春晖. 高光谱图像处理技术[M]. 北京: 国防工业出版社, 2013: 11.

[7]Chang C I, Chen S Y, Li H C, et al. Comparative study and analysis among ATGP, VCA, and SGA for finding endmembers in hyperspectral umagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2016:1-27.

[8]Harsanyi J C, Chang C I. Hyperspectral image classification and dimensionality reduction: an orthogonal subspace projection approach[J]. IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(4): 779-785.

[9]Chang C I. Further results on relationship between spectral unmixing and subspace projection[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 1030-1032.

[10] Tu T M, Chen C H, Chang C I. A posteriori least squares orthogonal subspace projection approach to desired signature extraction and detection[J]. IEEE Transactions on Geoscience and Remote Sensing, 1997, 35(1):127-139.

[11] 杨可明, 刘士文, 王林伟,等. 光谱最小信息熵的高光谱影像端元提取算法[J]. 光谱学与光谱分析, 2014(8):2229-2233.

[12] Chang C I, Zhao X L, Mark L G, et al. Least squares subspace projection spproach to mixed pixel classification for hyperspectral images[J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 898-912.

[13] Keshava N. Distance metrics and band selection in hyperspectral processing with applications to material identification and spectral libraries[J]. IEEE Trans. Geoscience Remote Sensing, 2004, 42(7): 1552-1565.

[14] Chang C I, Du Q. Estimation of number of spectrally distinct signal sources in hyperspectral imagery[J]. IEEE Transactions on Geoscienee and Remote Sensing, 2004, 42(3): 608-619.

An Orthogonal Subspace Projection for endmember extraction algorithm in hyperspectral images

ZHAO Yan1，WANG Dong-Hui2，ZHANG Chun-Jing1，HUANG Yi-Cheng3，YU Ming-Hua3

(1.SchoolofElectricalandControlEngineering,HeilongjiangUniversityofScienceandTechnology,Harbin150022,China;2.CollegeofInformationandCommunicationEngineering,HarbinEngineeringUniversity,Harbin150001,China;3.QiqiharVehicleGroup,Qiqihar161000,Heilongjiang,China)

Endmember extraction is the key problem of hyperspectral images mixed pixel decomposition. To address Orthogonal Subspace Projection method for endmember extraction needing to solve the problem of endmember prior knowledge, a hyperspectral image endmember extraction method of Orthogonal Subspace Projection based on spectral minimum shannon entropy was proposed. It determined the optimal endmembers subset using the criteria of spectral minimum shannon entropy, and the Orthogonal Projection Divergence as a measure index of similarity between different spectral vector for judging the endmember. The algorithm was verified by the simulated hyperspectral images and real hyperspectral images. Experimental results show that the proposed algorithm can extract endmember automatically without prior knowledge and achieve relatively high extraction accuracy.

hyperspectral images; Orthogonal Subspace Projection(OSP); endmember extraction; Spectral Minimum Shannon Entropy(SMSE); Orthogonal Projection Divergence(OPD)

10.13524/j.2095-008x.2016.03.046

2016-07-30

黑龙江省教育厅科学技术研究项目(12541734)；国家自然科学基金资助项目(61275010)

赵岩(1976-)，女，黑龙江齐齐哈尔人，讲师，博士研究生，研究方向：图像处理、智能控制，E-mail:zh_ao_yan@sina.com。

TP751

A

2095-008X(2016)03-0082-05