基于LabVIEW与Matlab的气动位置系统模型辨识及分析

朱正龙，汤茂银，孔　丽，汪玉兰

（1.遵义师范学院工学院，贵州遵义563002；2.湖南机电职业技术学院汽车工程学院，湖南长沙410000）

基于LabVIEW与Matlab的气动位置系统模型辨识及分析

朱正龙1，汤茂银2，孔丽1，汪玉兰1

（1.遵义师范学院工学院，贵州遵义563002；2.湖南机电职业技术学院汽车工程学院，湖南长沙410000）

复杂系统数学模型的建立，采用传统的计算方法需要对整个系统的每个子系统进行详细的分析计算，往往需要耗费大量的时间；作者利用LabVIEW与Matlab系统辨识工具箱对气动位置闭环控制系统进行模型参数辨识，得到复杂系统的数据模型，大大节省了系统数学模型建立的时间；作者对所建立的模型进行阶跃响应特性分析，从曲线可以看出辨识的模型能较好地实现阶跃响应，说明此方法建立的模型是有效的。

LabVIEW；模型辨识；气动位置系统

气动位置闭环控制系统在自动化生产线、工业机器人等领域运用非常广泛。在实际运用中，通常需要高精度的精准控制，必须建立各个子系统的准确数学模型。对于一个完整的气动控制系统，使用传统的方法建立整个系统的数学模型是一项非常复杂、繁琐和费时的工作。基于此，本文利用LabVIEW与 Matlab系统辨识工具箱对气动位置闭环控制系统进行模型参数辨识，大大节省了系统数学模型建立的时间，并对所建立的模型进行阶跃响应特性分析，从曲线可以看出辨识的模型能较好地实现阶跃响应，说明此方法建立的模型是有效的。

1　气动位置系统数据采集与处理

气动位置控制数据采集系统主要由无杆气缸、电比例阀、采集卡、模拟式位置传感器和计算机等组成，如图1所示。

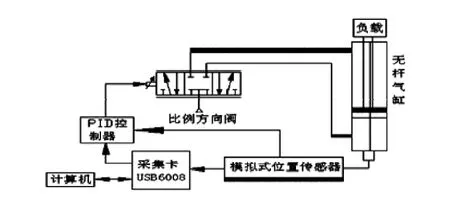
图1　为气动位置控制系统原理图

控制过程：将给定值与反馈值输入控制器，控制器控制比例阀，比例阀控制无杆气缸。同时给定值与反馈值经过数据采集卡输入计算机进行存储分析。

1.1气动位置系统数据采集

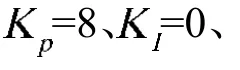
图2　系统数据采集硬件接线图

本文采集了1000组数据：［1.525376 2 1.525376 2 1.525376 2…1.617052 2 3.094054 4］，图3为1000组数据中的一段输入与反馈数据图示，图4为数据采集显示与存储程序。程序中选用波形图标对数据进行显示，用测量文件（LVM）对数据进行存储，以便随时对数据进行调用分析。

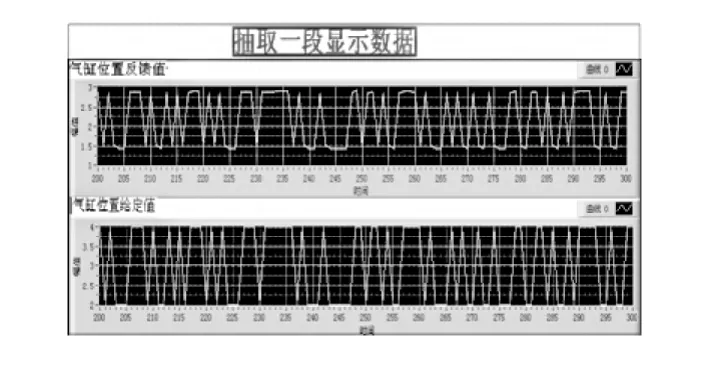
图3　M序列激励信号气缸位置显示

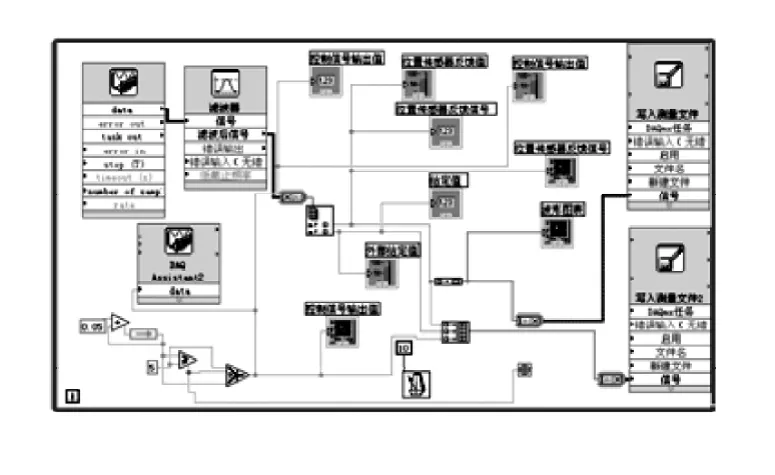
图4　数据采集显示与存储程序

2　气动位置控制系统模型辨识和特性分析

2.1系统辨识的基本原理

系统模型辨识是基于输入与反馈数据的基础上，从一组模型数据中，确定一个与研究系统等价的数学模型。

2.2最小二乘法ARX模型辨识基本原理

本文选用MATLAB中的ARX（AutoRegressive eXogenous）模型来对模型进行辨识，先假设所研究的模型具有ARX结构。ARX模型结构可表示为：

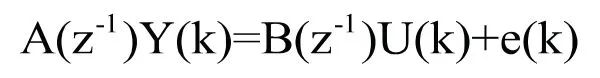
2.3ARX模型辨识在MATLAB中的实现

在MATLAB中，系统辨识工具箱经过数据预处理、模型结构辨识、模型参数辨识与模型验证来完成模型的建立；通过多个函数的组合完成数据的预处理，再进行模型结构辨识，即根据实验对研究对象进行特性假设；模型类确定后，根据采集的输入与响应数据，确定模型结构参数，再进行验证，以检验模型的可靠性。

2.4ARX模型的气动位置系统模型辨识

2.4.1数据预处理

本文研究的是闭环气动位置系统，用来完成系统辨识的数据为一组单输入单输出数据，共81组数据。数据的输入由程序内部激励电压产生，输出的数据为无杆气缸上模拟式位置传感器的电压信号。为了消除数据中的线型或缓慢变化数据，需要对数据进行预处理。设定u（k）为激励电压，y（k）为模拟式位置传感器测量的无杆气缸实际位置反馈值的响应信号。

u为81个电压采样输入值，y为81个无杆气缸位置反馈值，采样频率为100Hz。MATLAB的系统辨识工具箱数据处理采用iddata进行，而u、y都是一维的向量，因此需要将u、y转化为iddata对象，Data=iddata（y，u，0.01），Data对象包含了所研究系统的输入与响应参数。

Data=［1.525376 2 1.525376 2 1.525376 2…1.617052 2 3.094054 4］；导入81组据；

u=data（2：2：162）；%81组气缸位置输入值；

y=data（1：2：161）；%气缸反馈值，即系统输出值；

u=u’；

y=y’；%将输入输出向量转化为列向量形式，以满足iddata函数式要求；

Data=iddata（y，u）；%生成包含输入、输出数据的iddata对象；

plot（Data）；%显示输入输出数据曲线，如图5所示；

position=iddata（y，u）；

position.InputName='电压'；%激励电压；

position.OutputName='气缸位置'；%气缸实际位置表示；

position=iddata（y，u）；%重新生成包含输入、输出数据的iddata对象；

position=detrend（position）；%数据预处理；

Datai=position（1：40）；%取数据前半部分；

Datav=position（40：81）；%取数据后半部分；

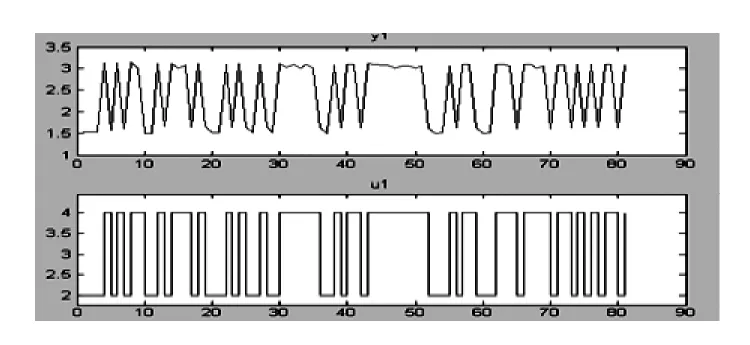
图5　原始数据曲线

采用MATLAB系统辨识工具箱的drend函数来对数据进行处理，以消除数据的趋势项，把测量的数据变成均值为零。数据预处理结果如图6所示。

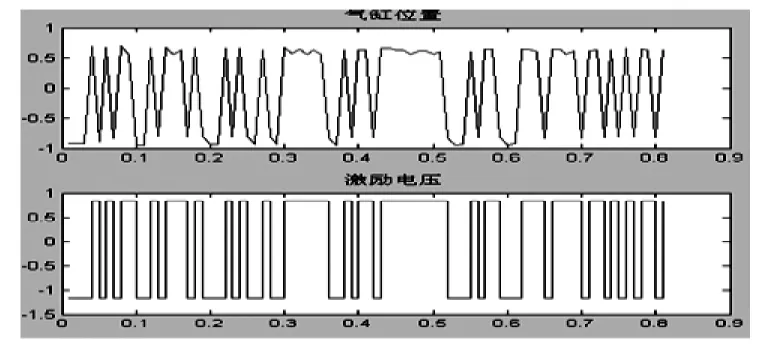
图6　加预处理后的数据曲线

从图6可看出，经过预处理后的数据消除了数据中的趋势项，得到了比较理想的曲线。

2.4.2确定模型结构类型和阶次

MATLAB辨识工具箱调用ARX模型参数格式的形式为：M=ARX（DATA，ORDERS）其中，ORDERS=［na nb nk］为模型阶次向量，DATA为研究系统模型辨识的输入与响应数据。模型结构函数为selstruc，AIC极小化模型函数为：nn=selstruc（v，‘aic’），其中，v为模型损失函数。要求出模型的阶次需要得到模型结构的损失函数，计算多个单ARX模型损失函数的函数为arxstruc，调用格：V=arxstruc（Data，Data，NN）；其中，第1个Data为模型辨识的输入、输出数据向量或矩阵；第2个Data为验证的输入、输出数据向量或矩阵；NN模型结构参数矩阵，NN每一行的形式为：nun=［an nab no］。

程序代码为：

V=rostrum（Datai，Datav，struc（1：10，1：10，1：10））；%计算多个单ARX模型的损失函数；

nn=selstruc（V）；%确定模型参数结构；

根据气动位置控制系统的特性，选择组合nn=［5 5 1］。

2.4.3确定模型参数与模型验证

在MATLAB中，调用ARX函数进行模型参数验证，程序如下：

M=arx（Data，［5 5 1］）；%确定ARX模型参数

运行的模型结果：

Discrete-timeIDPOLYmodel：A（q）y（t）=B（q）u（t）+e（t）

A（q）=1+0.7175q^-1+1.825q^-2+2.432q^-3+0.3724 q^-4+2.09q^-5

B（q）=0.4743q^-1+1.313q^-2+1.829q^-3+0.2387 q^-4+1.616q^-5

由此得到模型的传递函数为：

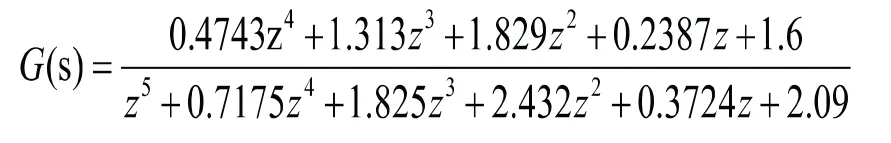
得到模型以后，对ARX模型的有效性进行验证。用一组去除趋势项的输入与响应数据对模型进行验证，比较模型输入与系统实际反馈值之间的误差，从图7可以看出，模型输出曲线和实际曲线重合较好。

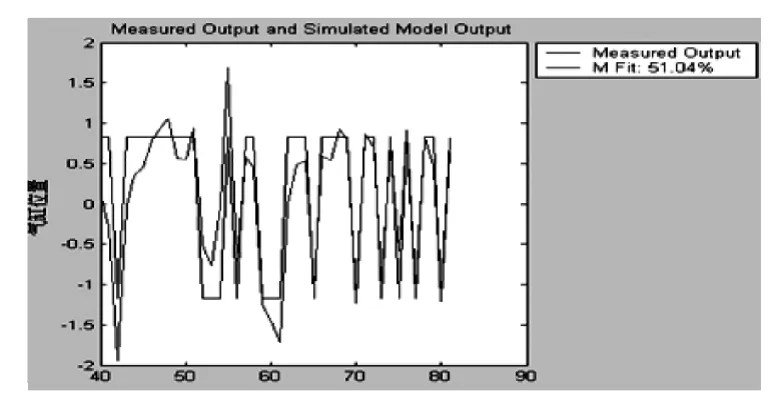
图7　模型输出曲线和实际曲线

2.5模型特性分析及参数整定

2.5.1模型处理

经过辨识得到离散闭环传递函数模型，为了对气动位置控制系统进行特性分析，需要去除闭环模型离散环节，并进行连续化处理。根据气动位置系统的特征，先将其降为三阶的模型系统，再对模型进行特性分析，最后得到连续的三阶数学模型：

2.5.2特性分析及参数整定

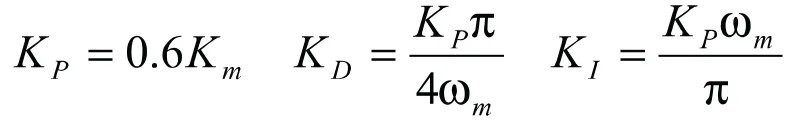
由此得到系统的传递函数为：

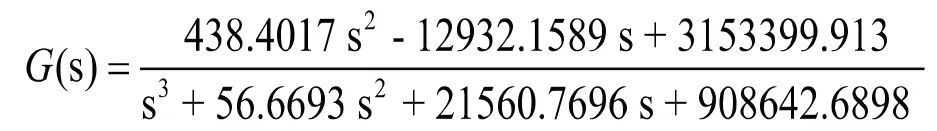
应用Ziegler-Nichols方法求PID三个参数，阶跃响应曲线如图8所示。进而求出参数，Km=0.25744，Wm=128.47，Km=0.19334，Kd=0.012522，Ki=7.4628。从图9ID闭环系统阶跃响应曲线可以看出，当系统引入PID控制后，气动系统能较好地实现阶跃响应，从而说明所建立的模型是有效的。

图8　PID控制前后阶跃响应图

3　结语

本文采用LabVIEW与Matlab对气动位置闭环控制系统进行数据采集存储分析，采用基于最小二乘法的ARX方法对其进行模型辨识，最后对所建立的数学模型进行阶跃响应分析，结果证明所建立的模型是有效的。

［1］刘宪林，杜晓勇，田云峰，等.Matlab在水轮机模型辨识中的应用［J］.电力自动化设备，2007，（12）：85-87.

［2］齐晓慧，田庆民，董海瑞.基于Matlab系统辨识工具箱的系统建模［J］.兵工自动化，2006，（10）：88-90.

［3］孙书立，胡守印.MATLAB在热工系统辨识中的应用［J］.科学技术与工程，2005，（5）：309-312.

［4］刘明月.水箱液位系统的RBF-ARX模型与预测控制的研究［D］.长沙：中南大学，2014.

［5］董玲，曾佳，杨晶晶，等.基于LabVIEW和Matlab混合编程的在线信号与线性系统实验［J］.实验室研究与探索，2014，（12）：113-116.

［6］徐晓峰，朱德森.基于DSP的伺服控制系统设计［J］.工业控制计算机，2003，（5）：26-27.

［7］姚巍.自行车机器人系统辨识及MATLAB仿真［D］.北京：北京邮电大学，2008.

［8］戴敬，王世立.LabVIEW基础教程［M］.北京：国防工业出版社，2002.3-20，157-164.

［9］马建明.数据采集与处理技术［M］.西安：西安交通大学出版社，1998.50-78.

（责任编辑：朱彬）

On the Cognition and Analysis of Pneumatic Position System Model based on LabVIEW and Matlab

ZHU Zheng-long1，TANG Mao-yin2，KONG Li2，WANG Yu-lan1
（1.Engineering College，Zunyi Normal College，Zunyi 563002，China；2.School of Automotive Engineering，Hunan Mechanical&Electrical Polytechnic，Changsha 410000，China）

The establishment of complex system model for math needs to adopt traditional calculating method to make a detailed study of the every sub-system of the whole system，which must take much time；LabVIEW and Matlab are used to make an identification of pneumatic position closed-loop control system in terms ofparameter model，and a complex systematic data model is attained，which saves much time to set up systematic math model；a step-response analysis is made of the features of the established model；and from the curve，we can see that the identified model can better serve the function of step response，proving that this method is effective.

LabVIEW；model identification；pneumatic position system

TP273

A

1009-3583（2016）-0106-04

2015-12-04

贵州省科学技术联合基金项目（黔科合LH字［2015］7045号）

朱正龙，男，贵州遵义人，遵义师范学院工学院工程师，硕士，主要从事流体传动与控制的科研和教学工作。